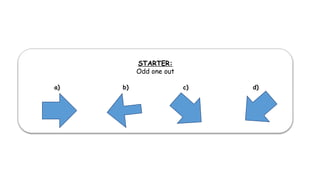
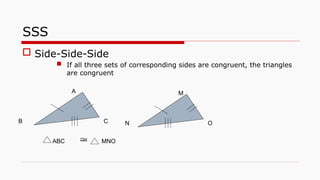
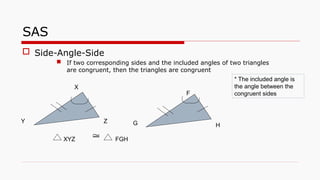
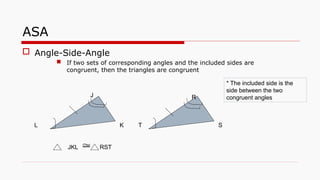
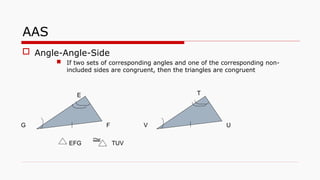
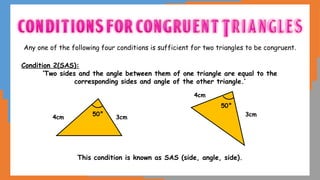
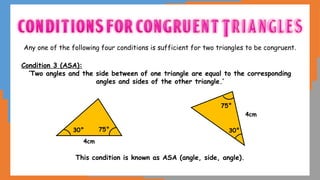
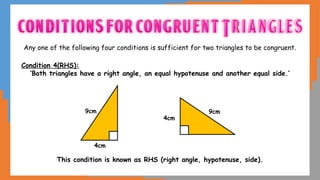
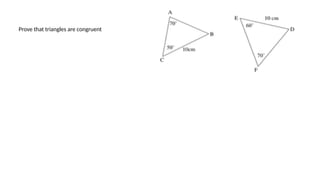
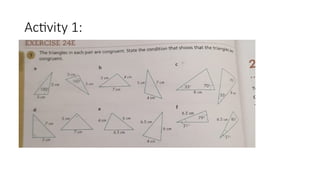
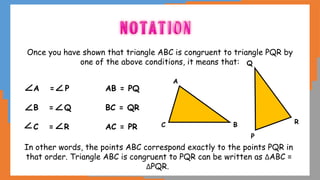
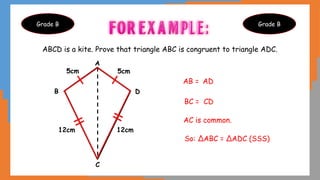
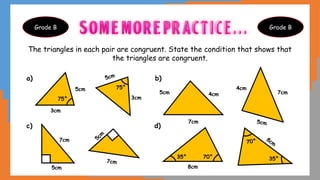
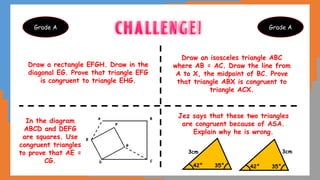
This document outlines the concept of congruency in triangles, detailing four key conditions under which triangles can be considered congruent: SSS (side-side-side), SAS (side-angle-side), ASA (angle-side-angle), and RHS (right angle-hypotenuse-side). It provides examples and activities to illustrate these conditions and their applications in proving triangles' congruency. Additionally, it includes exercises for students to practice identifying congruent triangles and applying the rules discussed.

1. Chapter 24
Geometrical terms and
relationships

2. STARTER:
Odd one out
a) b) c) d)

3. Objectives
Find out the congruence rule
Check two triangles are congruent
Congruent Triangles.
Keywords:
Congruency
Triangles

4. Introduction

5. Two shapes are congruent if they are exactly the same size and shape.
For example, these triangles are all congruent.
Notice that the triangles can be differently oriented (reflected or rotated).

6. SSS
 Side-Side-Side
 If all three sets of corresponding sides are congruent, the triangles
are congruent
ABC MNO

A M
O
N
C
B

7. SAS
 Side-Angle-Side
 If two corresponding sides and the included angles of two triangles
are congruent, then the triangles are congruent
XYZ FGH

X
Y Z
F
G H
* The included angle is
the angle between the
congruent sides

8. ASA
 Angle-Side-Angle
 If two sets of corresponding angles and the included sides are
congruent, then the triangles are congruent
JKL RST

J
L K T
R
S
* The included side is the
side between the two
congruent angles

9. AAS
 Angle-Angle-Side
 If two sets of corresponding angles and one of the corresponding non-
included sides are congruent, then the triangles are congruent

EFG TUV
E
G F
T
V U

10. HL
 Hypotenuse-Leg
 If the hypotenuse and one set of corresponding legs of two right triangles
are congruent, then the triangles are congruent

CDH RAM
A
D H
R
C
M

11. Any one of the following four conditions is sufficient for two triangles to be congruent.
Condition 1(SSS):
‘All three sides of one triangle are equal to the corresponding sides of the other
triangle.’
2.4cm 2.2cm
3cm
3cm
2.4cm
2.2cm
This condition is known as SSS (side, side, side).

12. Any one of the following four conditions is sufficient for two triangles to be congruent.
Condition 2(SAS):
‘Two sides and the angle between them of one triangle are equal to the
corresponding sides and angle of the other triangle.’
This condition is known as SAS (side, angle, side).
4cm 3cm 3cm
4cm
50°
50°

13. Any one of the following four conditions is sufficient for two triangles to be congruent.
Condition 3 (ASA):
‘Two angles and the side between of one triangle are equal to the corresponding
angles and sides of the other triangle.’
This condition is known as ASA (angle, side, angle).
4cm
4cm
30°
75°
75° 30°

14. Any one of the following four conditions is sufficient for two triangles to be congruent.
Condition 4(RHS):
‘Both triangles have a right angle, an equal hypotenuse and another equal side.’
This condition is known as RHS (right angle, hypotenuse, side).
4cm
9cm
4cm
9cm

15. Q2. Show that given triangles are congruent

16. Prove that triangles are congruent

19. Activity 1:
• Define congruency :
• Write all rules

20. Activity : 2 Shade congruent shapes with
same color

21. Once you have shown that triangle ABC is congruent to triangle PQR by
one of the above conditions, it means that:
A = P AB = PQ
B = Q BC = QR
C = R AC = PR
In other words, the points ABC correspond exactly to the points PQR in
that order. Triangle ABC is congruent to PQR can be written as ΔABC ≡
ΔPQR.
A
B
C
P
R
Q

22. ACTIVITY

23. ABCD is a kite. Prove that triangle ABC is congruent to triangle ADC.
Grade B Grade B
5cm
12cm 12cm
5cm
A
B
C
D
AB = AD
BC = CD
AC is common.
So: ΔABC = ΔADC (SSS)

24. Grade B
Grade B
The triangles in each pair are congruent. State the condition that shows that
the triangles are congruent.
5cm
3cm
75°
5cm
3cm
75°
5cm
7cm
4cm
5cm
7cm
4cm
7cm
5cm
7cm
5cm
8cm
35° 70°
8cm
35°
70°
a) b)
c) d)

25. Grade A
Grade A
Draw a rectangle EFGH. Draw in the
diagonal EG. Prove that triangle EFG
is congruent to triangle EHG.
Draw an isosceles triangle ABC
where AB = AC. Draw the line from
A to X, the midpoint of BC. Prove
that triangle ABX is congruent to
triangle ACX.
In the diagram
ABCD and DEFG
are squares. Use
congruent triangles
to prove that AE =
CG.
Jez says that these two triangles
are congruent because of ASA.
Explain why he is wrong.
3cm
42° 35°
3cm
42° 35°

26. Why did you draw that face?