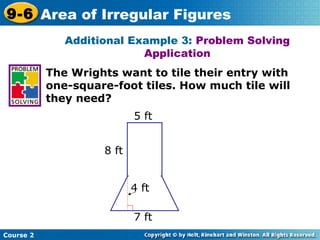
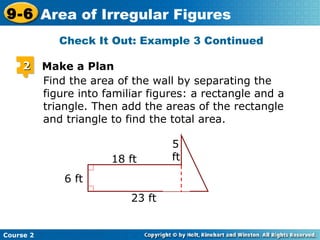
This document discusses finding the area of irregular figures by breaking them into familiar geometric shapes. It provides examples of estimating the area of irregular figures using graph paper, as well as calculating the exact area by decomposing figures into components like rectangles, triangles, parallelograms, and semicircles. Students are shown how to write out the steps to find each area component and then add them together to get the total area of the irregular figure. The final example problem asks students to determine how much tile or wallpaper is needed to cover irregularly shaped surfaces.

1. 9-6 Area of Irregular Figures
Course 2
Warm UpWarm Up
Lesson PresentationLesson Presentation
Problem of the DayProblem of the Day

2. Warm Up
Find the area of the following figures.
1. A triangle with a base of 12.4 m and a
height of 5 m
2. A parallelogram with a base of 36 in. and
a height of 15 in.
3. A square with side lengths of 2.05 yd
Course 2
9-6 Area of Irregular Figures

3. Problem of the Day
It takes a driver about second to begin
breaking after seeing something in the
road. How many feet does a car travel in
that time if it is going 10 mph? 20 mph?
30 mph?
11 ft; 22 ft; 33 ft
Course 2
9-6 Area of Irregular Figures
3
4

4. Learn to find the area of irregular figures.
Course 2
9-6 Area of Irregular Figures

5. You can find the area of an irregular
figure by separating it into non-
overlapping familiar figures. The sum of
the areas of these figures is the area of
the irregular figure. You can also
estimate the area of an irregular figure
by using graph paper.
Course 2
9-6 Area of Irregular Figures

6. Additional Example 1: Estimating the Area of an
Irregular Figure
Estimate the area of the figure. Each square
represents one square yard.
Count the number of filled or
almost-filled squares: 46 squares.
Count the number of squares that
are about half-full: 10 squares.
Add the number of filled squares plus
½ the number of half-filled
squares: 46 + ( • 10) = 48 + 5 =511
2
The area of the figure is about 51 yd2
.
Course 2
9-6 Area of Irregular Figures

7. Check It Out: Example 1
Estimate the area of the figure. Each square
represents one square yard.
Count the number of filled or
almost-filled squares: 11 red
squares.
Count the number of squares that
are about half-full: 8 green squares.
Add the number of filled squares plus
½ the number of half-filled
squares: 11 + ( • 8) = 11 + 4 =15.1
2
The area of the figure is about 15 yd .
2
Course 2
9-6 Area of Irregular Figures

8. Additional Example 2: Finding the Area of an
Irregular Figure
Find the area of the irregular figure. Use 3.14
for π.
Use the formula for the
area of a parallelogram.
Substitute 16 for b.
Substitute 9 for h.
A = bh
A = 16 • 9
A = 144
Step 1: Separate the figure into
smaller, familiar figures.16 m
Course 2
9-6 Area of Irregular Figures
9 m
16 m
Step 2: Find the area of each
smaller figure.
Area of the parallelogram:

9. Additional Example 2 Continued
Find the area of the irregular figure. Use 3.14
for π.
Substitute 3.14 for π
and 8 for r.
16 m
Course 2
9-6 Area of Irregular Figures
9 m
16 m
Area of the semicircle:
A = (πr)
1
2
__
The area of a semicircle
is the area of a circle.
1
2
A ≈ (3.14 • 82
)
1
2
__
A ≈ (200.96)
1
2
__
Multiply.A ≈ 100.48

10. Additional Example 2 Continued
Find the area of the irregular figure. Use 3.14
for π.
A ≈ 144 + 100.48 = 244.48
The area of the figure is about
244.48 m2
.
Step 3: Add the area to find the
total area.16 m
Course 2
9-6 Area of Irregular Figures
9 m
16 m

11. Check It Out: Example 2
Find the area of the irregular figure. Use 3.14
for π.
Use the formula for the
area of a rectangle.
Substitute 8 for l.
Substitute 9 for w.
A = lw
A = 8 • 9
A = 72
Step 1: Separate the figure into
smaller, familiar figures.
3 yd
Course 2
9-6 Area of Irregular Figures
9 yd Step 2: Find the area of each
smaller figure.
Area of the rectangle:
8 yd
9 yd

12. Check It Out: Example 2 Continued
Find the area of the irregular figure. Use 3.14
for π.
Substitute 2 for b and
9 for h.
Course 2
9-6 Area of Irregular Figures
Area of the triangle:
A = bh
1
2
__
The area of a triangle
is the b • h.
1
2
A = (2 • 9)
1
2
__
A = (18)
1
2
__
Multiply.A = 9
2 yd
9 yd
8 yd
9 yd

13. Check It Out: Example 2 Continued
Find the area of the irregular figure. Use 3.14
for π.
A = 72 + 9 = 81
The area of the figure is about 81 yd2
.
Step 3: Add the area to find the total area.
Course 2
9-6 Area of Irregular Figures

14. Additional Example 3: Problem Solving
Application
The Wrights want to tile their entry with
one-square-foot tiles. How much tile will
they need?
Course 2
9-6 Area of Irregular Figures
5 ft
8 ft
4 ft
7 ft
t

15. Additional Example 3 Continued
Course 2
9-6 Area of Irregular Figures
11 Understand the Problem
Rewrite the question as a statement.
• Find the amount of tile needed to cover the
entry floor.
List the important information:
• The floor of the entry is an irregular shape.
• The amount of tile needed is equal to the
area of the floor.

16. Additional Example 3 Continued
Course 2
9-6 Area of Irregular Figures
Find the area of the floor by separating the
figure into familiar figures: a rectangle and a
trapezoid. Then add the areas of the rectangle
and trapezoid to find the total area.
22 Make a Plan
5 ft
8 ft
4 ft
7 ft
t

17. Additional Example 3 Continued
Course 2
9-6 Area of Irregular Figures
Solve33
Find the area of each smaller figure.
A = lw
A = 8 • 5
A = 40
Area of the rectangle: Area of the trapezoid:
A = 24
A = h(b1 + b2)
1
2
__
A = • 4(5 + 7)
1
2
__
A = • 4 (12)
1
2
__
Add the areas to
find the total area.
A = 40 + 24 = 64
The Wrights’ need 64 ft2
of tile.

18. Additional Example 3 Continued
Course 2
9-6 Area of Irregular Figures
Look Back44
The area of the entry must be greater than
the area of the rectangle (40 ft2
), so the
answer is reasonable.

19. Check It Out: Example 3
The Franklins want to wallpaper the wall
of their daughters loft. How much
wallpaper will they need?
Course 2
9-6 Area of Irregular Figures
6 ft
23 ft
18 ft
5
ft

20. Check It Out: Example 3 Continued
Course 2
9-6 Area of Irregular Figures
11 Understand the Problem
Rewrite the question as a statement.
• Find the amount of wallpaper needed to
cover the loft wall.
List the important information:
• The wall of the loft is an irregular shape.
• The amount of wallpaper needed is equal to
the area of the wall.

21. Check It Out: Example 3 Continued
Course 2
9-6 Area of Irregular Figures
Find the area of the wall by separating the
figure into familiar figures: a rectangle and a
triangle. Then add the areas of the rectangle
and triangle to find the total area.
22 Make a Plan
6 ft
23 ft
18 ft
5
ft

22. Check It Out: Example 3 Continued
Course 2
9-6 Area of Irregular Figures
Solve33
Find the area of each smaller figure.
A = lw
A = 18 • 6
A = 108
Area of the rectangle: Area of the triangle:
Add the areas to
find the total area.
A = 108 + 27.5 = 135.5
The Franklin’s need 135.5 ft2
of wallpaper.
A = 27.5
A = bh
1
2
__
A = (5 • 11)
1
2
__
A = (55)
1
2
__

23. Check It Out: Example 3 Continued
Course 2
9-6 Area of Irregular Figures
Look Back44
The area of the wall must be greater than
the area of the rectangle (108 ft2
), so the
answer is reasonable.

24. Homework
Textbook PG 544-545 #'s
1-15
Due Thursday!!!!!
Insert Lesson Title Here
Course 2
9-6 Area of Irregular Figures