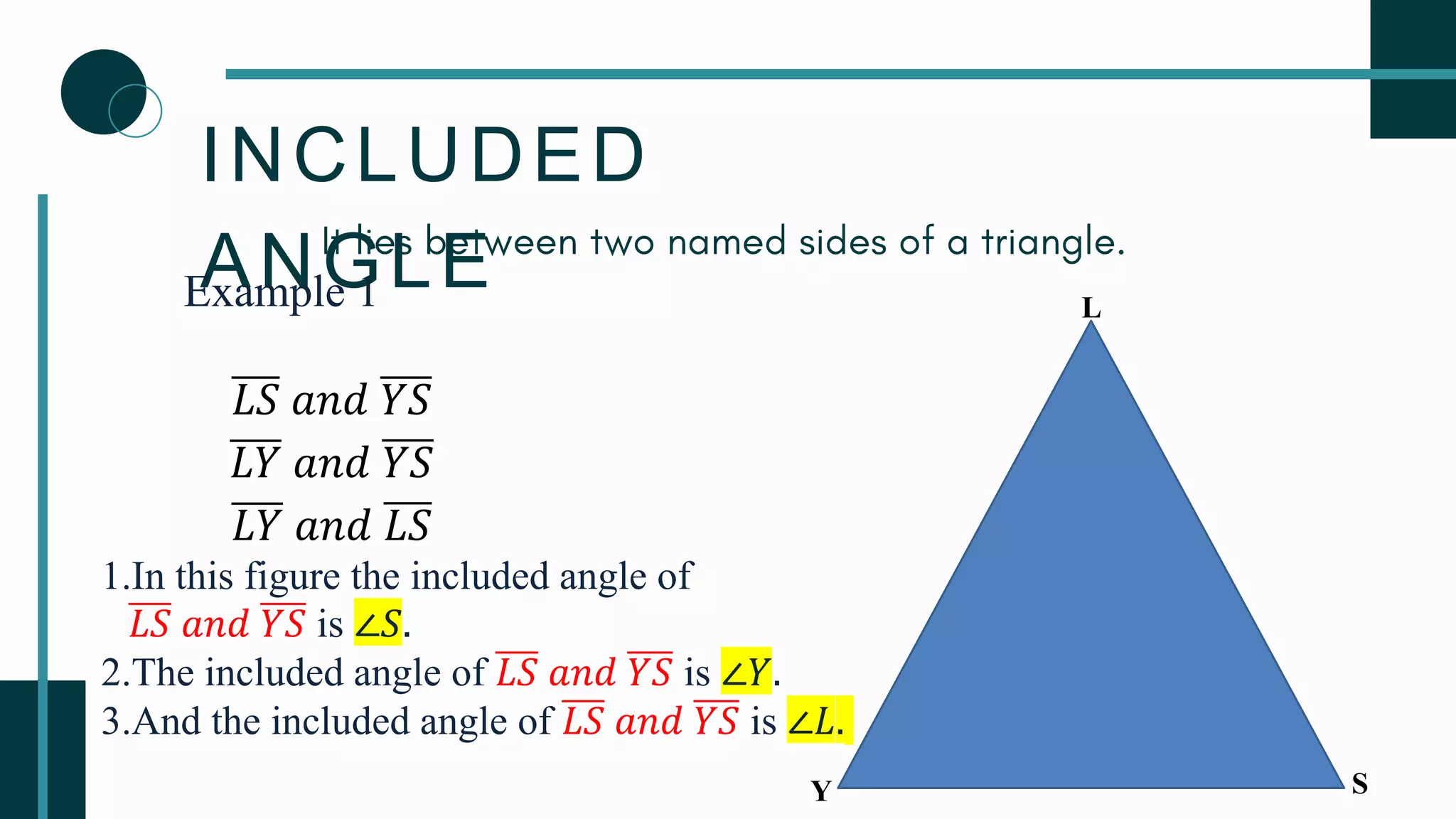
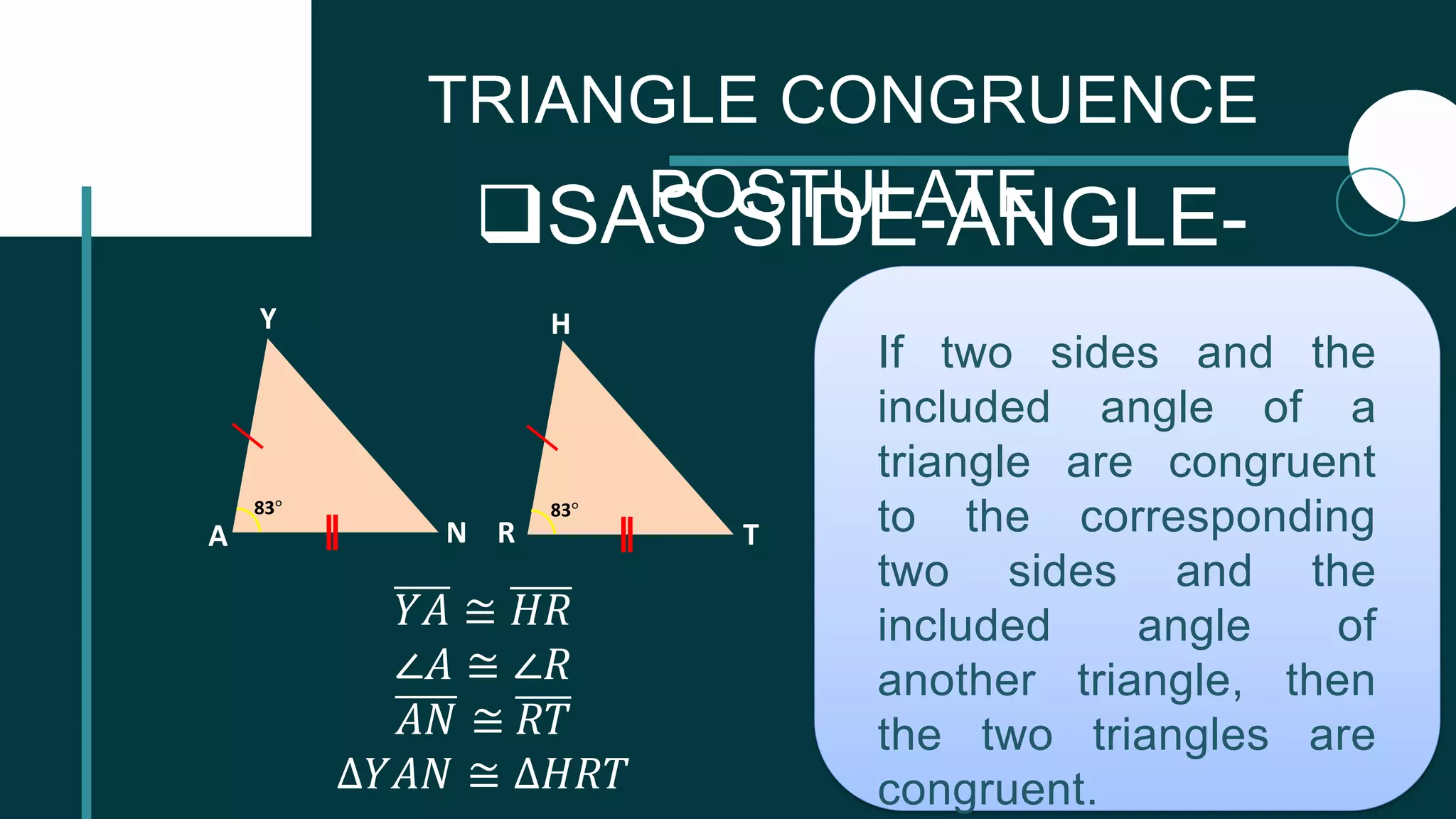
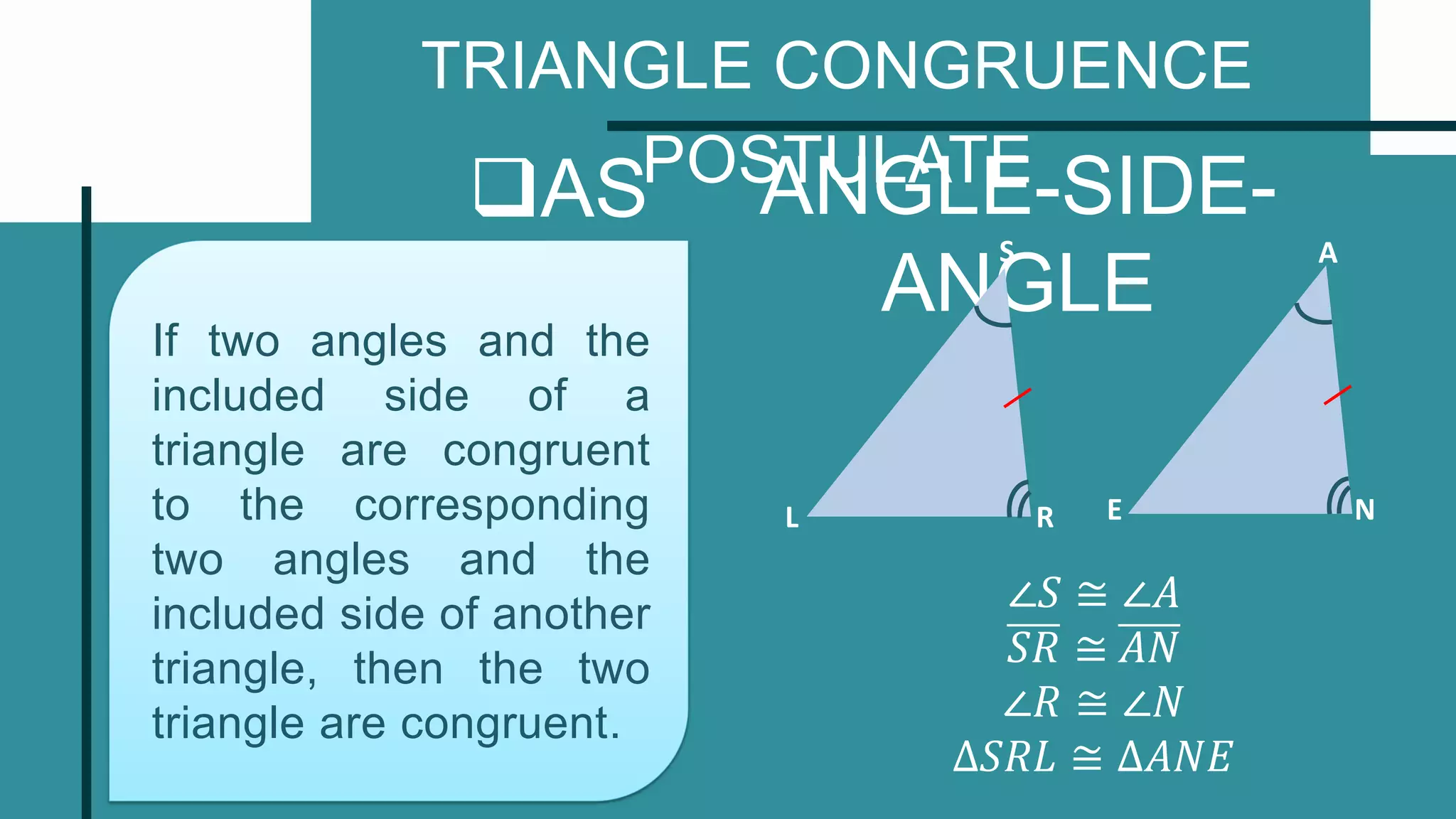
This document provides instruction on identifying included angles and sides of triangles and using the triangle congruence postulates SSS, SAS, and ASA. It contains examples of naming included angles when given two sides of a triangle and included sides when given two angles of a triangle. The three congruence postulates - side-side-side, side-angle-side, and angle-side-angle - are defined as well as examples of how to use each one to prove triangles are congruent. The document concludes with practice problems asking the reader to identify the missing part needed to prove triangles congruent using the postulates.

1. ILLUSTRATING THE
SAS, ASAAND SSS
CONGRUENCE
POSTULATE

2. At the end of the
lesson, you are
expected to:

3. Activity 1: Choose me correctly!
1. Write a congruence statement for the triangles.
A. ΔLMN  ΔRTS
B. ΔLMN  ΔSTR
C. ΔLMN  ΔRST
D. ΔLMN  ΔTRS

4. 2. Name the corresponding congruent angles for the
congruent triangles.
A. L  R, N  T, M  S
B. L  R, M  S, N  T
C. L  T, M  R, N  S
D. L  R, N  S, M  T

5. 3. Given ∆𝑅𝑂𝐹, what is the included angle between
𝑅𝑂 𝑎𝑛𝑑 𝑂𝐹?
A.∠𝐹
B.∠𝑂
C.∠𝑅
D.∠𝐹𝑅𝑂
4. In ∆𝑁𝐸𝑇, what side is included between ∠𝑁 and ∠𝑇?
A.𝑁𝑇
B.𝑁𝐸
C.𝐸𝑇
D.𝑇𝐸

6. 5. Given that ΔABC  ΔDEF, which
of the following statements is true?
A. A  E
B. C  D
C. AB  DE
D. BC  FD

7. INCLUDED AND
NON-INCLUDED
PARTS OF
TRIANGLE

8. INCLUDED
ANGLE L
S
Y
Example 1
𝐿𝑆 𝑎𝑛𝑑 𝑌𝑆
𝐿𝑌 𝑎𝑛𝑑 𝑌𝑆
𝐿𝑌 𝑎𝑛𝑑 𝐿𝑆
1.In this figure the included angle of
𝐿𝑆 𝑎𝑛𝑑 𝑌𝑆 is ∠𝑆.
2.The included angle of 𝐿𝑆 𝑎𝑛𝑑 𝑌𝑆 is ∠𝑌.
3.And the included angle of 𝐿𝑆 𝑎𝑛𝑑 𝑌𝑆 is ∠𝐿.

9. What is your observation to example number 1?
OBSERVATION:
The common vertex or common endpoint of the two named sides
is the included angle.
Example 2
𝐸𝐽 𝑎𝑛𝑑 𝐸𝑀
𝑀𝐽 𝑎𝑛𝑑 𝐸𝑀
𝐸𝐽 𝑎𝑛𝑑 𝐽𝑀
1.The common vertex of 𝐸𝐽 𝑎𝑛𝑑 𝐸𝑀
is ∠𝐸.
2.The common vertex of 𝑀𝐽 𝑎𝑛𝑑 𝐸𝑀
is ∠𝑀.
3.The common vertex of 𝐸𝐽 𝑎𝑛𝑑 𝐽𝑀 is
∠𝐽.

10. INCLUDED
SIDE
It is lies between two named angles of the triangle.
L
E
I
∠𝐸 𝑎𝑛𝑑 ∠𝐼
∠𝐿 𝑎𝑛𝑑 ∠𝐼
∠𝐸𝐿𝐼 𝑎𝑛𝑑 ∠𝐼𝐸𝐿
Example 1:
1. In this figure the included side of
∠𝐸 𝑎𝑛𝑑 ∠𝐼 is 𝐼𝐸
2. The included side of ∠𝐿 𝑎𝑛𝑑 ∠𝐼 is
𝐼𝐿
3. And the included side of
∠𝐸𝐿𝐼 𝑎𝑛𝑑 ∠𝐼𝐸𝐿 is 𝐸𝐿

11. What is your observation to example number 1?
OBSERVATION:
The VERTICES of the two named angles determine an included
side.
Example 2
∠𝑁 𝑎𝑛𝑑 ∠𝐴
∠𝑅 𝑎𝑛𝑑 ∠𝐴
∠𝑁 𝑎𝑛𝑑 ∠𝑅
1. The included side of ∠𝑁 𝑎𝑛𝑑 ∠𝐴 is 𝑁𝐴
2. The included side of ∠𝑅 𝑎𝑛𝑑 ∠𝐴 is 𝑅𝐴
3. And the included side of ∠𝑁 𝑎𝑛𝑑 ∠𝑅 is 𝑁𝑅

12. TRIANGLE CONGRUENCE
POSTULATE
SSS
SAS
ASA

13. TRIANGLE CONGRUENCE
POSTULATE
SSS
SIDE-SIDE-
SIDE
If three sides of one
triangle are congruent
to the three
corresponding sides of
another triangle, then
the two triangles are
congruent.

14. TRIANGLE CONGRUENCE
POSTULATE
SSSSIDE-SIDE-
SIDE If three sides of one
triangle are congruent
to the three
corresponding sides of
another triangle, then
the two triangles are
congruent.
𝑺𝑯 ≅ 𝑵𝑴
𝑯𝑨 ≅ 𝑴𝑰
𝑺𝑨 ≅ 𝑵𝑰
∆𝑺𝑯𝑨 ≅ ∆𝑵𝑴𝑰
S
H A N
M I

15. TRIANGLE CONGRUENCE
POSTULATE
SAS SIDE-ANGLE-
SIDE
If two sides and the
included angle of a
triangle are congruent
to the corresponding
two sides and the
included angle of
another triangle, then
the two triangles are
congruent.
A
Y
N R
H
T
83° 83°
𝑌𝐴 ≅ 𝐻𝑅
∠𝐴 ≅ ∠𝑅
𝐴𝑁 ≅ 𝑅𝑇
∆𝑌𝐴𝑁 ≅ ∆𝐻𝑅𝑇

16. TRIANGLE CONGRUENCE
POSTULATE
AS
A
ANGLE-SIDE-
ANGLE
If two angles and the
included side of a
triangle are congruent
to the corresponding
two angles and the
included side of another
triangle, then the two
triangle are congruent.
∠𝑆 ≅ ∠𝐴
𝑆𝑅 ≅ 𝐴𝑁
∠𝑅 ≅ ∠𝑁
∆𝑆𝑅𝐿 ≅ ∆𝐴𝑁𝐸
N
E
A
L R
S

17. D E T E R M I N E N E C E S S A R Y PA R T S T O
S H O W C O N G R U E N C E B E T W E E N
T R I A N G L E S
∆𝐿𝑌𝑆 ≅ ∆𝐿𝐼𝑆
∆𝐿𝑌𝑆 ≅ ∆𝐿𝐼𝑆
∠𝑌 ≅ ∠𝐼
∆𝐿𝑌𝑆 ≅ ∆𝐿𝐼𝑆
𝐿𝑌 ≅ 𝐿𝐼
S
I
L
Y

18. Assignment:
R
L
I
E
a. 𝑅𝐼 ≅ 𝑅𝐿
b. ∠𝐼 ≅ ∠𝐿
c. __________
∆𝑅𝐸𝐼 ≅ ∆𝑅𝐸𝐿 𝑏𝑦 𝑆𝐴𝑆

19. Assignment:
a. 𝐿𝐽 ≅ 𝐴𝑌
c. __________
∆𝐿𝐽𝑌 ≅ ∆𝐴𝑌𝐽 𝑏𝑦 𝑆𝑆𝑆
L
A
Y
J
b. 𝑌𝐽 ≅ 𝑌𝐽

20. THANK
YOU!