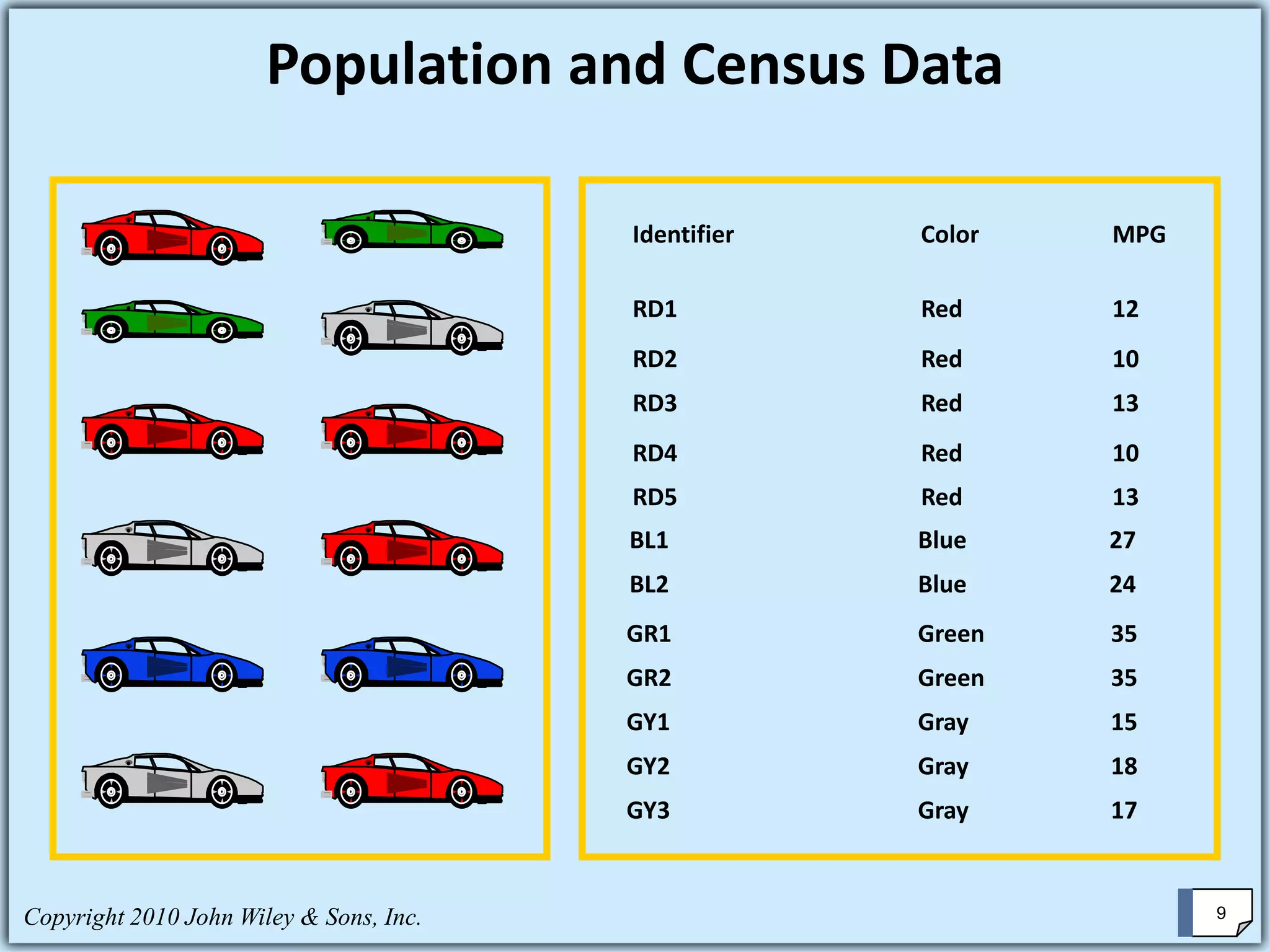
This document discusses key concepts in statistics. It defines statistics as the science of gathering, analyzing, interpreting, and presenting numerical data. There are two main types: descriptive statistics describe or reach conclusions about a group, while inferential statistics use sample data to reach conclusions about the larger population. The document outlines common applications of statistics in business and explains important statistical concepts like populations, samples, parameters, statistics, and different levels of data measurement.

1. Copyright 2010 John Wiley & Sons, Inc. 1
Copyright 2010 John Wiley & Sons, Inc.
Business Statistics, 6th ed.
by Ken Black
Chapter 1
What are
Statistics?

2. Copyright 2010 John Wiley & Sons, Inc. 2
Define statistics.
Become aware of a wide range of applications of
statistics in business.
Differentiate between descriptive and inferential
statistics.
Classify numbers by level of data and understand
why doing so is important.
Learning Objectives

3. Copyright 2010 John Wiley & Sons, Inc. 3
Statistics in Business
Accounting — auditing and cost estimation
Economics — regional, national, and international economic
performance
Finance — investments and portfolio management
Management — human resources, compensation, and quality
management
Management Information Systems — performance of systems
which gather, summarize, and disseminate information to
various managerial levels
Marketing — market analysis and consumer research
International Business — market and demographic analysis

4. Copyright 2010 John Wiley & Sons, Inc. 4
Science of gathering, analyzing, interpreting, and
presenting data on various topics
Branch of mathematics
Course of study
Facts and figures
Measurement taken on a sample
Type of distribution being used to analyze data
What is Statistics?

5. Copyright 2010 John Wiley & Sons, Inc. 5
Statistics – science dealing with the collection,
analysis, interpretation, and presentation of
numerical data
Statistics has two types
Descriptive measure – computed from a sample and
used to make a determination
Distribution - used in the analysis of the data
Statistics in Business

6. Copyright 2010 John Wiley & Sons, Inc. 6
Branches of statistics
Descriptive – using data gathered on a group to describe
or reach conclusions about the group
Inferential – data gathered from a sample and used to
reach conclusions about the population from which the
data was gathered
Used to draw conclusions about the group or similar groups
Statistics in Business

7. Copyright 2010 John Wiley & Sons, Inc. 7
Population — the whole
a collection of persons, objects, or items under study
Census — gathering data from the entire population
Sample — a portion of the whole/population
a subset of the population; must be large enough to
represent the whole
Population Versus Sample

8. Copyright 2010 John Wiley & Sons, Inc. 8
Population

9. Copyright 2010 John Wiley & Sons, Inc. 9
Identifier Color MPG
RD1 Red 12
RD2 Red 10
RD3 Red 13
RD4 Red 10
RD5 Red 13
BL1 Blue 27
BL2 Blue 24
GR1 Green 35
GR2 Green 35
GY1 Gray 15
GY2 Gray 18
GY3 Gray 17
Population and Census Data

10. Copyright 2010 John Wiley & Sons, Inc. 10
Sample and Sample Data
Identifier Color MPG
RD2 Red 10
RD5 Red 13
GR1 Green 35
GY2 Gray 18

11. Copyright 2010 John Wiley & Sons, Inc. 11Copyright 2010 John Wiley & Sons, Inc. 11
Parameter vs. Statistic
Parameter — descriptive measure of the population
Usually represented by Greek letters
Statistic — descriptive measure of a sample
Usually represented by Roman letters

12. Copyright 2010 John Wiley & Sons, Inc. 12Copyright 2010 John Wiley & Sons, Inc. 12
parameterpopulationdenotes
2
 denotes population variance
 denotes population standard deviation
Symbols for Population Parameters

13. Copyright 2010 John Wiley & Sons, Inc. 13Copyright 2010 John Wiley & Sons, Inc. 13
meansampledenotesx
2
S denotes sample variance
S denotes sample standard deviation
Symbols for Sample Statistics

14. Copyright 2010 John Wiley & Sons, Inc. 14Copyright 2010 John Wiley & Sons, Inc. 14
Process of Inferential Statistics
)(parameter
Population1.

)(statistic
x
Sample3.
estimateto
xCalculate4.
samplerandom
aSelect2.

15. Copyright 2010 John Wiley & Sons, Inc. 15Copyright 2010 John Wiley & Sons, Inc. 15
Statistics in Business
Difference between a parameter and statistic is only
important in the use of inferential statistics
Calculations of parameter can be cost prohibitive
When cost prohibitive, a sample calculates appropriate statistics.
Researchers use the calculation as an estimate of the parameter.

16. Copyright 2010 John Wiley & Sons, Inc. 16Copyright 2010 John Wiley & Sons, Inc. 16
Statistics in Business
Inferences about parameters made under conditions
of uncertainty
Uncertainty can be caused by
small sample
lack of knowledge about the source of the inferences
change in conditions not accounted for

17. Copyright 2010 John Wiley & Sons, Inc. 17Copyright 2010 John Wiley & Sons, Inc. 17
Statistics in Business
Probability statement – used to estimate the
level of confidence in the probability statement

18. Copyright 2010 John Wiley & Sons, Inc. 18
Nominal — In nominal measurement the numerical
values just "name" the attribute uniquely.
No ordering of the cases is implied. For example, jersey
numbers in basketball are measures at the nominal level.
A player with number 30 is not more of anything than a
player with number 15, and is certainly not twice
whatever number 15 is.
Levels of Data Measurement

19. Copyright 2010 John Wiley & Sons, Inc. 19
Ordinal - A variable is ordinal measurable if ranking is
possible for values of the variable.
For example, a gold medal reflects superior performance to
a silver or bronze medal in the Olympics, or you may prefer
French toast to waffles, and waffles to oat bran muffins.
“First,” “Second” are ordinal measurements.
Levels of Data Measurement

20. Copyright 2010 John Wiley & Sons, Inc. 20
Interval - In interval measurement the distance
between attributes does have meaning.
For example, when measuring temperature (in Fahrenheit),
the distance from 30-40 is same as the distance from 70-80.
The interval between values is interpretable.
Levels of Data Measurement

21. Copyright 2010 John Wiley & Sons, Inc. 21
Ratio — in ratio measurement there is always an
absolute zero that is meaningful.
This means that you can construct a meaningful fraction
(or ratio) with a ratio variable.
In applied social research most "count" variables are ratio,
for example, the number of clients in past six months.
Levels of Data Measurement

22. Copyright 2010 John Wiley & Sons, Inc. 22
Cardinal - A variable is cardinally measurable if a given
interval between measures has a consistent meaning,
i.e., if the measure corresponds to points along a
straight line.
For example, height, output, and income are cardinally
measurable
Levels of Data Measurement

23. Copyright 2010 John Wiley & Sons, Inc. 23
Nominal Level Data
Numbers are used to classify or categorize
Example: Employment Classification
1 for Educator
2 for Construction Worker
3 for Manufacturing Worker

24. Copyright 2010 John Wiley & Sons, Inc. 24
Ordinal Level Data
Numbers are used to indicate rank or order
Relative magnitude of numbers is meaningful
Differences between numbers are not comparable
Example: Ranking productivity of employees
Example: Position within an organization
1 for President
2 for Vice President
3 for Plant Manager
4 for Department Supervisor
5 for Employee

25. Copyright 2010 John Wiley & Sons, Inc. 25
Faculty and staff should receive preferential
treatment for parking space.
Ordinal Data
1 2 3 4 5
Strongly
Agree
Agree Strongly
Disagree
DisagreeNeutral

26. Copyright 2010 John Wiley & Sons, Inc. 26
Interval Level Data
Interval Level data - Distances between consecutive
integers are equal
Relative magnitude of numbers is meaningful
Differences between numbers are comparable
Location of origin, zero, is arbitrary
Vertical intercept of unit of measure transform function is
not zero
Example: Fahrenheit Temperature
Example: Monetary Utility

27. Copyright 2010 John Wiley & Sons, Inc. 27
Highest level of measurement
Relative magnitude of numbers is meaningful
Differences between numbers are comparable
Location of origin, zero, is absolute (natural)
Vertical intercept of unit of measure transform function
is zero
Examples: Height, Weight, and Volume
Example: Monetary Variables, such as Profit and Loss,
Revenues, Expenses, Financial ratios - such as P/E
Ratio, Inventory Turnover, and Quick Ratio.
Ratio Level Data

28. Copyright 2010 John Wiley & Sons, Inc. 28
Ratio Level Data
Parametric statistics – requires that the data be
interval or ration
Non Parametric – used if data are nominal or ordinal
Non parametric statistics can be used to analyze interval
or ratio data

29. Copyright 2010 John Wiley & Sons, Inc. 29Copyright 2010 John Wiley & Sons, Inc. 29
Data Level
Nominal
Ordinal
Interval
Ratio
Meaningful Operations
Classifying and Counting
All of the above plus Ranking
All of the above plus Addition,
Subtraction, Multiplication, and
Division
All of the above
Statistical
Methods
Nonparametric
Nonparametric
Parametric
Parametric
Data Level, Operations, and
Statistical Methods