The document discusses the optical properties of a dimer of plasmonic nanospheres using the multipole spectral expansion (MSE) method. MSE allows calculation of the potential at any point by separating geometric and dielectric properties, and can be extended to dimers and multimers. For a dimer, MSE derives matrix elements describing the interactions between the nanospheres. Translated eigenstates are used to describe the eigenstates of each individual nanosphere. Future work will apply this method to study field enhancement in nanosphere dimers.

1. by
SHIPRA CHOUDHARY
14/MAP/007
M.Sc. (Applied Physics)
Under the guidance of
Dr. Manmohan Singh Shishodia
Gautam Buddha University, Greater Noida
Otical propertIes of dimer of plasmonIc nanosphere

2.  Why Nanomaterials?
 Advantages of Dimer over Single Nanosphere
 Introduction
 Multipole Spectral Expansion method (MSE)
 MSE method for single nanoshere
 MSE method for dimer of nanaosphere
 Dimer Matrix Elements
 Translated Eigenstates
 Future plan
outlines

3. Why nanomaterials?
• Material that has unique or novel properties, due to the
nanoscale ( nano metre- scale) structuring.
• The properties of the nanomaterials can be different from
bulk material:
 Larger surface area
 Quantum effect begins to dominate
Solar cells
Nanoantenna’s
(Metal Nanoparticles)
Nanoantenna’s
(Silicon Nanoparticles)

4. Advantages of dimer over single nanoparticles
 Dimer provides a stronger electric field
in than gap region than a single metallic
nanoparticle does in its proximity.
 Dimer plays the role of a nanolens to focus
the incident wave into a small hotspot re-
gion around the gap.
 Dimer plays the role of an antenna.
 Lesser the gap, greater is the electric field enhancement factor.
dm m
b
LR RR
**[ref: Jiunn-Woei Liaw, Jeng-Hong chen, chi-San, and Mao-Kuen kuo, Opt.Express 16,
13532-13540 (2009).]
3.0 3.2 3.4 3.6 3.8 4.0 4.2 4.4
0
1000
2000
3000
4000
5000
6000
7000
Fieldenhancement()
Frequency (eV)
a/r = 0.6
a/r = 0.7
a/r = 0.8
a/r = 0.9
a/r = 1.0

5.  Introduced by Fuchs and further developed by Bergman,
Milton and stockman.
 Analytical approach for calculating potential at any point.
 Separates the geometrical and dielectric properties and can
be extended to arbitrary combination of nanoparticles.
 Extendible to dimers and multimers.
 Dimer nanostructures may induce a relatively intense local
EMF within the dimer gap region and in the proximity of MNS.
**[ref: D. J. Bergman, Phys. Rep. 43, 377 (1978).]
MULTIPOLE SPECTRAL EXPANSION METHOD

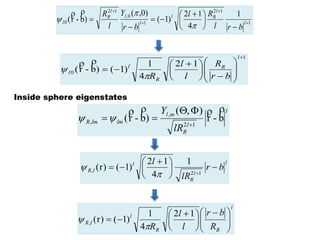
6. The overall potential expression in this approach
External potential
MSE METHOD FOR Single nanosphere
**[fig ref:Manmohan S. Shihodia, Boris D. Fainberg, and Abraham Nitzen, “Theory of energy
transfer interactions near sphere and nanoshell based plasmonic nanostructures”, SPIE 0277-
786X (2011).]
)()(φ|)()(
s)(s
s
)(φ)φ( extext rrrrrr mlml
ml l
l




 
surface)on theR(rθcosREθcosrEΦ 00ext 
R
P
zO
r
E0 zˆ
ε(ω)
hε
θ

7. 








 h
h
ε2ε(ω)
εε(ω)
s)(ωs
s
The dielectric part
The total potential outside the sphere
  )1for(3/112s  lll
 hεε(ω)1
1
)(ωs


,
  1
12
(1/2)12
m,
m,
r
R
R
φ),(θY
)r(ψ 


 l
l
l
l
l
l
θcos
r
R
π
3
2
1
)r(ψ 2
2/3
,01 

The potential eigenfunctions
The induced potential
Using Green’s first identity in the overlap integral
3/2RE
3
4π
I 0m, l
θcos
r
R
E
ε2ε(ω)
εε(ω)
)r(Φ 2
3
0
h
h
induced










θcos
r
R
E
ε2ε(ω)
εε(ω)
cosθrE)r(Φ 2
3
0
h
h
0out 










8. Nanosphere dimer
)r(ψ|ψ))((
)(
)r()r( '0'
,
,
,
',
'
b,la,lablal
RLa
la
RLb
lb
bl
ext BB
ss
s



 

 


   

The potential for two sphere geometry
Eigenvalue equation
)(ψ)(ψs rr  
Eigenvalues and eigenvectors of gamma









'',,,,,'',,,,,
'',,,,,'',,,,,
mlRightmlRightmlLeftmlRight
mlRightmlLeftmlLeftmlLeft
 
m d
'rr
LR
LO
RR
RO
b
L R
P
Z
zE ˆ0

9.  )b-r(ψψrθd
1'2
'
m'l',L
3
'',;,



 
*
l,m
V
mlml
l
l
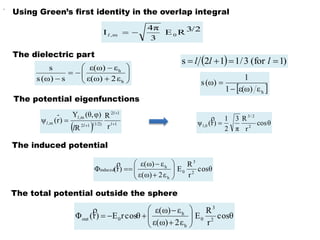
Using Green’s identity
dimer matrix elementS
)(
)(
12
''
L
''
,
*
,
Rr
2
'
'
,,,
br
r
r
dR
l
l
ml
ml
Lmlml







 


)]()([
)(
)()]([d
V
*
,
2
,
3
*
,
,
Rr
2
,
*
,
V
3
''''
L
'' rbrrd
r
r
brdRbrr mlmlL
ml
mlLmlmlL


 







),(
1
)( ,12,  ml
l
l
L
ml Yr
lR
r



),(
1
)( *
,12
*
,  ml
l
l
L
ml Yr
lR
r



),(
1)( *
,
1
12
*
,


ml
l
l
L
ml
Yr
lRr
r 





Eigenstates of left sphere

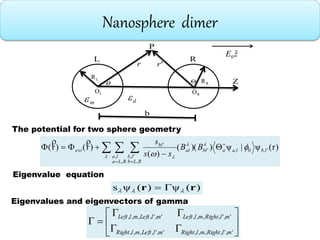
10. dimer matrix elementS
Eigenstates of right sphere
)(
1
)( '''
'
''
,1'
12
, brmll
l
R
ml
Y
brl
R
br 



 


),(),(
!)!12(!)!12(
!]!1)(2[
000
)12](1)(2)[12(4)1()(
1
),,1'
'
''
''''
''
,)1(
'''
''
''' bbmll
lm
brmll
YY
b
r
l
l
mm
llll
llY
br





 




















 



),(),(
!)!12(!)!12(
!]!1)(2[
000
)12](1)(2)[12(4)1()( '''
''
'
'
,,1'
'
''
''''
''
'
12
, bbmll
lm
l
R
ml
YY
b
r
l
l
mm
llll
ll
l
R
br 




 




















 
 

),(),(
!)!12(!)!12(
!]!1)(2[
000
)12](1)(2)[12(4)1(),(
12
'''
''
'
''
,,1'
'
''
''''
''
'
12
*
,
1
12
2
'
'
,,, bbmll
lm
l
R
Rr
ml
l
l
L
Lmlml
YY
b
r
l
l
mm
llll
ll
l
R
Yr
lR
l
dR
l
l
L





 







 














 


 
),(
!)!12(!)!12(
!]!1)(2[
000
)12](1)(2)[12(4
12
)1( ''
'
''
''
,'
'
''
''''
''
)2/1()2/1(
'
'
,,, bbmmll
l
R
l
Llm
mlml
Y
l
l
mmmm
llllllll
ll
b
R
b
R
l
ll



 

















 















11. dimer matrix elementS
!!
)!(
]!1)(2[
)!2()!2(
)1(
000
'
'
'
'''
'
ll
ll
ll
llllll ll 






  
)!()!()!()!(]!1)(2[
)!()!()!2()!2(
)1(
)(
''''
'''''
''
''
''
mlmlmlmlll
mmllmmllll
mmmm
llll mmll









 
bmmimm
llbbmmll
eP
mmll
mmllll 


 )(
''
'''
,
''
''' )(cos
)!(
)!(
4
]1)(2[
),(Y 




Using properties of Wigner 3j symbols
Relation b/w Spherical harmonics & Legendre functions
bmmimm
ll
l
R
l
Llm
mlml
eP
ll
ll
l
l
l
l
ll
ll
mlmlmlml
mmll
b
R
b
R
ll
l
llll
)(
'
'
'
'
'
'
''''
'')2/1()2/1(
'
'
''
,,,
''
'
'
'
''
!!
)(
!)!12(
)!2(
!)!12(
)!2(
]!1)(2[
!]!1)(2[
)!()!()!()!(
)!(
)12)(12(
12
]1)(2[
)1(


























bmmimm
ll
l
R
l
Llm
mlml
eP
mlmlmlml
mmll
ll
ll
b
R
b
R )'('
'''''
''
'
')2/1(')2/1(
)!()!()!()!(
)!(
)12)(12(
)1(
'
''





















12. TRANSLATED EIGENStates
Outside sphere eigenstates
1
,
12
b-r
),(
)b-r( 


 l
ml
l
R
lm
Y
l
R



1
,
12
),(
)b-r( 


 l
ml
l
R
lm
R
Y
l
R













b,renwh1
b,rwhen1
cos
br
br









b,rnwhe0
b,rwhen
 
m d
'rr
LR
LO
RR
RO
b
L R
P
Z
zE ˆ0

13. 1
0
12
4
1
)1()b-r(















 

l
R
R
l
l
br
R
l
l
R


1
12
1
0,
12
0
1
4
12
)1(
)0,(
)b-r( 









 


 l
l
Rl
l
l
l
R
l
brl
Rl
br
Y
l
R




Inside sphere eigenstates
l
l
R
ml
lmlmR
lR
Y
b-r
),(
)b-r(
12
,
,




l
l
R
l
lR br
lR
l





 

12,
1
4
12
)1()r(


l
RR
l
lR
R
br
l
l
R 




 





 

12
4
1
)1()r(,



14. Future plan
 To Calculate the external potential and overlap integral for a pair
of metallic nanoparticles (dimer) to obtain the overall potential in
the gap region.
 To study the effect of Electric Field Enhancement, polarizability
and plexcitonic interactions in the vicinity and the gap region of a
pair of metallic nanoparticles (dimer).
 To explore different plasmonic materials other than metals(Au or
Ag).
 To extend Multipole Spectral Expansion Method to treat
Nanoshells.

15. references
 Manmohan S. Shishodia, Boris D. Fainberg, and Abraham Nitzen, “Theory of energy
transfer interactions near sphere and nanoshell based plasmonic nanostructures”,
SPIE 0277-786X (2011).
 J.D. Jackson, “Classical Electrodynamics”, John Wiley & Sons, (1998).
 D.J. Bergman, “Dielectric constant of a two-component granular composite: A
practical scheme for calculating the pole spectrum”, phys. Rev. B, 19, 2359 (1979).
 M. Danos, and L.C. Maximon, “Multipole matrix elements of the translation
operator”, J. Mathematical Phys. 6, pp. 766-778 (1965).
 http://functions.wolfram.com/Polynomials/SphericalHarmonicY/20/01/02
 http://mathworld.wolfram.com/Polynomials/Wigner3j-Symbol.html
 Jiunn-Woei Liaw, Jeng-Hong chen, chi-San, and Mao-Kuen kuo, “Purecell effect of
nanoshell dimer on single molecule’s fluoresecnce”, Opt.Express 16, 13532-13540
(2009).

16. THANKYOU