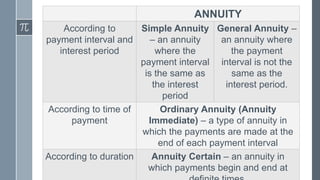
This document defines and provides examples of different types of annuities. It discusses simple and general annuities, ordinary and annuity certain annuities, and defines key terms like term, periodic payment, future value, and present value. Examples are provided to demonstrate calculating the future and present value of annuities given periodic payments, interest rates, and time periods.

1. Annuity

2. Annuity
An ANNUITY is a sequence of
equal payments (or deposits) made
at a regular interval of time.

3. ANNUITY
According to
payment interval and
interest period
Simple Annuity
– an annuity
where the
payment interval
is the same as
the interest
period
General Annuity –
an annuity where
the payment
interval is not the
same as the
interest period.
According to time of
payment
Ordinary Annuity (Annuity
Immediate) – a type of annuity in
which the payments are made at the
end of each payment interval
According to duration Annuity Certain – an annuity in
which payments begin and end at

4. DEFINITION OF TERMS
Term of an Annuity (t)
The time between the first payment
interval and the last payment interval.
Regular or Periodic
Payment (R)
The amount of each payment.
Amount (Future
Value) of an annuity
(F)
The sum of future value of all the
payments to be made during the entire
term of the annuity.
Present Value of an
annuity (P)
The sum of present value of all the
payments to be made during the entire
term of the annuity.

5. Example
Suppose Mrs. Manda would like to deposit P3,000
every month in a fund that gives 9%, compounded
monthly. How much is the amount of future value of
her savings after 6 months?
Given: Periodic payment (R) = P3,000
Term (t) = 6 months
Interest rate per annum (annually) (i) = 0.09/9%
Number of conversion per year (m) = 12
Interest rate per period 𝑗 =
݅
݉
=
𝟎.𝟎𝟗
𝟏𝟐
0.0075

7. (2) Add all the future values obtained from the
cash flow.
3,000 = 3,000.00
3,000 (1 + 0.0075) = 3,022.50
3,000 (1 + 0.0075) 2 = 3,045.17
3,000 (1 + 0.0075) 3 = 3,068.01
3,000 (1 + 0.0075) 4 = 3,091.02
3,000 (1 + 0.0075) 5 = 3,114.20
Php18,340.89
Thus, the amount of this annuity is P18,340.89

8. FUTURE VALUE

9. FUTURE VALUE
The future value of an ordinary annuity with regular
payments R at a nominal interest rate I compounded
m times a year after t years is
Note: j =
݅
݉
n = mt

10. Example 2
To start a business, Jake wants to save a
certain amount of money at the end of every
month to put in an account providing 2%
interest compounded monthly. His estimated
start-up capital is P150,000. If he wants to
start a business in 1.5 years, how much
monthly deposit must he put into the
account?

11. PRESENT VALUE

12. Julia borrowed an amount of money from
Marleah. She agrees to pay the principal plus
interest of 8% compounded quarterly by
paying Php 38 973. 76 each year for 3 years.
Determine the money barrowed by Julia (or the
present value of the annuity).
Example 3

13. PRESENT VALUE
The present value P of an ordinary annuity with
regular payments R at a nominal interest rate I
compounded m times a year after t years is
Note: j =
݅
݉
n = mt

14. Marco borrowed an amount of money from
Mike. He agrees to pay the principal plus
interest of 8% compounded quarterly by
paying Php 38 973. 76 each year for 3 years.
Determine the money barrowed by Marco (or
the present value of the annuity).
Example 3

15. Tin works very hard because she wants to
have enough money in her retirement account
when she reaches the age 60. She wants to
withdraw Php 30 000.00 every 3 months for 20
years starting 3 months after she retires. How
much must Tin deposit at retirement at 12%
per year compounded quarterly for the
annuity?
Example 4

16. The cash value or cash price of a
purchase is equal to the down payment
(if there is any) plus the present value
of the installment payment.

17. Mr. Lanchita paid Php 300,000 as a down
payment for a car. The remaining amount is to
be settled by paying Php 20,000 at the end of
each month for 5 years. If interest is 12%
compounded monthly, what is the cash price of
his car?
Example 5

18. ADD A SLIDE
TITLE - 4

19. ADD A SLIDE
TITLE - 5