Master Thesis

1
Bauhaus Universität-Weimar
Institute of Structural Mechanics
A Posteriori Error Estimation for Extended Finite Element Method
Presented by
Amir Rahimi
Supervisor
Prof. Dr.-Ing. Timon Rabczuk
Co-Supervisor
Ph.D Cosmin Anitescu
Summer 2012

2
Contents
Abstract . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
1. Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
1.1. Element and Approximation Technology . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
1.2. Computational Fracture Mechanics . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
1.3. A Posteriori Error Estimation in Finite Element Analysis . . . . . . . . . . . . . . . . . . . 10
1.4. Outline . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
2. One-Dimensional Problem . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
2.1. Model Problem . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
2.1.1. Strong Form . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
2.1.2. Weak Form and Discrete System . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
2.2. Finite Element Solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
2.3. Error Estimator. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
2.4. Implementation and Results-1D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
3. Two-Dimensional Problem . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43
3.1. Model Problem . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43
3.2. Overview of MXFEM . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45
3.2.1. Crack Enrichment Function . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50
3.2.2. Inclusion Enrichment Function . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54
3.2.3. Void Enrichment Function . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55
3.2.4. Element Integration with Discontinuity . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 56
3.3. Error Estimation in Bilinear Finite Element Approximation . . . . . . . . . . . . . . . . . 58
3.4. Implementation and Results-2D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 63

3
List of Figures
Figure 1-The one-dimensional model problem . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
Figure 2-A typical one-dimensional mesh of 4 elements. A linear shape function in
corresponding to node 3 with support of shape function . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
Figure 3-Interpolation between local and global coordinate system . . . . . . . . . . . . . . . . . . . . 17
Figure 4-Construction of recovery operator 𝑮 𝒉 from piecewise linear approximation in one
dimension . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
Figure 5-Error graphs for shifted Sukumar enrichment function, 10 nodes . . . . . . . . . . . . . . . 29
Figure 9-Error graphs for Unshifted Sukumar enrichment function, 10 nodes . . . . . . . . . . . . 30
Figure 10-Error graphs for Unshifted Sukumar enrichment function, 20 nodes . . . . . . . . . . . 31
Figure 13-Error graphs for Moes enrichment function, 10 nodes . . . . . . . . . . . . . . . . . . . . . . . 35
Figure 17-Error graphs for Unshifted Fries enrichment function, 10 nodes . . . . . . . . . . . . . . . 38
Figure 21-Error graphs for shifted Fries enrichment function, 10 nodes . . . . . . . . . . . . . . . . . 41

4
Figure 25-TWO-Dimensional Model Problem . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43
Figure 26-Example of a signed distance function for a closed domain . . . . . . . . . . . . . . . . . . 46
Figure 27-Example of a signed distance function for an open section . . . . . . . . . . . . . . . . . . . 47
Figure 28-Physical and parent 4-node elements . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 49
Figure 29-Selection of enriched nodes for 2D crack problem. Circled nodes are enriched by the
step function whereas the squared nodes are enriched by the crack tip functions. (a) on a
structured mesh; (b) on an unstructured mesh . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52
Figure 30-Coordinate configuration for crack tip enrichment function . . . . . . . . . . . . . . . . . . 53
Figure 31-Sub-triangulation of finite elements . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57
Figure 32-Construction of recovered gradient at vertex of element K. The value at • is a linear
combination of the values at o using the weights indicated . . . . . . . . . . . . . . . . . . . . . . . . . . . 59
Figure 33-The comparison of the exact and approximated solution for the zero body force . 65
Figure 34-Stress y-y distribution for the zero body force . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 65
Figure 35 - The comparison of the exact and approximated solution for the constant body
force . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67
Figure 36-the stress y-y distribution for the constant body force . . . . . . . . . . . . . . . . . . . . . . . 67
Figure 37-The comparison of the exact and approximated solution for the linear body force 69
Figure 38-The stress y-y distribution for the linear body force . . . . . . . . . . . . . . . . . . . . . . . . . 69

5
List of Tables
Table 1-Shifted Sukumar Enrichment Shape Function . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
Table 2-Unshifted Sukumar Enrichment Shape Function . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
Table 3-Moes Enrichment Shape Function . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34
Table 4-Unshifted Fries Enrichment Shape Function . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37
Table 5-Shifted Fries enrichment shape function . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
Table 6-Effectivity indices for zero body force . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 64
Table 7-Effectivity indices for constant body force . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 66
Table 8-Effectivity indices for linear body force . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68

6
Abstract
The eXtended Finite Element Method (XFEM) is implemented for modeling arbitrary
discontinuities in one- and two-dimensions domains. Due to the fact that the modeling of a
discontinuous field with standard finite element approximation presents unique challenges, the
extended finite element method is used to remove these difficulties by modeling strong as well
as weak discontinuities in the approximation space. In XFEM the standard finite element space
is enriched with special functions to help capture the challenging features of problem.
Enrichment functions may be discontinuous, their derivatives can be discontinuous or they can
be chosen to incorporate a known characteristic of the solution and all is done using the notion
of partition of unity.
The approximation outcome of XFEM analysis always contains the intrinsic error. In the
engineering problems, mostly the main concern of interest is the gradient of the finite element
approximations that their accuracy gets more deteriorated in the fact that these values are
discontinuous at border of elements. Therefore, some post processing approaches provide
more smoothed gradient that is superior to the approximation obtained by the untreated
gradient of the original finite element approximation. One approach that is opted to be
implemented in this thesis is a posteriori error estimation which is based on measuring the
difference between the direct and post-processed approximations to the gradient. The
technique that is here applied for a posteriori error estimation is based recovery method. In this
method by the definition of bench mark point, the approximation at each node is constructed
by averaging contribution from each of the elements surrounding the node. These values are
managed to produce the continuous approximation over the whole domain.

7
1. Introduction
This chapter provides an introduction to discontinuous enrichment in the finite element
framework, and a solution to measure the accuracy of this tool for approximated solution in
comparison to the exact solution without enhancing the exact equation. The introduction
consists of four sections. Section 1.1 reviews some advancements made in element and
approximation technology in the recent progress of finite element method (FEM). The method
developed in the field of fracture mechanics, and pertinent issues are reviewed in section 1.2.
The following section discusses a posteriori error estimation principles, and suggests its
advantages over the adaptivity and discontinuous enrichment methods. Finally, section 1.4
provides an outline of the remainder of the work.
1.1. Element and Approximation Technology
Finite element methods (FEM) have been widely used since their appearance six decades ago.
This popularity is due to their flexibility to deal with numerous problems and due to their
robustness. The FEM is used by scientists and engineers to investigate the dynamic failure of
structures, turbulent flow around an airfoil, heat transfer, and electromagnetism just to name a
few applications. While the finite element method is robust, it is not particularly well suited to
models involving discontinuities or singularities.
Due to the fact that standard finite element methods are based on piecewise differentiable
polynomial approximation (Galerkin method), they rely on an element topology for
construction of an approximating space. The construction of a discontinuous space with finite
elements necessitates the alignment of the element boundary with the geometry of the
discontinuity. Typically, finite element methods require significant mesh refinement or meshes
which conform with these features to get accurate results. This is not only computationally
costly and cumbersome but also results in loss of accuracy as the data is mapped from old mesh
to the new mesh. To compensate this deficiency of standard finite element methods, extended
finite elements have been developed.
The partition of unity approach (Melenk and Babuska 1996 [17]) offered a systematic
methodology to incorporate arbitrary functions into the finite element approximation space.
Due to this it is then possible to incorporate any kind of function to locally approximate the
field. These functions may include any analytical solution of the problem or any a priori
knowledge of the solution from the experimental test. From there, X-FEM is able to reproduce
the problematic features, i.e., discontinuities and the singularities, without changing mesh sizes
and dramatically improved results are obtained. Since the introduction of extended finite
element method by (Moes, Dolbow, and Belytschko 1999 [8]) it has been widely applied to
numerous solid mechanics problem such as 2-, and 3-dimensional crack growth problems

8
presented by Sukumar (2003) [23]. The XFEM also attains great simplicity of simulation for
interface problems like fluid-solid interaction to prevent computations that were formerly
tedious.
The enriched basis is formed by the combination of the nodal shape functions associated with
the mesh and the product of nodal shape functions with discontinuous functions. This
construction allows modeling of geometries that are independent of the mesh. Additionally, the
enrichment is added only locally i.e. where the domain needs to be enriched. The resulting
algebraic system of equations consists of two types of unknowns, i.e. standard degrees of
freedom and enriched degrees of freedom. Furthermore, the incorporation of enrichment
functions using the notion of partition of unity ensures the consistency of the solution. All the
above features provide the method with distinct advantages over standard finite element for
modeling arbitrary discontinuities.
1.2. Computational Fracture Mechanics
Of critical importance in computational fracture mechanics is the determination of the
parameters which characterize the stress and displacement field in the vicinity of the crack tip
or of the interface zone. For strong discontinuities, if the stress intensity factors exceed the
critical value of the material, crack growth and ultimately structural failure are possible. Several
strategies have been developed to extract mixed-mode intensity factors using contour integrals
derived from conservation laws. Moran (1987) [17] casts the essential issues in the general
framework of deriving domain integrals from momentum and energy-balance. The equivalent
domain integrals are viewed to be better suited for finite element calculations, as the same
Gauss quadrature points used for the construction of the bilinear form can be used to evaluate
the domain integrals.
A re-meshing technique is traditionally used for modeling discontinuities within the frame-work
of the finite element method. This is done near the discontinuity to align the element edges
with the boundary of discontinuity. This turns to be very expensive in computation only if the
discontinuity evolves in time, which would require generating a new mesh for each time
refinement. This leads to the construction of new shape functions and all the calculations have
to be repeated. Furthermore, the approximation solution is built on a history of previous states,
and whenever the mesh is changed, this history must be preserved. This is accomplished by
interpolation of data from old mesh to new mesh. The process of mapping variables from old
mesh to the new mesh comes with a loss of accuracy.
The idea of enriching the field with an analytical solution in the context of evolving
discontinuities was utilized by Gifford and Hilton (1978) [21], the displacement approximation
for an element was considered to be combination of the usual FEM shape function

9
displacement and the enriched displacement i.e. 𝑢 = 𝑢 𝑠𝑡𝑑 + 𝑢 𝑒𝑛𝑟 . The enriched part comes
from the displacement in the vicinity of discontinuity. The general idea of enriching the
approximation field was presented in Global-Local methodologies. The basic idea is aimed
towards reaching a global solution using a coarse grid of finite elements and then detailed
results are obtained by zooming to an area of interest (localization zones etc), refining the mesh
in the interest region and using the displacements from the global analysis as an input for the
refined mesh.
The work of Belytschko et al. (1998) [12] is one of the pioneering works toward the local
enrichment of the approximation field at an element level for the localization problems. His
work modified the strain field to get the required jumps in the strain field within the frame-
work of three-field variational principle. The three fields are the displacement 𝒖, strain 𝜖 and
the stress 𝜎. Embedded finite element method (EFEM) uses an element enrichment scheme,
where the field is modified or enriched within the framework of the three-field variational
principle. The enriched approximation to the field in generic from can be expressed as
𝒖 ≈ 𝑵 𝑠𝑡𝑑 𝒅 + 𝑵 𝑒𝑛𝑟 𝒅 𝑒 and 𝜖 ≈ 𝑩 𝑠𝑡𝑑 𝒅 + 𝑩 𝑒𝑛𝑟 𝒅 𝑒, where 𝑵 𝑠𝑡𝑑 and 𝑩 𝑠𝑡𝑑 are the standard FEM
displacement interpolation and strain-displacement interpolation matrices and 𝒅 are the FEM
standard degrees of freedom. 𝑵 𝑒𝑛𝑟 and 𝑩 𝑒𝑛𝑟 are the matrices containing enrichment terms for
the displacement and strain fields. 𝒅 𝑒 is the enriched degree of freedoms and are unknown.
These unknowns are found by imposing Drichlet and Neuwman boundary condition within the
element. The prominent feature in this method is that the enrichment is localized to an
element level. However, this method has a drawback the requirement of continuity along the
path of the crack. Extended finite element method (XFEM) on the contrary is also a local
enrichment scheme but uses the notion of partition of unity to incorporate an enrichment into
the approximating field. In XFEM, instead of an element enrichment scheme, a nodal
enrichment scheme is developed. A prominent feature of the partition of unity in XFEM or in
any partition of unity method is that it automatically enforces the conformity of the global
approximation space.
Extended finite element method (XFEM) introduced by Belytschko and Black (1999) [12] is able
to incorporate the local enrichment into the approximation space within the framework of
finite elements. The resulting enriched space is then capable of capturing the non-smooth
solutions with optimal convergence rate. The main scope of this thesis is to confirm the
convergence rate ratio obtained with XFEM in the case of the unavailability of the analytical
exact solution this is known as a posteriori error estimation.
The partition of unity finite element method (PUFEM) [14] defines set of functions over certain
domain 𝛺 𝑃𝑈𝐹𝐸𝑀
, such that they form a partition of unity, or in other words they sum up to 1.
This property lays on the basic rules of proposition for XFEM, and it corresponds to the ability of

10
the partition of unity shape functions to reproduce a constant, and this is essential for
convergence. The main idea of XFEM (or any partition of unity based method) lies in applying
the appropriate enrichment functions locally in the domain of interest using the partition of
unity. The XFEM brings the capability of tracking the discontinuity with coupling to level set
method. Level set method is a numerical technique to track the discontinuities. It is based on
the idea of defining a function such that the discontinuity is represented as the contour of the
zero level set function. Level set function not only helps in tracking arbitrarily aligned finite
element meshes but also helps in defining the enrichment function.
1.3. A Posteriori Error Estimation in Finite Element Analysis
After the advent of finite element method in the era of numerical simulation and mechanics, it
always brings the concern of error in calculations. Basically, there are two types of error
estimation procedures available. So called a priori error estimators provide information on the
asymptotic behavior of the discretization errors but are not designed to give an actual error
estimate for a given mesh. In contrast, a posteriori error estimators employ the finite element
solution itself to derive estimates of the actual solution errors. Numerical error is intrinsic in
mathematical simulation. No matter how sophisticated the mathematical model of an event is,
it is always subject to error. Discretization error can be large, pervasive, unpredictable by
classical heuristic means, and can invalidate numerical prediction. For these reasons, a
mathematical theory for estimating and quantifying discretization error is of paramount
importance to the computational solution. More importantly, knowledge of approximation
errors in simulation, as well as their distribution and magnitude provides the basis for adaptive
control of the numerical process, the meshing. This includes the choice of algorithms, and
consequently influences the efficiency and the feasibility of the computation. Advances have
been made to find the resolution on the above-mentioned problems a posteriori error
estimation. Besides, the analyst can use a posteriori error estimates as an independent
measure of the quality of the simulation under study, whereby the computed solution itself is
used to assess the accuracy.
These are further differences between the a priori estimation of error and the a posteriori error
estimation. The a priori error estimates give information on the convergence and stability of
various solvers and can give rough information on the asymptotic behavior of errors in
calculations as mesh parameters are appropriately varied. A posteriori error estimation is much
more useful in computational mechanics and in solving partial differential equations. These are
typified by particular algorithms in which the difference in solutions obtained by schemes with
different orders of truncation error is used as a rough estimate of the error. Babuska and
Rheinboldt [19] started the modern definition of a posteriori error estimation for finite element
methods for two point elliptic boundary value problems. Techniques were developed that

11
delivered numbers ƞ 𝑘 approximating the error in an energy norm on each finite element K.
These formed the basis of adaptive meshing procedures designed to control and minimize the
error.
During the early 1980s several error estimators were introduced for effective adaptive
methods, of which many were based on a priori or interpolation estimates. They provided
crude but effective indications of the error, sufficient to derive adaptive processes. In the mean
time, Zienkiewicz and Zhu [27] developed a simple error estimation technique that is effective
for some classes of problems and types of finite element approximations. Their method is
categorized as a recovery-based method. Gradients of solutions obtained on a particular
partition are smoothed and then compared with the gradients of the original solution to assess
error. Eventually this approach evolved into the superconvergent patch recovery method. The
main scope of a posteriori estimator implementation for this work relies on SPR method, and it
has been expanded to estimate the local error in each element. The estimate is validated by the
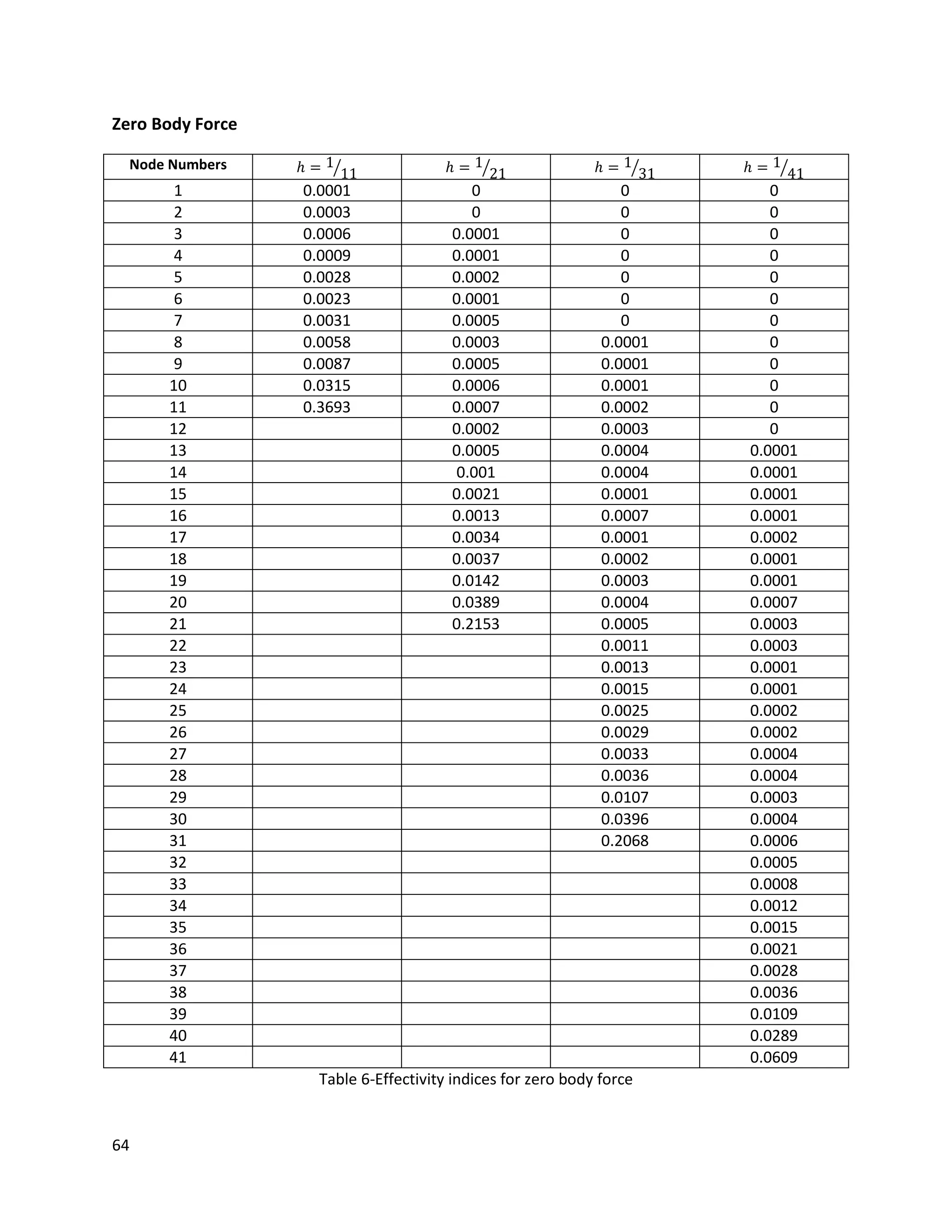
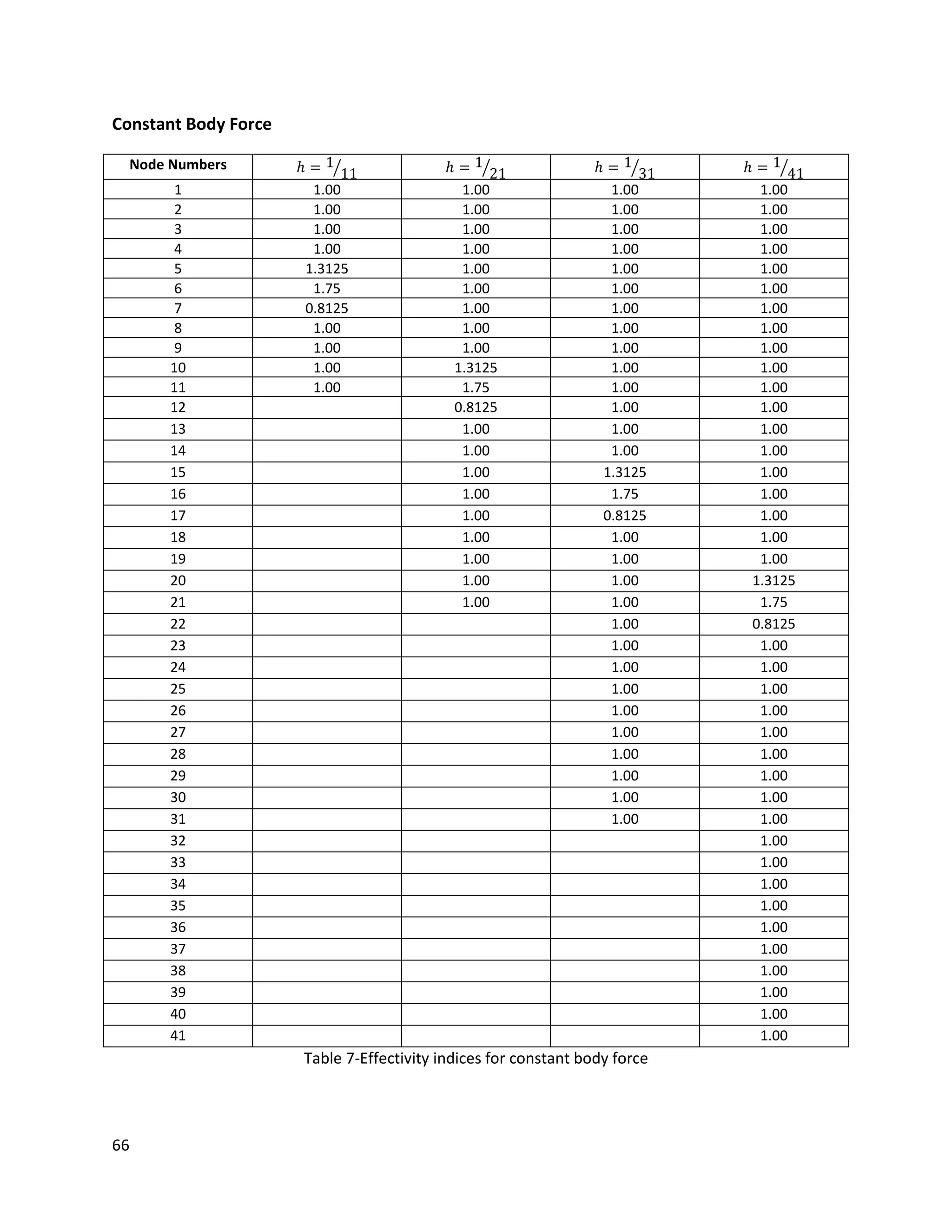
effectivity index for either one- or two-dimensional problem.
Extrapolation methods have been used effectively to obtain global error estimates for both the
h and p versions of finite element method [10]. Most studies have dealt with a posteriori error
estimation for the h version of the finite element method. However, the element residual
method is applicable to both p and h-p version finite element approximations. Generally, the
emphasis of a posteriori error estimation runs around the study of robustness of existing
estimators and indentifying limits on their performance. Generally, the main purpose of an
error estimator is to provide an estimate and ideally bounds for the solution error in a specified
norm or in a functional of interest. Some characteristics of an effective error estimator include:
 The error estimate should be accurate in the sense that the predicted error is close to
the actual (unknown) error.
 The error estimate should be asymptotically correct in the sense that with increasing
mesh density the error estimate should tend to zero at the same rate as the actual
error.
 Ideally, the error estimators should yield guaranteed and sharp upper and lower bounds
of the actual error.
 The error estimator should be computationally simple, with the error estimate (and
bounds) inexpensive to compute when measured on the total computations of the
analysis.
 The error estimator should be robust with regard to a wide range of applications,
including nonlinear analysis.

12
 The error estimator should make it possible to steer an adaptive refinement process
with error estimate used to optimize the mesh with respect to the global of the
computation.
However, the error estimator which would be able to satisfy all of these conditions is not
available yet. Even for linear problems, it is in general not possible to provide inexpensive
computable and guaranteed error bounds which are of practical interest. Of course, a key
requirement for the error estimator to be useful in engineering practice is that computational
cost of the error estimate must be much smaller than the added computational cost to simply
use a very fine mesh. The error estimates could be related to either the global bounds in energy
norms or theory of local estimates. The latter theory was extended to the local quantities of
interest that are crucial in applications. The work on local estimates has occurred with the
realization that the error at a particular point of interest in the domain can be polluted by
errors generated far outside the neighborhood of the point of interest.
1.4. Outline
An outline of the thesis is as follows. Chapter 2 examines the solution to a one-dimensional
model problem for interface problem with extended finite element method for different
enrichment function. Then, the a priori error estimators have been derived to estimate the
differences between the exact and approximated solution. The emphasis is on the computation
of L-2 norm and energy norm. In terms of a posteriori error estimation, the gradient based
recovery method is used to estimate the gradient of the exact solution. Chapter 3 introduces a
posteriori error estimation for interface in two-dimensional problem with extended finite
element method. In this problem, it is differentiated between the error blending and enriched
elements, by studying the effectivity index when various body forces are imposed.

13
2. One Dimensional Problem
2.1. Model Problem
2.1.1. Strong form
In this chapter, we describe the problem of one-dimensional linear elasticity for a bar of length
L, subjected to body force f(x), and traction F at x=L as shown in fig 1. The bar is clamped at the
left end (x=0). The scope of this model is to derive the exact displacement for the bar with two
different materials on both halves of the bar with a material interface in-between. Therefore,
the bar has been split up in two sub-elements, with cross sectional area and modulus of
elasticity 𝐴1and 𝐸1 for right hand side of bar, and for the left side 𝐴2 and 𝐸2. Here, the
eXtended Finite Element Method (X-FEM) is used to model the material interface without
remeshing.
Having stated the assumptions, the boundary value problem (BVP) which describes the
displacement of u(x) of the bar is given by
−(𝐸 𝑥 . 𝐴(𝑥). 𝑢,𝑥),𝑥 = 𝑓 in 𝛺 = (0, 𝐿) (1.1)
−𝐸 𝑥 . 𝐴(𝑥). 𝑢,𝑥 = 𝐹 (1.2)
𝑢 𝑥 = 0 = 0 (1.3)
where the comma denotes a derivative with respect to the variable denoted by the following
subscript. The derived strong form is valid for linear elasticity problem.
Figure 39-The one-dimensional model problem
We first derive the exact solution of the problem with assumption of elasticity material
properties behavior. The bar is under constant tension force and the body force is linearly
distributed along the bar and is given by the following equation:

14
𝑓 𝑥 = 2. 𝑥 (1.4)
If the cross section area for the first segment of bar is 1
2 and for the second part is 1, and the
module of elasticity along the bar is 1, then the exact solution is given by
𝑈 𝑥 =
2
3
∗ 𝑥3
0 < 𝑥 < 0.5 (1.5)
𝑈 𝑥 =
1
3
∗ 𝑥3
+
1
24
0.5 < 𝑥 < 1.0 (1.6)
Note that the displacement is continuous for each point along the bar.
2.1.2. Weak form and discrete system
Consider the static response of elastic bar of two different cross sections such as shown in
fig1. The strong form (2.1) sets in body 𝛺 ∈ ℝ3
with boundary Ƭ is given as:
𝑑
𝑑𝑥
𝐸 𝑥 𝐴 𝑥
𝑑𝑢
𝑑𝑥
+ 𝑓 = 0 𝑜𝑛 0 < 𝑥 < 𝑙 (1.7)
As it has been described before, the investigated problem contains the constant module
elasticity; as well as two different cross sectional area joined in the interface location known
as notation of 𝐴1 and 𝐴2 for right and left hand side of interface location, respectively. The
strong form can be developed into the finite element equations by restating the partial
differential equation in an integral form called the weak form (principle of virtual work). To
show how the weak form is developed, the previous strong form equation (2.7) is multiplied
by a weight or test function 𝑤(𝑥) and integrating over the whole domain which is the
interval [0, 𝑙].
𝑤
𝑑
𝑑𝑥
𝐸𝐴(𝑥)
𝑑𝑢
𝑑𝑥
𝑑𝑥 + 𝑤𝑓 𝑑𝑥 = 0
𝑙
0
𝑙
0
∀𝑤 ∈ 𝛺 𝑕 (1.8)
where 𝑢 𝑥 ∈ 𝛺 𝑕
and 𝑤 ∈ 𝛺 𝑕
are the approximating trial and test functions used in XFEM.
The 𝛺 𝑕
contains both the enriched and standard finite element space that the trial function
must satisfy the essential boundary condition, and which include the shape functions that
are discontinuous across the interface location.
To obtain the weak form, we take the advantage of integration by parts for the first
component of equation (2.8) to relate the strong form to the weak form. By the application
of integration by parts the first component of formula (2.8) is expanded and written as:

15
𝑤
𝑑
𝑑𝑥
𝐴 𝑥 𝐸
𝑑𝑢
𝑑𝑥
𝑑𝑥 = 𝑤𝐴 𝑥 𝐸
𝑑𝑢
𝑑𝑥
𝑙
0
𝑙
0
−
𝑑𝑤
𝑑𝑥
𝐴(𝑥)𝐸
𝑑𝑢
𝑑𝑥
𝑑𝑥
𝑙
0
(1.9)
Now with substitution of (2.9) into (2.8), it would be written as follows:
𝑤𝐴 𝑥 𝐸
𝑑𝑢
𝑑𝑥
𝑙
0
−
𝑑𝑤
𝑑𝑥
𝐴(𝑥)𝐸
𝑑𝑢
𝑑𝑥
𝑙
0
𝑙
0
(1.10)
The formula (2.10) could be written by expansion of the first term:
(𝑤𝐴2 𝐸
𝑑𝑢
𝑑𝑥
) 𝑥=𝑙 − (𝑤𝐴1 𝐸
𝑑𝑢
𝑑𝑥
) 𝑥=0 −
𝑑𝑤
𝑑𝑥
𝐴(𝑥)𝐸
𝑑𝑢
𝑑𝑥
𝑙
0
𝑙
0
(1.11)
The second term in the above vanishes because of the essential boundary condition. Also,
the (𝐴2 𝐸
𝑑𝑢
𝑑𝑥
) 𝑥=𝑙 stands as traction boundary condition. Therefore, the above equation
could be rewritten as follows:
𝑑𝑤
𝑑𝑥
𝐴(𝑥)𝐸
𝑑𝑢
𝑑𝑥
𝑙
0
𝑑𝑥 = (𝑤𝐴2 𝐸
𝑑𝑢
𝑑𝑥
) 𝑥=𝑙 + 𝑤𝑓 𝑑𝑥
𝑙
0
(1.12)
Because of the changing in cross sectional area of bar, the computation for the weak form is
broken up the general formulation of the weak form (2.8) into two compartments in
according to the location of interface. The weak form equation would be derived as
following equations: [put A = a1, a2]
𝑑𝑤
𝑑𝑥
𝑙
2
0
𝐴1. 𝐸
𝑑𝑢
𝑑𝑥
𝑑𝑥 = (𝑤𝐴1. 𝐸
𝑑𝑢
𝑑𝑥
) 𝑙
2
+
𝑤𝑙2
4
(1.13)
𝑑𝑤
𝑑𝑥
𝐴2. 𝐸
𝑑𝑢
𝑑𝑥
𝑑𝑥
𝑙
𝑙
2
= (𝑤𝐴2 𝐸
𝑑𝑢
𝑑𝑥
)𝑙 − (𝑤𝐴2 𝐸
𝑑𝑢
𝑑𝑥
) 𝑙
2
+
3𝑙2
4
𝑤 (1.14)
2.2. Finite Element Solution
The basic characteristic of finite element procedure is determined by the basis functions;
particularly their piecewise smoothness and local support of at least degree 1. In the global
point of view, these basis functions are considered to be defined everywhere on the domain of
the boundary-value problem. The global coordinates are useful in establishing the
mathematical properties of the finite element method. However, the computer

16
implementation is being carried out on a reference element which is determined by local
coordinates.
The approximated solution 𝑢 𝑕
is obtained by Galerkin method as a Variational Boundary Value
Problem (VBVP) restricted to the local domain. Each local domain is constructed by partitioning
of the global domain Ω into a set of m subdomains, labeled elements in fig…. Nodes are then
placed at the vertex of each element, for a total of n nodes in the domain. The coordinates of
the nodes are denoted by 𝑥1, 𝑥2, … , 𝑥 𝑛 and the element domains are denoted by 𝛺1, 𝛺2, … , 𝛺 𝑚 .
Associated with each node is a shape function 𝑁𝑖 or 𝛷𝑖, with compact support 𝜔𝑖. The support
of the nodal function is defined to be the union of the elements connected to the node. Fig 2
shows a nodal shape function and its support on a typical one- dimensional mesh.
Figure 40-A typical one-dimensional mesh of 4 elements. A linear shape function in corresponding to node 3 with support of
shape function [1].
The finite element approximation in the global domain reads
𝑢 𝑕
𝑥 = 𝑁𝑖(𝑥)𝑢𝑖
𝑛
𝑖=1
(1.15)
We can write the following properties:
 The approximation 𝑢 𝑕
interpolates the values 𝑢𝑖 of 𝑢 at nodes, i.e 𝑢 𝑕
𝑥𝑖 = 𝑢𝑖 = 𝑢(𝑥𝑖)
 The approximation is continuous, 𝑢 𝑕
∈ 𝐶0(𝛺)
 The approximation is exact for linear functions.
The interpolation property gives the physical meaning to the nodal coefficients 𝑢𝑖 as precisely
the values of the displacement field at the nodes. We shall provide a relation between the
domains of the global and local coordinates by linear function ξ : [𝑥 𝐴, 𝑥 𝐴+1] [𝜉1, 𝜉2], which
satisfies ξ(𝑥 𝐴)=𝜉1 and ξ(𝑥 𝐴+1)=𝜉2. It is standard practice to take 𝜉1=-1 and 𝜉2=+1. The local and
global descriptions of the eth element are depicted in fig 3.

17
Figure 41-Interpolation between local and global coordinate system [2].
The linear order of the approximation comes with the fact that the shape functions satisfy
𝑁𝑖
𝑖
𝑥 = 1 (1.16)
𝑁𝑖 𝑥 𝑥𝑖 = 𝑥
𝑖
(1.17)
Hence, if the nodal values are prescribed for an arbitrary linear field, the finite element
approximation reproduces the field exactly. The above equations are indicating the reproducing
condition, with the first implying that shape functions form a partition of unity. This property
corresponds to the ability of the approximation to represent rigid body modes, and is closely
tied to the convergence of the method.
Concerning the construction of the stiffness matrix K and the force vector F, the integral over
the domain Ω (integration over all elements) are replaced by a sum of integrals over each

18
element subdomain 𝛺𝑖. The polynomial characteristic of shape functions makes exact
integration possible. There are several other approaches for computation of the integrals, such
as the Gauss quadrature method. The evaluation of force vector F depends on the form of body
force and exerted loads. For this study case, we consider a linear body force along the element
and a pointed load at the end of the element, respectively.
We now consider the approximate finite element solution to the model BVP. The data are taken
to be the length of bar (L) = 1.0, the external force (𝐹𝑒𝑥𝑡 ) = 1.0. Initially the bar is refined into 10
elements, evenly spaced on the domain (0,1). At the end of this chapter the comparison figures
between the exact solution and FEM approximated solution are depicted. However, it should
be noted that in middle point of bar at X=0.5 there is a significant discrepancy between the
displacement of exact solution and traditional FEM approximation owning to the existence of a
material interface at this coordinate. Because of the disability of the traditional FEM to capture
either strong or weak discontinuity without remeshing, we used one of the enrichment
methods to avert the extra effort of refining the mesh, and hence being able to reach the
acceptable accuracy in the approximated solution. Thus, one scope of this project is to
implement the XFEM enrichment functions for weak discontinuities.
The physical problem, which is investigated in this thesis, is solid-solid interface problem. The
discontinuous element is enriched with the new function through a partition of unity. These
new functions are chosen a priori by the knowledge of the physical problem at hand. The
matter of choosing the enriched functions is elaborated in the description of code
implementation subroutines. The coordinate of the discontinuity is tracked by using a level set
function. Moreover, level set functions provide a natural choice for some enrichment functions
associated with discontinuous derivatives and discontinuous fields and can often be used
conventionally to compute other, more general, enrichment functions.
In 1-Dimensional code, the level set function has been implemented in a subroutine called
interface(x) that implements the linear geometrical function related to the interface position. It
comes with the equation of
𝛷 𝑥 = 𝑥 − 0.5 (1.18)
where x stands as current location of node along the domain.
As it can be perceived from upper equation, the interface function defines the position of
current node in according to interface coordination by its arithmetic sign:
Φ(x) < 0 left side of interface coordination
Φ(x) = 0 exact at interface coordination

19
Φ(x) > 0 right side of interface coordination
For each node 2 degree of freedom are allocated. One is dedicated to standard finite element
method, while the other one is spared to be implied for element with discontinuity.
In this code the basic idea of XFEM is implemented with several types of enriched shape
functions. These functions are built as the product of global enrichment functions with some
finite element shape functions. The point x is taken as an arbitrary value in the finite element e.
Denote the element’s nodal set as 𝑁𝑒 = {𝑛1 , 𝑛2 , … , 𝑛 𝑚 𝑒
}, where 𝑚 𝑒 is the number of nodes of
element e. The enriched displacement approximation for a vector-valued function 𝒖 𝑕
∶ 𝑅 𝑑
→
𝑅 𝑑
is of the form
𝑢 𝑕
= 𝑁𝐼
𝐼∈𝑁 𝑒
𝑥 𝑢𝐼 + 𝑁𝐽
𝐽∈𝑁 𝑒𝑛𝑟
𝑥 𝛹(𝑥)𝑎𝐽 (1.19)
Where the 𝑁 𝑒𝑛𝑟
is set of nodes whose support is cut by discontinuity, and 𝑁𝑒 is set of nodes
that are not enriched. 𝑁𝐼 and 𝑁𝐽 are finite element shape functions. The choice of enriched
function (Ψ(x)) depends on a priori solution of the problem. The 𝑢𝐼 is the nodal unknown as
well as 𝑎𝐽 for standard finite elements and enriched elements, respectively. 5 different types of
these functions have been implemented in this code, and subsequently the intrinsic estimated
error for each approximated solution is compared.
Moreover, for those enriched shape functions that brings an additional term in approximated
solution, the enriched function is shifted according to the value of the enriched function in
corresponding node. The modified approximation becomes:
𝒖 𝑕
= 𝑁𝐼
𝐼∈𝑁 𝑒
𝑥 𝒖𝐼 + 𝑁𝐽
𝐽∈𝑁 𝑒𝑛𝑟
𝑥 (𝛹 𝑥 − 𝛹 𝑥𝐽 )𝑎𝐽 (1.20)
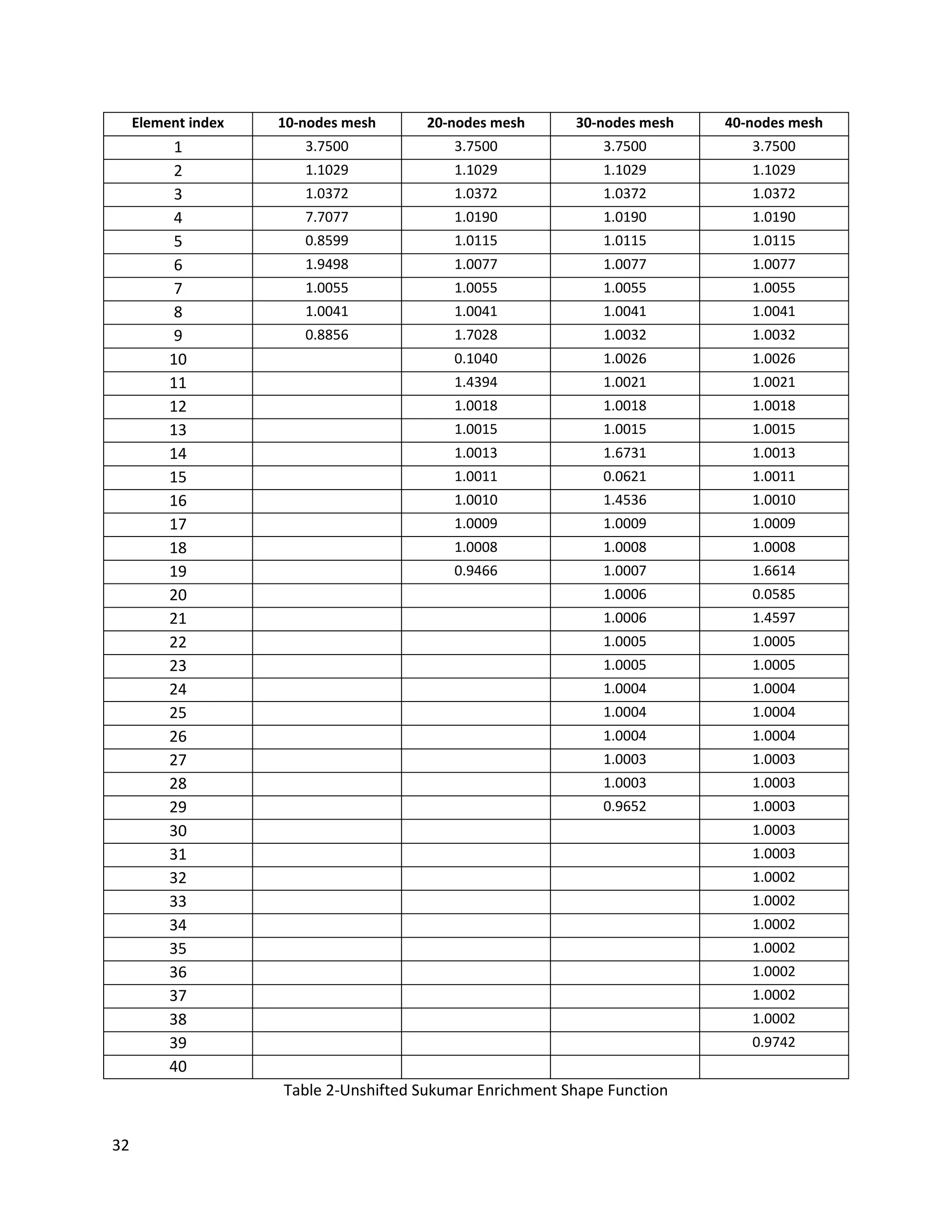
The first choice of enriched shape function is suggested by Sukumar [24], known as the signed
distance shape function. The second type is shifted version of this enrichment. The equation for
Sukumar enrichment is
𝛹 𝑥 = 𝛷(𝑥) (1.21)
and the shifted enrichment is
𝛹 𝑥 = 𝛷(𝑥) − 𝛷(𝑥𝑖) (1.22)
Both of these enriched shape function however, lead to issues with the blending between the
enriched and unenriched elements. The existence of blending elements imposes extra error in

20
approximated solution, as a result deteriorate the convergence rate. It all comes through two
main properties of blending elements: i) In these elements, the enrichment function can no
longer be reproduced exactly (because of a lack of a partition of unity). ii) These elements
produce unwanted terms into the approximation which cannot be compensated by standard FE
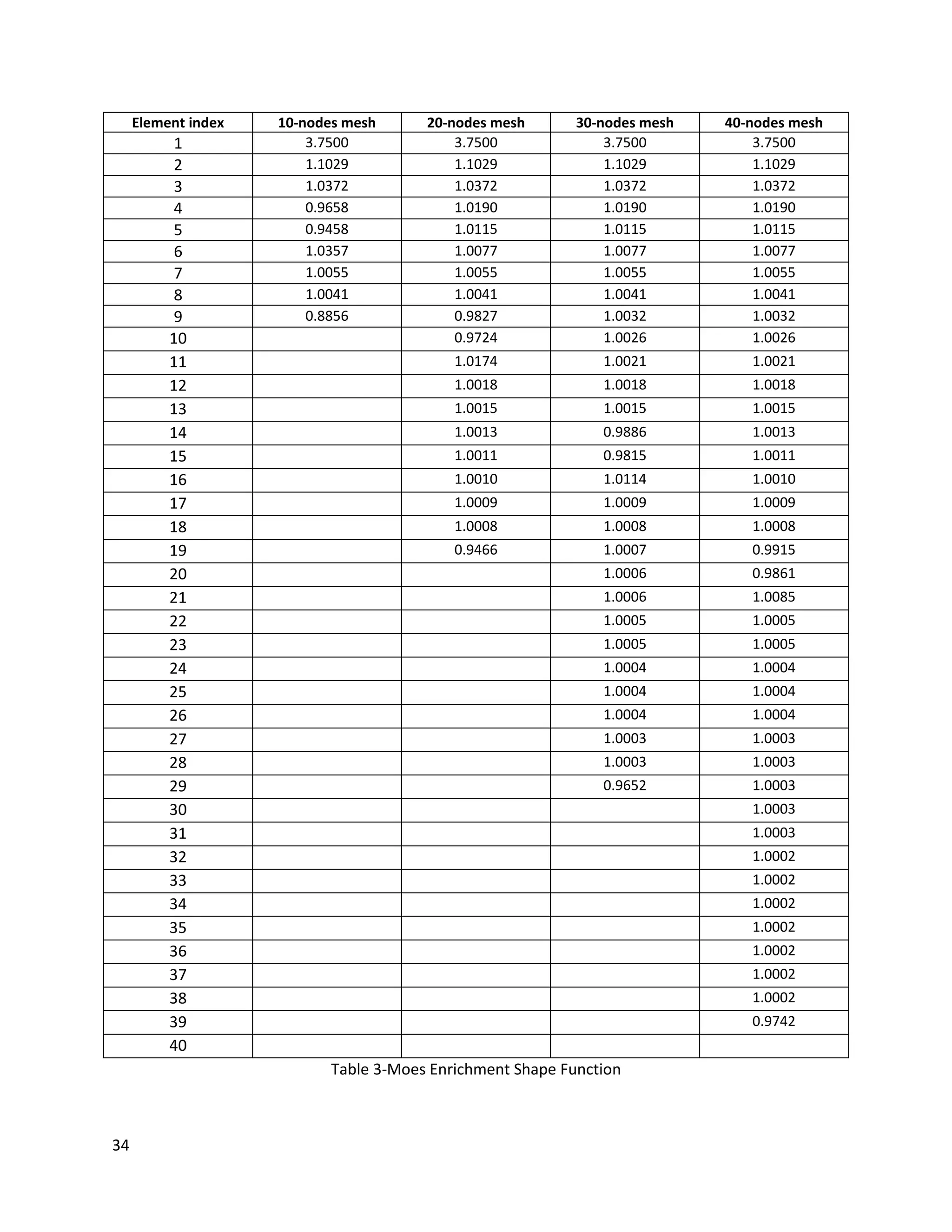
part of the approximation. Hence, Prof. Moes [4] and his co-workers used a new enriched
shape function which is able to eliminate the problems in the blending elements with the
enhancement of geometrical configuration and extra degree of freedom. The modified
equation of this enriched function is given by an interpolation of nodal values minus the
absolute value of the common ramp function, illustrated as:
𝛹 𝑥 = 𝑁. 𝛷(𝑥𝑖) − 𝛷(𝑥) (1.23)
where N denotes to standard shape function.
As could be perceived at the end of this chapter, this enriched shape function leads to the most
optimal enrichment among the other implemented enriched shape functions.
Another special treatment was proposed to eliminate the unwanted terms by Prof.Fries [3].
This new approached is known as modified or corrected XFEM, whereas the original definition
is called standard XFEM. Two significant differences can be found in the approximation of the
standard and corrected XFEM: i) In addition to those nodes that are enriched in the standard
XFEM, all nodes in the blending elements are enriched. That is, a complete partition of unity is
present in the reproducing and blending elements. ii) The enrichment functions of the standard
XFEM are modified except in the reproducing elements. These are element with all nodes being
enriched that are capable of reproducing the enriched function exactly. The enrichment
functions are zero in the standard FEs, and in the blending elements, they are multiplied by a
function that varies continuously between 0 and 1.(also called a ramp function) With the aid of
corrected XFEM there are no more unwanted terms in the blending elements.
The modified enrichment function is defined with 𝛹 𝑚𝑜𝑑
(x) as
𝛹 𝑚𝑜𝑑
𝑥 = 𝛹 𝑥 . 𝑅(𝑥) (1.24)
With R(x) being a ramp function
𝑅 𝑥 = 𝑁𝑗 (𝑥)
𝑗∈𝑁 𝑒𝑛𝑟
(1.25)

21
It is obvious that 𝛹 𝑚𝑜𝑑
(x) = Ψ(x) in the reproducing elements. Furthermore, 𝛹 𝑚𝑜𝑑
(x) = 0 in the
standard FEs. In the blending elements, the modified enrichment function 𝛹 𝑚𝑜𝑑
(x) varies
continuously between Ψ(x) and zero. There, due to multiplication with R(x), the order of
𝛹 𝑚𝑜𝑑
(x) is increased when compared with Ψ(x), and slightly more integration points may be
needed for the integration.
A nodal subset 𝑁 𝑚𝑜𝑑
⊂ 𝑁 𝑒
is introduced, which consists of all element nodes of the
reproducing and blending elements. The enriched shape functions are now defined as
𝑀 𝑚𝑜𝑑
= 𝑁𝑗 𝑥 . 𝛹 𝑚𝑜𝑑
(𝑥) (1.26)
The following modified approximation is used in the proposed corrected XFEM:
𝑢 𝑕
𝑥 = 𝑁𝑖
𝑖∈𝑁 𝑒
𝑥 . 𝑢𝑖 + 𝑀𝑖
𝑚𝑜𝑑
𝑥 .
𝑖∈𝑁 𝑚𝑜𝑑
𝑎𝑖 (1.27)
The corrected XFEM possesses the following properties:
 All nodes that belong to modified elements domain (𝑀 𝑚𝑜𝑑
) are enriched in the
proposed XFEM approximation, whereas only nodes in the reproducing elements are
enriched in the standard XFEM approximation. Therefore, there are more unknowns
resulting from the proposed version.
 In the proposed version of XFEM, the enrichment function 𝛹 𝑚𝑜𝑑
(𝑥) is used instead of
Ψ(x).
 The modified enrichment function 𝛹 𝑚𝑜𝑑
𝑥 is non-zero only in the reproducing and
blending elements. Most importantly, it would return the zero in elements with only
some of their nodes in the modified elements domain. That is, no unwanted terms are
introduced by the proposed XFEM approximation, and therefore, there is no need for
any special treatment in the blending elements. By contrast, in the standard XFEM
approximation, the enrichment function Ψ(x) is non-zero in the blending elements.
 In the proposed XFEM approximation, 𝑁𝑗 𝑥 form a partition of unity in the
reproducing and blending elements. Consequently, the modified enrichment function
𝛹 𝑚𝑜𝑑
𝑥 can be reproduced exactly in all elements where this function is non-zero. In
the standard XFEM, however, the enriched function Ψ(x) can be reproduced exactly only
in the reproducing elements but not in the blending elements.
This enriched shape function should be shifted at the corresponding node by the value at
the node for reaching to more accuracy in modified elements. The modified enriched
formulation is changed to:

22
𝛹 𝑚𝑜𝑑
x = 𝛹 𝑥 − 𝛹 𝑥𝑖 . 𝑅 𝑥 (1.28)
This enriched function is used for the general approximation equation. Moreover, it could
be seen at the end of this chapter the approximation error of each approach, according to
representation of the error estimated figures and tables, then from there easily could be
seen the best option of enriched shape function to be opted for further conduction of
research.
2.3. Error Estimator
Mainly, the gradient of the approximation is of interest for engineers. However, the
gradient of the approximation is generally discontinuous over the element boundaries,
meaning that regardless of the continuity of the main quantity of interest, its gradient
would be discontinuous. Thus, many finite element programs incorporate a post-processing
procedure whereby the discontinuous approximation to the gradient is smoothed before
being presented to the user. The post-process applies on the approximation 𝑢 𝑥 to obtain
more accurate representations of the gradient 𝐺(𝑢 𝑥). One can then use the difference
𝐺 𝑢 𝑥 − ∇𝑢 𝑥 as an estimate for the error. One of the weakness of the method and at the
same time, one of its advantages, is that no use is made of the information from the exact
solution.
The graphical representation of the gradient of approximation is not the only reason for the
post-processing procedure. It is also found that the accuracy of the smoothed gradient is
superior to the approximation provided by the untreated gradient of the original finite
element approximation. A rather natural approach to a posteriori error estimation is based
on measuring the difference between the direct and post-processed approximations to the
gradient. In order to explain the definition of a posteriori error estimation, we will first
define two ways of measuring errors in the finite element approximation. The 𝐿2
Norm is
the one that stands as subtraction of exact and analytical computed solution. The 𝐿2
Norm
error is calculated for each element, then it can be summed over all elements in a body of
the domain. An a priori error estimator in 𝐿2
norm for the finite element approximation 𝑢 𝑕
is:
𝑢 − 𝑢 𝑕 𝐿2
2
= ( 𝑢 − 𝑢 𝑕
2
𝑑𝑥) ≤ 𝐶𝑕 𝑃+1
𝑢 𝑃+1
(1.29)
where P is the degree of piecewise polynomial shape functions and u(x) is smooth solution. h is
the diameter of the largest element.

23
In order to calculate the energy norm, the gradient of both true and approximated solution is
considered. An a priori error estimator in energy norm is:
𝑢 − 𝑢 𝑕 𝐸
2
= ∇𝑢 − ∇𝑢 𝑕
2
𝑑𝑥 ≤ 𝐶𝑕 𝑝
𝑢 𝑃+1
(1.30)
As it could be seen from two former equations, the accuracy of the approximation in 𝐿2
norm is
one power of h higher than energy norm of the error. The estimation of the error depends on
the unknown constant e and the term 𝑢 𝑃+1 which in general is also not known. To get an
error estimator that does not depend on unknown constants, we need to study a posteriori
error estimators, which are based on the approximated solution itself.
A reasonable a posteriori error estimator can be obtained by using a suitable approximation to
the gradient in place of ∇𝑢. In particular, the gradient of the exact solution could be
approximated by a suitable post-processing of the finite element approximation, denoted by
𝐺 𝑕[𝑢 𝑕].
The a posteriori error estimator is then simply taken as
ƞ2
= 𝐺 𝑕 − ∇𝑢 𝑕
2
𝑑𝑥 (1.31)
This approach allows considerable leeway in the selection of the post-processed gradient, as it
has already been mentioned the gradient of the finite element approximation provides a
discontinuous approximation to the true gradient. One possible approach that overcomes this
problem is the use of averaging methods. The idea is to construct an approximation at each
node by averaging the contribution from each of the elements surrounding the node. These
values may then be interpolated to obtain a continuous approximation over the whole domain.
The specific steps used to construct the averaged gradient at the nodes distinguish the various
estimators and have a major influence on the accuracy and robustness of the resulting
estimator. The several available rigorous approaches for computation of estimators lay within
the framework of corresponding to a particular recovered gradient 𝐺𝑥.
The implementation of the gradient recovery will be elaborated in several steps. The first step is
to define the procedure for smoothing the gradient of the finite element approximation. The
recovered gradient is denoted by 𝐺 𝑕(𝑢 𝑕), where 𝑢 𝑕 is the finite element approximation. The
recovered gradient is itself piecewise linear, with values at the nodes obtained by first
interpolating the gradient of the finite element approximation at the centroids of the elements
sharing the node. In each element 𝐾 the estimator is defined as

24
ƞ 𝑘 = 𝐺 𝑕 𝑢 𝑕 − 𝑢 𝑕
′
𝐿2 𝐾 (1.32)
The main ingredient in deriving the estimator centers on the construction of recovery operator
𝐺𝑥. There is a significant reason for seeking a recovered gradient in the form of a piecewise
linear function, besides that one of convenience. Specifically, the finite element approximation
is itself piecewise linear, meaning that the same numerical procedures already present in the
finite element code may be reused to store and handle the post-processed gradient.
The reason for collecting the gradient at the centroid of the elements is related to the well
known fact that the gradient at the centroids is more accurate (or superconvergent). It is
natural to use the gradient sampled at these points to produce an accurate post-processed
gradient. If 𝑢 ∈ 𝐻3
(𝛺) and the partition is uniform, then
𝑢 𝑥 − 𝐼𝑥 𝑢 𝐻1(𝛺) ≤ 𝐶𝑕2
|𝑢| 𝐻3(𝛺) (1.33)
Where 𝐼 is the FEM-interpolant, 𝐻1
𝛺 and 𝐻3
(𝛺) are first and third derivation of Hilbert
space. The accuracy of piecewise linear finite elements measured in the energy norm is known
to be O(h). As a result, the recovered solution is a better approximation to the exact solution
than the finite element solution. The recovery operator obtained by interpolating the solution
values at the centroids of the elements, satisfies the following condition
𝐺 𝑕 𝐼𝑕 = 𝐼𝑕 𝑣′
= 𝑣′
∀ 𝑣 ∈ ℙ2 (1.34)
The above identity shows that the recovered gradient 𝑣′
obtained by linear interpolation of the
values at the centroids, it is equal the actual gradient for quadratic polynomials. This
observation leads to the condition that the approximation
𝐺 𝑕 𝑢 𝑕 ≈ 𝑢′ (1.35)
is itself superconvergent. The global estimator is obtained by summing the contributions from
each element. The recovery-based estimator will give an asymptotically exact estimate of the
true error if the superconvergence property is present. In particular, let ƞ be the a posteriori
estimator and ||e|| be the true energy norm error, then ƞ is asymptotically exact if
lim
𝑕→0
ƞ
| 𝑒 |
= 1 (1.36)
This indicates that the problem of finding a posteriori error estimator is related to the
construction of an appropriate recovery operator 𝐺𝑥.

25
The quality of an estimator is often judged by global effectivity indices
𝜃 =
ƞ
𝑒
or local effectivity indices
𝜃 𝑘 =
ƞ 𝑘
ƞ 𝑘
These indices can be used to measure the quality of an estimator when the exact error or a
good approximation of it are known. The comprehension of previous concepts gives the rule of
the error estimator implementation for post-processing finite element belonged to one
dimensional problem code. Its whole orientation can be summarized in following figure:
Figure 42-Construction of recovery operator 𝑮 𝒉 from piecewise linear approximation in one dimension [9].

26
2.4. Implementation and Results-1D
In this section, the outcomes of implementation would be illustrated both in graphs and tables,
and it also would be accompanied with the general outline of code and how the digits are
demonstrating the effictivity indices for each time of implementation process.
The first implementation goes around the enriched shape function of Sukumar (1.13-1.14) in
either case, shifted and unshifted. For each it is considered 5 number of Gauss points, two
degree of freedoms is assigned per node. The unit value of external force is exerted at the end
of bar plus distributed body force which has been explained at first subsection of this chapter.
At the beginning, the whole domain is subdivided evenly with specification number of 10
nodes, and then it is increased to 20, 30, and at last to 40 nodes. Afterwards, the effictivity
indices are compared for each time of refinements till it turns to be obvious that with each time
refinement the error also declines to stand in proximity of one.
The representation of output data is sorted out in the way that for each time refinement, the
displayed graphs are solely stood to be justified the behavior of the results after for next step of
refinement. The effictivity indices for each corresponding nodes in each time analysis are
shown all in the table with respect to current implemented enrichment shape function.
In order to perform each of implemented enrichment shape function to gain new result of error
estimator, the subroutine EnrichmentFunction is called to bring back the effect of the related
enrichment shape function on the main calculation of estimated error. The subroutine
GrRecdUh allocates the linear interpolation of strain at the superconvergence point ensuing to
the described governing rules for computation of strains with aid of superconvergence
property. The superconvergence coordination is determined in subroutine main then the
strains at superconvergence points for each element, which comes out from the number of
rows in connectivity matrix, is calculated as derivative of approximated displacement. As it has
already been explained, the ratio of effictivity index requires two components of error as
gradient recovery error and energy norm in upper and downer part of ratio respectively. The
computation of either of those errors is carried out in two different subroutines with aim on
Gauss quadrature integration theory for local element named as EnergynormEnr and
GradientrecoverynormEnr. Afterwards, each output data value of error goes through a loop
over whole elements domain to end up the global error.
The representation graphs draw the differentiation between two different computed errors as
one depicting the subtraction of the derivative of the exact and approximated displacements
and another one the gradient of recovery solutions versus the analytical displacements. For
each time refinement, the effictivity indices and relative graphs could be fine with respect to
opted enrichment shape function. The first beginning one stands for shifted Sukumar

27
enrichment function. As it can be seen, the kink in displacement results in distortion for
enriched element and in its proximity for blending elements. Also, the effect of the applied
enrichment function could not be neglected in the intensity of fluctuation for corresponding
elements.

28
Element index 10-node mesh 20-node mesh 30-node mesh 40-node mesh
1 3.7500 3.7500 3.7500 3.7500
2 1.1029 1.1029 1.1029 1.1029
3 1.0372 1.0372 1.0372 1.0372
4 7.7077 1.0190 1.0190 1.0190
5 0.8599 1.0115 1.0115 1.0115
6 1.9498 1.0077 1.0077 1.0077
7 1.0055 1.0055 1.0055 1.0055
8 1.0041 1.0041 1.0041 1.0041
9 0.8856 1.7028 1.0032 1.0032
10 0.1040 1.0026 1.0026
11 1.4394 1.0021 1.0021
12 1.0018 1.0018 1.0018
13 1.0015 1.0015 1.0015
14 1.0013 1.6731 1.0013
15 1.0011 0.0621 1.0011
16 1.0010 1.4536 1.0010
17 1.0009 1.0009 1.0009
18 1.0008 1.0008 1.0008
19 0.9466 1.0007 1.6614
20 1.0006 0.0585
21 1.0006 1.4597
22 1.0005 1.0005
23 1.0005 1.0005
24 1.0004 1.0004
25 1.0004 1.0004
26 1.0004 1.0004
27 1.0003 1.0003
28 1.0003 1.0003
29 0.9652 1.0003
30 1.0003
31 1.0003
32 1.0002
33 1.0002
34 1.0002
35 1.0002
36 1.0002
37 1.0002
38 1.0002
39 0.9742
40
Table 1-Shifted Sukumar Enrichment Shape Function

29
10 nodes:
Figure 43-Error graphs for shifted Sukumar enrichment function, 10 nodes
20 nodes:
30 nodes:

30
40 nodes:
In terms of unshifted Sukumar enriched shape function, the next implementation is carried out
for the same assumption of input values. So, the aim of this implementation could be rolled on
the influence of shifting for enrichment shape function. The order of graphs and the effictivity
indices would count for true comparison on account of modification in enrichment shape
function.
10 nodes:
Figure 47-Error graphs for Unshifted Sukumar enrichment function, 10 nodes

31
20 nodes:
30 nodes:
40 nodes:

32
Element index 10-nodes mesh 20-nodes mesh 30-nodes mesh 40-nodes mesh
1 3.7500 3.7500 3.7500 3.7500
2 1.1029 1.1029 1.1029 1.1029
3 1.0372 1.0372 1.0372 1.0372
4 7.7077 1.0190 1.0190 1.0190
5 0.8599 1.0115 1.0115 1.0115
6 1.9498 1.0077 1.0077 1.0077
7 1.0055 1.0055 1.0055 1.0055
8 1.0041 1.0041 1.0041 1.0041
9 0.8856 1.7028 1.0032 1.0032
10 0.1040 1.0026 1.0026
11 1.4394 1.0021 1.0021
12 1.0018 1.0018 1.0018
13 1.0015 1.0015 1.0015
14 1.0013 1.6731 1.0013
15 1.0011 0.0621 1.0011
16 1.0010 1.4536 1.0010
17 1.0009 1.0009 1.0009
18 1.0008 1.0008 1.0008
19 0.9466 1.0007 1.6614
20 1.0006 0.0585
21 1.0006 1.4597
22 1.0005 1.0005
23 1.0005 1.0005
24 1.0004 1.0004
25 1.0004 1.0004
26 1.0004 1.0004
27 1.0003 1.0003
28 1.0003 1.0003
29 0.9652 1.0003
30 1.0003
31 1.0003
32 1.0002
33 1.0002
34 1.0002
35 1.0002
36 1.0002
37 1.0002
38 1.0002
39 0.9742
40
Table 2-Unshifted Sukumar Enrichment Shape Function

33
Moes Enrichment Shape Function:
The outputs and results analysis of Moes enrichment shape function would be illustrated for
four different numbers of refinements. All input values are set in the same orientation of
previous analysis. The analysis starts with 10 nodes number as refinement, similarly as before
the analysis was conducted in four times refinement as tenfold.
The characteristic of this function causes Moes function to become well known as one of the
best enrichment shape function that is able to cover the discontinuity in continuum mechanics
domain with fairly approximated solution close to the exact one. The effectivity indices of the
next table put a proof on the fact that the Moes function is one the best applicable enrichment
shape function in XFEM analysis.

34
1 3.7500 3.7500 3.7500 3.7500
2 1.1029 1.1029 1.1029 1.1029
3 1.0372 1.0372 1.0372 1.0372
4 0.9658 1.0190 1.0190 1.0190
5 0.9458 1.0115 1.0115 1.0115
6 1.0357 1.0077 1.0077 1.0077
7 1.0055 1.0055 1.0055 1.0055
8 1.0041 1.0041 1.0041 1.0041
9 0.8856 0.9827 1.0032 1.0032
10 0.9724 1.0026 1.0026
11 1.0174 1.0021 1.0021
12 1.0018 1.0018 1.0018
13 1.0015 1.0015 1.0015
14 1.0013 0.9886 1.0013
15 1.0011 0.9815 1.0011
16 1.0010 1.0114 1.0010
17 1.0009 1.0009 1.0009
18 1.0008 1.0008 1.0008
19 0.9466 1.0007 0.9915
20 1.0006 0.9861
21 1.0006 1.0085
22 1.0005 1.0005
23 1.0005 1.0005
24 1.0004 1.0004
25 1.0004 1.0004
26 1.0004 1.0004
27 1.0003 1.0003
28 1.0003 1.0003
29 0.9652 1.0003
30 1.0003
31 1.0003
32 1.0002
33 1.0002
34 1.0002
35 1.0002
36 1.0002
37 1.0002
38 1.0002
39 0.9742
40
Table 3-Moes Enrichment Shape Function

35
10 nodes:
Figure 51-Error graphs for Moes enrichment function, 10 nodes
20 nodes:
30 nodes:

36
40 nodes:
The Fries enrichment shape function as well as Sukumar is once implemented for unshifted
function and then it is shifted for next step of analysis. Again, all assumption input values go the
same for both of upcoming analysis.
With comparison of effectivity indices table of both shifted and unshifted Fires function, it
could be conceived the significant influence of the elimination extra node values except for
enriched node in the reduction of error computation. In the contrariwise to Sukumar function,
the shifted Fries enrichment function makes the magnificent contribution in the improvement
of the output quantitative results, and all is occurred due to the advantage of blending
elements elimination.

37
1 3.7500 3.7500 3.7500 3.7500
2 1.1029 1.1029 1.1029 1.1029
3 1.0308 1.0372 1.0372 1.0372
4 15.0049 1.0190 1.0190 1.0190
5 0.9418 1.0115 1.0115 1.0115
6 2.9782 1.0077 1.0077 1.0077
7 0.9937 1.0055 1.0055 1.0055
8 1.0041 0.8510 1.0041 1.0041
9 0.8856 1.4634 1.0032 1.0032
10 0.9075 1.0026 1.0026
11 1.4424 1.0021 1.0021
12 0.8183 1.0018 1.0018
13 1.0015 0.7413 1.0015
14 1.0013 1.5263 1.0013
15 1.0011 0.6964 1.0011
16 1.0010 1.4084 1.0010
17 1.0009 0.6730 1.0009
18 1.0008 1.0008 0.6540
19 0.9466 1.0007 1.5380
20 1.0006 0.5379
21 1.0006 1.4005
22 1.0005 0.5732
23 1.0005 1.0005
24 1.0004 1.0004
25 1.0004 1.0004
26 1.0004 1.0004
27 1.0003 1.0003
28 1.0003 1.0003
29 0.9652 1.0003
30 1.0003
31 1.0003
32 1.0002
33 1.0002
34 1.0002
35 1.0002
36 1.0002
37 1.0002
38 1.0002
39 0.9742
40
Table 4-Unshifted Fries Enrichment Shape Function

38
10 nodes:
Figure 55-Error graphs for Unshifted Fries enrichment function, 10 nodes
20 nodes:
30 nodes:

39
40 nodes:
In the continuous of analysis with Fries function, the modification of this function with shifting
in according to the nodal value causes to diminish the side effect of the imposed error, flows
into the computation with unexpected terms in the nodes affected by Fries function. The
improvement could be seen in either next page effictivity indices or the value of error in the
graphs for each time refinement.

40
1 3.7500 3.7500 3.7500 3.7500
2 1.1029 1.1029 1.1029 1.1029
3 0.7932 1.0372 1.0372 1.0372
4 1.3774 1.0190 1.0190 1.0190
5 1.4025 1.0115 1.0115 1.0115
6 0.8942 1.0077 1.0077 1.0077
7 1.0041 1.0055 1.0055 1.0055
8 0.8856 0.8291 1.0041 1.0041
9 1.1331 1.0032 1.0032
10 1.4168 1.0026 1.0026
11 1.3233 1.0021 1.0021
12 0.8766 1.0018 1.0018
13 1.0015 0.8392 1.0015
14 1.0013 1.1714 1.0013
15 1.0011 1.4309 1.0011
16 1.0010 1.2955 1.0010
17 1.0009 0.8701 1.0009
18 1.0008 1.0008 0.8437
19 0.9466 1.0007 1.1891
20 1.0006 1.4381
21 1.0006 1.2812
22 1.0005 0.8667
23 1.0005 1.0005
24 1.0004 1.0004
25 1.0004 1.0004
26 1.0004 1.0004
27 1.0003 1.0003
28 1.0003 1.0003
29 0.9652 1.0003
30 1.0003
31 1.0003
32 1.0002
33 1.0002
34 1.0002
35 1.0002
36 1.0002
37 1.0002
38 1.0002
39 0.9742
40
Table 5-Shifted Fries enrichment shape function

41
10 nodes:
Figure 59-Error graphs for shifted Fries enrichment function, 10 nodes
20 nodes:
30 nodes:

42
40 nodes:
It can be concluded that among all prior enrichment shape functions, the Moes enrichment
shape function has proved that it would converge the more accurate output solution, it has
been shown based on the values of effictivity indices, rather than its other counterparts.

43
3. Two-Dimensional Problem
3.1. Model Problem:
Here in this section, the governing equation is derived out for linear elasto-statics stage in
continuum mechanics with assumption of zero, constant and linear distribution of body force.
Consider the domain Ω bounded by Ƭ. The boundary Ƭ is composed of the sets Ƭ 𝑢 and Ƭ𝑡 such
that Ƭ = Ƭ 𝑢 ∪ Ƭ𝑡 as shown in fig25 Prescribed displacements 𝑢 are imposed on Ƭ 𝑢 , while
tractions 𝑡 are imposed on Ƭ𝑡.
Figure 63-TWO-Dimensional Model Problem
The configuration of plate has been chosen to be square, and the interface coordination is
intersected in the middle of length side of plate. The plate is constrained in the bottom, and the
constant tensile force with value of 10 is exerted at the top of plate. For both materials the
Young’s modulus is considered equal to zero. Therefore, the plate would not deform in
opposite direction of applied load.
With assumption of being variable the cross sectional area and modulus of elasticity along the
domain, the equilibrium equations and boundary conditions are
−(𝐴(𝑥)𝐸(𝑥)𝑢,𝑥),𝑥 = 𝑓 (3.1)
−𝐴 𝑥 𝐸 𝑥 𝑢,𝑥 = 𝐹 (3.2)
𝑢 𝑥 = 0 = 0 (3.3)

44
where A(x) is standing as cross sectional area for plate which is constant all long way, so it could
be eliminated from deriving procedures of the governing equation. The f and F are the value of
body force and traction force, respectively. For the first equation, we assume the ignorance of
the body force existence in the domain, the equilibrium equation is calculated as
𝑢 𝑦 =
𝐹
𝐸2
∗ 𝑦 for 𝑦 at 𝐸2 (3.4)
𝑢 𝑦 =
𝐹
2 ∗ 𝐸2
+
𝐹
𝐸1
∗ 𝑦 − 0.5 for 𝑦 at 𝐸1 (3.5)
In terms of constant body force:
𝑢 𝑦 =
1
𝐸2
∗ −
𝑦2
2
+ 𝐹 + 1 ∗ 𝑦 for 𝑦 at 𝐸2 (3.6)
𝑢 𝑦 =
1
𝐸2
∗ −
1
8
+
1
2
∗ 𝐹 + 1 +
1
𝐸1
∗ −
𝑦2
2
+ 𝐹 + 1 ∗ 𝑦
+
1
8
−
1
2
∗ 𝐹 + 1 for 𝑦 at 𝐸1
(3.7)
With consideration of linear distributed body force
𝑓 = 𝑦 (3.8)
The equilibrium equations would be transformed to
𝑢 𝑦 =
1
𝐸2
∗ −
𝑦3
6
+
𝑦
2
+
𝐸1
𝐸2
∗ 𝐹 ∗ 𝑦 for 𝑦 at 𝐸2 (3.9)
𝑢 𝑦 =
1
𝐸2
∗ −
1
48
+
1
4
+
𝐸1
𝐸2
∗
𝐹
2
+
1
𝐸1
∗ −
𝑦3
6
+
𝑦
2
+ 𝐹 ∗ 𝑦 +
1
𝐸1
∗
1
48
−
1
4
−
𝐹
2
for 𝑦 at 𝐸1
(3.10)

45
3.2. Overview of MXFEM
The defined level set method makes it able for users to track the discontinuity or interface for a
closed or open section by defining sign distance values at discreet points in the domain of
interest. Each point is assigned a signed distance value from the points lied on the interface
denoted Ƭ. A continuous level set function Φ(x) is introduced where x is a point in the domain
of interest Ω. The level set function can be subdivided as a function of the domain and with a
time component as
𝛷 𝑥, 𝑡 < 0 𝑓𝑜𝑟 𝑥 ∈ 𝛺 (3.11)
𝛷 𝑥, 𝑡 > 0 𝑓𝑜𝑟 𝑥 ∉ 𝛺 (3.12)
𝛷 𝑥, 𝑡 = 0 𝑓𝑜𝑟 𝑥 ∈ Ƭ (3.13)
In according to above formulations, the value of the level set function at each point is updated
based on the front velocity for points lied in the domain using a finite difference technique to
approximate the solution to the governing partial differential equation. If the time step is small,
the finite difference method can provide sufficient accuracy. When the forward finite difference
technique is considered, the derivative of Φ with respect to time can be approximated as
𝛷𝑖+1 − 𝛷𝑖
∆𝑡
+ 𝑉𝑖. ∇𝛷𝑖 = 0 (3.14)
Where 𝛷𝑖+1 is updated level set value, 𝛷𝑖 is the current level set value, 𝑉𝑖 is the front velocity
vector, and ∆𝑡 is the elapsed time space between i and i+1. The time step ∆𝑡 is limited by the
Courant-Friedrichs-Lewy (CFL) condition which ensures that the approximation to the solution
of the partial differential equation converges.
To become able to imply the level set method for open sections, the modified version of level
set method was introduced which allows for open sections to be tracked with the use of
multiple level set functions. An open section should be described by two level sets Φ(x) and
Ψ(x). Also, both functions could represent the growth rate of discontinuity via variable of time.
One sample of sign distance function is illustrated as a level set method for an open section in
fig… It should be noted that the interface of interest is given as the region where phi is negative
and psi is equal to zero. In MXFEM, the sign of the distance for the Ψ level set function is
positive on the side counter-clockwise from the direction of the crack tip speed function and
negative on the clockwise side. The sign of the distance function for the Φ function is positive
on the side in the direction of crack growth and negative on the opposite side. The crack is
defined to be the locations where the following conditions are true

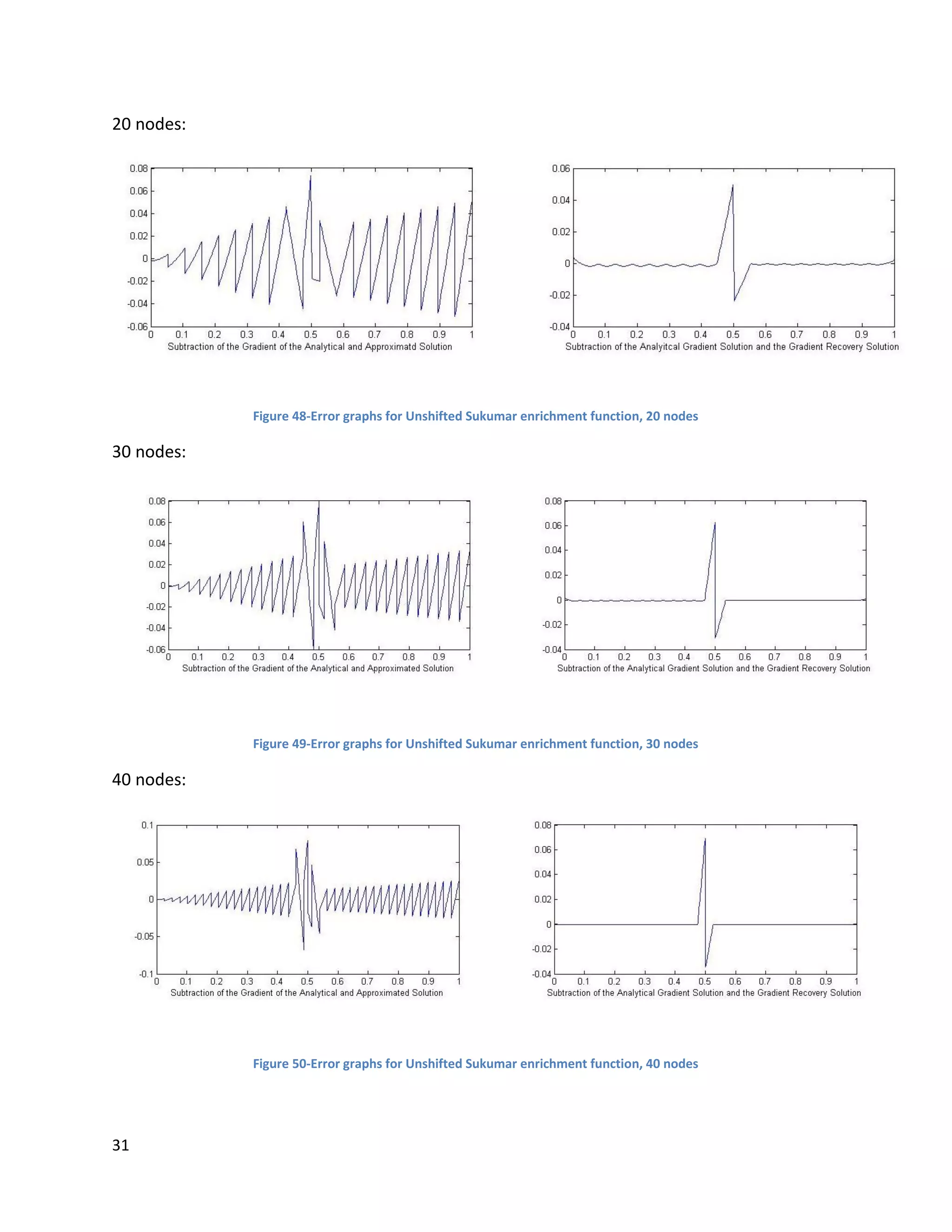
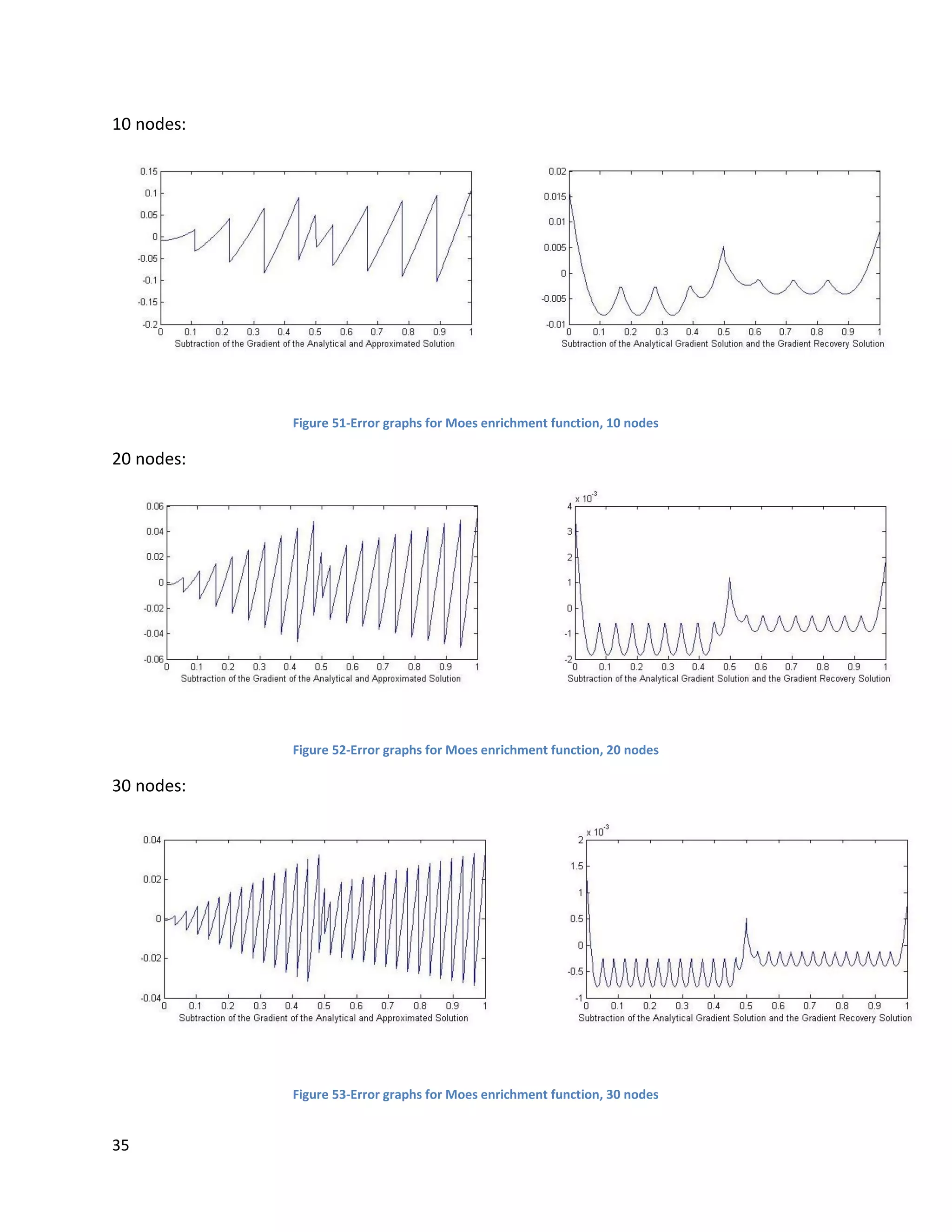
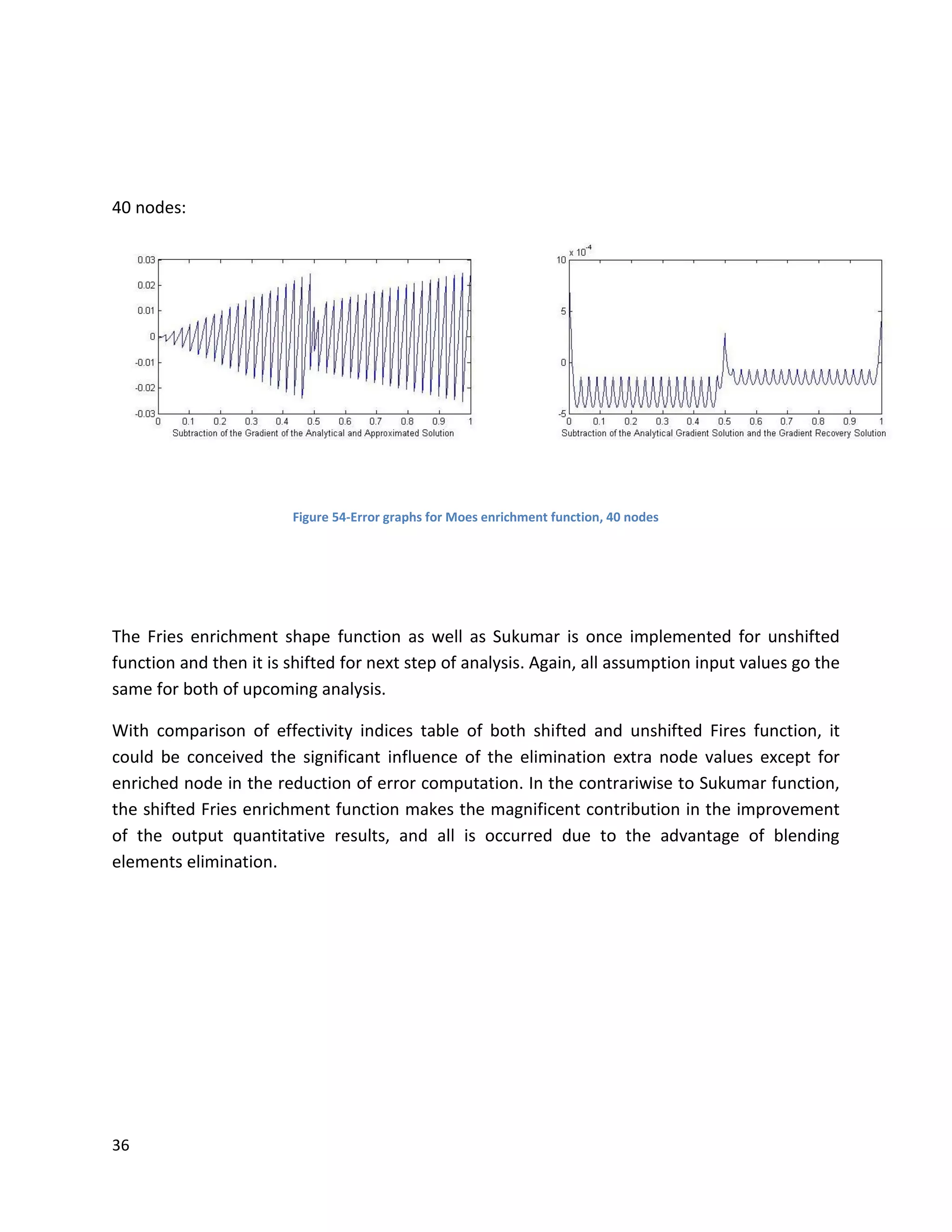
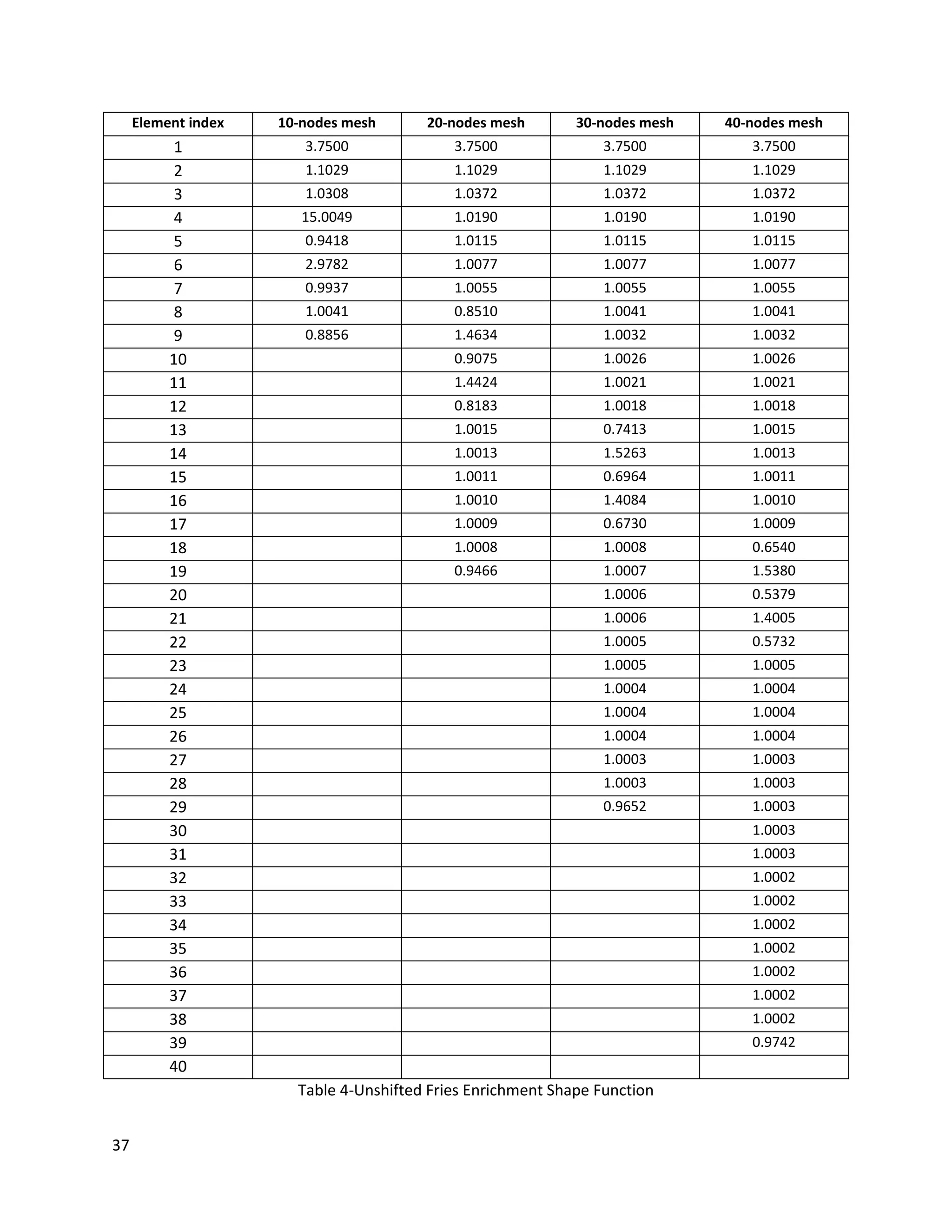
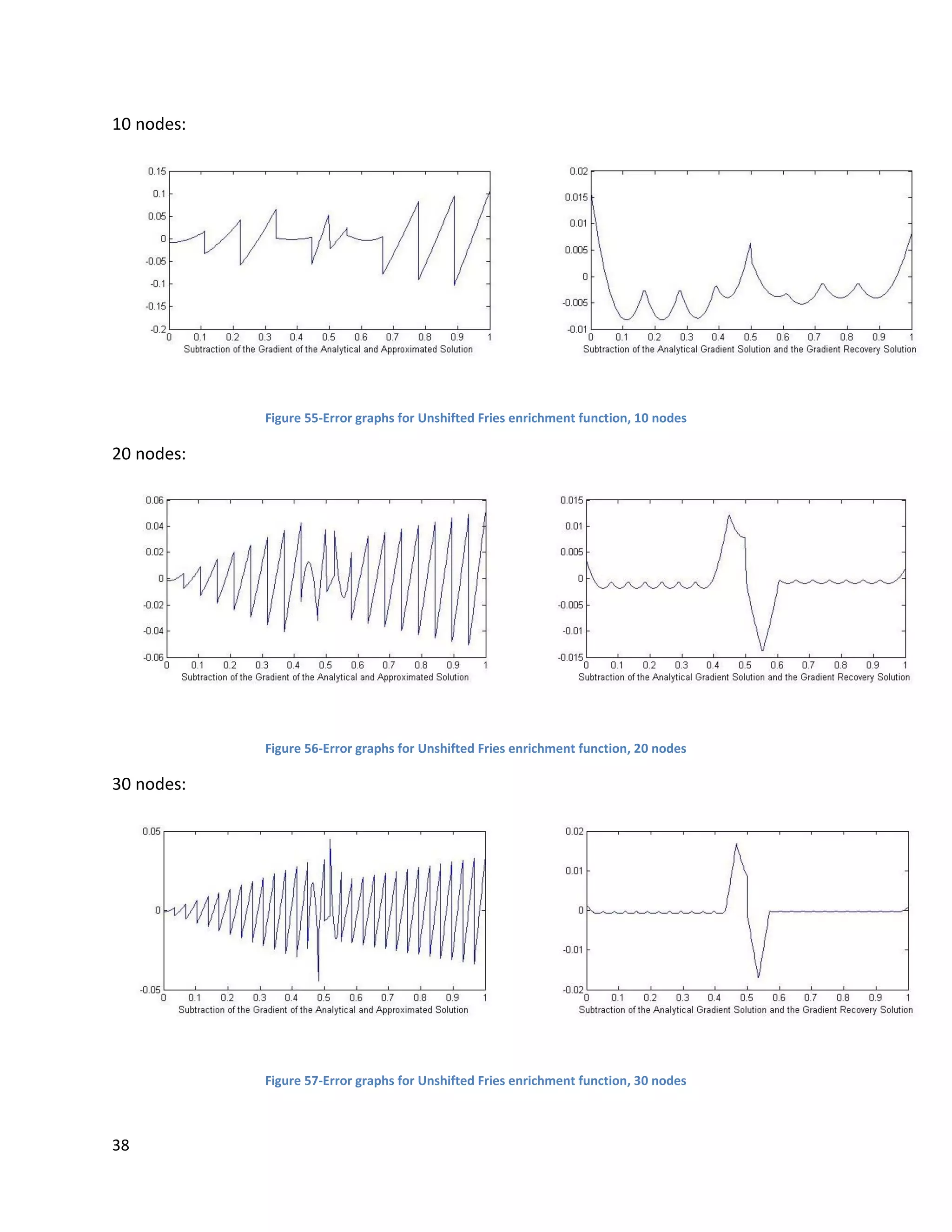
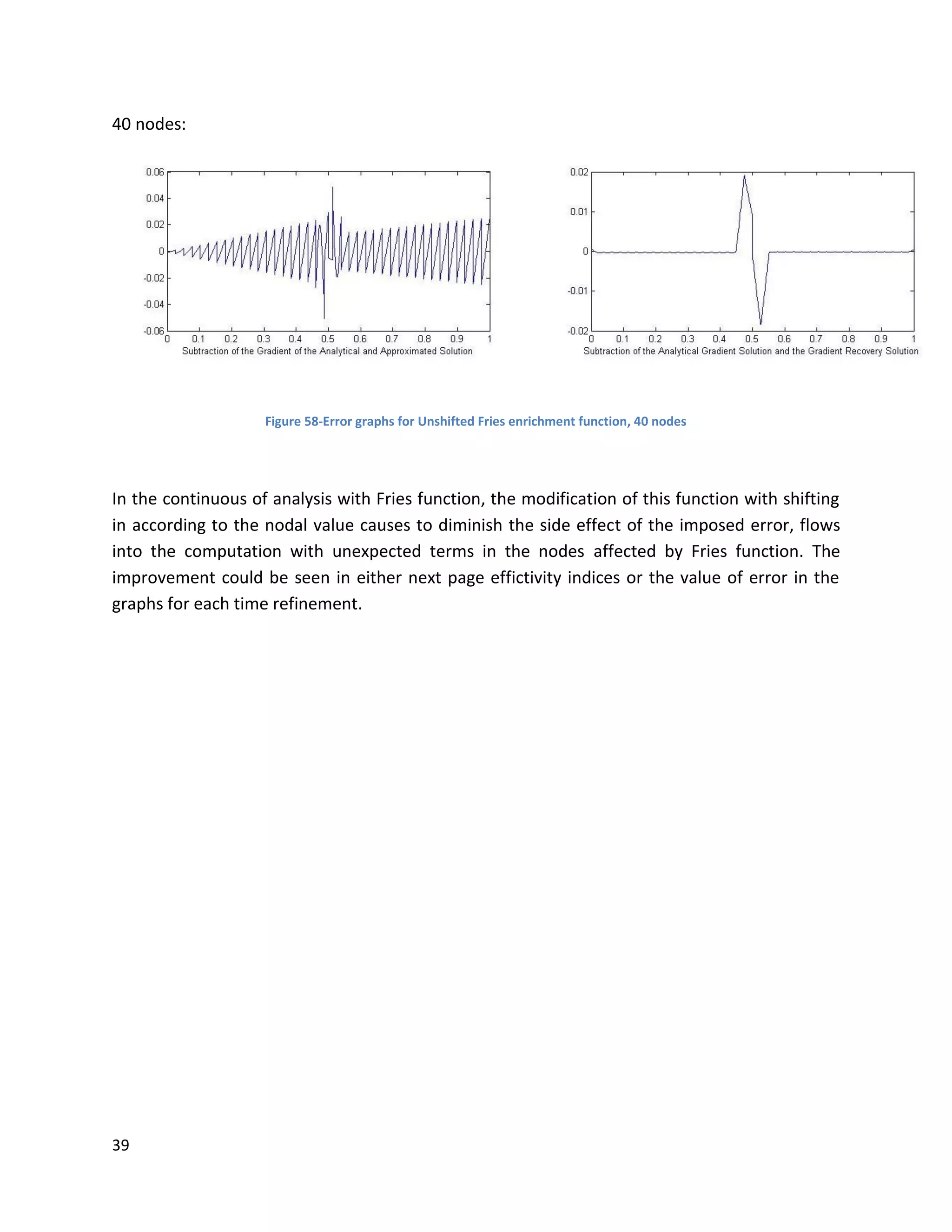
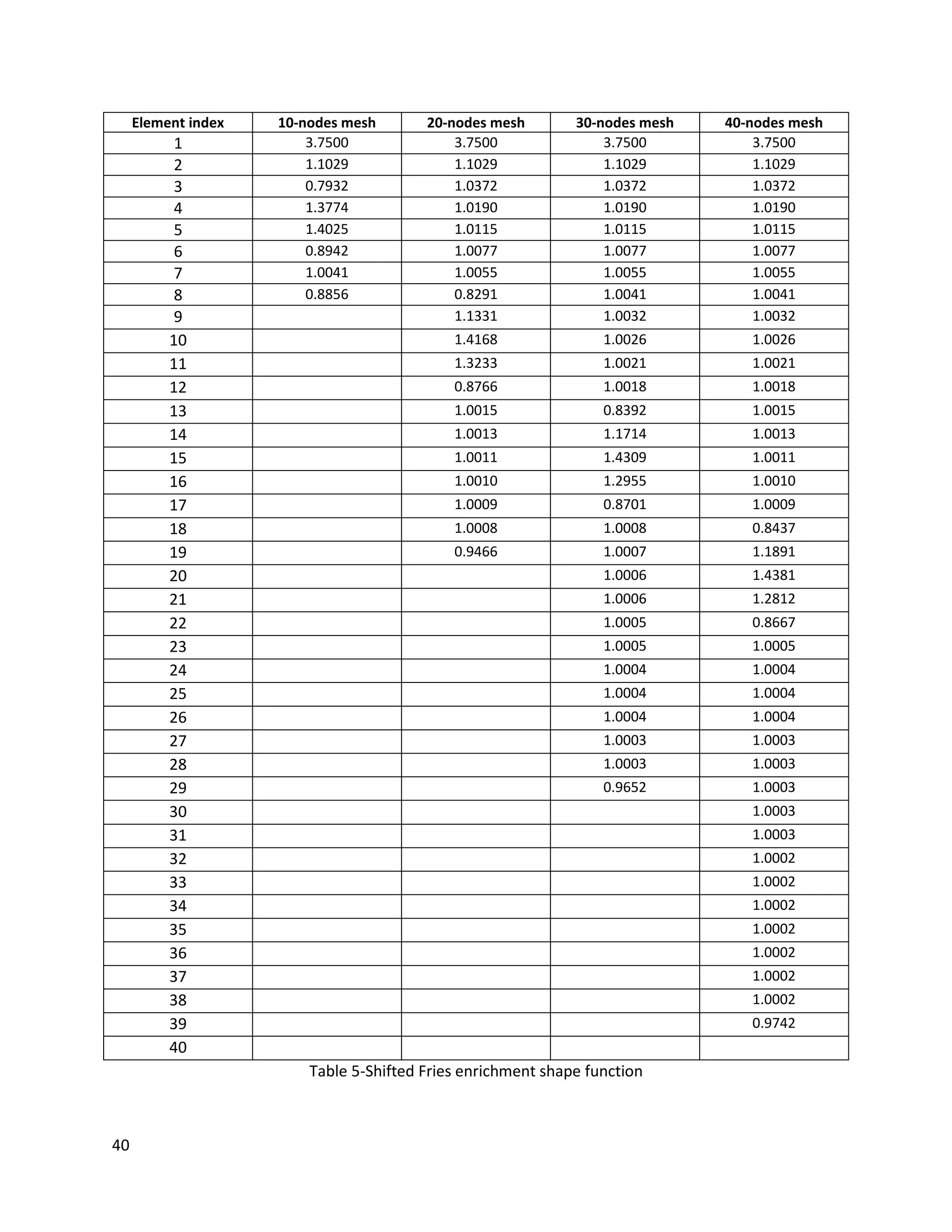
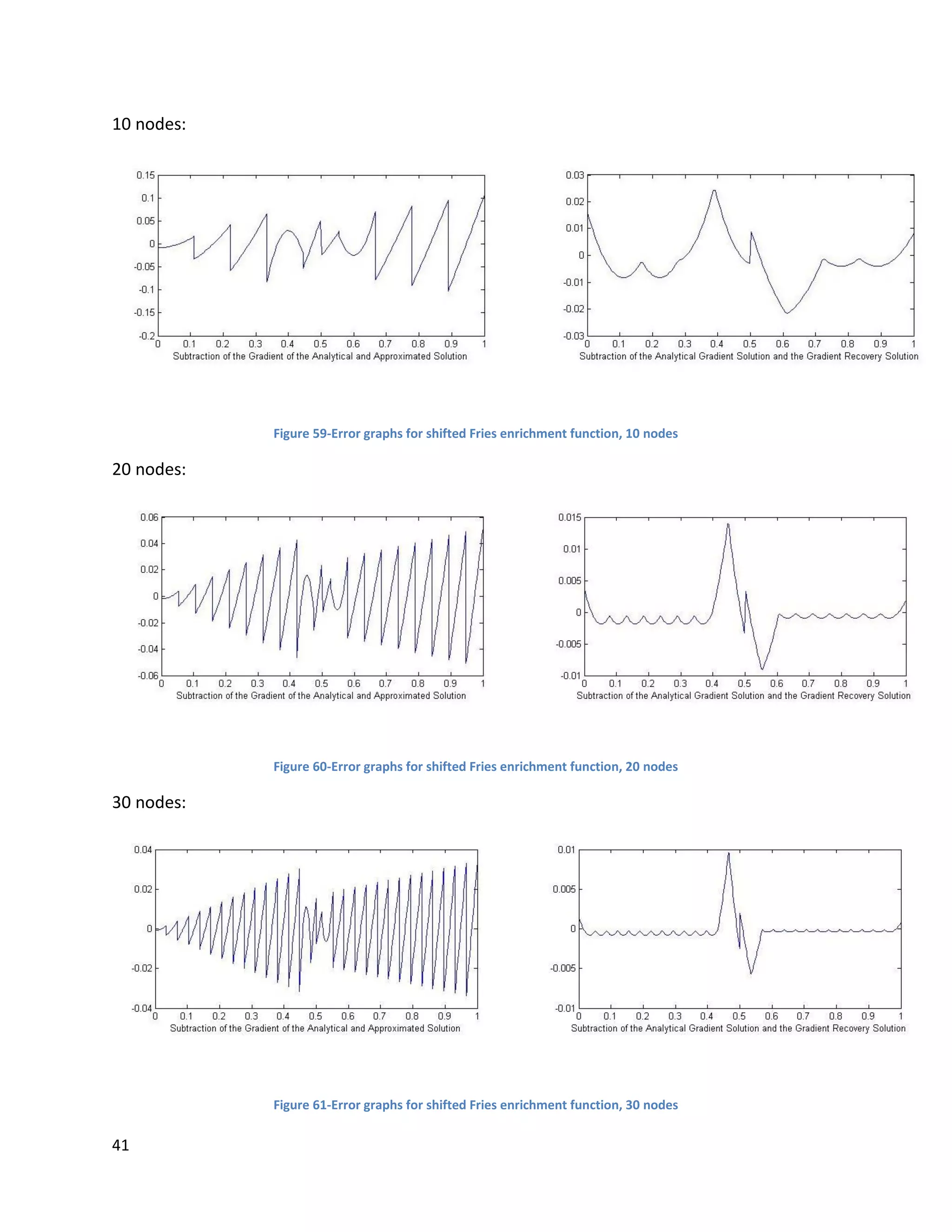
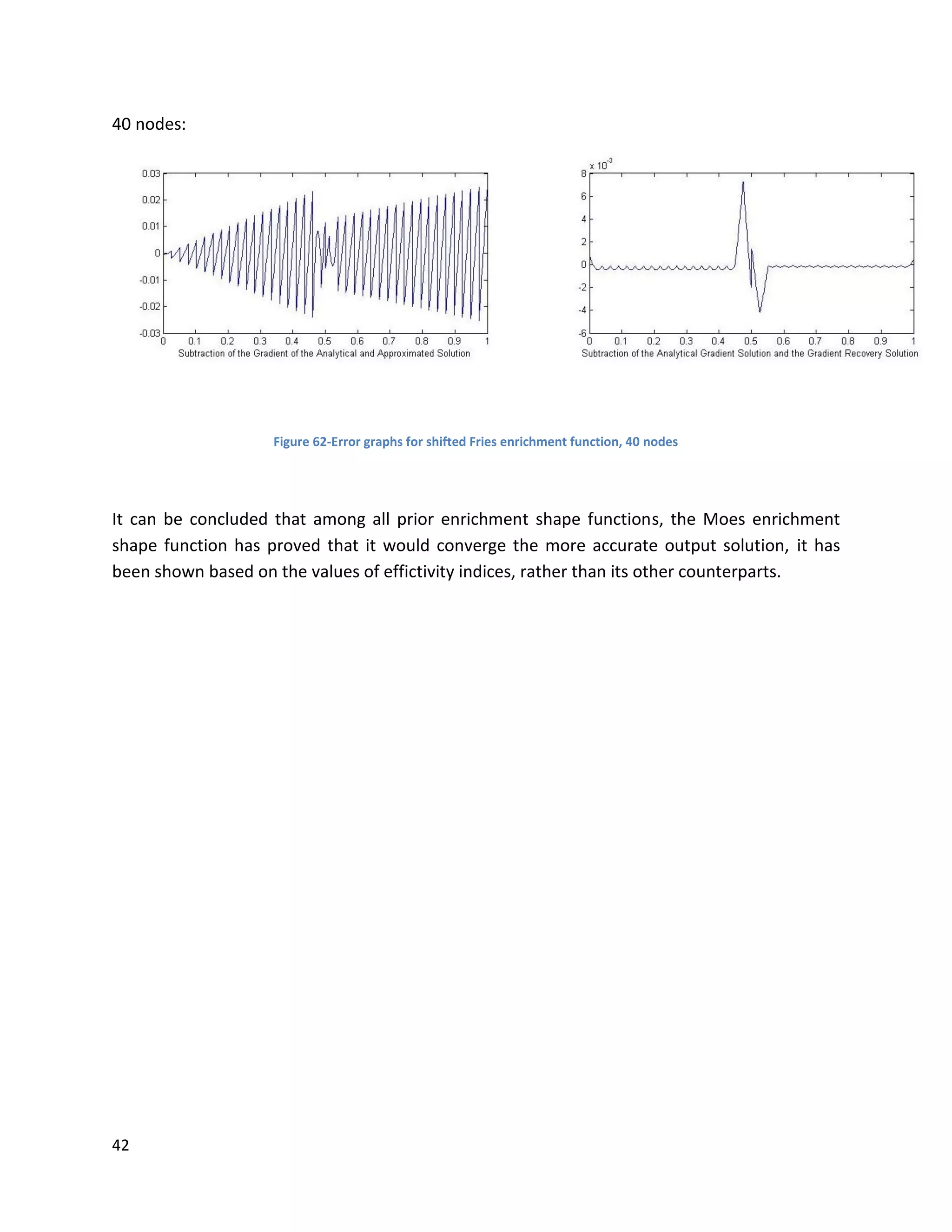
46
𝛷 𝑥 𝑡 , 𝑡 ≤ 0 (3.15)
𝛹 𝑥 𝑡 , 𝑡 = 0 (3.16)
The defined level set function goes for closed domain like as fig….
Figure 64-Example of a signed distance function for a closed domain [15].

47
Figure 65-Example of a signed distance function for an open section [15].
The general implementation form of XFEM is similar to what has been described in 1-D;
nonetheless, it is expanded to one dimension higher. Here again by exploiting the partition of
unity finite element method (PUFEM), the discontinuities are simulated independent of finite
element mesh. The XFEM gives the viability to catch a non-smooth behavior of field variables,
such as stress across the interface of dissimilar materials or displacement across cracks, with
adding the enrichment functions to the displacement approximation as long as the partition of
unity is satisfied. Some additional degrees of freedom are introduced in all elements where
discontinuity is present, and due to type of enrichment functions, possibly some neighboring
elements which are known as blending elements.
In the XFEM the approximation takes the form
𝑢 𝑕
= 𝑁𝐼(𝑥)
𝐼
[𝑢𝐼 + 𝑣 𝐽
(𝑥)
𝐽
𝑎𝐼
𝐽
] (3.17)
where 𝑢𝐼 are the classical finite element degrees of freedom (DOF), 𝑣 𝐽
𝑥 is the Jth
enrichment function at the Ith node, and 𝑎𝐼
𝐽
are the enriched DOF corresponding the Jth
enrichment function at the Ith node. On owing to introduction of enrichment functions into
approximation solution, the additional calculations are required to calculate the physical
variable, and hence the interpolation property does not satisfy in straight step, 𝑢𝐼 = 𝑢 𝑕
(𝑥𝐼).

48
The interpolation property is important in practice in applying boundary or contact conditions.
Therefore, it is common practice to shift the enrichment function such that
𝛾𝐼
𝐽
𝑥 = 𝑣 𝐽
− 𝑣𝐼
𝐽
(𝑥) (3.18)
where 𝑣𝐼
𝐽
𝑥 is the value of the Jth enrichment function at the Ith node. The shifted enrichment
function is able to satisfy 𝑢𝐼 = 𝑢 𝑕
(𝑥𝐼) and assign a value of zero to all standard FEM nodes. The
shifted displacement approximation is given by
𝑢 𝑕
= 𝑁𝐼(𝑥)
𝐼
[𝑢𝐼 + 𝛾𝐼
𝐽
(𝑥)
𝐽
𝑎𝐼
𝐽
] (3.19)
The Hook’s equation in linear elastic problem indicates the formulation as
𝒌𝒒 = 𝒇 (3.20)
where K is global stiffness matrix, q are nodal degree of freedom, and f are external forces. The
global stiffness matrix can be rearranged in order to
K=
𝒌 𝑢𝑢 𝒌 𝑢𝑎
𝒌 𝑎𝑢
𝑇
𝒌 𝑎𝑎
where 𝒌 𝑢𝑢 is the classical finite element stiffness matrix, 𝒌 𝑎𝑎 is enriched finite element stiffness
matrix, and 𝒌 𝑢𝑎 is a combination of the classical and enriched stiffness matrix components.
Each component of global stiffness matrix K is computed by the integration such as
𝑲 𝑒 = 𝑩 𝛼
𝑇
𝑪𝑩 𝛽 𝑑𝛺 𝛼, 𝛽 = 𝑢, 𝑎 (3.21)
where C is the constitutive matrix for an isotropic linear elastic material, 𝑩 𝑢 is the classical
strain-displacement matrix, and 𝑩 𝑎is the enriched strain-displacement matrix. Both strain-
displacement matrices are illustrated like
𝑩 𝑢 =
𝑁𝐼,𝑥 0 0
0 𝑁𝐼,𝑦 0
0 0 𝑁𝐼,𝑧
0 𝑁𝐼,𝑧 𝑁𝐼,𝑦
𝑁𝐼,𝑧 0 𝑁𝐼,𝑥
𝑁𝐼,𝑦 𝑁𝐼,𝑥 0
; 𝑩 𝑎 =
(𝑁𝐼 𝛾𝐼
𝐽
),𝑥 0 0
0 (𝑁𝐼 𝛾𝐼
𝐽
),𝑦 0
0 0 (𝑁𝐼 𝛾𝐼
𝐽
),𝑧
0 (𝑁𝐼 𝛾𝐼
𝐽
),𝑧 (𝑁𝐼 𝛾𝐼
𝐽
),𝑦
(𝑁𝐼 𝛾𝐼
𝐽
),𝑧 0 (𝑁𝐼 𝛾𝐼
𝐽
),𝑥
(𝑁𝐼 𝛾𝐼
𝐽
),𝑦 (𝑁𝐼 𝛾𝐼
𝐽
),𝑥 0

49
where each matrix constitutes from derivative of either standard or enriched shape function
with respect to each corresponding axis.
It is going to be apparent that the shape function matrix contains the same number of columns
as in the strain-displacement matrix, whose components for the 4-node planar element is used
as in fig…
Figure 66-Physical and parent 4-node elements [5].
The shape functions 𝑁𝐼 (I from 1 to 4) are bi-linear in r and s (coordinates in the parent
element):
𝑁1 =
1
4
(1 − 𝑟)(1 − 𝑠) (3.22)
𝑁2 =
1
4
(1 + 𝑟)(1 − 𝑠) (3.23)
𝑁3 =
1
4
(1 + 𝑟)(1 + 𝑠) (3.24)
𝑁4 =
1
4
(1 − 𝑟)(1 + 𝑠) (3.25)

50
The interpolation of the displacement or nodal DOF from parent element to physical element
with aid of shape functions are carried on as
𝑢 𝑒
𝑀 = 𝑁 𝑒
𝑀 𝑞 𝑒 (3.26)
As if
𝑁 𝑒
𝑀 = [𝑁𝑠𝑡𝑑
𝑒
𝑀 𝑁𝑒𝑛𝑟
𝑒
𝑀 ]
The q and f matrices are both identically given by
𝒒 𝑇
= {𝒖 𝒂} 𝑇
where u and a are vectors of the classical and enriched degrees of freedom and
𝒇 𝑇
= {𝒇 𝑢
𝑇
𝒇 𝑎
𝑇
}
where 𝒇 𝑢 and 𝒇 𝑎 are vectors of the applied forces for the classical and enriched components of
the global force matrix. The vectors 𝒇 𝑢 and 𝒇 𝑎 are given by calculation of tractions t and body
forces b over whole domain in the way as
𝒇 𝑢 = 𝑁𝐼 𝑡 𝑑Ƭ + 𝑁𝐼 𝑏 𝑑𝛺 (3.27)
and
𝒇 𝑎 = 𝑁𝐼 𝑡 𝛾𝐼
𝐽
𝑑Ƭ + 𝑁𝐼 𝑏 𝛾𝐼
𝐽
𝑑𝛺 (3.28)
The stress and strain should be calculated in the sense of consideration for realizing the
discontinuity. Therefore, the strain and stress may be computed as
𝜀 = 𝑩 𝑢 𝑩 𝑎 {𝑢 𝑎} 𝑇 (3.29)
and
𝜎 = 𝐶𝜀 (Constitutive Equation) (3.30)
3.2.1 Crack Enrichment Function
In general, XFEM is used to describe the discontinuity as either weak or strong. A strong
discontinuity can be considered one where both the displacement and strain are discontinuous,

51
while a weak discontinuity has a continuous displacement but a discontinuous strain. The crack
discontinuity is categorized in the strong discontinuity. The modeling of cracks in the XFEM has
been thoroughly investigated. Belytschko was the first to bring the study of cracks into XFEM,
and Moes simplify the enrichment function along the crack by introduction of the Heaviside
function away from crack tip. The common practice is to incorporate two enrichment functions
into XFEM displacement approximation to represent a crack. The Heaviside step function for
enrichment of crack away from its tip is given as
h(x)=
+1 𝑎𝑏𝑜𝑣𝑒 𝑐𝑟𝑎𝑐𝑘
−1 𝑏𝑒𝑙𝑜𝑤 𝑐𝑟𝑎𝑐𝑘
In the particular instance of 2D crack Modeling, the enriched displacement approximation is
written as
𝑢 𝑕
𝑥 = 𝑁𝐼 𝑥 𝑢𝐼
𝐼∈𝑁
+ 𝑁𝐽 𝑥
𝐽∈𝑁 𝑑𝑖𝑠𝑐
𝐻𝐽 𝑥 𝑎𝐽 + 𝑁 𝐾 𝑥 𝐵 𝛼𝐾 𝑥 𝑏 𝛼𝐾
4
𝛼=1𝐾∈𝑁 𝑎 𝑠𝑦𝑚𝑝𝑡
(3.31)
where N is the set of conventional (not enriched) nodes, 𝑁 𝑑𝑖𝑠𝑐
is the set of nodes whose
support is entirely split by the crack, 𝑁 𝑎𝑠𝑦𝑚𝑝𝑡
is set of nodes which contain the crack tip in the
support of their shape functions. 𝐻𝐽 is a modified Heaviside step function actives on node J and
defined by
𝐻𝐽 𝑥 = 𝐻 𝑥 − 𝐻(𝑥𝐽 ) (3.32)
The functions B are assigned to crack tip nodes in the asymptotic fields. The 𝑢𝐼’s are the
unknown standard displacement degrees of freedom associated with node I, the 𝑎𝐽 ’s are the
unknown enrichment coefficients associated with nodes in correspondence with element
crossed by crack. Finally, 𝑏 𝛼𝐾 ’s are additional enrichment degrees of freedom associated with
modified enrichment function 𝐵 𝛼𝐾 active on node K and defined by
𝐵 𝛼𝐾 𝑥 = 𝐵𝛼 𝑥 − 𝐵𝛼(𝑥 𝐾) (3.33)

52
Figure 67-Selection of enriched nodes for 2D crack problem. Circled nodes are enriched by the step function whereas the
squared nodes are enriched by the crack tip functions. (a) on a structured mesh; (b) on an unstructured mesh [5].
The B-branch functions as crack tip enrichment functions in isotropic elasticity are provided
from the asymptotic displacement fields.
𝑩 ≡ 𝐵1, 𝐵2, 𝐵3, 𝐵4 = [ 𝑟 sin
𝜃
2
, 𝑟 cos
𝜃
2
, 𝑟 sin
𝜃
2
cos 𝜃 , 𝑟 cos
𝜃
2
cos 𝜃]
Here, r and 𝜃 are polar coordinates in the local crack tip coordinate system as shown in fig…
The first element of branch function represents the discontinuity near the tip, while the other
three functions help to get accurate result with relatively coarse meshes. It has not been
proved yet by adding higher order terms in the asymptotic expansion of the near-tip fields
substantially enhance the improvement of solution.

53
Figure 68-Coordinate configuration for crack tip enrichment function [5].
Because the XFEM mesh does not need to conform to the domain, a method must be used to
track of the location of the cracks. Those mentioned level set functions are going to shed the
light to find the crack path. The zero level set of 𝛹(𝑥) represents the crack body, while the zero
level sets of 𝜑(𝑥), which is orthogonal to the zero level set of 𝛹(𝑥), represents the location of
the crack tips. The enrichment functions in terms of 𝜑(𝑥) and 𝛹(𝑥) can be noticed such as
𝑕 𝑥 = 𝑕 𝛹 𝑥 =
+1 𝑓𝑜𝑟 𝛹(𝑥) > 0
−1 𝑓𝑜𝑟 𝛹(𝑥) < 0
(3.34)
Furthermore, the polar crack tip coordinates are given as
𝑟 = 𝛹2 𝑥 + 𝛷2(𝑥) and 𝜃 = tan−1 𝛹(𝑥)
𝛷(𝑥)
The enrichment of nodes according to crack tip enrichment can also be determined through the
use of level set functions defining the crack. Consider an element where the maximum and
minimum values of 𝛹(𝑥) and 𝜑(𝑥) are given as 𝛹𝑚𝑎𝑥 , 𝛹 𝑚𝑖𝑛 , 𝛷 𝑚𝑎𝑥 , and 𝛷 𝑚𝑖𝑛 . Then an element
is enriched with the Heaviside enrichment when
𝛷 𝑚𝑎𝑥 <0 and 𝛹𝑚𝑎𝑥 𝛹 𝑚𝑖𝑛 ≤ 0

54
And the crack tip enrichment when
𝛷 𝑚𝑎𝑥 𝛷 𝑚𝑖𝑛 ≤ 0 and 𝛹𝑚𝑎𝑥 𝛹 𝑚𝑖𝑛 ≤ 0
Hence, the compilation of extended finite element method and level set method turns out to
be the best application for tracking crack.
3.2.2 Inclusion Enrichment Function
The enrichment function for simulation and implementation of material interfaces independent
of the finite element mesh though the partition of unity as well as element-free Galerkin should
be able to incorporate the behavior of weak discontinuity. The enrichment function for
interface problem should possess the capability of satisfying the Hadamard condition as
𝐹+
− 𝐹−
= 𝒂 ∗ 𝑛+ (3.35)
where F is the deformation gradient, 𝑛+
is the outward normal material interface, and 𝒂 is an
arbitrary vector in the plane.
Sukumar first introduced the use of the absolute value function likewise the level set function
ξ(x) for enrichment, which gives the shortest signed distance from a given point to the interface
between the two materials. Therefore, the enrichment function takes the form:
𝑣 𝑥 = |𝜉 𝑥 | (3.36)
The enrichment function is assumed to be nonzero only over the domain of support for the
enriched nodes, as with the crack enrichment function. The Sukumar enrichment function for
implementation at the bi-material boundary value benchmark problem causes to lead to a
convergence rate which was lower than the equivalent traditional finite element method
problem where the mesh conforms with the material interface. The main reason for
deterioration of convergence rate roots in the blending element with partial enrichment nodes.
Hence, the Moes proposed the enrichment function, which is able to eliminate the
repercussion of blending elements, takes the form of
𝛾 𝑥 = 𝑁𝐼 𝑥 𝜉𝐼 − 𝑁𝐼(𝑥)𝜉𝐼
𝐼𝐼
(3.37)
One characteristic of this shape functions is going to be in the way it is zero at all nodes and
thus, does not need to be shifted such that all standard degrees of freedom are recovered
automatically. If an interface corresponds to the mesh, then no nodes are enriched as the
enrichment function will be zero and the problem will be equivalent to the standard finite

55
element problem. Currently, this enrichment function is considered for simulation of inclusion
with XFEM at the 2-D code. Besides, in the current some modification is taken up in accordance
to the enrichment shape function to enhance more accurate convergence rate. The
modification is come with an element-based enrichment instead of nodal enrichment where
the displacement approximation took the form
𝑢 𝑕
𝑥 = 𝑁𝐼 𝑥 𝑢𝐼 + 𝑣(𝑥)𝑎 𝑒
𝐼
(3.38)
where 𝑣 𝑥 is a piecewise linear enrichment function where
𝑣 𝑥 =
𝑣𝐼 𝑥 = 0
𝑣 𝜉 𝑥 = 0 = 1
(3.39)
And 𝑎 𝑒 are elemental degrees of freedom. The enrichment function gives the value of zero at
all nodes and takes a value one at the interface. The proposed method permits the availability
for equality between the number of elemental degrees of freedom and the number of
dimensions of the problem. Therefore, the resulting system of equations needs fewer degrees
of freedom than either the standard and extended finite element method to represent the
same domain. All enrichment function types eventually yield equivalent final answers.
However, by adding elements or refinement of mesh, the smoothing of the absolute value
enrichment encounter to a challenge for recovering the theoretical displacement, but this is not
with Moes enrichment function or element-based enrichment. Commonly, the Moes
enrichment shape function is the most applicable function for modeling of inclusion with XFEM
due to its improved convergence rate.
3.2.3 Void Enrichment Function
The void was firstly represented with XFEM by Daux. Later on, Sukumar extended the void
enrichment function with the specification characteristic of 𝜒(𝑥) level set function to track the
void. One of the advantages of void enrichment function is that it does not require additional
DOF, instead the displacement approximation for a domain with a hole takes the form
𝒖 𝑕
𝑥 = 𝑉(𝑥) 𝑁𝐼(𝑥)𝑢𝐼
𝐼
(3.40)
where 𝑉(𝑥) takes a value of 0 inside the void and 1 anywhere else. In practice, integration is
not carried out where 𝜒(𝑥) < 0. Additionally, nodes whose support is completely within the
void are considered the fixed DOF.

56
3.2.4 Element integration with discontinuity
In the derivation of weak form in the XFEM, the numerical integration should be performed on
the divergence theorem to lower continuity requirements on the trial function. Standard Gauss
quadrature requires that the integrals are smooth, which is not the case for an element
containing a strong or weak discontinuity. The integration challenges for crossed element with
discontinuity was resolved by Moes proposition that was to divide a two dimensional element
into a set of triangular subdomains, where the discontinuity must be an internal boundary of
the domain of integration. Integration would then be performed over each subdomain instead
of performing the integration over polygonal domains, see fig…. The two types of partitioning
an element and the associated sub-triangles are shown as if one element cut entirely by crack,
another one contains the crack tip. The common number of gauss points for integration in each
triangular subdomain with the Heaviside enrichment is 3 and the crack tip enrichment function
considers 7 of them.
The numerical integration procedure for elements contain the discontinuity is as follows
1. Build the Delauney triangulation to get the sub-triangles.
2. For each sub-triangle, the coordinates and weights of 13 Gauss points are computed
and then converted into the parent coordinate system of the original element.

57
Figure 69-Sub-triangulation of finite elements [6].
The MATLAB code was implemented for two-dimensional plane stress and plane strain
problems. The code is mainly developed for rectangular domain as structured grid of linear
square quadrilateral elements with arbitrary loading and boundary conditions. The enrichments
would be covered the homogenous crack, inclusion and void. All discontinuities are tracked
using level set method as well as calculation of enrichment functions. The 𝛷(𝑥) and 𝛹(𝑥) level
set functions track the crack, the χ(x) level set functions determine the boundary of void, and
the 𝜉(𝑥) level set function traces the inclusion. Integration of enriched elements is conducted
through the subdivision of elements into triangle regions.

58
3.3. Error Estimation in Bilinear Finite Element Approximation
The coming description of error estimation is considered in two dimensional finite element
approximation. The rectangular domain is refined to the square elements with length sides of h
for each time discretization to compute the possessed error. The analogy of error estimation is
defined in the post-processing procedure by sampling the gradients of the finite element
approximation at the centroids of the elements. These values are then averaged to produce an
approximation to the gradient at the nodes as shown in fig…. Here again, the recovered
gradient 𝐺𝑥(𝑢 𝑥) is selected as if being able to interpolate the values recovered at the nodes
with the bilinear function in each component. The local estimator ƞ 𝑘 on element K is
ƞ 𝑘 = 𝐺𝑥 𝑢 𝑥 − ∇𝑢 𝑥 𝐿2 𝑘 (3.41)
As it was also mentioned in one dimensional error analysis, the reason behind sampling at the
centroids is found on the superconvergence property stands as follow:
𝑢 𝑥 − 𝐼𝑥 𝑢 𝐻1 𝛺 ≤ 𝐶𝑕2
𝑢 𝐻3 𝛺 (3.42)
where 𝐼𝑥 is the bilinear interpolant at the vertices of the partition.
The operator 𝐺𝑥 should satisfy several conditions and all aim is toward to be found
𝐺𝑥 𝐼𝑥 𝑣 ≡ 𝐼𝑥(∇𝑣) (3.43)
whenever 𝑣 ∈ 𝑃2(quadratic polynomial). If the interpolation is considered for single element,
the value of 𝐼𝑥∇𝑣 at the centroid is the average of the values of the gradients at the element
vertices
∇ 𝐼𝑥 𝑣 =
𝑕
0
→ 𝐼𝑥∇𝑣 =
𝑕
0
(3.44)
It can be perceived the sampled values coincide at the centroids. Sequentially, the values at the
vertices will also coincide since the bilinear interpolation is applied the simple averaging that is
consistent.
Another estimator could be compared with recovery estimator is Kelly estimator. Using the
midpoint rule for integration along each side of the element, the estimator would end up to
ƞ2
=
𝑕2
24
𝜕𝑢 𝑥
𝜕𝑚
2
𝛾⊂𝜕𝐾
(3.45)

59
where the discontinuities are evaluated at the midpoint of the sides. The gradient recovery-
based estimator might seem to be too complicated to be of practical use. However, the Kelly
estimator may be viewed as a modified recovery operator by taking the values of the recovered
gradient at the vertices likewise fig…
Figure 70-Construction of recovered gradient at vertex of element K. The value at • is a linear combination of the values at o
using the weights indicated [9].

60
As matter of the fact, these set of conditions should suffice for the operators 𝐺𝑥 guaranteeing
that 𝐺𝑥(𝐼𝑥 𝑢) is a good approximation to the true gradient ∇𝑢. This type of condition is generally
referred to as consistency in the context of numerical algorithm. The consistency condition
holds the reality of that is when the finite element approximation is exact, then the true error
and the estimate resulting from the recovery-based procedure will turn to be zero. This
condition can be formulated as if u is a polynomial of degree p+1 on the patch 𝐾 associated
with an element K- that is, 𝑢 ∈ 𝑃𝑝+1(𝐾 ), then
𝐺𝑥 𝐼𝑥 𝑢 = 𝐼𝑥∇𝑢 𝑜𝑛 𝐾, (3.46)
where 𝐼𝑥 is the X-interpolant. The polynomial space 𝑃𝑝+1 is validated for both triangular and
quadrilateral elements. However, the consistency condition does not determine the recovery
operator 𝐺𝑥 exactly.
Another property of gradient recovery runs around its computation cost. Ideally, it should be
possible to compute the recovered gradient 𝐺𝑥 without recourse to global computation;
otherwise, it would be simpler to resolve the original finite element problem on a finer
partition. The most suitable approaches are those whereby the recovered gradient at a point 𝑥0
is a linear combination of values of the gradients of the finite element approximation sampled
in patch 𝐾 belongs to element K contains the point 𝑥0.
The condition is configured over the patches 𝐾 primarily for convenience. In principle, there is
no reason why a larger patch should not be employed if desired. However, the recovery
procedures outlines that the patch 𝐾 provides sufficiently flexible framework to incorporate
most practical schemes.
The gradient recovery should be regulated in the way that may be able to handle efficiently by
the existing data structures within the finite element code. It would be simple enough to be
evaluated and integrated easily. The boundedness and linearity condition of 𝐺𝑥 leads to the
following statement:
If 𝐺𝑥 : X → X*X is a linear operator, and there exists a constant C (independent of h) such that:
𝐺𝑥 𝑣 𝐿∞ 𝐾
≤ 𝐶 𝑣 𝑊3,∞ 𝐾 (3.47)
where X id finite element subspace.
With satisfaction all above conditions through the computation of gradient recovery operator
𝐺𝑥, its standard approximation formulation is found that

61
∇𝑢 − 𝐺𝑥 𝐼𝑥 𝑢 𝐿2 𝛺
≤ 𝐶𝑕 𝑝+1
𝑢 𝐻 𝑝+2 𝛺 (3.48)
The P is a regular partitioning of the domain Ω into triangular and quadrilateral elements and
let X be the finite element subspace based on polynomial degree p. Also, C>0 is independent of
field variable u and h as the largest size of element in the refined domain. The outcome of the
above equation gets lot closer to good approximation with applying 𝐺𝑥 to the finite
approximation with assumption of superconvergence points. When 𝐺𝑥 satisfies all the
corresponding conditions, the superconvergence holds
∇𝑢 − 𝐺𝑥 𝑢 𝑥 𝐿2 𝛺 ≤ 𝐶 𝑢 𝑕 𝑝+𝜏
(3.49)
where C>0 is independent of h, and in fact with the biggest value of h makes the inequality
more optimal. The 𝑢 ∈ 𝐻 𝑝+2
(𝛺) and 𝜏 is positive. It finally should tend to realize the equality in
values between recovery-based estimator and true error as
lim
𝑕→0
ƞ
| 𝑒 |
= 1 (3.50)
For current project, the implementation of a posteriori error estimation is developed by the so-
called superconvergent patch recovery (SPR) procedure proposed by Zienkiewicz and Zhu. The
basic method is applicable to the mesh refined with triangular and quadrilateral elements.
Every node 𝑥 𝑘, 𝐾 ∈ 𝑁, is an element vertex, and consequently, the patch 𝛺 𝑘 consists of the
elements having 𝑥 𝑘 as a vertex. The gradient is assigned to the centroid 𝑐 𝑘 of 𝐾 in the patch 𝛺 𝑘.
The values of the gradients sampled at the centroids in the patch are used to generate a
recovered value at the central node by first fitting each component of the gradient data to a
function of the form
𝑝(𝑥) 𝑇
𝛼 (3.51)
where the vector p is founded on the polynomial degree of basic shape function used to
construct the finite element space X, and it might linear or quadratic finite element
approximation on triangular element.
𝑝 𝑥 =
1
𝑥
𝑦
𝑜𝑟
1
𝑥
𝑦
𝑥2
𝑥𝑦
𝑦2
(3.52)

62
for linear and quadratic polynomial function, respectively. 𝛼 is a vector of coefficients to be
determined. The coefficients are wound up with a help of the discrete least square fit based on
the values at the sampling points. The Euler condition for the minimizer divulges that 𝛼 is the
solution of the matrix equation
𝑀𝛼 = 𝑏 (3.53)
where M is the matrix
𝑀 = 𝑝(𝑐 𝑘)𝑝(𝑐 𝑘) 𝑇
𝐾⊂𝛺
(3.54)
and b is the vector
𝑀 = 𝑝 𝑐 𝑘
𝑇
𝜕𝑢 𝑥
𝜕𝑥
(𝑐 𝑘)
𝐾⊂𝛺
(3.55)
At the end, the recovered (x-component) of the gradient flux at the central node is defined to
be
𝑔 𝑘 𝑢 𝑥 = 𝑝(𝑥 𝑘) 𝑇
𝛼 (3.56)
for linear polynomial. In terms of quadratic polynomial function the vertices 𝑥𝑙and 𝑥 𝑟 are
defined where the mid-side point is located. Thus, if coefficient 𝛼𝑙 and 𝛼 𝑟 are obtained when
fitting the data at the averaged nodes, then the recovered value at the mid-side node is taken
to be a simple arithmetic average of the values
𝑔 𝑘 𝑣 =
1
2
𝑝(𝑥 𝑘) 𝑇
𝛼𝑙 +
1
2
𝑝(𝑥 𝑘) 𝑇
𝛼 𝑟 (3.57)
The patch recovery technique for quadrilateral element follows more or less the same
approach that was defined for triangular elements; nonetheless, with some modification. The
gradient is sampled at Gauss quadrature points. The functions used in vector p(x) are
constructed in the space that was used for the finite element subspace X. There would be the
case of if the nodes are located on the interior of an element. The approach implied is a simple
averaging of the values gained in the fitting the gradient over each of four patches associated
with the corresponding node of the element.
The main scheme of SPR implementation for this project is owed to proposed method of
Cartensen particularly for enriched elements. With specifying the location of interface into the
corresponding elements that mount the effort of computation relatively higher with defining

63
two set of gradient points for above and below the interface location. The rest of procedures
are kept carrying on as the same was explained in this chapter.
3.4. Implementation and Results-2D
The analysis has been carried out in according to the three different available exact solutions.
At the beginning, it was presumed that there is no body force along the domain, then the body
force was allocated with the constant unit value in the vertical coordinate and zero all long at
horizontal coordinates, and for the last sequence of analysis the body force was substituted
with linear equation in y direction, and again zero for x direction. For each analysis the module
of elasticity matrix meets the requirement of plane strain hypothesis. Consequently, the plane
stress thickness is assigned to be zero as well as critical intensity stress factor for domain. The
geometry of domain is considered to be clamped at the vertical bottom side and stretched at
the top with magnitude force of ten. The dimension is taken to be unit for both sides. The
whole domain splits up into two different materials with assumption of zero Poisson ratio for
both of them. There are four times refinements in assessment and representation of results. It
started from division each length by 11 and ended up to 41.
The effictivity indices and correlated graphs is sorted in this sequence that the first analysis
belongs to the domain with zero body force, and then the constant and linear body force are
taken into the computation of a posteriori error estimation.

64
Zero Body Force
Node Numbers 𝑕 = 1
11 𝑕 = 1
21 𝑕 = 1
31 𝑕 = 1
41
1 0.0001 0 0 0
2 0.0003 0 0 0
3 0.0006 0.0001 0 0
4 0.0009 0.0001 0 0
5 0.0028 0.0002 0 0
6 0.0023 0.0001 0 0
7 0.0031 0.0005 0 0
8 0.0058 0.0003 0.0001 0
9 0.0087 0.0005 0.0001 0
10 0.0315 0.0006 0.0001 0
11 0.3693 0.0007 0.0002 0
12 0.0002 0.0003 0
13 0.0005 0.0004 0.0001
14 0.001 0.0004 0.0001
15 0.0021 0.0001 0.0001
16 0.0013 0.0007 0.0001
17 0.0034 0.0001 0.0002
18 0.0037 0.0002 0.0001
19 0.0142 0.0003 0.0001
20 0.0389 0.0004 0.0007
21 0.2153 0.0005 0.0003
22 0.0011 0.0003
23 0.0013 0.0001
24 0.0015 0.0001
25 0.0025 0.0002
26 0.0029 0.0002
27 0.0033 0.0004
28 0.0036 0.0004
29 0.0107 0.0003
30 0.0396 0.0004
31 0.2068 0.0006
32 0.0005
33 0.0008
34 0.0012
35 0.0015
36 0.0021
37 0.0028
38 0.0036
39 0.0109
40 0.0289
41 0.0609
Table 6-Effectivity indices for zero body force

65
Figure 71-The comparison of the exact and approximated solution for the zero body force
Figure 72-Stress y-y distribution for the zero body force

66
Constant Body Force
11 𝑕 = 1
21 𝑕 = 1
31 𝑕 = 1
41
1 1.00 1.00 1.00 1.00
2 1.00 1.00 1.00 1.00
3 1.00 1.00 1.00 1.00
4 1.00 1.00 1.00 1.00
5 1.3125 1.00 1.00 1.00
6 1.75 1.00 1.00 1.00
7 0.8125 1.00 1.00 1.00
8 1.00 1.00 1.00 1.00
9 1.00 1.00 1.00 1.00
10 1.00 1.3125 1.00 1.00
11 1.00 1.75 1.00 1.00
12 0.8125 1.00 1.00
13 1.00 1.00 1.00
14 1.00 1.00 1.00
15 1.00 1.3125 1.00
16 1.00 1.75 1.00
17 1.00 0.8125 1.00
18 1.00 1.00 1.00
19 1.00 1.00 1.00
20 1.00 1.00 1.3125
21 1.00 1.00 1.75
22 1.00 0.8125
23 1.00 1.00
24 1.00 1.00
25 1.00 1.00
26 1.00 1.00
27 1.00 1.00
28 1.00 1.00
29 1.00 1.00
30 1.00 1.00
31 1.00 1.00
32 1.00
33 1.00
34 1.00
35 1.00
36 1.00
37 1.00
38 1.00
39 1.00
40 1.00
41 1.00
Table 7-Effectivity indices for constant body force

67
Figure 73-The comparison of the exact and approximated solution for the constant body force
Figure 74-the stress y-y distribution for the constant body force

68
Linear Body Force
11 𝑕 = 1
21 𝑕 = 1
31 𝑕 = 1
41
1 3.75 3.75 3.75 3.75
2 1.3235 1.3235 1.3235 1.3235
3 1.117 1.117 1.117 1.117
4 1.0598 1.0598 1.0598 1.0598
5 1.5186 1.0362 1.0362 1.0362
6 2.2657 1.0242 1.0242 1.0242
7 0.9017 1.0174 1.0174 1.0174
8 1.013 1.013 1.013 1.013
9 1.0101 1.0101 1.0101 1.0101
10 1.0081 1.3969 1.0081 1.0081
11 0.9069 2.0033 1.0067 1.0067
12 0.8607 1.0055 1.0055
13 1.0047 1.0047 1.0047
14 1.004 1.004 1.004
15 1.0035 1.3651 1.0035
16 1.0031 1.9174 1.0031
17 1.0027 0.8455 1.0027
18 1.0024 1.0024 1.0024
19 1.0021 1.0021 1.0021
20 1.0019 1.0019 1.3506
21 0.9518 1.0017 1.875
22 1.0016 0.8376
23 1.0014 1.0014
24 1.0013 1.0013
25 1.0012 1.0012
26 1.0011 1.0011
27 1.001 1.001
28 1.001 1.001
29 1.0009 1.0009
30 1.0008 1.0008
31 0.9675 1.0008
32 1.0007
33 1.0007
34 1.0007
35 1.0006
36 1.0006
37 1.0006
38 1.0005
39 1.0005
40 1.0005
41 0.9755
Table 8-Effectivity indices for linear body force

69
Figure 75-The comparison of the exact and approximated solution for the linear body force
Figure 76-The stress y-y distribution for the linear body force

70
Bibliography
1. John E. Dolbow, An Extended Finite Element Method with Discontinuous Enrichment for
Applied Mechanics, Ph.D thesis, December 1999.
2. Thomas J.R. Hughes, The Finite Element Method, Linear Static and Dynamic Finite
Element Analysis, Stanford University.
3. Thomas-Peter Fries, A corrected XFEM approximation without problems in blending
elements, Int. J. Numer. Meth. Engng (2007), RWTH Aachen University, Germany.
4. N. Moes, M. Cloirec, P. Cartraud, J.-F.Remacle, A computational approach to handle
complex microstructure geometries, Comput. Methods Appl. Mech. Engrg. 192(2003)
3136-3177.
5. Stephane Bordas, Antoine Legay, X-FEM Mini-Course, EPFL, Lausanne, Switzerland,
December 2005.
6. Timon Rabczuck, Extended Finite Element Method and Meshfree Methods, Chair of
Mechanics, Bauhaus University Weimar, SS 2009.
7. N. Sukumar, D.L. Chopp, N. Moes, T. Belytschko, Modeling holes and inclusion by level
sets in the extended finite-element method, Comput. Methods Appl. Mech. Engrg. 190
(2001) 6183-6200.
8. N. Moes, J.E. Dolbow, T. Belytschko, A finite element method for crack growth without
remeshing. International Journal for Numerical Methods in Engineering 1999; 46(1):
131-150.
9. Mark Ainsworth, J. Tinsley Oden, A Posteriori Error Estimation in Finite Element Analysis,
A Willey-Interscience Publication.
10. Thomas Grätsch, Klaus-Jürgen Bathe, A posteriori error estimation techniques in
practical finite element analysis, Computers and Structures 83 (2005) 235-265.
11. T. Belytschko, N. Moes, S. Usui, and C. Parimi, Arbitrary discontinuities in finite
elements, International Journal of Numerical Methods in Engineering, vol.50, p.993-
1013, 2001.
12. T. Belytschko and T. Black, Elastic crack growth in finite elements with minimal
remeshing. International journal for numerical method in engineering 45, 601-620,
1999.
13. S. Bordas, Extended Finite Element and level set methods with applications to growth of
cracks and biofilms. Ph.D thesis, Northwestern University, December 2003.
14. J. M. Melenk and I. Babuska, The partition of unity finite element method: Basic theory
and applications. Computer Methods in Applied Mechanics and Engineering 139, 289-
314, 1996.
15. M. J. Pais, Variable amplitude fatigue analysis using surrogate models and exact XFEM
reanalysis, University of Florida, 2011.

71
16. T. Elguedj, A. Gravouil, A. Combescure, Appropriate extended function for X-FEM
simulation of plastic fracture mechanics, Comput. Methods. Appl. Mech. Engrg. 195
(2006) 501-515.
17. M. Flemming, Y. Chu, R. Moran and T. Belytschko. Enriched element free Galerkin
methods for crack tip fields. International journal for numerical methods in engineering
40, 1483-1504, 1997.
18. I. Babuska and J. M. Melenk, The partition of unity method, International journal for
numerical methods in engineering, vol40, 727-758 (1998).
19. I. Babuska and W. C. Rheinboldt, Error estimates for adaptive finite element
computations, SIAM J. Numer. Anal. 15 (4) 736-754, 1978.
20. Stephane Bordas and Marc Duflot, Derivative recovery and a posteriori error estimate
for extended finite elements, Comput. Methods Appl. Mech. Engrg. 196 (2007) 3381-
3399.
21. J. Chessa, P. Smolinski and T. Belytschko, The extended finite element method for
solidification problems, Int. J. Nummer. Meth. Engng 53:1959-1977, 2007.
22. L. N. Gifford and P. D. Hilton, Stress intensity factors by enriched finite elements.
Engineering fracture mechanics 10, 485-496, 1978.
23. J. Alberty, C. Carstensen, S. A. Funken, R. Klose, A MATLAB implementation of a finite
element method in elasticity, AMS Subject Classification: 65N30, 65R20, 73C50, 2002.
24. N. Sukumar, Z. Y. Haung, J.-H. Prevost and Z. Suo, Partition of unity enrichment for
bimaterial interface crack, Int. J. Numer. Meth. Engng 2009, 59:1075-1102, 2003.
25. N. Sukumar and J. –H. Prevost, Modelling quasi-static crack growth with the extended
finite element method part i: Computer implrmrntation. International journal of solids
and structures 40, 7513-7537, 2003.
26. O.C. Zienkiewicz, R.L. Taylor and J.Z. Zhu, The finite element method, its basis and
fundamental, Elsevier, 2005.
27. O.C. Zienkiewicz and J.Z. Zhu, The superconvergent patch recovery and a posteriori error
estimates Part 1: The recovery technique, Int. J. Numer. Methods Engrg. 33(77) 1331-
1364, 1992.
28. O.C. Zienkiewicz and J.Z. Zhu, superconvergent patch recovery and a posteriori error
estimates Part 2: error estimates and adaptivity, Int. J. Numer. Method Engrg. 33 (77)
1365-1382, 1992.
29. J. Fish and T. Belytschko, A first course in finite elements, Rensselaer Polytechnic
Institute and Northwestern University, USA, John Wiley & Sons.

Master Thesis

More Related Content

What's hot

Viewers also liked

Similar to Master Thesis

Master Thesis