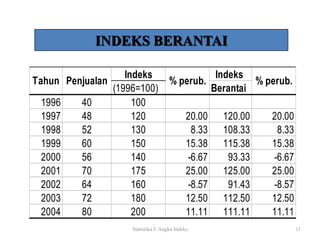
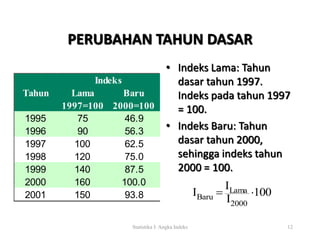
Dokumen ini menjelaskan tentang angka indeks, termasuk definisi, klasifikasi, dan berbagai tipe indeks seperti indeks sederhana, agregatif, dan agregatif tertimbang. Disebutkan juga cara menghitung masing-masing indeks dengan contoh tahun 1990 dan 2000 serta metode penimbang yang berbeda dalam indeks agregatif. Selain itu, terdapat informasi mengenai perubahan tahun dasar untuk indeks lama dan baru.

1. MODUL - 5
ANGKA INDEKS
• Indeks Sederhana
• Indeks Agregatif
• Indeks Agregatif Tertimbang
Statistika I: Angka Indeks 1

2. DEFINISI DAN KLASIFIKASI
• An index number is a percentage relative by
which a measurement in a given period is
expressed as a ratio to the measurement in
a designeted base period.
• Klasifikasi Angka Indeks:
1. Indeks Harga
2. Indeks Kuantitas
3. Indeks Nilai
Statistika I: Angka Indeks 2

3. Indeks Sederhana
• Indeks Harga (Ip): rasio antara harga tahun t (Pt)
dengan harga tahun dasar (P0) dikali 100.
100
Pt
Ip  
• Indeks Kuantitas (IQ): rasio antara kuantitas tahun
t (Qt) dengan kuantitas tahun dasar (Q0) dikali
100.
Statistika I: Angka Indeks 3
P0
100
Qt
IQ  
Q0

4. Lanjutan
• Indeks Nilai (IN): rasio
antara nilai (harga
dikali kuantitas) tahun t
(Pt.Qt) dengan nilai tahun
dasar (P0.Q0) dikali 100.
Pt 
Qt
IN 
• Tentukan Ip, IQ , IN Tahun
2000 dgn 1990 sbg. thn.
Dasar.
Tahun
1990 2000
P Q P Q
Barang
A $4 10 ton $4.50 15 ton
B 12 24 10 40
Statistika I: Angka Indeks 4
100
P0 
Q0


5. Indeks Agregatif (Komposit)
• Indeks Harga Agregatif (Ip): rasio antara harga tahun t
(Pt) dengan harga tahun dasar (P0) yang meliputi
beberapa macam produk dikali 100.
100
Pt

Ip 
• Indeks Kuantitas Agregatif (IQ): rasio antara kuantitas
tahun t (Qt) dengan kuantitas tahun dasar (Q0) yang
meliputi beberapa macam produk dikali 100.
Qt

IQ 
Statistika I: Angka Indeks 5
P0


100
Q0



6. Lanjutan . . .
• Indeks Nilai Agregatif (IN): rasio
antara nilai produk tahun t
(Pt.Qt) dengan nilai produk
tahun dasar (P0.Q0) yang
meliputi beberapa macam
produk dikali 100.
100
Pt Qt
  
IN 
 
• Tentukan Ip, IQ , IN Tahun
2000 dgn 1990 sbg. thn.
Dasar meliputi 2 mcm brg.
Tahun
1990 2000
P Q P Q
Barang
A $4 10 ton $4.50 15 ton
B 12 24 10 40
Statistika I: Angka Indeks 6
P0 Q0

7. Indeks Agregatif Tertimbang
• Formula indeks agregatif tertimbang:
100
Pt
  
w
I 
 
• Formulas Laspeyres: kuantitas tahun dasar (Q0)
sebagai penimbang.
Pt Q0
  
IL 
 
Statistika I: Angka Indeks 7
P0
w
w
100
P0 Q0

8. Lanjutan
• Formula Paasche: kuantitas tahun t (Qt)
sebagai penimbang.
100
Pt Qt
  
IP 
 
P0 Qt
• Formula Fisher: akar perkalian IL dan IP.
100
IP


IF  
100
IL
 
100
Statistika I: Angka Indeks 8



9. Lanjutan
• Formula Marshal-Edgeworth: penjumlahan
kuantitas tahun t (Qt) dan kuantitas tahun
dasar (Q0) sebagai penimbang.
100
Pt (Qt Q0)
   
IME 
  
P0 (Qt Q0)
• Formula Drobisch: penjumlahan IL dan IP
dibagi 2.
IL IP
2
Statistika I: Angka Indeks 9
ID



10. Lanjutan
• Formula Walsh: akar
perkalian kuantitas
tahun t (Qt) dan kuan-titas
tahun dasar (Q0)
sebagai penimbang.
   
P0 (Qt Q0)
• Tentukan: IL, IP, IF,
IME, ID, IW.
Tahun
1990 2000
P Q P Q
Barang
A $4 10 ton $4.50 15 ton
B 12 24 10 40
100
Statistika I: Angka Indeks 10
Pt (Qt Q0)
IW 
  

11. INDEKS BERANTAI
Indeks Indeks
Tahun Penjualan % perub. % perub.
(1996=100) Berantai
1996 40 100
1997 48 120 20.00 120.00 20.00
1998 52 130 8.33 108.33 8.33
1999 60 150 15.38 115.38 15.38
2000 56 140 -6.67 93.33 -6.67
2001 70 175 25.00 125.00 25.00
2002 64 160 -8.57 91.43 -8.57
2003 72 180 12.50 112.50 12.50
2004 80 200 11.11 111.11 11.11
Statistika I: Angka Indeks 11

12. PERUBAHAN TAHUN DASAR
Indeks
Lama Baru
1997=100 2000=100
Tahun
1995 75 46.9
1996 90 56.3
1997 100 62.5
1998 120 75.0
1999 140 87.5
2000 160 100.0
2001 150 93.8
• Indeks Lama: Tahun
dasar tahun 1997.
Indeks pada tahun 1997
= 100.
• Indeks Baru: Tahun
dasar tahun 2000,
sehingga indeks tahun
2000 = 100.
Baru  
100
I
Lama
I
I
2000
Statistika I: Angka Indeks 12