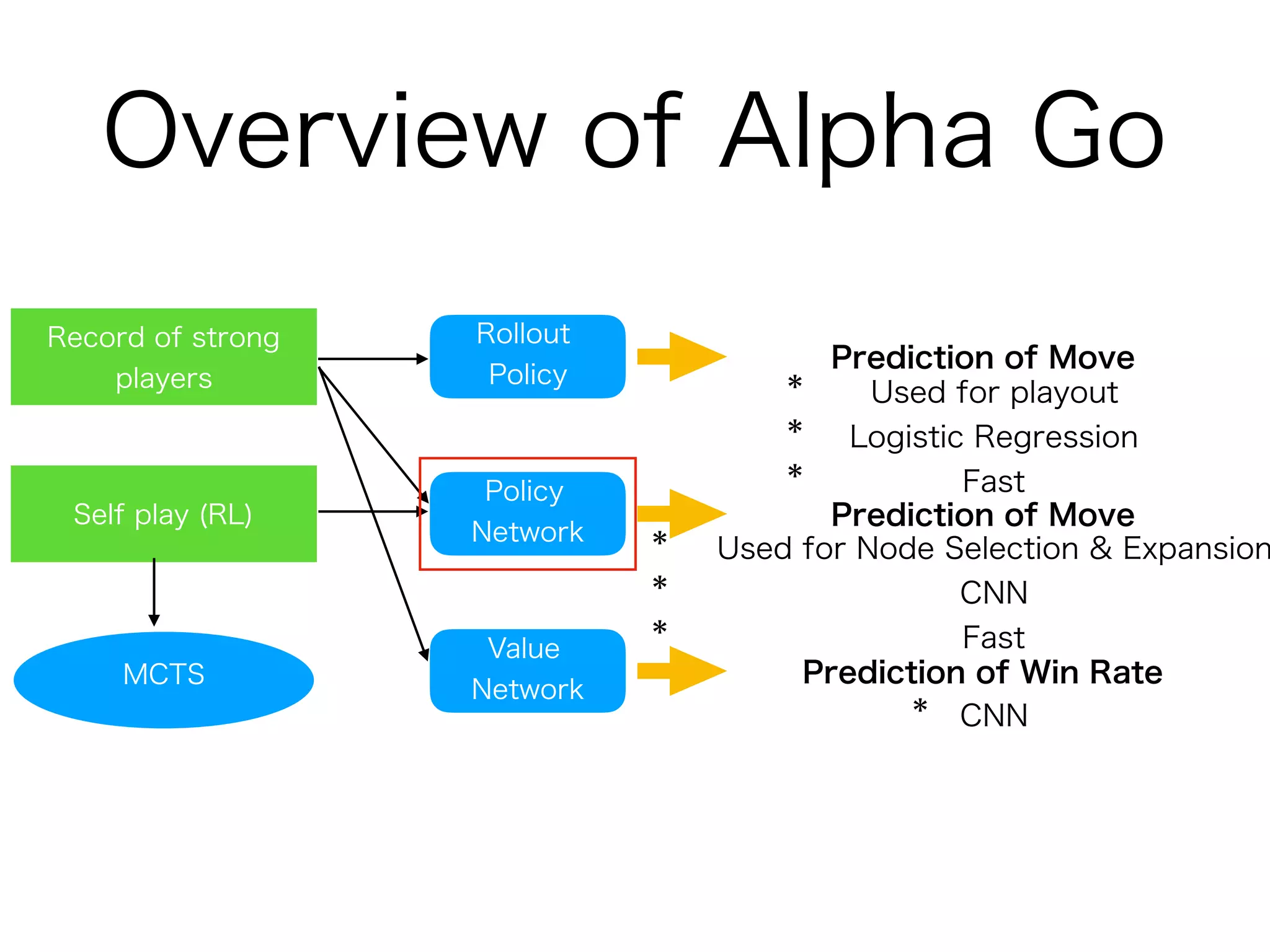
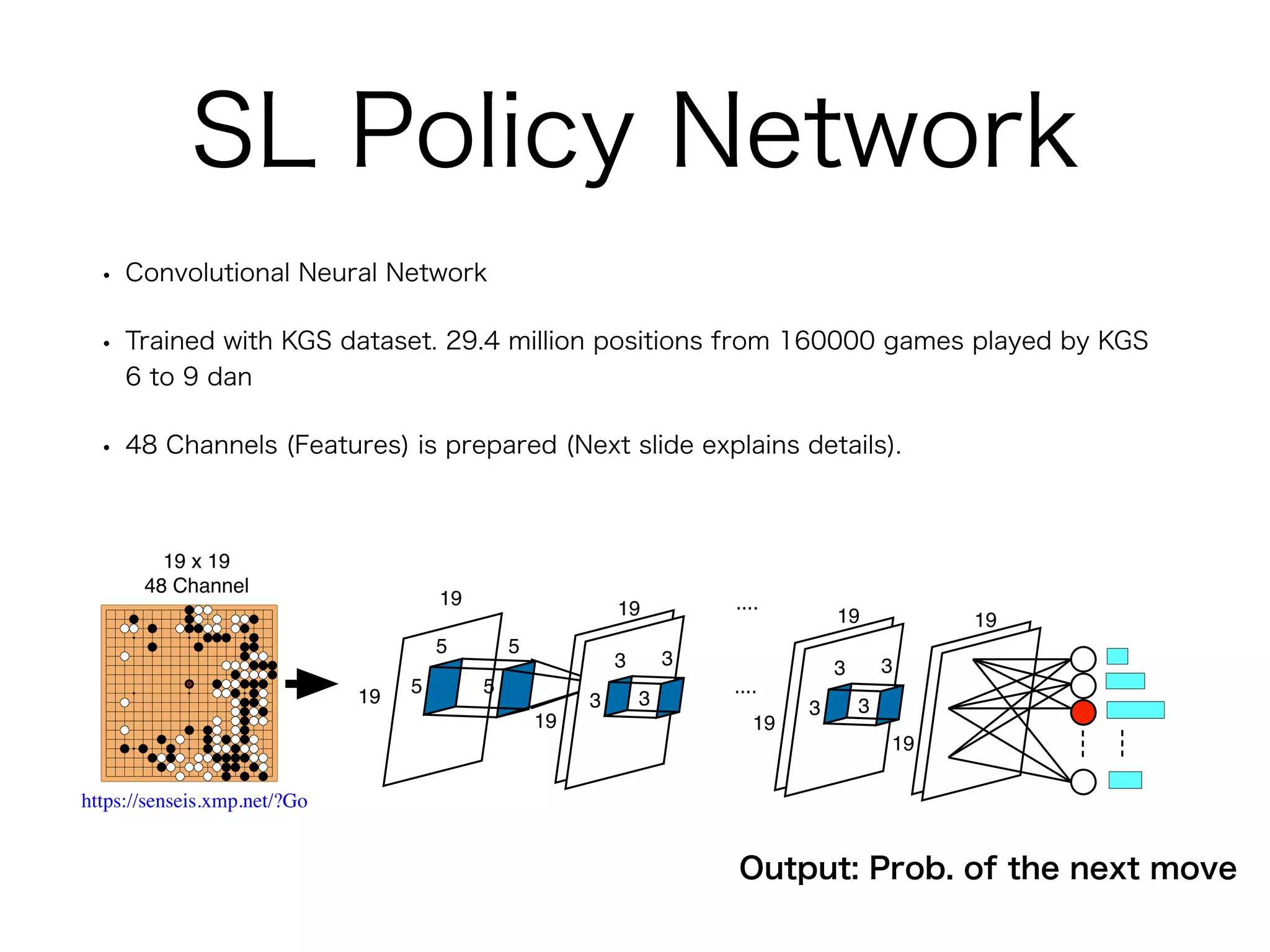
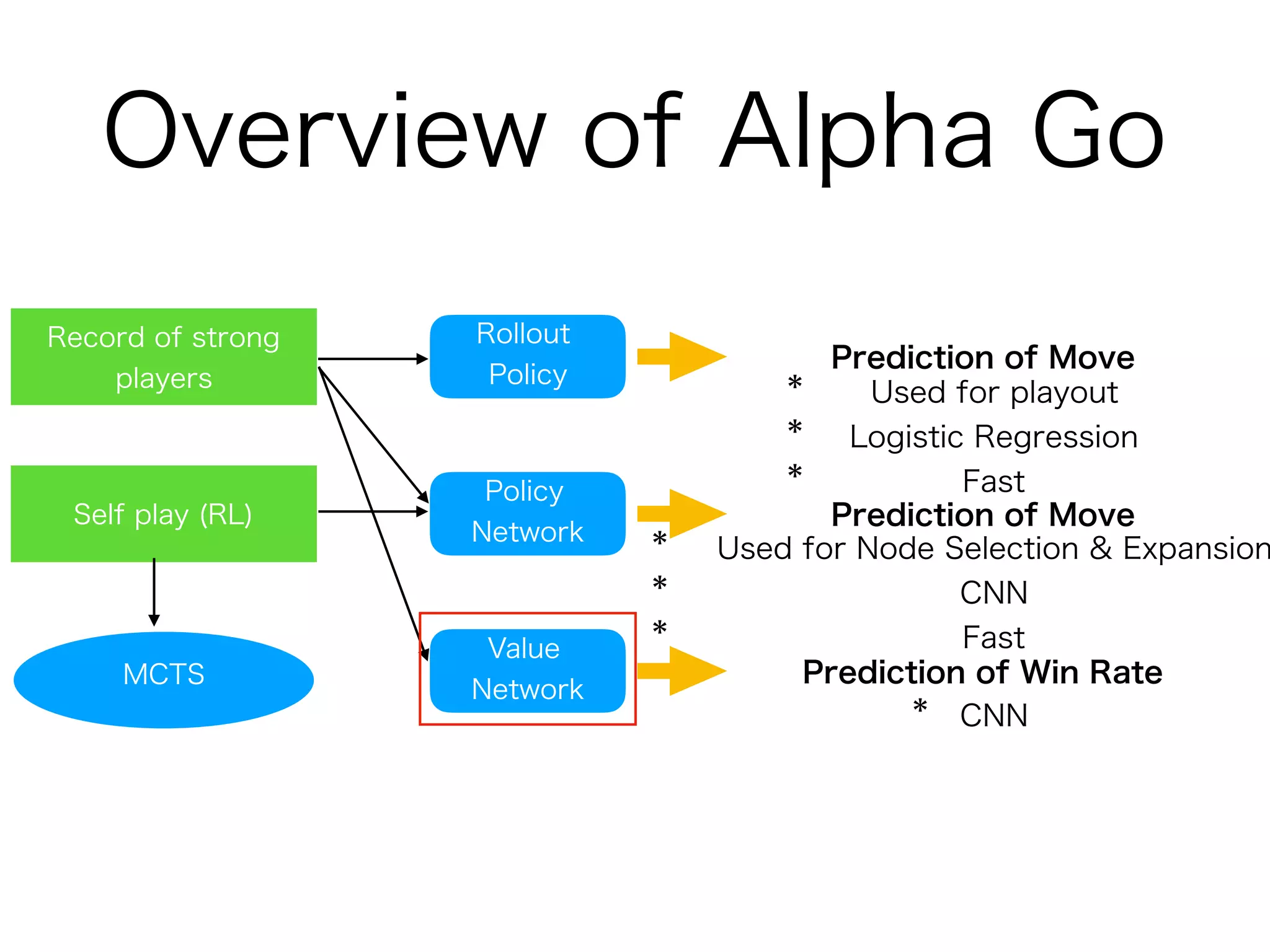
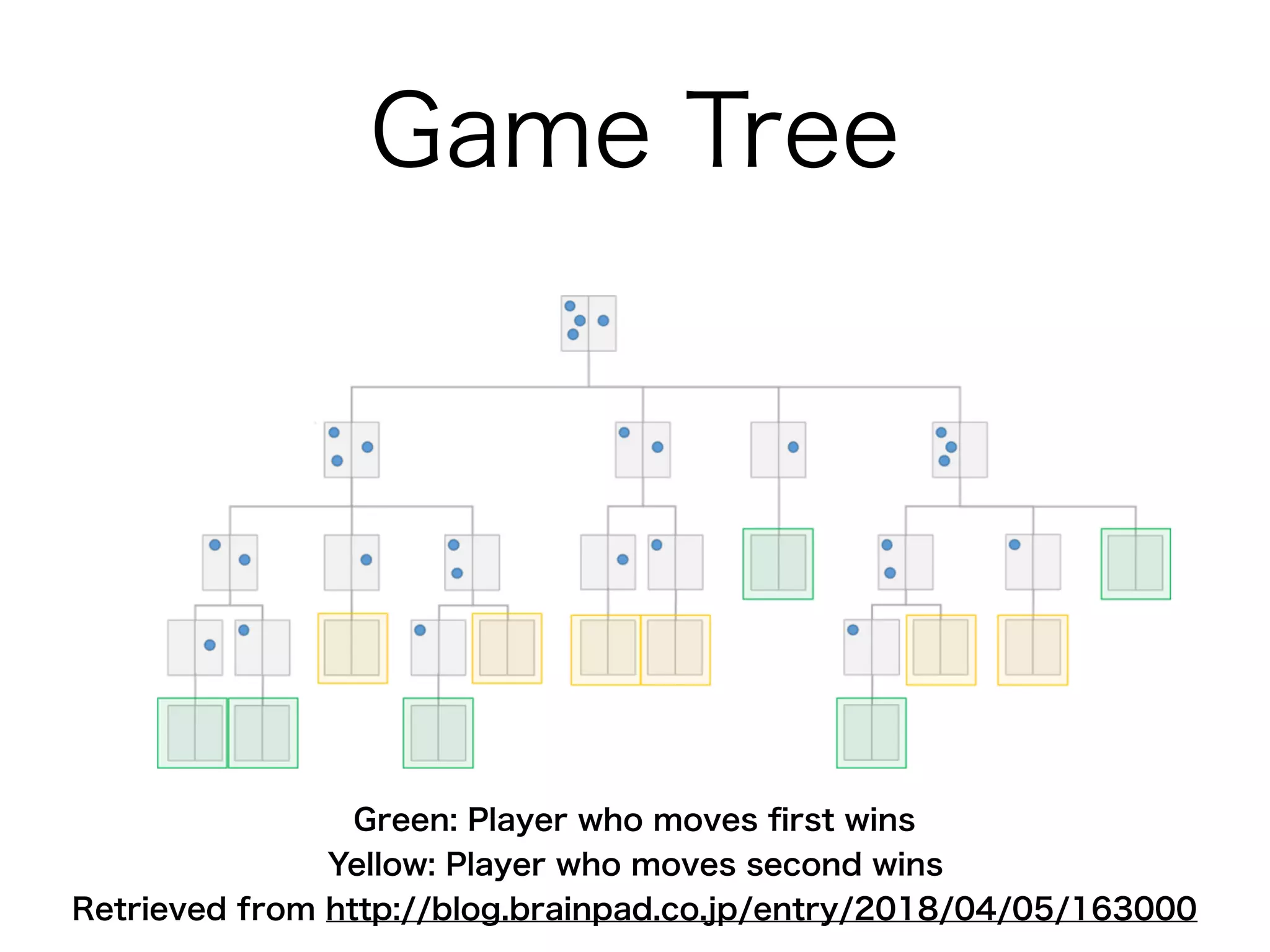
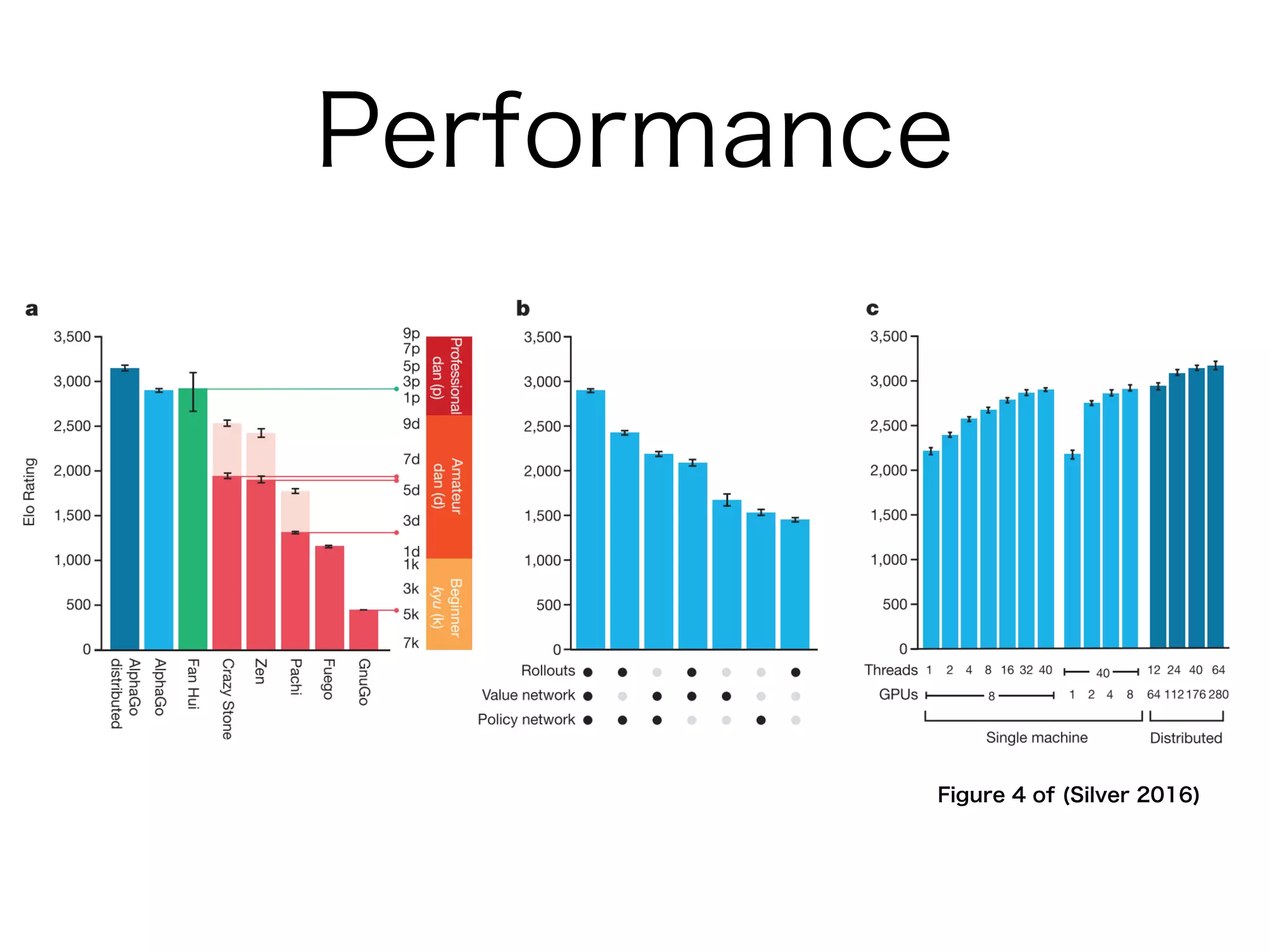
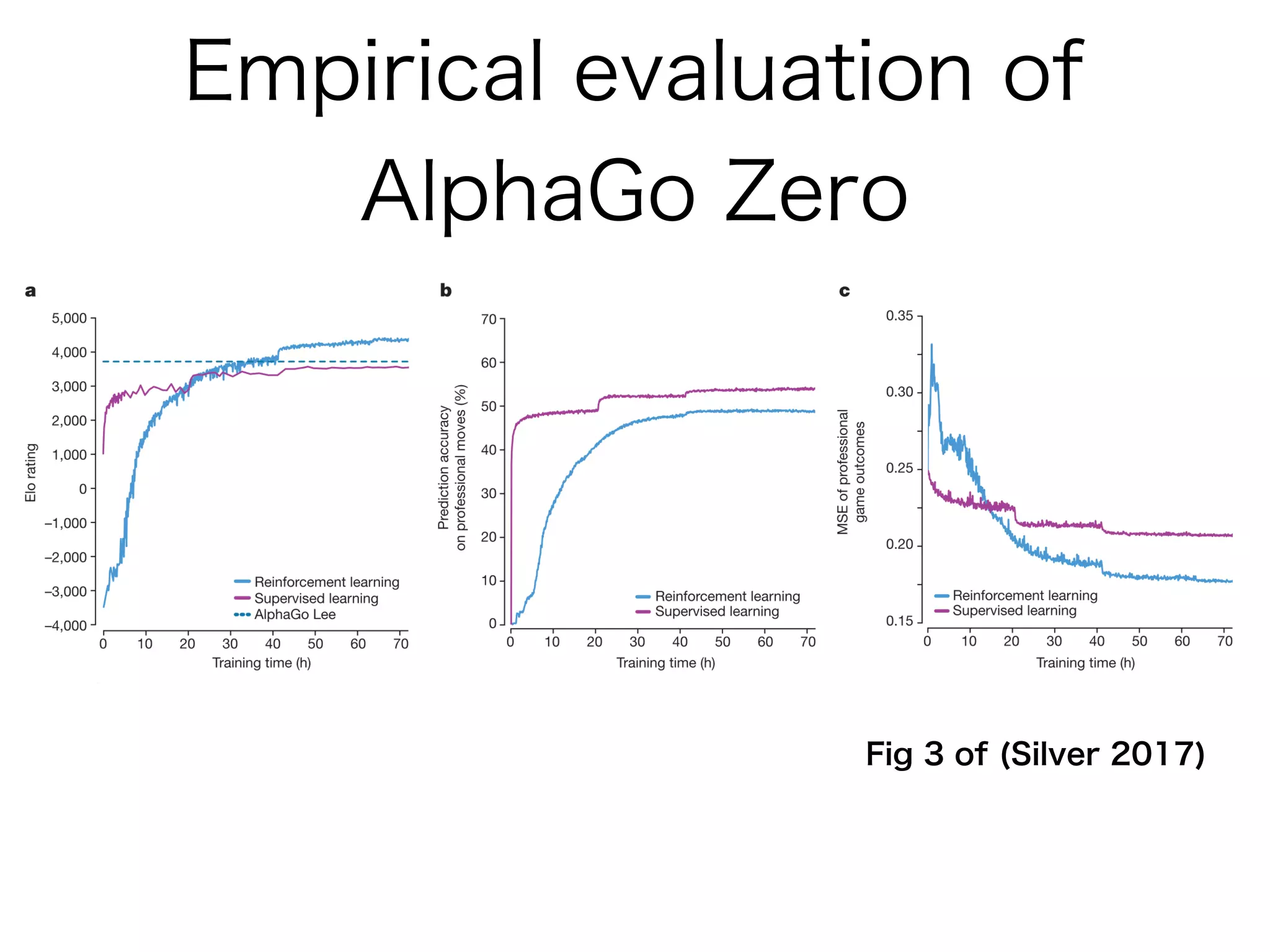
AlphaGo Zero is an AI agent created by DeepMind to master the game of Go without human data or expertise. It uses reinforcement learning through self-play with the following key aspects:
1. It uses a single deep neural network that predicts both the next move and the winner of the game from the current board position. This dual network is trained solely through self-play reinforcement learning.
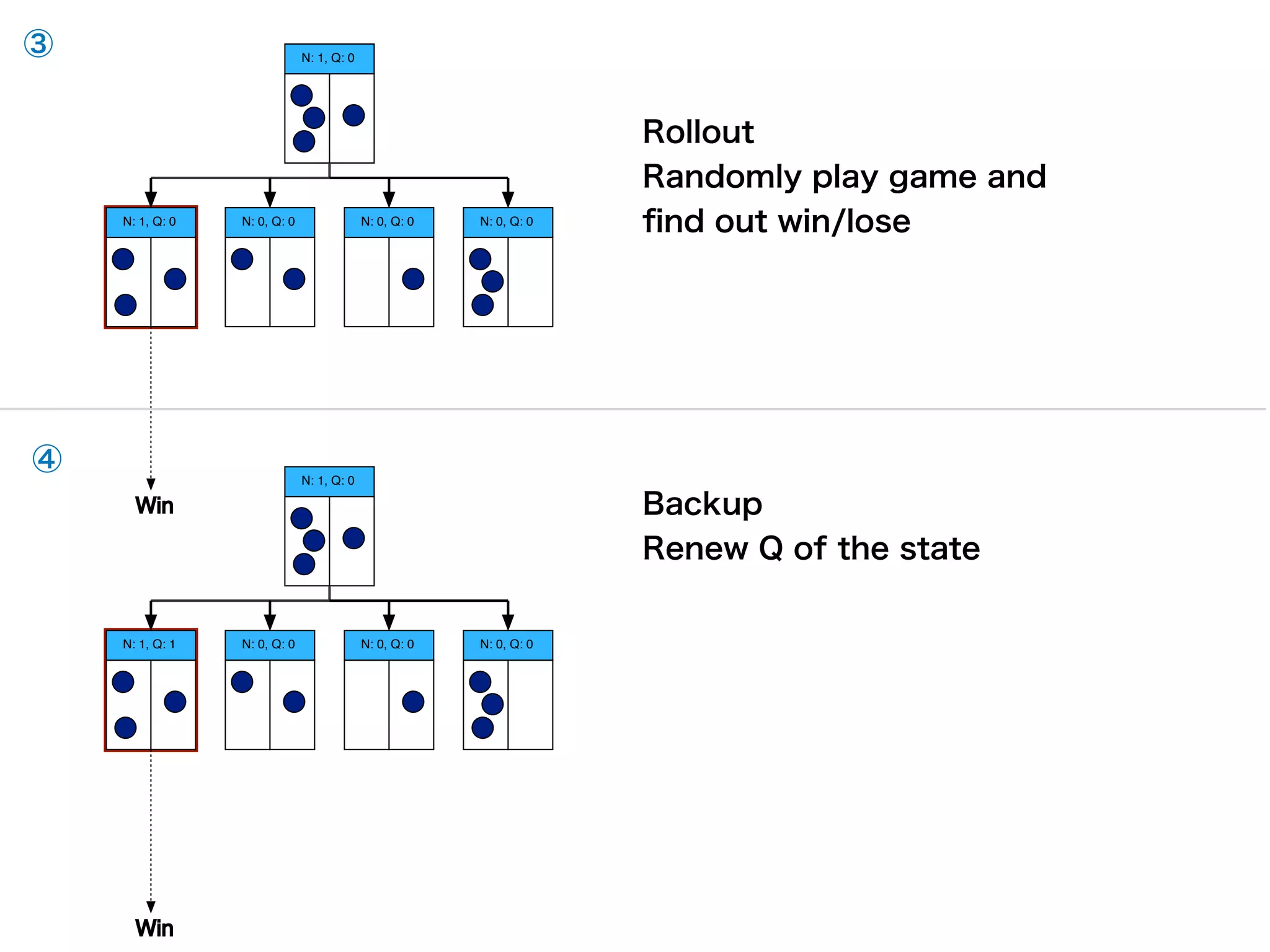
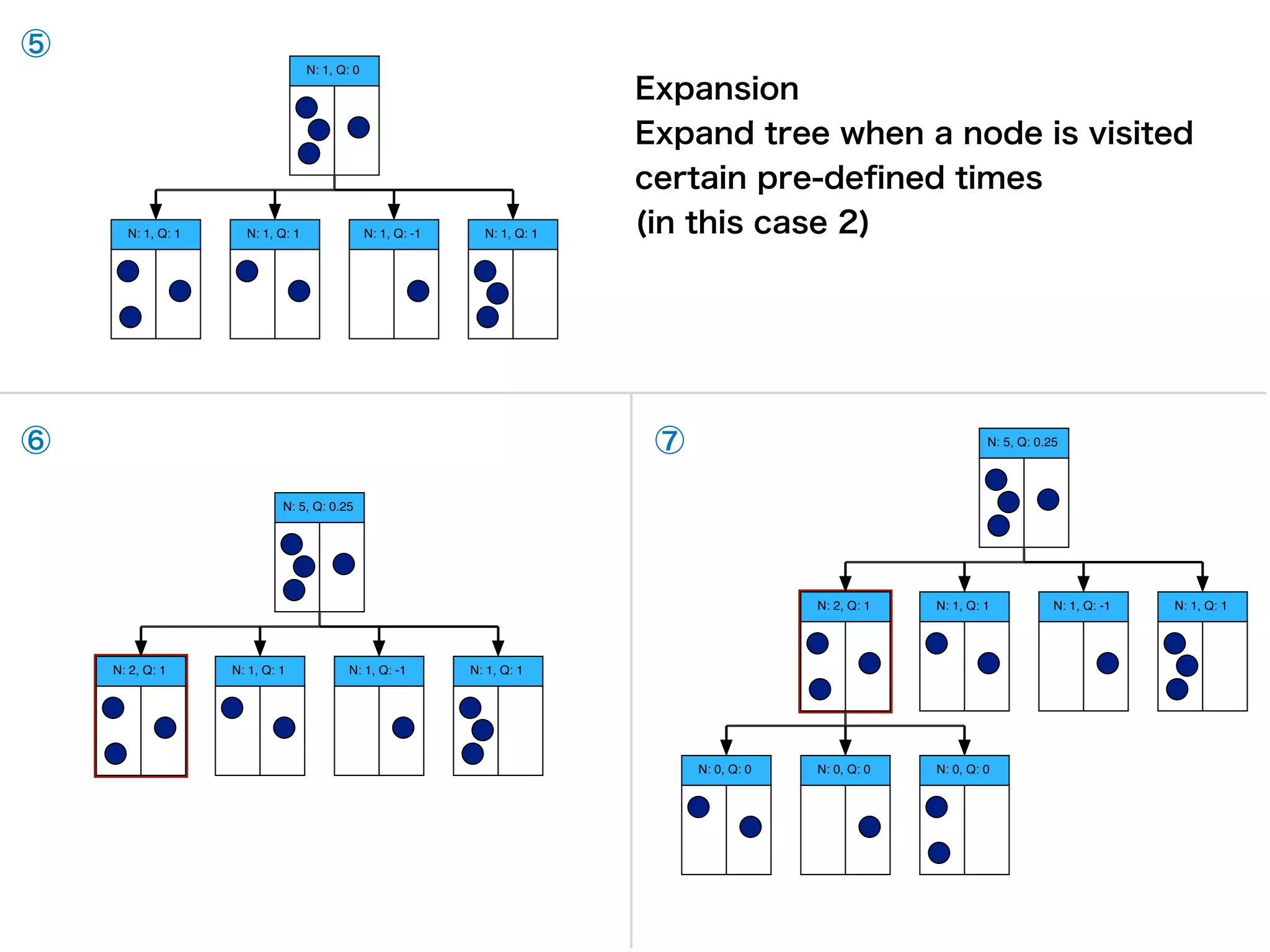
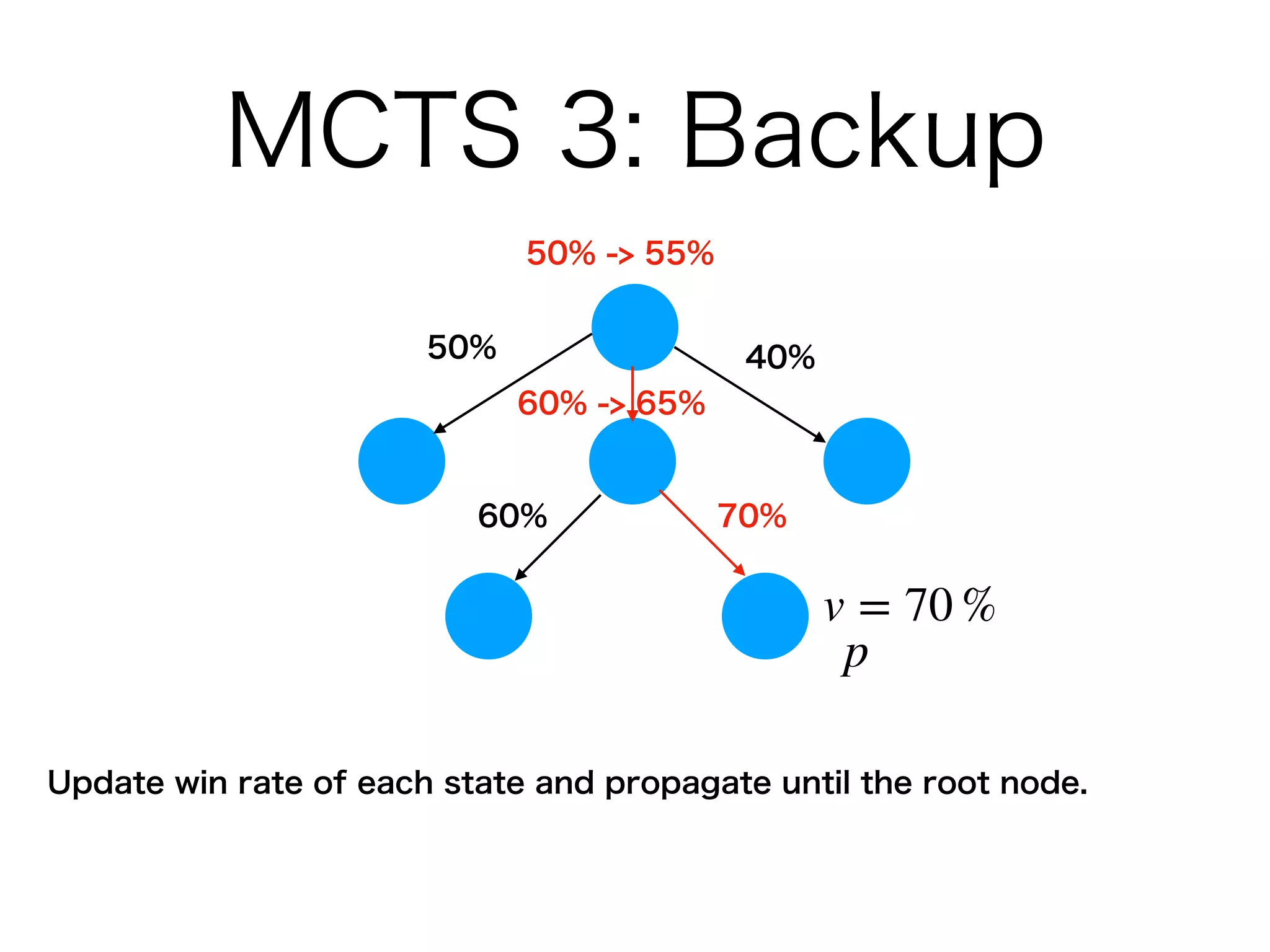
2. The neural network improves the Monte Carlo tree search used to select moves. The search uses the network predictions to guide selection and backup of information during search.
3. Training involves repeated self-play games to generate data, then using this data to update the neural network parameters through gradient descent. The updated network plays