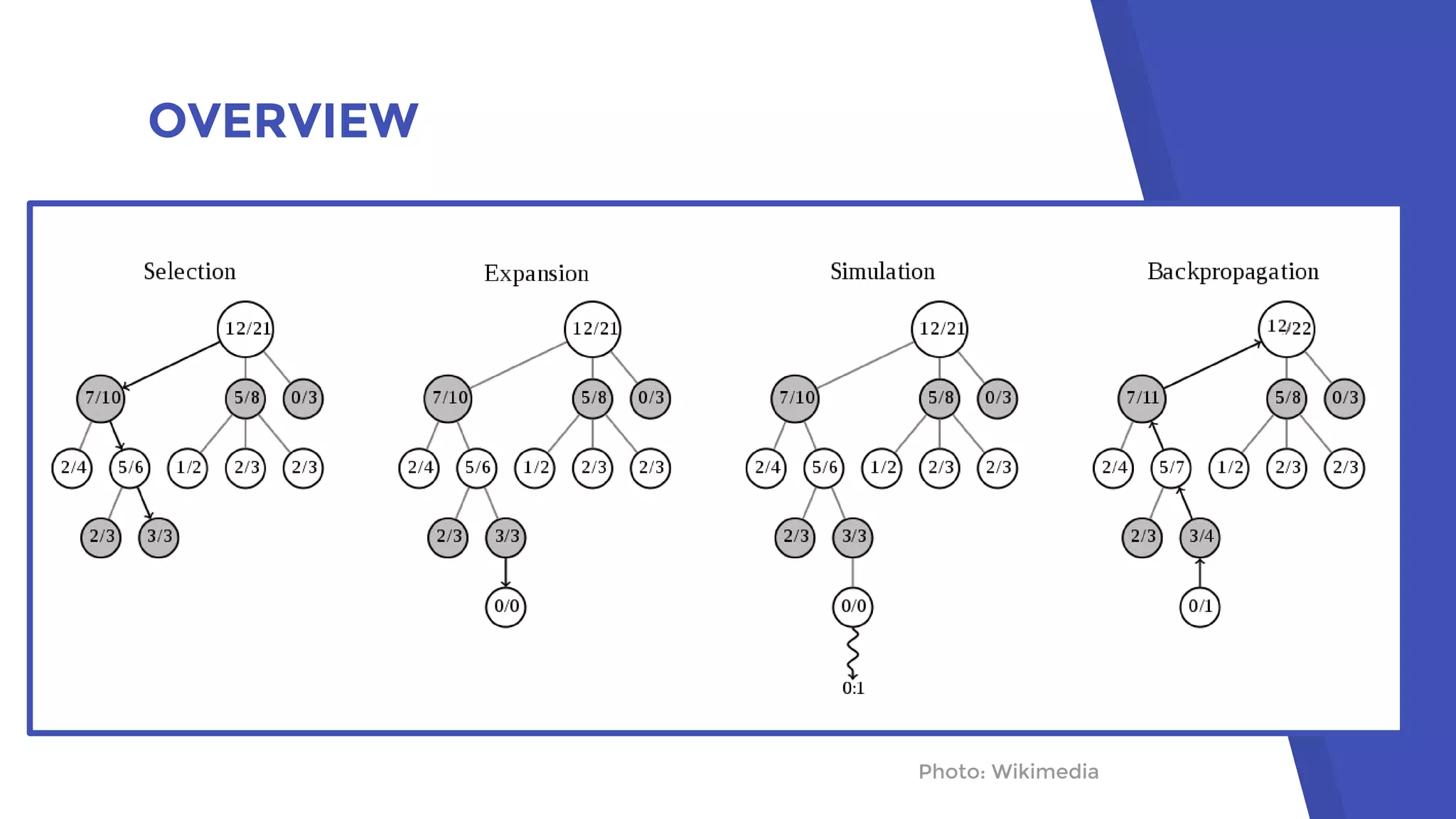
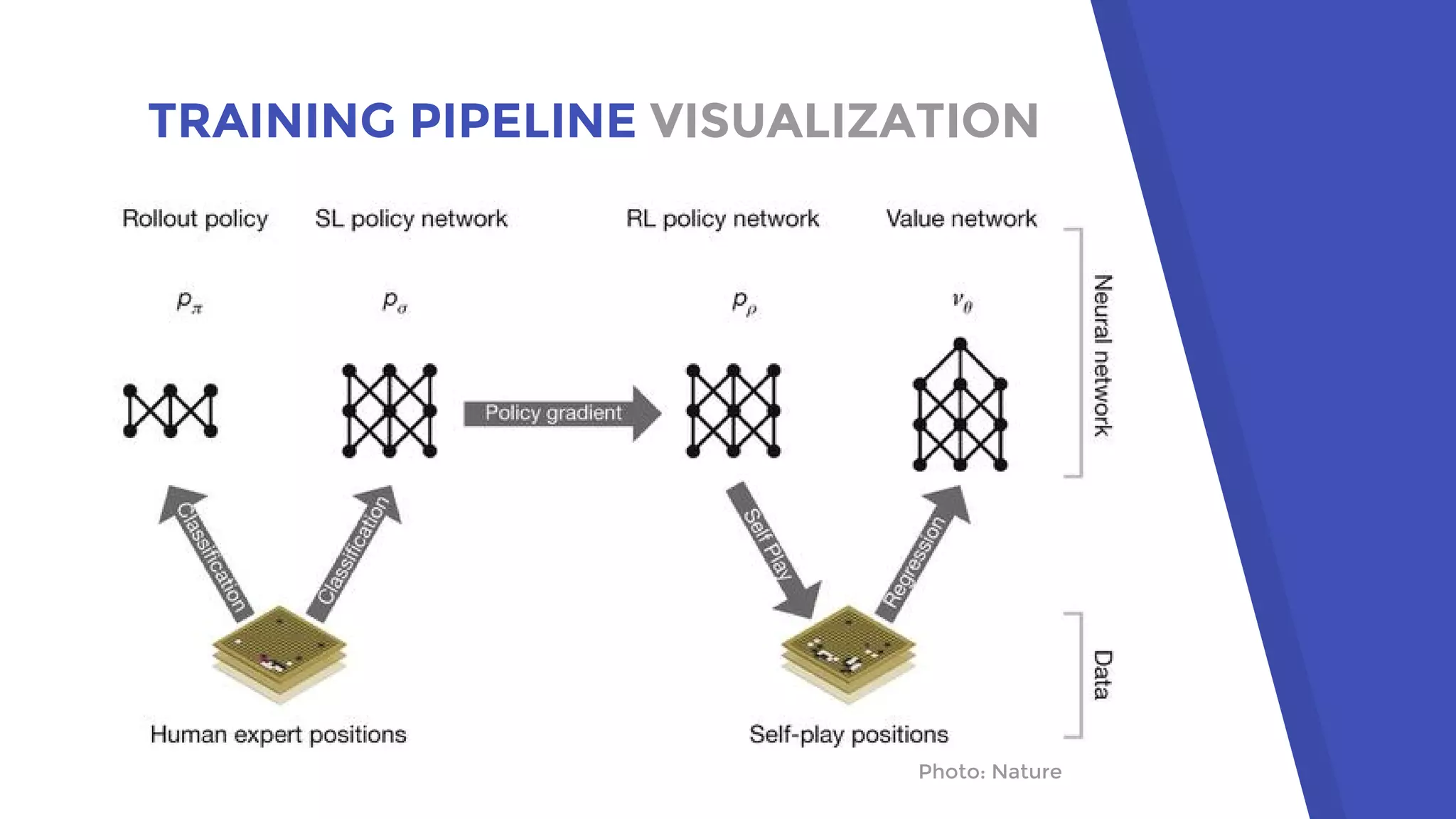
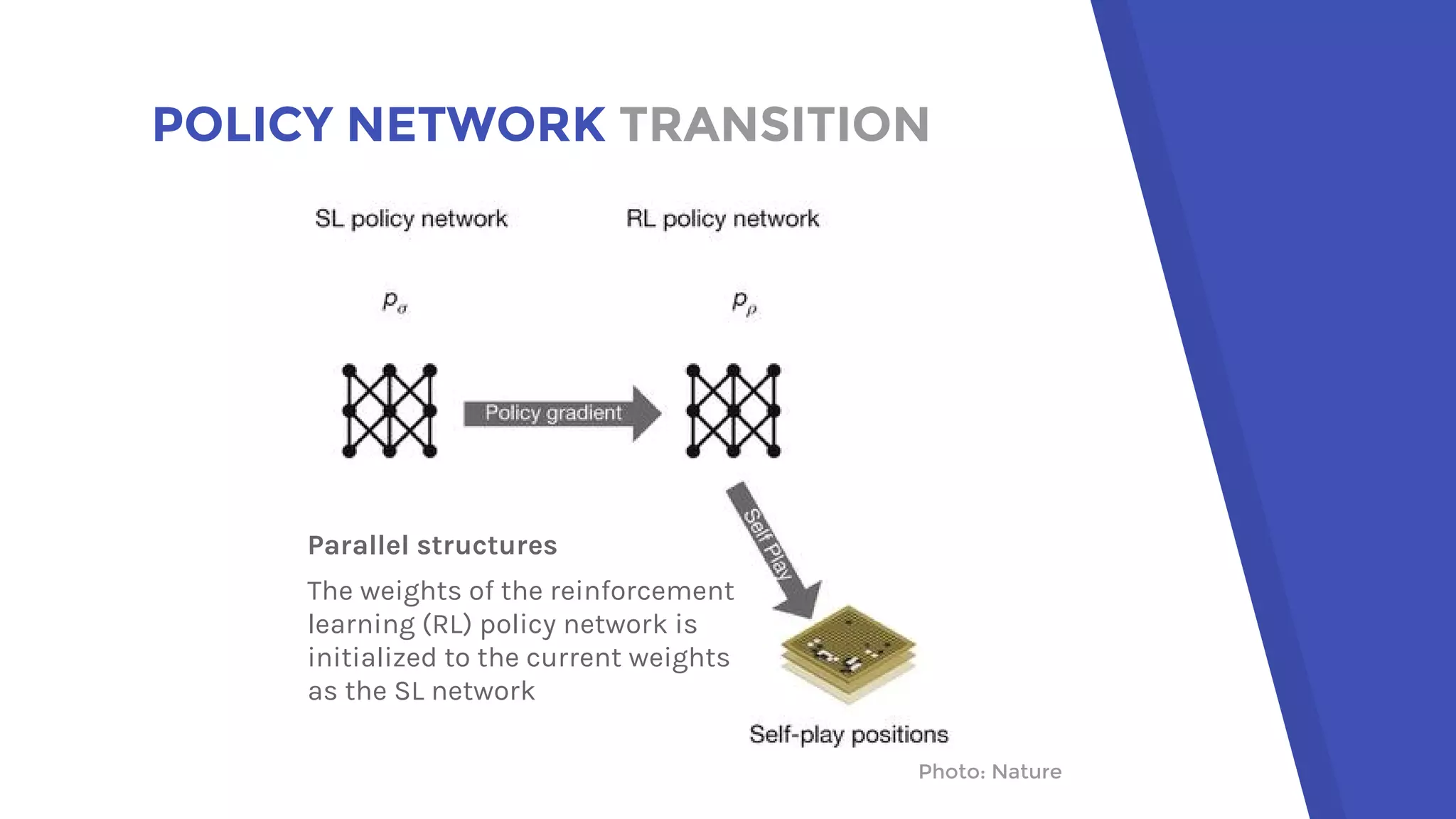
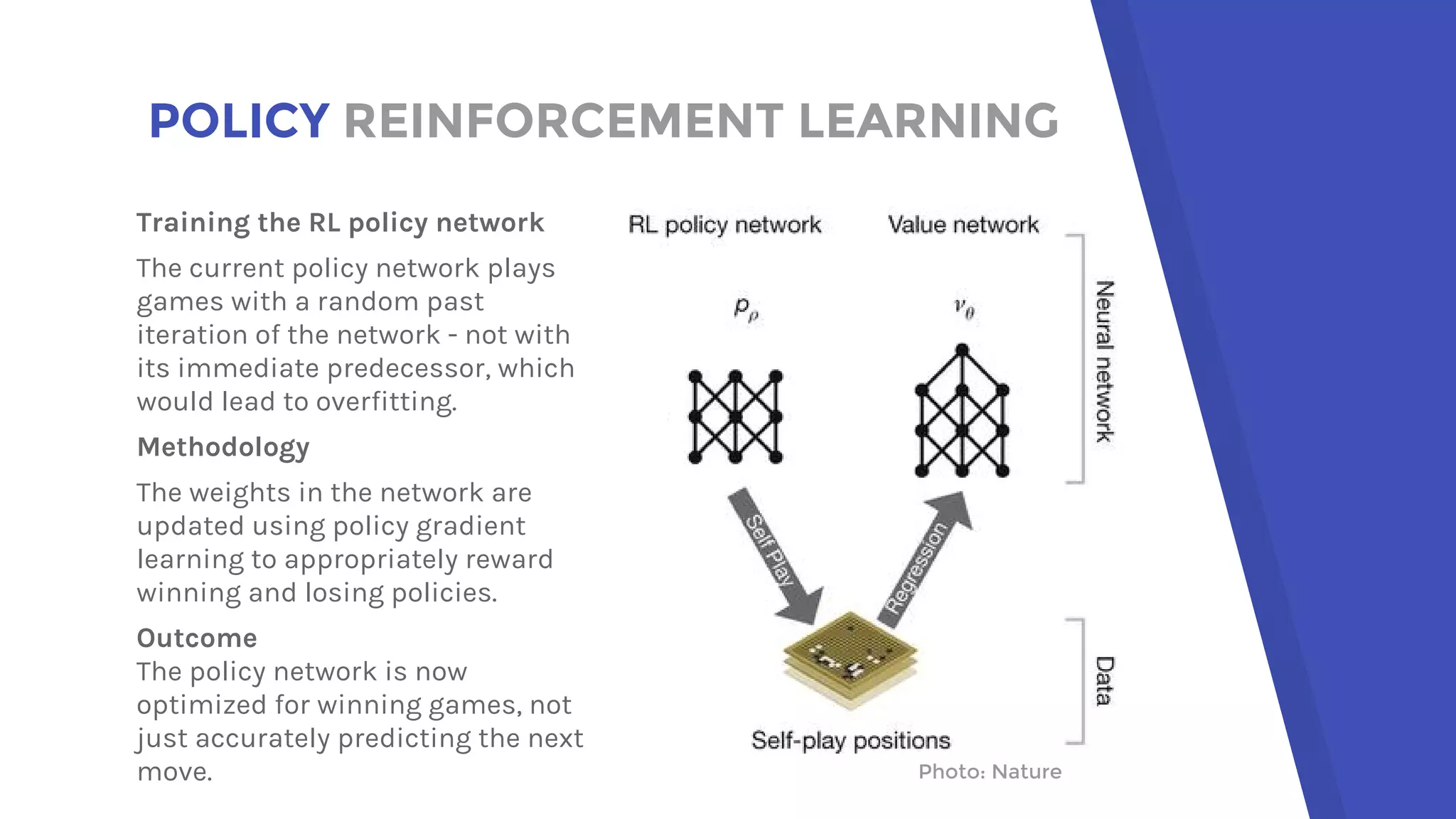
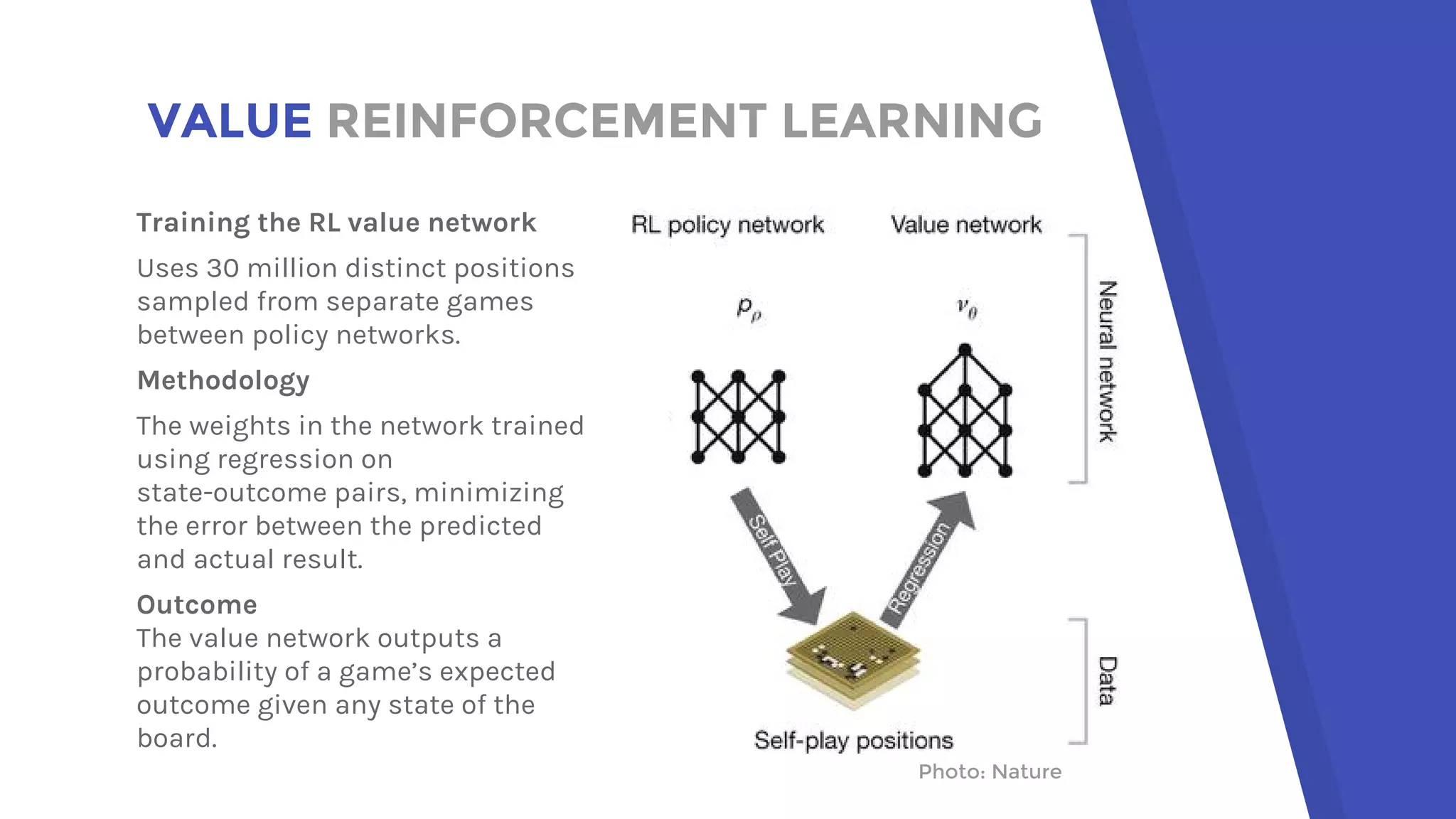
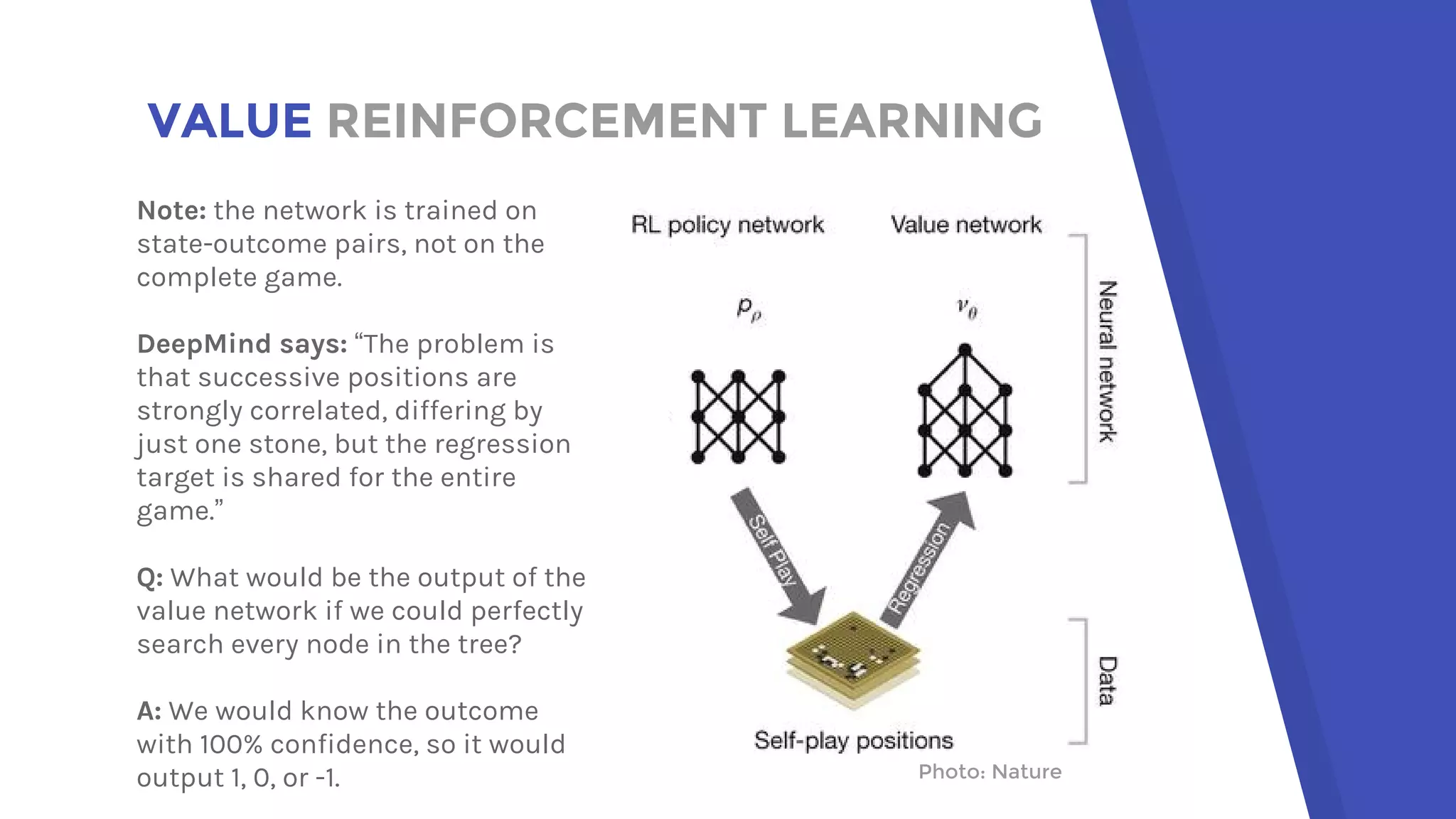
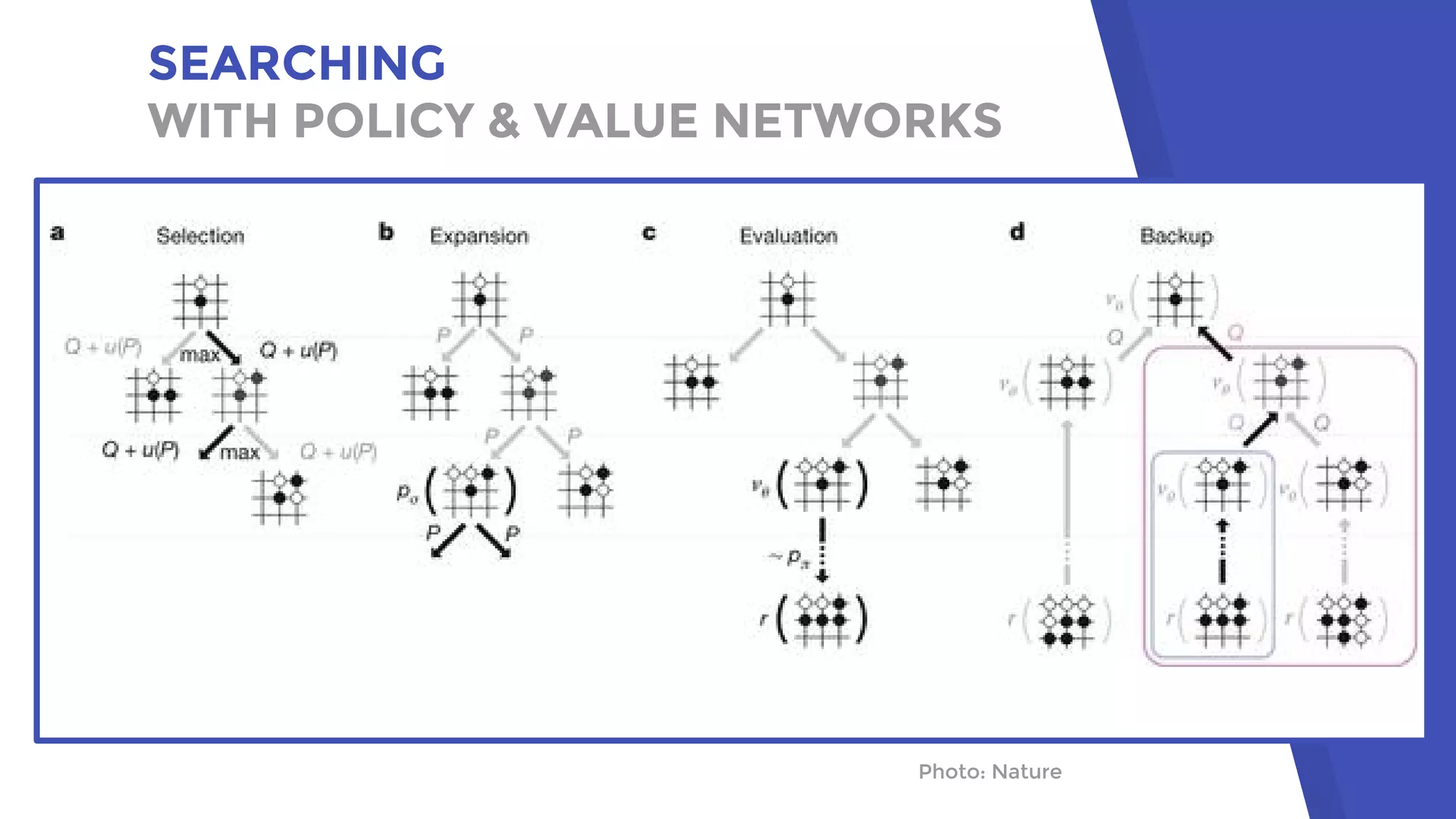
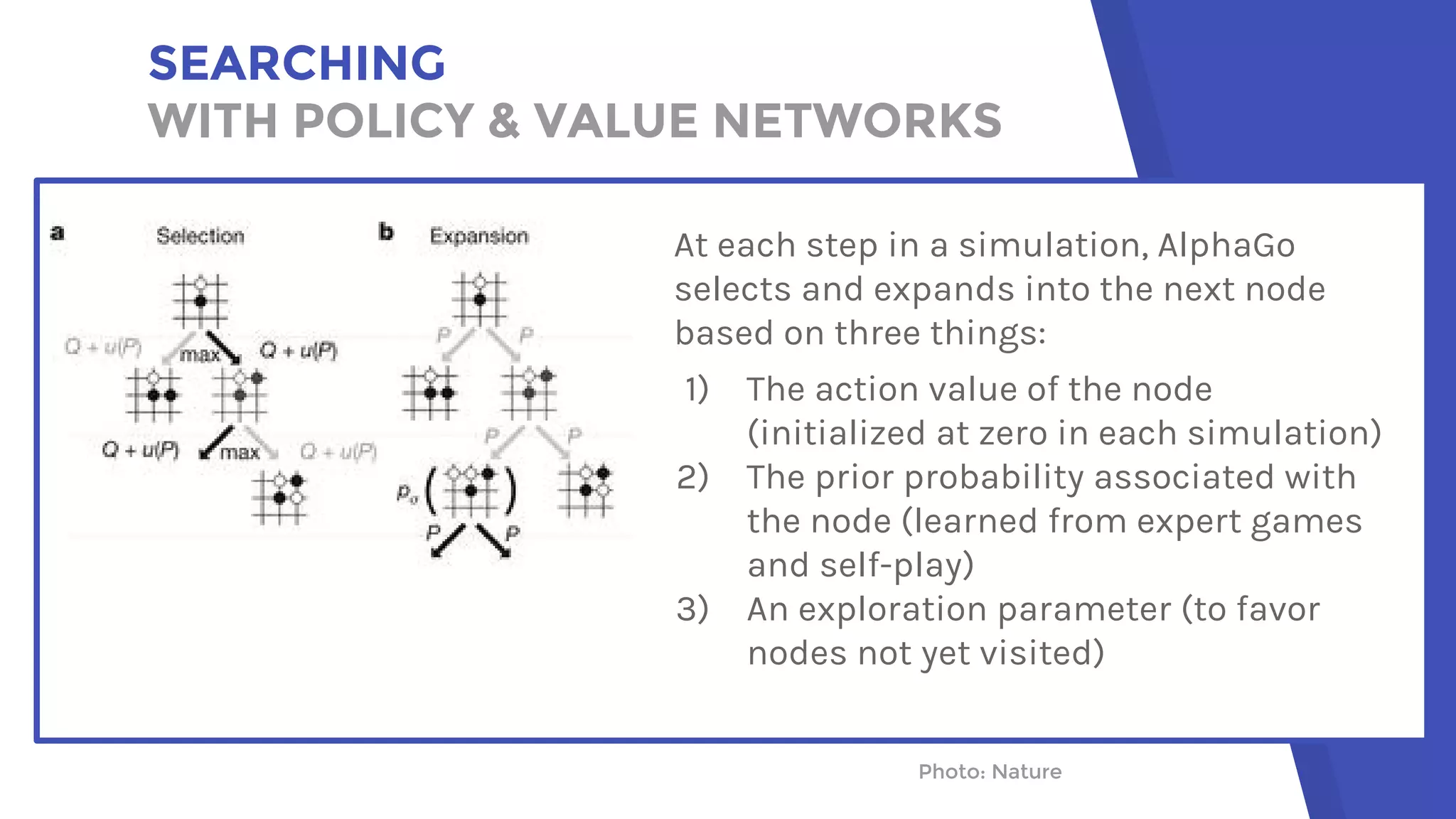
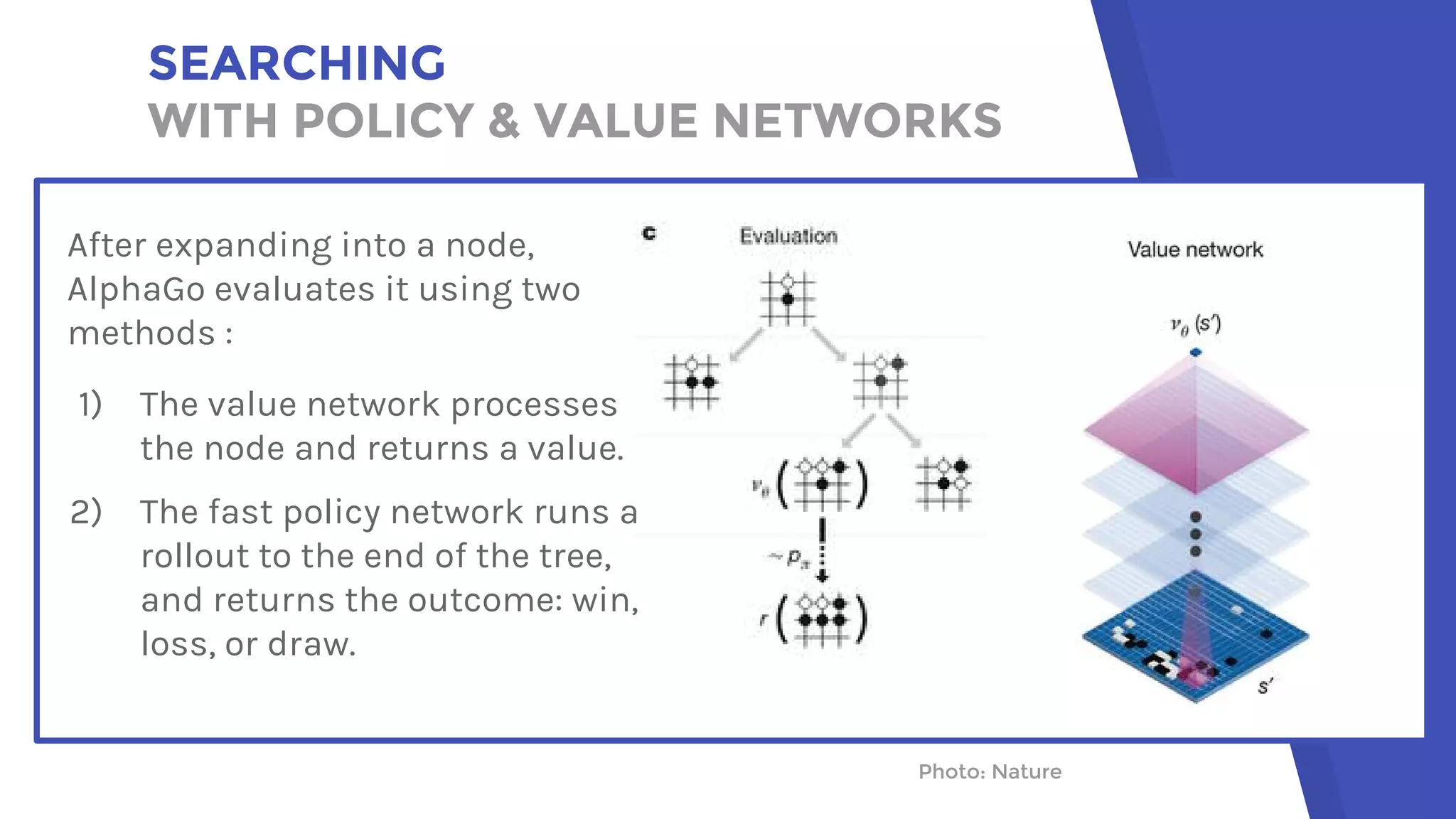
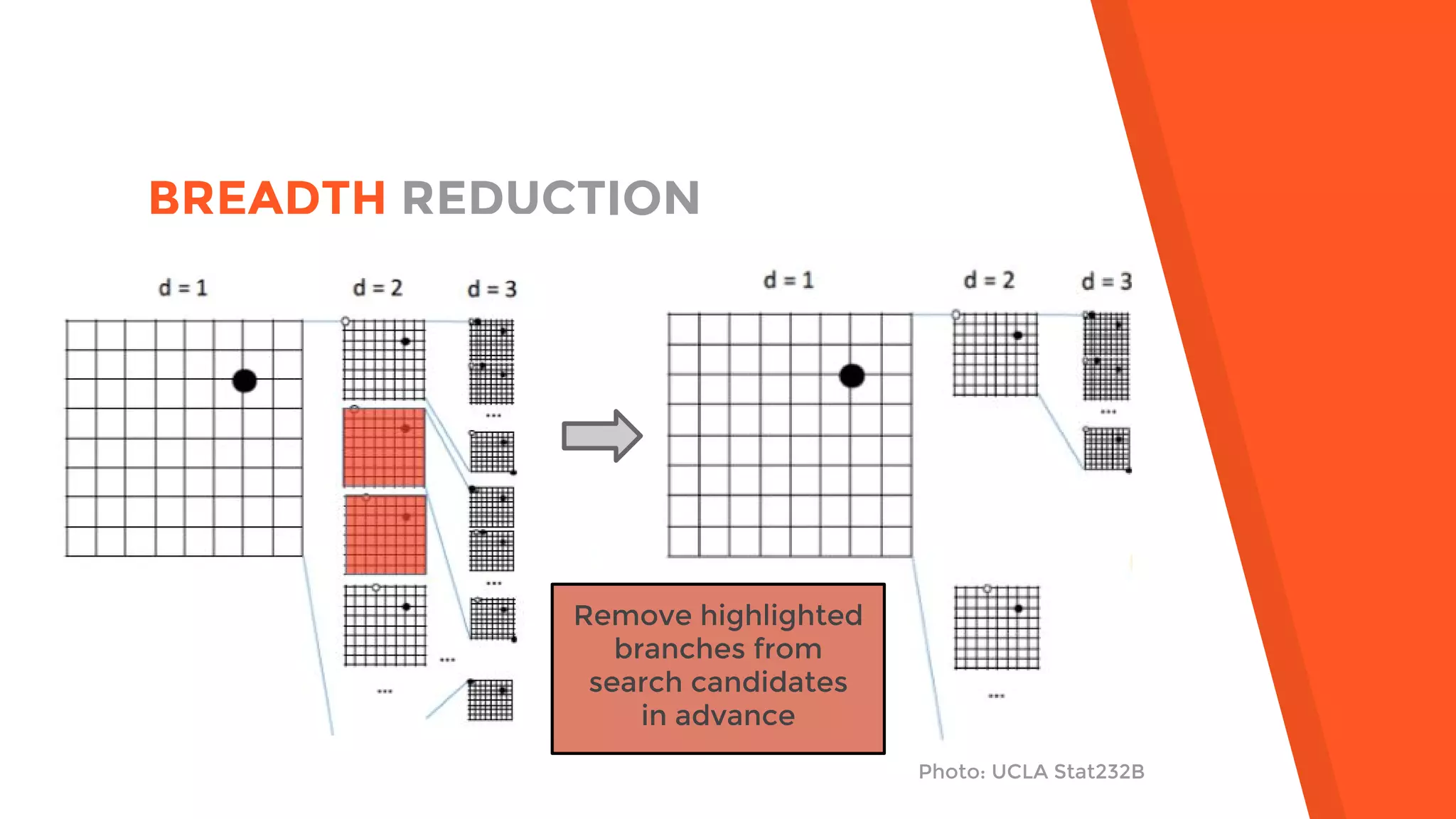
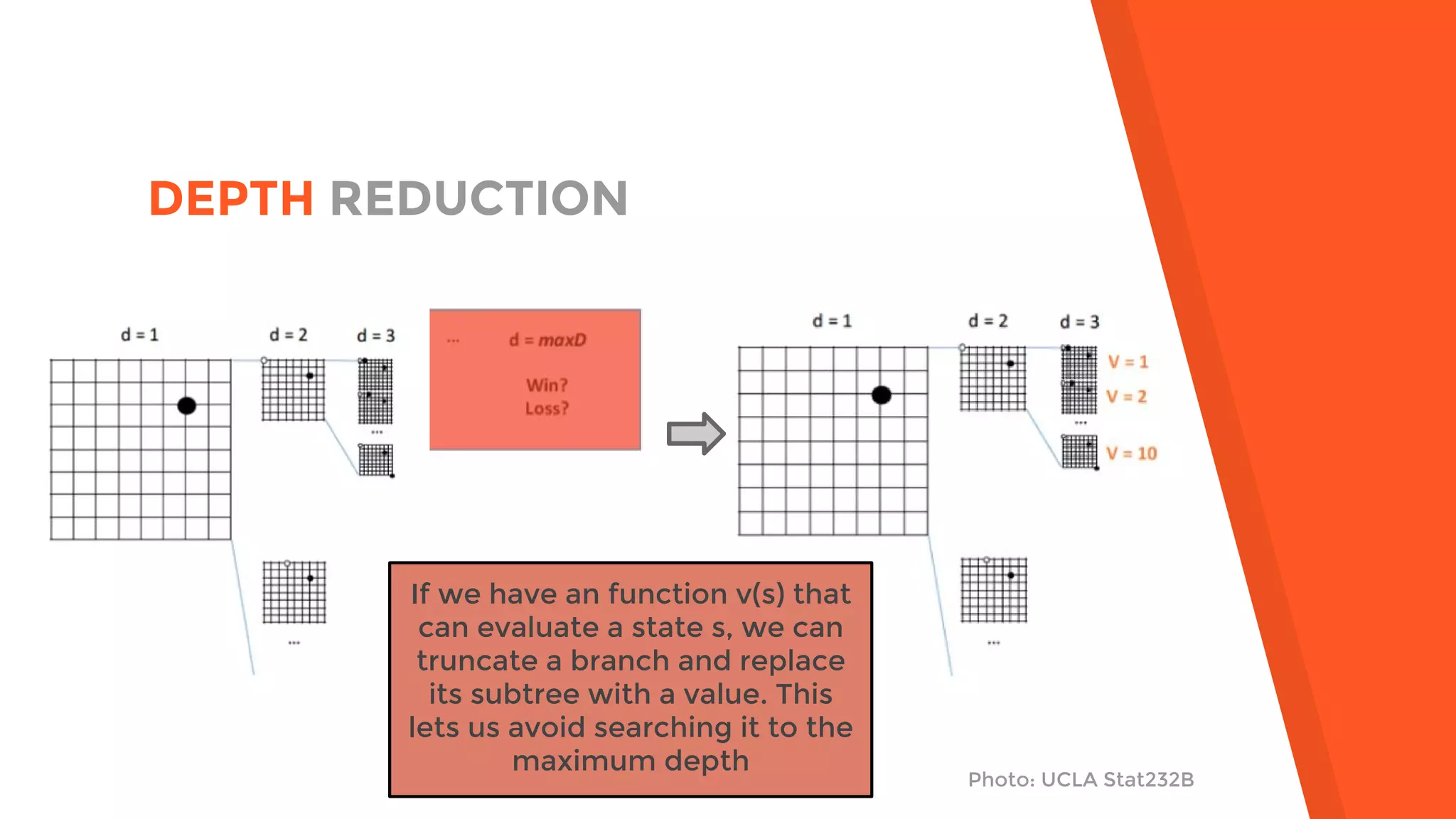
AlphaGo uses a novel combination of Monte Carlo tree search and neural networks to master the game of Go. It trains two neural networks - a policy network to predict expert moves and a value network to evaluate board positions. During gameplay, AlphaGo runs multiple Monte Carlo tree simulations that use the neural networks to guide search and evaluate positions. The move selected is the one most frequently visited after all simulations. This approach allowed AlphaGo to defeat world champion Lee Sedol 4-1, achieving a milestone in artificial intelligence.












![SURVEY OF AI GAMING MILESTONES
1914 Torres y Quevedo built a device that played a limited chess endgame
1950 Claude Shannon writes “Programming a Computer to Play Chess”
1952 Alan Turing writes a chess program (with no computer to run it!)
1968 Alfred Zobrist’s Go program beats total beginners [minimax tree search]
1979 Bruce Wilson’s Go program beats low-level amateurs [knowledge systems]
1980 Moor plays the world Othello champion (1-5)
1994 Chinook plays the world checkers champion (2-4-33)
1997 Deep Blue plays Gary Kasparov at chess (2-1-3)
2006 “The year of the Monte Carlo revolution in Go” - Coulum discovers MCTS
2011 IBM Watson plays Ken Jennings at Jeopardy ($77,147 - $24,000)
2013 Crazy Stone beats a handicapped Go pro player [Monte Carlo tree search]
2015 AlphaGo beats the European Go champion Fan Hui (5-0) [neural networks]
2016 AlphaGo beats the Go world champion Lee Sedol (4-1)](https://image.slidesharecdn.com/howdeepmindmasteredthegameofgo-160903224536/75/How-DeepMind-Mastered-The-Game-Of-Go-15-2048.jpg)