This document discusses fuzzy sets and their basic concepts and operations. It begins by defining fuzzy sets and their membership functions, which assign a degree of membership between 0 and 1 to each element of a universal set, unlike crisp sets which only assign 0 or 1. It then discusses α-cut sets, which are crisp sets of elements with membership above a given value α. Other concepts covered include convex fuzzy sets, fuzzy numbers representing intervals, and the magnitude and subsets of fuzzy sets. Standard fuzzy set operations like complement, union, intersection and difference are also defined. Finally, fuzzy relations and their composition are introduced.






![CHAPTER 1 FUZZY SETS
1
Chapter (1)
FUZZY SETS
In this chapter, we will define basic operations on fuzzy sets. Each fuzzy
set A is defined in terms of a relevant classical set, X , by a function
analogous to the characteristic functions, called a membership function,
assign to each element x of X a number, x , in the closed unit interval I
that characterizes the degree of membership of x in A.
1.1Definition of fuzzy set
1.1.1 Expression for fuzzy set
Membership function A
in crisp set maps whole in universal set X to
set {0, 1}.
}1,0{: X
A
Definition 1.1 (Member function of fuzzy set) in fuzzy sets, each
element is mapped to [0, 1] by membership function
]1,0[: X
A
where [0, 1] means real numbers between 0 and 1 (including 0,
1).Consequently, fuzzy set is ‘vague boundary set’ comparing with
crisp set.
1.1.2 Expansion of fuzzy set
Definition 1.2 (type-n fuzzy set) the value of membership degree might
include uncertainty. If the value of membership function is
given by a fuzzy set, it is a type-2 fuzzy set. This concept
can be extended up to type-n fuzzy set.
Definition 1.3 (level-k fuzzy set) the term “level-2 set” indicates fuzzy
sets whose elements are fuzzy sets. The term “level-1 set” is
applicable to fuzzy sets whose elements are no fuzzy sets](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-7-320.jpg)

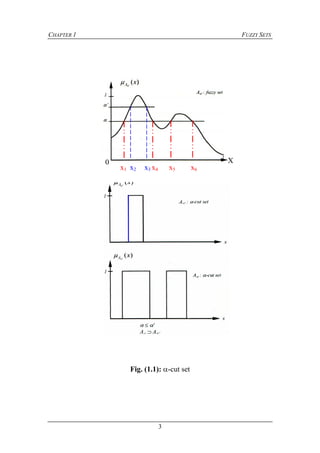
![CHAPTER 1 FUZZY SETS
4
Definition 1.5 (level set) the value α which explicitly shows the value of
the membership function, is in the range of [0, 1]. The
“level set “ is obtained by the α’s. that is,
},0,)({ Xxx
AA
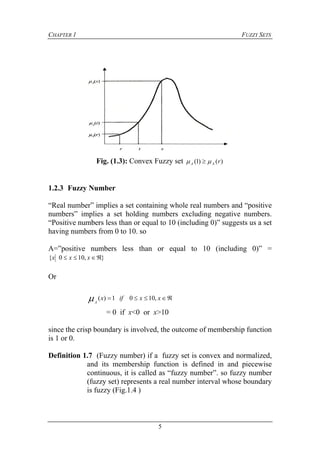
1.2.2 Convex Fuzzy set
Definition 1.6 (convex fuzzy set) assuming universal set X is defined in
n-dimensional Euclidean Vector space
n
. If all the α – cut
sets are convex, the fuzzy set with these α – cut sets is
convex (Fig 1.2 ). In other words, if a relation:
)](),([)( srMint
AAA
where srt )1( ]1,0[,,
n
sr
holds the fuzzy set A is convex.
(Fig. 1.3 ) shows a convex fuzzy set.
Fig. (1.2): Convex Fuzzy set](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-10-320.jpg)

![CHAPTER 1 FUZZY SETS
8
Fig.(1.5): Subset A B
1.3Standard operation of fuzzy set
1.3.1 Fuzzy complement
Complement set A of set A carries the sense of negation. Complement
set may be defined by the following function C,
]1,0[]1,0[: C
Complement function C is designed to map membership function )(x
A
of fuzzy set A to [0,1] and the mapped value is written as ))(( xC
A
. To
be a fuzzy complement function, two axioms should be satisfied.
(Axiom C1) C(0)=1, C(1)=0 (boundary condition)
(Axiom C2) a, b[0,1]
if a<b, then )()( bCaC (monotonic nonincreasing)
symbols a and b stand for membership value of member x in A. for
example, when
)).(())((),()(,,,)(,)( yCxCyxifXyxbyax
AAAAAA
C1 and C2 are fundamental requisites to be a complement function. These
two axioms are called “axiomatic skeleton”. For particular purposes, we
can insert additional requirements,
(Axiom C3) C is a continuous function.](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-14-320.jpg)
![CHAPTER 1 FUZZY SETS
9
(Axiom C4) C is involutive.
C(C(a))= a for all ]1,0[a
The above four axioms hold in standard complement operator
)(1)()(1))(( xxorxxC
AAAA
this standard function is shown in (Fig.1.6 ).
Fig. (1.6): Illustration of standard complement set function.](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-15-320.jpg)
![CHAPTER 1 FUZZY SETS
10
1.3.2 Fuzzy partition
Let A be a crisp set in universal set X and A be a complement set of A.
the condition XAandA
~
result in couple (A, A ) which
decomposes X into two subsets.
Definition 1.9 (Fuzzy partition) in the same manner, consider a fuzzy set
satisfying A
And XA
~
the pair ( A, A ) is defined as fuzzy partition. Usually, if m
subsets are defined in X, m-tuple (A1, A2, … , An )holding the following
conditions is called a fuzzy partition.
1. Ai
i,
2. jiforAA ji
3.
m
i
x
A
Xx
i1
1)(,
1.3.3 Fuzzy union
In general sense, union of A and B is specified by a function of the form,
]1,0[]1,0[]1,0[: U
this union function calculates the membership degree of union BA
from those of A and B.
)](),([)( xxUx
BABA
this union function should obey next axioms.
(Axiom U1) U(0,0)=0, U(0,1)=1, U(1,0)=1, U(1,1)=1
so this union function follows properties of union operation of crisp sets
(boundary condition).
(Axiom U2) U(a,b)=U(b,a) commutativity holds.
(Axiom U3) if a ≤ a' and b ≤ b', U(a,b) ≤ U(a',b') then function U is
a monotonic function.
(Axiom U4) U(U(a,b),c) = U(a,U(b,c)) Associativity holds,
the above four statements are called as “Axiomatic skeleton”. It is often
to restrict the class of fuzzy unions by adding the following axioms.](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-16-320.jpg)
![CHAPTER 1 FUZZY SETS
11
(Axiom U5) function U is continous.
(Axiom U6) U(a,a) = a (idempotency)
1.3.4 Fuzzy intersection
In general sense, intersection BA is defined by the function I.
]1,0[]1,0[]1,0[: I
the argument of this function shows possibility for element x to be
involved in both fuzzy sets A and B.
)](),([)( xxIx
BABA
intersection function holds the following axioms.
(Axiom I1) I(1,1) =1, I(1,0) =0, I(0,1) =0, I(0,0) =0
function I follows the intersection operation of crisp set (boundary
condition).
(Axiom I2) I(a,b) = I(b,a), commutativity holds.
(Axiom I3) if a ≤ a' and b ≤ b', then I(a,b) ≤ I(a',b'), function I is
monotonic function
(Axiom I4) I(I(a,b),c) = I(a,I(b,c)) Associativity holds,
just like in the union function, these four axioms are the “Axiomatic
skeleton”, and the following two axioms can be added.
(Axiom I5) I is a continous function.
(Axiom I6) I(a,a) = a, I is idempotency.](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-17-320.jpg)
![CHAPTER 1 FUZZY SETS
12
1.3.5 Difference in fuzzy set
The difference in crisp set is defined as follows in (Fig.1.7 )
BABA
Fig.(1.7): Difference A - B
In fuzzy set, there are two means of obtaining the difference :
1 Simple difference
Example 1.2 by using standard complement and intersection operations,
the difference operation would be simple. If we reconsider
the previous example, A-B would be ,
)}0,(),1,(),7.0,(),2.0,{( 4321 xxxxA
)}1.0,(),1,(),3.0,(),5.0,{( 4321 xxxxB
)}9.0,(),0,(),7.0,(),5.0,{( 4321 xxxxB
)}.0,(),0,(),7.0,(),2.0,{( 4321 xxxxBABA
2 Bounded difference
Definition 1.10 (Bounded difference) for novice-operator , we define
the membership function as,
)]()(,0[)( xxMaxx
BABA
by this definition, bounded difference of preceding two fuzzy sets is as
follows,
A B= )}0,(),0,(),4.0,(),0,{( 4321 xxxx](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-18-320.jpg)

( 22
Similarly mth
power of fuzzy set Am
may be computed as,
Xxxx m
A
m
A
,)]([)(
this operator is frequently applied when dealing with the linguistic hedge
in expression of fuzzy set.
Definition 1.12 (Cartesian product) Cartesian product applied to multiple
fuzzy sets can be defined as follows,
Denoting )(),......,(),(
21
xxx
nAAA
as membership functions of
AAA n
,......,, 21
.
For AxAxAx nn
...,,, 2211
.
Then, the probability for n-tuple ( xxx n
...,,, 21
) to be involved in fuzzy
set AAA n
......21
is,
)](),...,([),...,,( 121... 121
nAAnAAA
xxMinxxx
nn
.
1.3.8 Disjunctive sum
Disjunctive sum is the name of operation corresponding “exclusive OR”
logic, and it is expressed as the following (fig.1.8)
)()( BABABA ](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-20-320.jpg)
,([)( xxMinx
BABA
)](),(1[)( xxMinx
BABA
)()( BABABA , then
)]}(),(1[)],(1),([{)( xxMinxxMinMaxx
BABABA
(Disjoint sum) the key idea of “Exclusive OR” is elimination of common
area from the union of A and B. with this idea, we can define an operator
for the exclusive OR disjoint sum as follows,
)()()( xxx
BABA
1.4 Fuzzy relation
1.4.1 Definition of fuzzy relation
If a crisp relation R represents that of form sets A to B, for x~ A and y~ B,
its membership function ),( yx
R
is,
Ryxiff
Ryxiff
yx
R
),(0
),(1
),(
This membership function maps BA to set {0,1}.](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-21-320.jpg)
![CHAPTER 1 FUZZY SETS
16
}1,0{: BA
R
We know that the relation R is considered as a set. Recalling the previous
fuzzy concept, we can define ambiguous relation.
Definition 1.14 (Fuzzy relation) Fuzzy relation has degree of
membership whose value lies in [0,1].
]1,0[: BA
R
},,0),()),(),,{(( ByAxyxyxyxR
RR
),( yx
R
is interpreted as strength of relation between x and y. when
),(),,(),( yxyxyx
RR
is more strongly related than ),( yx .
When a fuzzy relation BAR is given, this relation R can be thought
as a fuzzy set in the space BA (Fig.1.9 ) illustrates that the fuzzy
relation R is a fuzzy set of pairs (a, b) of elements where BbAa ii
~
, .](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-22-320.jpg)
![CHAPTER 1 FUZZY SETS
17
Fig.(1.9): Fuzzy relation as a fuzzy set.
Let’s assume a Cartesian product space X1 X2 composed of two sets X1
and X2.This space makes a set of pairs (x1, x2) for all
22
11 ,
Xx
Xx
Given a fuzzy relation R between two sets X1 and X2, this relation is a set
of pairs Rxx ),( 21
. Consequently, this fuzzy relation can be presumed to
be a fuzzy restriction to the set XX 21
. Therefore, XXR 21
.
Fuzzy binary relation can be extended to n-ary relation. If we assume X1,
X2, …, Xn to be fuzzy sets, fuzzy relation XXX n
R 21
can be
said to be a fuzzy set of tuple elements ),,,( 21 xxx n
, where Xx 11
,
Xx 22
, …, Xx nn
.
1.4.2 Operation of fuzzy relation
We know now a relation is one kind of sets. Therefore we can apply
operations of fuzzy set to the relation. We assume BAR and
BAS .
1 Union relation
Union of two relation R and S is defined as follows:
BAyx ),(
)],(),,([),( yxyxMaxyx
SRSR
),(),( yxyx
SR
the symbol is used for Max operation. For n relations, we extend it to
the following,](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-23-320.jpg)
![CHAPTER 1 FUZZY SETS
18
),(),(
321
yxyx
iin RRRRRR
2 Intersection relation
The intersection relation SR of set A and B is defined by the following
membership function,
)],(),,([),( yxyxMinyx
SRSR
),(),( yxyx
SR
the symbol is for the Min operation. In the same manner, the
intersection relation for n-relations is defined by,
),(),(
321
yxyx
iin RRRRRR
3 Complement relation
Complement relation R for fuzzy relation R shall be defined by the
following membership function,
BAyx ),(
),(1),( yxyx
RR
4 Inverse relation
When a fuzzy relation BAR is given, the inverse relation of R-1
is
defined by the following membership function,
BAyx ),(
),(),(
1
yxxy
RR
1.4.3 Composition of fuzzy relation
Definition 1.15 (Composition of fuzzy relation) two fuzzy relations R
and S are defined on sets A, B and C. that is,
CBSBAR , .](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-24-320.jpg)
![CHAPTER 1 FUZZY SETS
19
The composition SRRS of two relations R and S is expressed by the
relation from A to C, and this composition is defined by the following,
For ,),(,),( CBzyBAyx
))],(),,(([),( zyyxMinyx
SR
y
RS Max
)],(),([ zyyx
SR
y
RS from this elaboration is a subset of CA . That is,
.CARS
1.4.4 -cut of fuzzy relation
We have learned about -cut for fuzzy sets, and we know a fuzzy relation
is one kind of fuzzy sets. Therefore, we can apply the -cut to the fuzzy
relation.
Definition 1.16 (-cut relation) we can obtain -cut relation from a
fuzzy relation by taking the pairs which have membership
degrees not less than , assume BAR , and R
is a
-cut relation. Then,
},,),(),{( ByAxyxyx
RR
Note that R
is a crisp relation.
1.5 Extension of fuzzy set
1.5.1 Extension by relation
Definition 1.17 (extension of fuzzy set) let A and B be fuzzy sets and
R denote the relation from A to B. This relation can be
expressed by function f,
ByAx ,
y = f (x) or x = f –1
(y)](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-25-320.jpg)

![CHAPTER 1 FUZZY SETS
21
1.5.3 Extension by fuzzy relation
Definition 1.19 (Extension of fuzzy relation) For a given fuzzy set A,
crisp set B and fuzzy relation BAR , there might be a
mapping function expressing the fuzzy relation R.
membership function of fuzzy set B in B is defined as
follows:
For BBandByAx ,
))],(),(([)(
)(1
yxxMiny
RA
yfx
B Max
.
1.6Characteristics of fuzzy relation
1.6.1 Reflexive relation
For all Ax , if 1),( xx
R
, we call this relation reflexive.
1.6.2 Symmetric relation
When fuzzy relation R is defined on AA , it is called symmetric if it
satisfies the following condition,
AAyx ),(
),(),( xyyx
RR
we say “antisymmetric” for the following case,
yxAAyx ,),(
0),(),(),(),( xyyxorxyyx
RRRR
1.6.3 Transitive relation
Transitive relation is defined as,
AAzxxyyx ,,,,,](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-27-320.jpg)

![CHAPTER 1 FUZZY SETS
23
Definition 1.22 (Strong homomorphism) Given two crisp relations
AAR and BBS , if the function BAh : satisfies
the followings, it’s called “Strong homomorphism” from
(A, R) to (B, S),
For all Axx 21 , ,
SxhxhRxx ))(),((),( 2121
For all Byy 21 , ,
If )(),( 2
1
21
1
1 yhxyhx
Then RxxSyy ),(),( 2121 .
In other words, the inverse image Rxx ),( 21 of Syy ),( 21 always stands
for the homomorphism related by R. here h, we see is a many-to-one
mapping function.
Definition 1.23 (Fuzzy homomorphism) if the relations AAR and
BBS are fuzzy relations, the above morphism is
extended to a fuzzy homomorphism as follows,
For all Axx 21 , and their images Bxhxh )(),( 21 ,
)](),([),( 2121 xhxhxx
SR
.
In other words, the strength of the relation S for ))(),(( 21 xhxh is stronger
than or equal to that of R for ),( 21 xx .
If a homomorphism exists between fuzzy relations (A, R) and (B, S), the
homomorphism h partitions A into subsets nAAA ,,, 21 because it is a
many-to-one mapping.
niAx ji ,,2,1,
Byxh i )( .](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-29-320.jpg)

![CHAPTER 2 FUZZY GROUPS, FUZZY RINGS AND FUZZY FIELDS
25
Chapter (2)
FUZZY GROUPS, FUZZY RINGS AND FUZZY FIELDS
Rosenfield introduced the notion of fuzzy group and showed that many
group theory results can be extended in an elementary manner to develop
the theory of fuzzy group. The underlying logic of the theory of fuzzy
group is to provide a strict fuzzy algebraic structure where level subset of
a fuzzy group of a group G is a subgroup of the group. Reduced fuzzy
subgroup of a group using the general t-norm. However, Rosenfield used
the t-norm ‘min’ in his definition of fuzzy subgroup of a group. The
concepts of fuzzy normal subgroup and fuzzy coset were introduced [6].
2.1 Fuzzy subgroups
Definition 2.1.1: Let G be a group. A fuzzy subset A of a group G is
called a fuzzy subgroup of the group G if
i. μA (xy) = min {μA (x), μA (y)} for every x,y G
and
ii. μA (x –1
) = μA (x) for every x G.
Definition 2.1.2: Let G be a group and e denote the identity element of
the group G. A fuzzy subset A of the group G is called a
fuzzy subgroup of group G if
i. μA (xy –1
) min { μA (x), μA (y)} for every x,y G
and
ii. μA (e) = 1.
Theorem 2.1.1: A fuzzy subset A of a group G is a fuzzy subgroup of the
group G if and only if μA (xy –1
) min { μA (x), μA (y)} for
every x, y G.[87].
Theorem 2.1.2: Let A be a fuzzy subgroup of a group G and x G. Then
μA (xy) = μA (y) for every yG if and only if:
μA (x) = μA (e). [87].](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-31-320.jpg)
![CHAPTER 2 FUZZY GROUPS, FUZZY RINGS AND FUZZY FIELDS
26
2.1.1 Level subset of the Fuzzy subset
Definition 2.1.3: Let A be a fuzzy subset of S. For t [0,1] the set
At ={s S / μA (x) = t} is called a level subset of the
fuzzy subset A.
Theorem 2.1.3: Let G be a group and A be a fuzzy subgroup of G. Then
the level subsets At, for t [0,1], t μA (e) is a
subgroup of G, where e is the identity of G. [87].
Theorem 2.1.4: Let A be a fuzzy subset of a group G. Then A is a fuzzy
subgroup of G if and only if t
AG is a subgroup (called
level subgroup) of the group G for every t [0, μA (e)],
where e is the identity element of the group G. [87].
2.1.2 Improper Fuzzy Subgroup
Definition 2.1.4: A fuzzy subgroup A of a group G is called improper if
μA is constant on the group G, otherwise A is termed as
proper.
2.1.3 Order Of Fuzzy Subgroup
Definition 2.1.5: Let A be a fuzzy subgroup of a group G and H = {x
G / μ (x) = μ (e)} then o (A), (order of A) is defined as
o (A) = o (H).
Theorem 2.1.5: Let A be a fuzzy subgroup of a finite group G then:
o (A) = o(G). [87].
Proof: Let A be a fuzzy subgroup of a finite group with e as its identity
element. Clearly H = {x G |μ (x) = μ(e)}is a subgroup of the
group G for H is a t-level subset of the group G where t = μ(e). By
Lagranges Theorem o(H) = o(G). Hence by the definition of the
order of the fuzzy subgroup of the group G we have o (A)=o (G).](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-32-320.jpg)
![CHAPTER 2 FUZZY GROUPS, FUZZY RINGS AND FUZZY FIELDS
27
2.1.4 Normal Fuzzy Subgroups
The notion of the normal subgroup is one of the central concepts of
classical group theory. It serves a powerful instrument for studying the
general structure of groups. Just as a normal subgroup plays an important
role in the classical group theory, a normal fuzzy subgroup plays a
similar role in the theory of fuzzy subgroup [66].
Definition 2.1.6: Let G be a group. A fuzzy subgroup A of G is called
normal if μA (x) = μA (y –1
x y) for all x,y G.
Definition 2.1.7: We can define a fuzzy subgroup A of a group G to be
fuzzy normal subgroup of a group G if μA (xy) = μA
(yx)for every x,y G. This is just an equivalent
formation of the normal fuzzy subgroup. Let A be a
fuzzy normal subgroup of a group G.
For t [0,1], the set A t = {(x,y) G × G / μA (xy –1
) =
t} is called the t-level relation of A. For the fuzzy
normal subgroup A of G and for t [0,1], A t is a
congruence relation on the group G.
Theorem 2.1.6: Let A be a fuzzy normal subgroup of a group G. Then
for any g G we have μA (gxg –1
) = μA (g –1
xg) for
every x G. [87].
Theorem 2.1.7: A fuzzy subgroup A of a group G is normalized if and
only if μA (e) = 1, where e is the identity element of the
group G. [87].
Proof: If A is normalized then there exists x G such that μA (x) = 1,
but by properties of a fuzzy subgroup A of the group G, μA (x) μA
(e) for every x G. Since μA (x) = 1 and μA (e) μA (x) we have μA
(e) 1. But μA (e) 1. Hence μA (e) = 1. Conversely if μA (e) = 1
then by the definition of normalized fuzzy subset Ais normalized.](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-33-320.jpg)
![CHAPTER 2 FUZZY GROUPS, FUZZY RINGS AND FUZZY FIELDS
28
2.1.5 Fuzzy Subgroups Of a Cyclic Group
Theorem 2.1.8: Let G be a cyclic group of prime order. Then there exists
a fuzzy subgroup A of G such that μA (e) = to and μA (x)
= t1 for all x e in G and to > t1. [87].
Theorem 2.1.9: Let G be a group of prime power order. Then G is cyclic
if and only if there exists a fuzzy subgroup A of G such
that for x, y G,
i. If μA (x) = μA (y) then x= y.
ii. If μA (x) μA (y) then xy.[87].
Theorem 2.1.10: Let G be a group of square free order. Let A be a
normal fuzzy subgroup of G. Then for x,y G,
a. if o(x) / o(y) then μA (y) μA (x).
b. if o(x) =o(y) then μA (y) = μA (x). [87].
Theorem 2.1.11: Suppose that G is a finite group and that G has a
composition chain e = A0 A1…A r = G where
Ai / Ai–1 is cyclic of prime order, i =1, 2, …, r. Then
there exists a composition chain of level subgroups of
some fuzzy subgroup A of G and this composition chain
is equivalent to
e = A0 A1 …A r = G. [87].
2.1.6 Conjugate Fuzzy Subgroups
Definition 2.1.8: let A and B be two fuzzy subgroups of a group G. Then
A and B are said to be conjugate fuzzy subgroups of G
if for some g G, μA (x) = μB (g –1
xg) for every x G.
Theorem 2.1.12: If A and B are conjugate fuzzy subgroups of the group
G then o (A) = o (B). [87].](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-34-320.jpg)
![CHAPTER 2 FUZZY GROUPS, FUZZY RINGS AND FUZZY FIELDS
29
Theorem 2.1.13: Let A and B be any two improper fuzzy subgroups of a
group G. Then A and B are conjugate fuzzy subgroups
of the group G if and only if μA = μB. [87].
Definition 2.1.9: Let A and B be two fuzzy subsets of a group G. We say
that A and B are conjugate fuzzy subsets of the group G
if for some g G we have μA (x) , μB (g –1
xg) for every
x G.
Theorem 2.1.14: Let A and B be two fuzzy subsets of an abelian group
G. Then A and B are conjugate fuzzy subsets of the
group G if and only if μA = μB. [87].
Proof: Let A and B be conjugate fuzzy subsets of group G then for some
g G we have
μA (x) = μB (g –1
xg) for every x G
= μB (g –1
gx) for every x G
= μB (x) for every x G.
Hence μA (x) = μB (x).
Conversely if μA (x) = μB (x) then for the identity element e of
group G, we have μA (x) = μB (e –1
xe) for every x G. Hence A
and B are conjugate fuzzy subsets of the group G.
Theorem 2.1.15: Let A be a fuzzy subgroup of a group G and B be a
fuzzy subset of the group G. If A and B. are conjugate
fuzzy subsets of the group G then B. is a fuzzy subgroup
of the group G. [87].
2.1.7 Fuzzy Coset
Definition 2.1.10: Let A be a fuzzy subgroup of a group G. For any a
G, a A defined by (a μ) x = μA (a –1
x) for every x G
is called the fuzzy coset of the group G determined by
a and μ.
Definition 2.1.11: Let A be a fuzzy subgroup of a group G. For any a
G, a A defined by (a μA) (x) = μA (a –1
x) for every
x G is called a fuzzy coset of A.](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-35-320.jpg)
![CHAPTER 2 FUZZY GROUPS, FUZZY RINGS AND FUZZY FIELDS
30
Example 2.1.1
Let iG ,1 be the group with respect to multiplication.
Define A ׃ G [0, 1] as follows:
iixif
xif
xif
xA
,
4
1
11
1
2
1
The fuzzy cosets i and - i of are calculated as follows:
ixif
ixif
xif
xi A
2
1
1
1,1
4
1
and
ixif
ixif
xif
xi A
2
1
1
1,1
4
1
))((
It is easy to see that these fuzzy cosets iA and - iA are neither
identical nor disjoint.
For (i)(i) (-i)(i) implies i and - i are not identical and (i)(1)
= (-i)(1) implies i and - i are not disjoint.
Definition 2.1.12: Let A be a fuzzy subgroup of a group G. Then for any
a, b G a fuzzy middle coset a A b of the group G is
defined by (a A b) (x) = A (a –1
x b –1
) for every x G.
Example 2.1.2
Consider the infinite group Z = { 0, 1, -1, 2, -2, } with respect to
usual addition. Clearly 2Z is a proper subgroup of Z.](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-36-320.jpg)
![CHAPTER 2 FUZZY GROUPS, FUZZY RINGS AND FUZZY FIELDS
31
Define A ׃ Z [0, 1] by
128.0
29.0
Zxif
Zxif
xA
It's easy to verify that A is a fuzzy subgroup of the group Z. for
any a2Z and b2Z+1 the fuzzy middle coset aAb is given by
129.0
28.0
)(
Zxif
Zxif
xba A
Hence it can be verified that this fuzzy middle coset is not a fuzzy
subgroup of Z.
We have the following theorem
Theorem 2.1.16: If A is a fuzzy subgroup of a group G then for any a
G the fuzzy middle coset a A a –1
of the group G is also
a fuzzy subgroup of the group G. [87].
Theorem 2.1.17:Let A be any fuzzy subgroup of a group G and a A a –1
be a fuzzy middle coset of the group G then
o (a A a –1
) = o(A) for any a G. [87].
Proof: Let A be a fuzzy subgroup of a group G and a G. By Theorem
2.1.12 the fuzzy middle coset a Aa –1
is a fuzzy subgroup of the
group G. Further by the definition of a fuzzy middle coset of the
group G we have (a μA a –1
) (x) = μA (a –1
xa) for every x G.
Hence for any a G, A and a Aa –1
are conjugate fuzzy subgroups
of the group G as there exists a G such that (a μA a –1
) (x) = μA
( a –1
xa) for every x G. By using earlier theorems which states
o(a Aa –1
) = o(A) for any a G.
Example 2.1.3
Let G = S3 the symmetric group of degree 3 and p1,p2,p3 [0,1]
such that p1≥ p2 ≥ p3.](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-37-320.jpg)
![CHAPTER 2 FUZZY GROUPS, FUZZY RINGS AND FUZZY FIELDS
32
Define A ׃ G [0, 1] by
otherwiseifp
xifp
exifp
xA
3
2
1
12
Clearly A is a fuzzy subgroup of a group G and o(A) = number of
elements of the set {x G μA (x) = μA (e) }= number of elements
of the set {e}= 1. Now we can evaluate aAa-1
for every a G as
follows
For a = e we have aAa-1
= A. Hence o(aAa-1
) = o(A) = 1
For a = (12) we have
otherwiseifp
xifp
exifp
xaa A
3
2
1
1
12)(
Hence o(aAa-1
) =1. For the values of a = (13) and (132) we have
aAa-1
to be equal which is given by
otherwiseifp
xifp
exifp
xaa A
3
2
1
1
23)(
Hence o(aAa-1
) =1. for a = (13) and (132). Now for a = (23) and
(123) we have aAa-1
to be equal which is given by
otherwiseifp
xifp
exifp
xaa A
3
2
1
1
13)(
Thus o(aAa-1
) =1. Hence o(aAa-1
) = o(A) = 1 for any a G
From this example we see the functions A and aAa-1
are not equal
for some a G. Thus it's interesting to note that if A is fuzzy](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-38-320.jpg)
![CHAPTER 2 FUZZY GROUPS, FUZZY RINGS AND FUZZY FIELDS
33
subgroup of an abelian group G then the functions A and aAa-1
will
be equal for any a G.
2.1.8 Fuzzy Relation On a Group
Definition 2.1.13: Let R A and R B be any two fuzzy relations on a group
G. Then R A and R B are said to be conjugate fuzzy
relations on a group G if there exists (g1 , g2) G ×
G such that R A (x, y) =R B = (g1
–1
xg1 ,g2
–1
xg2 ) for
every (x,y) G × G.
Definition 2.1.14: Let R A and R B be any two fuzzy relation on a group
G. Then R A and R B are said to be generalized
conjugate fuzzy relations on the group G if there
exists g G such that R A (x,y) = R B (g –1
xg , g –1
yg) for every (x,y) G × G.
Theorem 2.1.18: Let R A and R B be any two fuzzy relations on a group
G. If R A and R B are generalized conjugate fuzzy
relations on the group G then R A and R B are
conjugate fuzzy relations on the group G. [87].
Proof: Let R A and R B be generalized conjugate fuzzy relations on the
group G. Then there exists g G such that R A (x, y) = R B (g –1
xg, g –1
yg) for every (x, y) G × G.
Now choose g1 = g2 = g. Then for (g1, g2) G ×G we have R A
(x,y) = R B (g1
–1
xg1, g2
–1
xg2) for every (x,y) G × G. Thus R A
and R B are conjugate fuzzy relations on the group G.
Theorem 2.1.19: Let Aand B. be conjugate fuzzy subgroups of a group
G. Then
i. A×B. and B×Aare conjugate fuzzy relations on
the group G.](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-39-320.jpg)
![CHAPTER 2 FUZZY GROUPS, FUZZY RINGS AND FUZZY FIELDS
34
ii. A× B. and B× A are generalized conjugate fuzzy
relations on the group G only when at least one of A
or B. is a fuzzy normal subgroup of G. [87].
Theorem 2.1.20: Let R A be a similarity relation on a group G and R B
be a fuzzy relation on the group G. If R A and R B are
generalized conjugate fuzzy relations on the group G
then R B is a similarity relation on the group G. [87].
2.1.9 Fuzzy Symmetric Groups
Definition 2.1.15: Let Sn denotes the symmetric group on {1, 2,… n}.
Then we have the following:
i. Let F (Sn) denote the set of all fuzzy subgroups of
Sn.
ii. Let f F (Sn) then Im f ={ f(x)| x Sn}.
iii. Let f, g F (Sn). If |Im (f)|<|Im (g)| then we write
f < g. By this rule we define max F (Sn).
iv. Let f be a fuzzy subgroup of Sn. If f = max F (Sn)
then we say that f is a fuzzy symmetric subgroup of
Sn.
Theorem 2.1.21: Let f be a fuzzy symmetric subgroup of the symmetric
group S3 then o (Im f) = 3. [87].
Definition 2.1.16: Let G (Sn) = {g / g is a fuzzy subgroup of Sn and g (C
( )) is a constant for every Sn} where C ( )is
the conjugacy class of Sn containing , which denotes
the set of all y Sn such that y = x x –1
for x Sn. If
g = max G(Sn) then we call g as co-fuzzy symmetric
subgroup of Sn.
Theorem 2.1.22:
i. If g is a co-fuzzy symmetric subgroup of the
symmetric group S3 then o (Im (g)) = 3.
ii. If g is a co-fuzzy symmetric subgroup of S4 then,
o (Im (g)) = 4 and](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-40-320.jpg)
![CHAPTER 2 FUZZY GROUPS, FUZZY RINGS AND FUZZY FIELDS
35
iii. If g is a co-fuzzy symmetric subgroup of Sn (n =5)
then o (Im (g)) =3. [87].
Theorem 2.1.23: Every co- fuzzy symmetric subgroup of a symmetric
group Sn is a fuzzy symmetric subgroup of the
symmetric group Sn. [87].
Theorem 2.1.24: Every fuzzy symmetric subgroup of a symmetric group
Sn need not in general to be a co-fuzzy symmetric
subgroup of Sn. [87].
2.1.10 Positive Fuzzy Subgroup
Definition 2.1.17: A fuzzy subgroup A of a group G is said to be a
positive fuzzy subgroup of G if A is a positive fuzzy
subset of the group G.
2.1.11 Pseudo Fuzzy Coset
Definition 2.1.18: Let A be a fuzzy subgroup of a group G and a G,
then the pseudo fuzzy coset (aA)P
is defined by
(a μA)P
(x) = p(a) μA (x) for every x G and for
some p P.
Theorem 2.1.25: Let A be a positive fuzzy subgroup of a group G then
any two pseudo fuzzy cosets of A are either identical
or disjoint. [87].
Theorem 2.1.26: Let A be a fuzzy subgroup of a group G then the
pseudo fuzzy coset (aA)P
is a fuzzy subgroup of the
group G for every a G.
Proof: let A be a fuzzy subgroup of group G. for every x, y in G we have:
(a μA)p
(xy-1
) = p(a) μA (xy-1
)
≥ p(a) min { μA (x), μA (y)}
= min {p(a) μA (x), p(a), μA (y)}
= min {(a μA)p
(x), (a μA)p
(y)}.](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-41-320.jpg)
![CHAPTER 2 FUZZY GROUPS, FUZZY RINGS AND FUZZY FIELDS
36
That is (a μA)p
(xy-1
) ≥ min{(a μA)p
(x), (a μA)p
(y)} for every x, yG.
this proves that (a A)p
is a fuzzy subgroup of the group G.
Example 2.1.4
Let G be the klein four group. Then G = {e, a, b, ab} where a2
= e
= b2
, ab = ba and e is the identity element of G.
Define A ׃ G [0, 1] as follows:
abbxif
exif
axif
xA
,
4
1
1
2
1
Take the +ve fuzzy subset p as follows:
abxif
bxif
axif
exif
xp
4
1
3
1
2
1
1
)(
Now we calculate the pseudo fuzzy cosets of A. For the identity
element e of the group G we have (eA)p
= A .
abbxif
axif
exif
xa
p
A
,
8
1
4
1
2
1
](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-42-320.jpg)
![CHAPTER 2 FUZZY GROUPS, FUZZY RINGS AND FUZZY FIELDS
37
abbxif
axif
exif
xb
p
A
,
12
1
6
1
3
1
and
abbxif
axif
exif
xab
p
A
,
16
1
8
1
4
1
)(
Theorem 2.1.27: Let A be a fuzzy subgroup of a group G and R A : G
G [0 1] be given by R A (x,y) = μA (xy –1
) for every
x,y G. Then
i. R A is a similarity relation on the group G only when
A is normalized
and
ii. A is a pre class of R A and in general the pseudo
fuzzy coset (aA)P
is a pre class of R A for any a G.
[87].
Definition 2.1.19: Let A be a fuzzy subset of a non-empty set X and a
X. We define the pseudo fuzzy coset (aA)P
for some p
P by (a μA)P
(x) = p(a) μA (x) for every x X.
Theorem 2.1.28: Let A and B be any two fuzzy subsets of a set X. Then
for a X (aA)P
(aB )P
if and only if A B . [87].
Definition 2.1.20: Let A be a fuzzy subset of a set X. Then∑ = {B : B is
a fuzzy subset of a set X and B A}is said to be a
fuzzy partition of A if
i.
B
AB and](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-43-320.jpg)
![CHAPTER 2 FUZZY GROUPS, FUZZY RINGS AND FUZZY FIELDS
38
ii. Any two members of are either identical or
disjoint
Theorem 2.1.29: Let A be a positive fuzzy subset of a set X then
i. any two pseudo fuzzy cosets of A are either
identical or disjoint.
ii. Pp
P
AaA
,
iii.
Xa
P
aA
Pp
P
aA
and the equality holds good if
and only if P is normal ,
iv. The collection XaaA
P
is a fuzzy partition of A
if and only if P is normal. [87].
Theorem 2.1.30: Let A be a fuzzy subgroup of a group G and R A : G
G [0,1]be given by R A (x,y) = μA (xy –1
) for every
x,y G. If B is a fuzzy subset of the group G such that
B A then (aB)P
is pre class of R A for any a G .
[87].
Definition 2.1.21: Let A and B be any two fuzzy subsets of a set X and p
P. The pseudo fuzzy double coset (AxB)p
is defined
by (AxB)p
= (x A)P
(x B)P
for x X.
Example 1.2.5
Let X ={1,2,3} be a set. Take B and A to be any two fuzzy subsets
of X given by μA (1) = 0.2, μA (2) = 0.8, μA (3) = 0.4. μB (1) = 0.5,
μB (2) = 0.6 and μB (3) = 0.7 . Then the four +ve fuzzy subset p
such that p(1) = p(2) = p(3) = 0.1, we calculate the pseudo fuzzy
double coset (A x B)p
and this given below.
304.0
206.0
102.0
yif
yif
yif
yBxA
p
Theorem 2.1.31: Let A and B be any two positive fuzzy subsets of a set X
and p P. The set of all pseudo fuzzy double cosets
{(BxA)P
| x X} is a fuzzy partition of (B A ) if and
only if p is normal. [87].](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-44-320.jpg)
![CHAPTER 2 FUZZY GROUPS, FUZZY RINGS AND FUZZY FIELDS
39
Theorem 2.1.32: Let A and B be any two fuzzy subgroups of a group G
and RB A : G G [ 0 ,1 ] be given by R B A (x,y) =
(B A )(xy –1
) for every x,y G. Then
i. R B A is a similarity relation on the group G only
when both B and A are normalized.
ii. (x A)P
is a pre class of R B A for any x G where
p P. [87].
Theorem 2.1.33: Let and B be any two fuzzy subgroups of a group G
and RA B : G G [ 0 ,1 ] be given by
R A B (x,y) = (A B )(xy –1
) for every x,y G.
If B is any fuzzy subset of the group G such that η A
B then η is a pre class of R A B . [87].
Example 2.1.6
Let G = { 1, , 2
}be the group with respect to the usual
multiplication, where denotes the cube root of unity.
Define A, B : G [0,1] by
2
5.0
6.0
10.1
xif
xif
xif
xA
and
2
3.0
4.0
15.0
xif
xif
xif
xB
We found that for every xG. RB A(x,x) = (B A )(xx –1
) =
(B A )(1) = 0.5 .
Hence RB A is not reflexive and hence RB A is not a similarity
relation on the group G.](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-45-320.jpg)
![CHAPTER 2 FUZZY GROUPS, FUZZY RINGS AND FUZZY FIELDS
40
2.1.12 Congruence classes
Definition 2.1.22: Let A be a fuzzy normal subgroup of a group G and At
be a t-level congruence relation of A on G. Let C be a
non-empty subset of the group G. The congruence
class of At containing the element x of the group G is
denoted by [x]A.
The sets )(CAt ={x G [x]A C} and tA (C) = { x G [x]A
C } are called respectively the lower and upper
approximations of the set C with respect to At .
Theorem 2.1.34: Let A be a fuzzy subgroup of a group G. The
congruence class [x]A of At containing the element x of
the group G exists only when A is a fuzzy normal
subgroup of the group G. [87].
2.1.13 Some results of fuzzy normal sub-group
Theorem 2.1.35: Let A be a fuzzy normal subgroup of a group G and t
[0,1]. Then for every x G, [x]A = x t
AG and t
AG is a
normal subgroup of the group G. [87].
Theorem 2.1.36:Let A be a fuzzy normal subgroup of a group G, t
[0,1]and C be a non-empty subsets of the group G.
Then
i. )(CAt = t
AG (C)
ii. )()(ˆ ˆ
CGCA t
At . [87].
Theorem 2.1.37: Let A andB be fuzzy normal subgroups of a group G
and t [0,1]. Let C and D be non-empty subsets of the
group G. Then
i. tA (C) )(ˆ AA t
ii. )(ˆ)(ˆ)(ˆ DACADCA ttt
iii. )()()( DACADCADC ttt
iv. )()( DACADC tt](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-46-320.jpg)
![CHAPTER 2 FUZZY GROUPS, FUZZY RINGS AND FUZZY FIELDS
41
v. )(ˆ)(ˆ DACADC tt
vi. )()()( DACADCA ttt
vii. )(ˆ)(ˆ)(ˆ, DACADCADC ttt
viii. )(ˆ)(ˆˆ CBCABA tttt . [87].
Theorem 2.1.38:Let A be a fuzzy normal subgroup of a group G and t
[0,1]. If C and D are non-empty subsets of the group G
then )(ˆ)(ˆ)(ˆ CDADACA ttt .
Proof: Let A be a fuzzy normal subgroup of a group G and t [0,1]. Let
C and D be any two non-empty subsets of the group G, then
CD ={ab a C and b D}is a non-empty subset of the group G.
We have
)(ˆ CDAt = )(ˆ CDGt
A
= )(ˆ)(ˆ DGCG t
A
t
A
= )(ˆ)(ˆ DGCG tt
Hence )(ˆ)(ˆ)(ˆ CDADACA ttt .
Theorem 2.1.39: Let A be a fuzzy normal subgroup of a group G and t
[0,1]. If C and D are non-empty subsets of the group G
then
).()()( CDADACA ttt
Proof: Let A be a fuzzy normal subgroup of a group G, t [0,1]and C
and D by any two non-empty subsets of the group G. Then CD is
non-empty as C and D are non-empty.
Consider )()()()()()( CDACDGDGCGDACA t
t
A
t
A
t
Att .
Hence ).()()( CDADACA ttt
Theorem 2.1.40: Let A and B be fuzzy normal subgroups of a group G
and t [0, 1]. If A is a non-empty subset of the group
G then
i. )(ˆ)(ˆ)()ˆ( CBCACBA ttt ](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-47-320.jpg)
![CHAPTER 2 FUZZY GROUPS, FUZZY RINGS AND FUZZY FIELDS
42
ii. ).()()()( CBCACBA ttt [87].
Theorem 2.1.41:Let A be a fuzzy normal subgroup of a group G and t
[0,1].If C is a subgroup of the group G then )(ˆ CAt is a
subgroup of the group G.
Proof: Let A be a fuzzy normal subgroup of a group G and t
[0,1].Then t
AG is a normal subgroup of a group G.C is a t
AGˆ rough
subgroup of the group G. By the definition of rough subgroup, we
have t
AGˆ (C) to be a subgroup of the group G. If A is a fuzzy
normal subgroup of a group G, t [0,1]and C will be a non-empty
subset of the group G then tAˆ (C) = t
AGˆ (C) we have tAˆ (C) to be a
subgroup of the group G.
2.1.14 Some results of fuzzy relations
Definition 2.1.23: Let A be a fuzzy relation on S and let B be a fuzzy
subset of S. Then A is called a fuzzy relation on B if
μA (x, y) min (μB (x), μB (y)) for all x, y S.
For any two fuzzy subsets B and A of S; the cartesian product of A
and C is defined by(μA μB)(x, y)=min (μA (x), μB (y)) for all x, y
S.
Let B be a fuzzy subset of S. Then the strongest fuzzy relation on B
is AB defined by AB (x, y) = (μB μB )(x, y) = min (μB (x), μB (y)) for
all x, y S.
Theorem 2.1.42:Let A and B be fuzzy subsets of S. Then
i. A B is a fuzzy relation on S.
ii. (A B )t =A t B t for all t [0, 1]. [87].
2.1.15 Linearly independent fuzzy singletons
Definition 2.1.24: A system of fuzzy singletons ktkt xx )(,....,)( 11 where 0 <
ti < μA (xi) for i =1, 2, …, k is said to be linearly](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-48-320.jpg)
![CHAPTER 2 FUZZY GROUPS, FUZZY RINGS AND FUZZY FIELDS
43
independent in A if and only if
ttkkt k
xnxn 0)(....)( 111 implies n1x1 = ... =nk xk =0,
where ni Z, i =1,2,…,k and t [0,1]. A system of
fuzzy singletons is called dependent if it is not
independent.
An arbitrary system of fuzzy singleton is independent in A if and
only if every finite sub-system of is independent.
We let denote a system of fuzzy singletons such that for all xt ,
0 < t μA (x). *={x xt } and t = At * for all,
t [0, A(0)].
Theorem 2.1.43: is independent in A if and only if the fuzzy subgroup
of G generated by in A is a fuzzy direct sum of fuzzy
subgroup of G whose support is cycle i.e. for
Iixtx iAiti i
),(0)( holds = .)( iti
Ii
x
[87].
2.2 Fuzzy Rings
In 1982 LIU, W-J., defined and studied fuzzy subrings as well as
fuzzy ideals. Subsequently among ZHANG, Yue fuzzified certain
standard concepts on rings and ideals.
2.2.1 Fuzzy subrings and Fuzzy ideals
Definition 2.2.1: Let A be any fuzzy subset of a set S and let t [0,1].
The set {s S | μA (x) t} is called a level subset of A
and is symbolized by At. Clearly At As whenever
t > s.
Definition 2.2.2: Let ‘ ’ be a binary composition in a set S and µ, σ be
any two fuzzy subsets of S. The product µσ of µ and σ is
defined as follows:](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-49-320.jpg)
![CHAPTER 2 FUZZY GROUPS, FUZZY RINGS AND FUZZY FIELDS
44
(μA μB)(x) =
.,exp0
,minsup
Szyallforzyasressiblenotisif
Szywherezy BA
zyx
Definition2.2.3:A fuzzy subset A of a ring R is called a fuzzy subring of R
if for all x, y R the following requirements are met
i. μA (x – y) min (μA (x), μA (y))and
ii. μA (xy) min (μA (x), μA (y))
Now if the condition (ii)is replaced by μA (xy) max (μA (x), μB
(y)) then A will be called a fuzzy ideal of R.
Theorem 2.2.1: Let A be any fuzzy subring / fuzzy ideal of a ring R. If,
for some x, y R, μA (x) < μB (y), then μA (x – y) = μA (x) =
μA (y – x). [87].
Definition 2.2.4: Let A be any fuzzy subring / fuzzy ideal of a ring R and
let 0 t μA (0). The subring / ideal At is called a
level subring / level ideal of A.
Theorem 2.2.2: A fuzzy subset A of a ring R is a fuzzy ideal of R if and
only if the level subsets At , t Im(A) are ideals of R.
[87].
Theorem 2.2.3: If A is any fuzzy ideal of a ring R, then two level ideals
1tA and 2tA (with t1 < t2) are equal if and only if there is
no x in R such that t1 μA (x) t2. [87].
Theorem 2.2.4: The level ideals of a fuzzy ideal A form a chain. That is if
Im A = {t0 , t1 ,… , tn } with t0 > … > tn , then the chain
of level ideals of A will be given by
......10
RAAA nttt [87].
Theorem 2.2.5: The intersection of any family of fuzzy subrings (fuzzy
ideals) of a ring R is again a fuzzy subring (fuzzy ideal)
of R. [87].](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-50-320.jpg)
![CHAPTER 2 FUZZY GROUPS, FUZZY RINGS AND FUZZY FIELDS
45
Theorem 2.2.6: Let A be any fuzzy subring and be any fuzzy ideal of a
ring R. Then A is a fuzzy ideal of the subring {x
R / μA (x) = μA (0)}. [87].
Theorem 2.2.7: Let I0 I1 In = R be any chain of ideal of a ring
R. Let t0 , t1 , … , tn be some numbers lying in the
interval [0,1] such that t0 > t1 > … > tn. Then the fuzzy
subset A of R defined by
niIIxift
Ixift
x
iii
o
A
,....,2, 1
0
is a fuzzy ideal of R with FA = {Ii I =0, 1, 2, …, n. [87].
Definition 2.2.5: Let A and θ be any fuzzy ideals of a ring R. The product
A o θ of A and θ are defined by
,,minminsup iiA
zyx
zyxA
i
ii
where x, yi zi R.
Notation: At times we also will make use of this notation. Let A (μ) be
any subset (fuzzy subset) of a ring R. The ideal (fuzzy subring
/fuzzy ideal) generated by A (μ) is denoted by A (μ).
Theorem 2.2.8: Let A be a fuzzy subset of a ring R with card Im A <8.
Define subrings Ri of R by
zxRxR A
Rz
A sup0
and
kizxRxRR A
RRz
Aii
i
1,sup
1
1
where k is such that Rk = R. Then k < card Im A. Also the fuzzy
subset A* of R is defined by](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-51-320.jpg)
![CHAPTER 2 FUZZY GROUPS, FUZZY RINGS AND FUZZY FIELDS
46
kiRRxifz
Rxifz
x
iiA
RRz
A
Rz
A
i
1, 1
0
sup
sup
1
is a fuzzy subring generated by A in R. [87].
Definition 2.2.6: If A is any fuzzy ideal of a ring R, then the fuzzy ideal
A' of R A defined by A'(Ax*) = μA(x) for all x R is
called the fuzzy quotient ideal determined by A.
Theorem 2.2.9: If A is any fuzzy ideal of a ring R, then the map f : R
RA defined by f(x) = Ax* for all x R is a
homomorphism with kernel A t , where t = μA (0). [87].
Theorem 2.2.10: If A is any fuzzy ideal of a ring R, then each fuzzy ideal
of R A corresponds in a natural way to a fuzzy ideal of R.
Proof: Let A' be any fuzzy ideal of R A. It is entirely straightforward
matter to show that the fuzzy subset θ of R defined by θ (x) = A'
(Ax*) for all x R, is a fuzzy ideal of R.
2.2.2 Fuzzy prime ideal
Definition 2.2.7: A non-constant fuzzy ideal A of a ring R is called fuzzy
prime if for any fuzzy ideals A1 and A2 of R the
condition A1 A2 A implies that either A1 A or A2
A.
Theorem 2.2.11: The level ideal At , where t = μA (0) is a prime ideal of
the ring R. [87].
Definition 2.2.8: A fuzzy ideal A of a ring R, not necessarily non-
constant is called fuzzy prime if for any fuzzy ideals A1
and A2 of R the condition A1 A2 A implies that either
A1 A or A2 A.](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-52-320.jpg)
![CHAPTER 2 FUZZY GROUPS, FUZZY RINGS AND FUZZY FIELDS
47
Theorem 2.2.12: Any constant fuzzy ideal A of a ring R is fuzzy prime.
[87].
Theorem 2.2.13: If A is any non-constant fuzzy ideal of a ring R, then A
is fuzzy prime if and only if l Im A: the ideal At , t =
μA (0) is prime and the chain of level ideals of A
consists of At R. [87].
2.2.3 Irreducible fuzzy ideals
Definition 2.2.9: An ideal I of a ring R will be said to be irreducible if I
cannot be expressed as I1 I2 where I1 and I2 are any
two ideals of R properly containing I, otherwise I is
termed reducible.
Theorem 2.2.14: Any prime ideal of ring R is irreducible. [87].
Theorem 2.2.15: In a commutative ring with unity, any ideal, which is
both semiprime and irreducible, is prime. [87].
Theorem 2.2.16: Every ideal in a Noetherian ring is a finite intersection
of irreducible ideals. [87].
Theorem 2.2.17: Every irreducible ideal in a Noetherian ring is
primary. [87].
Definition 2.2.10: A fuzzy ideal A of a ring R is called fuzzy irreducible if
it is not a finite intersection of two fuzzy ideals of R
properly containing A, otherwise A is termed fuzzy
reducible.
Theorem 2.2.18: If A is any fuzzy prime ideal of a ring R, then A is fuzzy
irreducible. [87].
Theorem 2.2.19: If A is any non-constant fuzzy irreducible ideal of a
ring R, then the following are true.
i. 1 Im A .
ii. There exists α [0,1] such that μA (x) = α for all
x R {x R / μA (x) = 1}.
iii. The ideal {x R / μA (x) = 1} is irreducible. [87].](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-53-320.jpg)
![CHAPTER 2 FUZZY GROUPS, FUZZY RINGS AND FUZZY FIELDS
48
2.2.4 Fuzzy coset of fuzzy ideal
Theorem 2.2.20:
i. Let A be any fuzzy ideal of a ring R and let
t = μA (0). Then the fuzzy subset A* of R/ At defined
by
A (x + At) = μA (x) for all x R, is a fuzzy ideal
of R/ At .
ii. If B is an ideal of R and θ is a fuzzy ideal of R/A such
that
θ (x + B) = θ(B) only when x B, then there exists a
fuzzy ideal B of R such that At = B where t = μA (0)
and θ = A*.[87].
Definition 2.2.11: Let A be any fuzzy ideal of a ring R and let x R. The
fuzzy subset Ax* of R defined by Ax*(r) = μA (r –x) for
all r R is termed as the fuzzy coset determined by x
and A.
Theorem 2.2.21: Let A be any fuzzy ideal of a ring R. Then R A , the set
of all fuzzy cosets of A in R is a ring under the binary
compositions.
Ax* + Ay* = A*x+y and
Ax* Ay* = A*xy for all x,y R. [87].
2.2.5 Fuzzy semiprime ideal
Definition 2.2.12: A fuzzy ideal A of a ring R is called fuzzy semiprime if
for any fuzzy ideal θ of R, the condition θ m
A (m
Z +
) implies θ A.
Theorem 2.2.22: Let A be any fuzzy subset of a ring R. Then μA (x) = t if
and only if x A t and x As for all s > t. [87].
Theorem 2.2.23: A fuzzy ideal A of a ring R is fuzzy semiprime if and
only if A, t Im A, is a semiprime ideal of R. [87].](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-54-320.jpg)
![CHAPTER 2 FUZZY GROUPS, FUZZY RINGS AND FUZZY FIELDS
49
Theorem 2.2.24: An ideal A of a ring R is semiprime if and only if ψA is
a fuzzy semiprime ideal of R. [87].
Theorem 2.2.25: If A is any fuzzy semiprime ideal of a ring R, then RA,
the ring of fuzzy cosets of A in R is free from non-zero
nilpotent elements. [87].
Theorem 2.2.26: Let A be any fuzzy ideal of a ring R such that Im A =
{t, s} with t > s. If the ring R A has no non-zero nilpotent
elements, then the fuzzy ideal A is fuzzy semiprime.
[87].
Theorem 2.2.27: A ring R is regular if and only if every fuzzy ideal of R
is idempotent. [87].
Theorem 2.2.28: A ring R is regular if and only if every fuzzy ideal of R
is fuzzy semiprime. [87].
2.2.6 L-Fuzzy ideals
We replace the interval [0, 1] by a finite lattice L which has 0 to be
the least element and 1 to be the largest element. All the while, fuzzy
ideals have been defined over [0, 1] when we define it over a lattice L we
call them L-fuzzy ideal [91].
Definition 2.2.13: An L-fuzzy ideal is a function J : R L (R is a
commutative ring with identity L stands for a lattice
with 0 and 1) satisfying the following axioms
i. J (x + y) J (x) J(y).
ii. J (–x) = J(x).
iii. J (xy) J(x) J(y).
Theorem 2.2.29:
i. A function J : R L is a fuzzy ideal if and only if
J (x – y) J (x) J(y) and
J (xy) J(x) J(y).](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-55-320.jpg)
![CHAPTER 2 FUZZY GROUPS, FUZZY RINGS AND FUZZY FIELDS
50
ii. If J: R L is a fuzzy ideal then
a- J (0) J(x) J(1) for all x R.
b- J (x-y) = J (0) implies J(x) = J(y)
for all x, y R
c- The level cuts J α =x R J(x) α
are ideals of R.
Conversely if each J a is an ideal
then J is a fuzzy ideal. [87].
Theorem 2.2.30: If f : R R' is an epimorphism of rings, then there is
one to one correspondence between the ideals of R' and
those of R which are constant on ker f. If J is a fuzzy
ideal of R which is constant on ker f, then f (J) is the
corresponding fuzzy ideal of R'. If J' is a fuzzy ideal of
R', then,
f –1
(J') is the corresponding fuzzy ideal of R. [87].
2.2.7 L-Prime fuzzy ideals
By a prime fuzzy ideal we mean a non-constant fuzzy ideal
P : R L satisfying the following condition of primeness
P (xy) = P(x) or
P (xy) = P(y) for all x, y R.
Theorem 2.2.31: If P: R L is a prime fuzzy ideal, then the set P(R) of
membership values of P is a totally ordered set with the
least element P(1) and the greatest element P(0). [87].
Theorem 2.2.32: A fuzzy ideal P: R L is prime if and only if every
level cut Pα = {x R | P(x) α } is prime for all a >
P(1) For a = P(1), Pα = R. [87].
Theorem 2.2.33: Let Z be a non-empty subset of R. Z is a prime ideal of
R if and only if χz: R L is a prime fuzzy ideal. [87].
Theorem 2.2.34: Let R be a principal ideal domain (PID). If P : R L
is a prime fuzzy ideal and PP (0) ≠ 0, then P (R) has two
elements. P is properly fuzzy if and only if P(R) has
three elements. We see a properly fuzzy prime ideal of a](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-56-320.jpg)
![CHAPTER 2 FUZZY GROUPS, FUZZY RINGS AND FUZZY FIELDS
51
PID R is equivalent to the fuzzy ideal P : R L of the
following type:
P(0) = 1,
P (x) = α
for all x P1 {0}. P(x) = 0 for all x R P1 where P1 is a prime
ideal of R and 0 < α < 1. [87].
Definition 2.2.14: A finite strictly increasing sequence of prime ideals of
a ring R, P0 P1 P2 … Pn is called a chain of
prime ideals of length n. The supremum of the lengths
of all chains is called the dimension of R .
Definition 2.2.15: Let R be a ring. Then { |P(R)| ∕P:R [0, 1] is a
prime fuzzy ideal} is called the fuzzy dimension of R.
Theorem 2.2.35:
i. The dimension of R is n (< ) if and only if its fuzzy
dimension is n + 2.
ii. An artinian ring has no properly fuzzy prime ideal.
iii. A Boolean ring has no properly fuzzy prime ideal. [87].
Theorem 2.2.36:
i. Let f : R R' is an epimorphism of rings. If P: R L
is a prime fuzzy ideal which is constant on ker f then,
f (P) : R' L is a prime fuzzy ideal.
ii. If f : R R' is a homomorphism of rings. If P' : R' L
is a fuzzy prime ideal then f –1
(P') is a prime fuzzy ideal
of R.
iii. Let f : R R' be an epimorphism of ring.
(a) Let P : R L be a fuzzy ideal which is constant on
ker f. Then P is prime if and only if f(P) : R' L is
prime.
(b) Let P' : R' L be a fuzzy ideal. Then P' is prime if
and only if f –1
(P') : R L is prime. [87].](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-57-320.jpg)
![CHAPTER 2 FUZZY GROUPS, FUZZY RINGS AND FUZZY FIELDS
52
2.2.8 L-Primary fuzzy ideals
Definition 2.2.16: A fuzzy ideal Q : R L is called primary if Q(xy) =
Q(0) implies Q(x) = Q(0) or Q(y n
) = Q(0) for some
integer n > 0.
Definition 2.2.17: A fuzzy ideal Q : R L is called primary, if either Q
is the characteristic function of R or
i. Q is non-constant.
ii. A o B Q A Q or B Q is the intersection of
all prime fuzzy ideals.
Definition 2.2.18: A fuzzy ideal Q : R L is called primary, if
i. Q is non-constant and
ii. for all x,y R and r, s L if x,y Q then xr Q or
yn
s Q for some positive integer n.
Theorem 2.2.37:
i. Let Q be an ideal of R. The characteristic function χ Q is
a primary fuzzy ideal if and only if Q is a primary ideal.
ii. If Q : R L is primary then its level cuts Q α = {x R
∕Q(x) α}, α L, are primary.
iii. Every prime fuzzy ideal is primary. [87].
Theorem 2.2.38:
i. Let f : R R' be an epimorphism of
rings. If Q : R L is a primary fuzzy
ideal of R which is constant on ker f, then f(Q) is a
primary fuzzy ideal of R'.
ii. Let f : R R' be a homomorphism of rings. If Q' : R'
L is a primary fuzzy ideal of R' then f –1
(Q') is a
primary fuzzy ideal of R .](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-58-320.jpg)
![CHAPTER 2 FUZZY GROUPS, FUZZY RINGS AND FUZZY FIELDS
53
iii. Let f : R R' be an epimorphism of rings and Q : R
L and
Q':R' L be a fuzzy ideals.
a) Q' is primary if and only if f –1
(Q') is
primary.
b) If Q is constant on ker f, then Q is primary if
and only if f (Q) is primary. [87].
2.2.9 L-weak primary fuzzy ideals
Definition 2.2.19: A fuzzy ideal J : R L is said to be weak primary or
in short w-primary if J(xy) = J(x) or J(xy) J(y n
) for
some integer n > 0.
Theorem 2.2.39: Every primary fuzzy ideal is w-primary. In particular,
every prime fuzzy ideal is w-primary. [87].
Theorem 2.2.40: A fuzzy ideal is w-primary if and only if each of its level
cuts is primary. [87].
Theorem 2.2.41: Let Q be an ideal of R. The characteristic function χ Q
is w-primary if and only if Q is primary. [87].
Theorem 2.2.42: Let f : R R' be a homomorphism of rings, and Q : R
L and Q' : R' L be fuzzy ideals.
i. If f is w-primary then so is f –1
(Q').
ii. Let f be an epimorphism. Then Q is w-primary if and
only if f(Q) is w primary.
iii. Let f be an epimorphism then Q' is w-primary if
and only if f –1
(Q) is w-primary. [87].
2.2.10 Fuzzy nil-radical
Let I be an ideal of R, nil-radical defined as
I = {x R xn
I ,n > 0 }.](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-59-320.jpg)
![CHAPTER 2 FUZZY GROUPS, FUZZY RINGS AND FUZZY FIELDS
54
Definition 2.2.20: If J : R L is a fuzzy ideal, then the fuzzy set J : R
L defined as J (x)= { J (xn
) n > 0 } is
called the fuzzy nil radical of J.
Theorem 2.2.43:
i. If J : R L is a fuzzy ideal, then J is a fuzzy ideal.
ii. If I is an ideal of R, then 1X = χ I
.
iii. For any 0 1 and a fuzzy ideal J : R L,( J )
where L is a totally ordered set, J = (x R J(x) > )
and ( J ) ={x R / )(xJ }.
iv. In case of non-strict level cuts J ( J ) . [87].
Theorem 2.2.44:
i. If f : R R' is an epimorphism of rings and J : R L is
a fuzzy ideal, then f ( J ) )(Jf . Further if J is
constant on ker f then f ( J ) = )(Jf .
ii. If f : R R' is a homomorphism of rings and J' : R' L is
a fuzzy ideal then f -1
( 'J ) = )'(1
Jf
.[87].
Theorem 2.2.45: If J : R L and K : R L are fuzzy ideals, then the
following hold:
i. J = J .
ii. If J K, then J K .
iii. KJ = J K .
iv. If J : R L is a fuzzy ideal with supremum
property then J = ( J ) .
v. If P : R L is prime then p = P.
vi. If Q : R L is a primary fuzzy ideal with
supremum property then Q is the smallest prime
fuzzy ideal containing Q.
vii. If L is a totally ordered set and Q : R L is a
primary fuzzy ideal, then Q is the smallest prime](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-60-320.jpg)
![CHAPTER 2 FUZZY GROUPS, FUZZY RINGS AND FUZZY FIELDS
55
fuzzy ideal containing Q. [87].
Definition 2.2.21: Let J :R L be a fuzzy ideal and P : R L denote a
prime fuzzy ideal containing J. The fuzzy ideal r (J) =
{P | J P} is called the prime fuzzy radical of J.
Theorems 2.2.46:
i. If J : R L is a fuzzy ideal, then J r(J).
ii. If L is a totally ordered set and J : R L is a fuzzy ideal
then J r(J). [87].
Definition 2.2.22: A fuzzy ideal S : R L is called semiprime fuzzy
ideal if S(x 2
) = S(x) for all x R.
Theorem 2.2.47:
i. Let S : R ( L be a fuzzy ideal, S is semiprime if and
only if its level cuts, Sα = (x ( R| S(x) ( α) are
semiprime ideals of R, for all α L.
ii. Let S be an ideal of R . S is semiprime if and only if
its characteristic function χS is a semiprime fuzzy
ideal of R.
iii. Let f : R R' be a homomorphism. If S' : R'. L is a
semiprime fuzzy ideal of R then f –1(S') is a
semiprime fuzzy ideal of R.
iv. Let f : R R' be an epimorphism and S : R L
be a semiprime fuzzy ideal of R which is constant on
ker f.
Then f(S) is a semiprime fuzzy ideal of R'. Thus by
the correspondence theorem between semiprime
fuzzy ideals of R' and those of R which are constant
on the kernel of f.
v. Every prime fuzzy ideal is semiprime fuzzy ideal.
vi. Intersection of semiprime fuzzy ideal is a
semiprime fuzzy ideal. In particular intersection of
prime fuzzy ideals is a semiprime fuzzy ideal.
vii. If S : R L is a semiprime fuzzy ideal, then the
quotient ring R/S is prime. [87].](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-61-320.jpg)
![CHAPTER 2 FUZZY GROUPS, FUZZY RINGS AND FUZZY FIELDS
56
Theorem 2.2.48: If S : R L is a fuzzy ideal then the following are equivalent
i. S is semiprime.
ii. Each level cut of S is semiprime.
iii. S(x n
) = x for all integers n > 0 and x R.
iv. J 2
S implies J S for all fuzzy ideals J : R L.
v. J n
S for n > 0 implies J S for all fuzzy ideals
J : R L.
vi. S = s where s is the fuzzy nil radical of S when L
is totally ordered and each of the above statements is
equivalent to the following:
a. S coincides with its prime fuzzy radical.
b. S = {P / P C} where C is a class of
prime fuzzy ideals. [87].
2.2.11 Extension of fuzzy subrings and fuzzy ideals
Let R be a subring of S. If I is an ideal of R, we let I e
denote the
ideal of S extended by I.
Theorem 2.2.49:Let R be a subring of S and let A be a fuzzy ideal of R
such that A has the sup property. If
)Im(
)(
At
e
t SA
and for all s, t Im (A),s t, At (As)e
=As, then A has a unique
extension to a fuzzy ideal A e
of S such that (A e
)t =(At )e
for all t
Im (A) and Im(A e
)=Im(A). Let R be a commutative ring with
identity. Let M be a multiplicative system in R. Let N ={x R | mx
=0 for some m M}.Then N is an ideal of R. Unless otherwise
specified, we assume N =0 i.e. M is regular. Let RM denote the
quotient ring of R with respect to M. Since N =0,we can assume
that R RM. If A is a fuzzy subring of R, we assume A(1)=A(0).
[87].
Theorem 2.2.50:Let A be a fuzzy subring of R such that A has the sup
property. Then A can be extended to a fuzzy subring A e](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-62-320.jpg)
![CHAPTER 2 FUZZY GROUPS, FUZZY RINGS AND FUZZY FIELDS
57
of RM such that for all x, y R, y a unit. A e
(xy –1
)
min {A e
(x), A e
(y)} if and only if for all s, t Im (A) ,
s t, At (At )M =As where Ms =M As for all,
s Im (A). If either condition holds, A e
can be chosen
so that (Ae
)t = (At)M for all t Im (A) and
Im (A e
)=Im(A). [87].
Theorem 2.2.51:Let A be a fuzzy subring of R such that A has the sup
property. Then A can be extended to a fuzzy quasi local
subring A e of RP for all s, t Im (A), s t, At
(As )P =As where Ps =P .As for all s Im (A). [87].
Theorem 2.2.52:Let R be an integral domain and let Q denote the
quotient field of R. Let A be a fuzzy subring of R such
that A has the sup property. Let Qt denote the smallest
subfield of Q which contains At, for all t Im (A).Then
A can be extended to a fuzzy subfield of Q if and only if
for all s, t Im (A),s t, At Qs =As . [87].
2.2.12 Extension of fuzzy prime ideals.
Let R and S be rings and let f be a homomorphism of R into S. Let
T denote f (R).If I is an ideal in R, then the ideal (f(I))e
(or simple I e
)
will be defined to be the ideal of S generated by f (I)and is called the
extended ideal or extension of I. If J is an ideal of S, the ideal J c
=f –1
(J)
is called the contracted ideal or the contraction of J [38].
Definition 2.2.23:Let A and B be fuzzy subsets of R and T respectively.
Define the fuzzy subsets f(A)of T and f –1
(B)of R by
f(A) (y)=sup { μA (x) f(x) = y}
for all y T, f –1
(B) (x) = B (f(x)) for all x R .
Theorem 2.2.53:Suppose A and B are fuzzy ideals of R and T
respectively. Then
i. f (A) and f –1
(B) are fuzzy ideals of T and R
respectively.
ii. f (A) (0)=μA(0).
iii. f –1 (B) (0)= μB (0). [87].](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-63-320.jpg)
![CHAPTER 2 FUZZY GROUPS, FUZZY RINGS AND FUZZY FIELDS
58
Theorem 2.2.54:Let A be a fuzzy ideal of R. Then
i. f(A) (f(A))
ii. if A has the sup property then f (A)) =f(A ).[87].
2.2.13 f-invariant
Definition 2.2.24:Let A be a fuzzy ideal of R. A is called f-invariant if
and only if for all x, y R, f(x)=f(y)implies,
μA (x)= μA (y). [87].
Theorem 2.2.55:Let A be a fuzzy ideal of R. Then A is a fuzzy prime ideal
of R if and only if μA (0)=1,Im(A) = 2 and A is a
prime ideal of R. [87].
Theorem 2.2.56:Let A be an f-invariant fuzzy ideal of R such that A has
the sup property. If A is a prime ideal of R, then f (A)
is a prime ideal of T. [87].
Theorem 2.2.57:Let A be an f-invariant fuzzy ideal of R such that Im(A)
is finite. If A is a prime ideal of R then f (A)=(f(A)) .
[87].
Theorem 2.2.58:Let A be an f-invariant fuzzy ideal of R. If A is a fuzzy
prime ideal of R then f(A)is a fuzzy prime ideal of T.
[87].
2.3 Fuzzy Fields
Definition 2.3.1: Let F be a field, A fuzzy subfield of F is a function A
from F into the closed interval [0, 1] such that for all
x, y F
(μA (x –y) min { μA (x), μA (y)} and
μA (xy –1
) min { μA (x), μA (y)}; y 0.
Let A be a fuzzy subset of F and let A ={xF / μA (x) μA (1)}
where 1 denotes the multiplicative identity of F. Let K be a subfield
of F and let S (F/K) denotes the set of all fuzzy subfields, A of F](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-64-320.jpg)
![CHAPTER 2 FUZZY GROUPS, FUZZY RINGS AND FUZZY FIELDS
59
such that K A. Here we just recall certain properties of field
extensions F/K in terms of fuzzy subfields and conversely.
Let A be a fuzzy subset of the field F. For 0 t 1, let At ={x F /
μA (x) t}.Then A=At when t = μA (1).
Theorem 2.3.1:
i. If A is a fuzzy subset of F and s, t Im (A), the image of
A, then s t if and only if As At and s =t if and only if
As =At.
ii. If A is a fuzzy subfield of F ,then for all x F, x 0,
μA (0) μA (1) μA (x)= μA (–x)= μA (x –1
). [87].
Theorem 2.3.2: Let A be a fuzzy subset of F. If At is a subfield of F for all
t Im (A), then A is a fuzzy subfield of F. Conversely, if A
is a fuzzy subfield of F, then for all t such that 0 t A
(1), At is a subfield of F. [87].
Theorem 2.3.3: Let S be a subset of F such that S (Cardinality of S)
2.Then S is a subfield of F if and only if S, the
characteristic function of S, is a fuzzy subfield of F.
Recall if K be a subfield of F i.e. F is an extension field of
K then the field extension is denoted by F/K.
S(F/K)denotes the set of all fuzzy subfields A of F such
that A K and A is a subfield of F. [87].
Theorem 2.3.4: Let F1 F2 Fi be a strictly ascending chain of
subfields of F such that Fi =F. Define the fuzzy subset
A of F by μA (x)=ti, if x Fi Fi–1 where ti > ti+1
for i =1,2, and Fo = .Then A is a fuzzy subfield of F.
Proof: Let x, y F. Then x –y Fi Fi –1 for some i. Hence either
x Fi –1 or y Fi –1.Thus A(x –y) = ti min { μA (x), μA (y)},
similarly μA (xy –1
) =min { μA (x), μA (y)} for y 0.](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-65-320.jpg)
![CHAPTER 2 FUZZY GROUPS, FUZZY RINGS AND FUZZY FIELDS
60
Theorem 2.3.5: Let F = F0 F1 Fi be a strictly descending
chain of subfields of F. Define the fuzzy subset A of F by
μA (x) = ti –1 if x Fi –1 Fi where ti –1 < ti <1 for i =1,2,
and μA (x) =1 if x Fi. Then A is a fuzzy subfield
of F. [87].
Theorem 2.3.6: Let F /K be a field extension and let B be a fuzzy subfield
of K. Let r =inf { μB (x) / x K}.Define the fuzzy subset A
of F by μA (x) = μB (x) for all x K and μA (x) = m for all
x F K where 0 m r. Then A is a fuzzy subfield of
F. [87].
Theorem 2.3.7: If F is a finite field, then every fuzzy subfield of F is finite
valued. [87].
Theorem 2.3.8: Let F/K be a field extension. Then [F: K] < if and only
if every A S, (F/K) is finite valued. [87].
Theorem 2.3.9:
i. Suppose that F has characteristic p >0.Then F is finite if
and only if every fuzzy subfield A of F is finite-valued.
ii. Suppose that F has characteristic 0.
Then [F: Q] < if and only if every fuzzy subfield A of F is finite
valued. [87].
Theorem 2.3.10: Suppose that F/K is finitely generated. Then F/K is
algebraic if and only if every A S (F/K) is finite
valued. [87].
Theorem 2.3.11:F/K has no proper intermediate fields if and only if
every A S (F/K) is three valued or less. [87].
Theorem 2.3.12: The following conditions are equivalent.
i. The intermediate fields of F/K are chained.
ii. There exists C S (F/K) such that for all A S (F/K). LA
LC.](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-66-320.jpg)
![CHAPTER 2 FUZZY GROUPS, FUZZY RINGS AND FUZZY FIELDS
61
iii. For all A,B S (F/K) and for all At LA and Bs LB
either At Bs or Bs At.
We give a necessary and sufficient condition for F/K to be simple.
[87].
Theorem 2.3.13:F/K is simple if and only if there exists c F such that
for all AS (F/K) and for all x F, μC (c) μA (x). [87].
Theorem 2.3.14: Suppose that [F: K] <. Then the following conditions
are equivalent.
i. F/K has a finite number of intermediate fields.
ii. There exists C1, C2,…,Cn S(F/K) such that for all
A S(F/K). LA LC1 LCn.
iii. There exists c F such that for all A S (F/K)and for
all x F, μC (c) μA (x).
Theorem 2.3.15: Let F/K be a field extension where K has characteristic
p >0 and let c F. Then
i. K(c) / K is separable algebraic if and only if for all A S
(F/K), A(c) = A(c p
).
ii. K(c) / K is pinely inseparable if and only if there exists a
non-negative integer e such that for all A S (F/K),
A (cpe
) = A(1).
iii. K(c) / K is inseparable if and only if there exists
A S (F/K) such that A(c) < A(c p
) and there exists a
positive integer e such that for all A S (F/K)
A(c p e
) = A(c p e-1
) [87].
Definition 2.3.2: A non-empty set (R, +, ) with two binary operations
‘+’and ' ' is said to be a biring if R =R1 R2 where
R1 and R2 are proper subsets of R and
i. (R1, +, ) is a ring.
ii. (R2, +, ) is a ring.](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-67-320.jpg)

![CHAPTER 3 FUZZY NUMBERS
63
Chapter (3)
FUZZY REAL NUMBERS
The concept of a fuzzy numbers arises from the fact that many
quantifiable phenomena do not end themselves to being characterized in
terms of absolutely precise numbers. For example most of us have
watches that are at least somewhat inaccurate, so we might say that the
time is now “about two o’clock.” Or , we may not wish to pin ourselves
down to an exact schedule and, thus, issue an invitation to dinner for
“around six-thirty.” In a grocery store, we are satisfied if a bunch of
banana weight “approximately four bounds.” Thus, a fuzzy number is one
which is described in terms of a number word and a linguistic modifier,
such as approximately, nearly, or around [4].
Intuitively, we can see that the concept captured by the linguistic
expression approximately six is fuzzy, because it includes some number
values on either side of its central value of six. Although the central value
is fully compatible with this concept, the number around the central value
are compatible with it to lesser degree. Intuitively, we feel that the degree
of compatibility of each number with the concept should express, in some
way dependent on the context, its proximity to the central value. That is,
the concept can be captured by a fuzzy set defined on the set of real
numbers. Its membership function should assign the degree of 1 to the
central value and degrees to other numbers that reflect their proximity to
the central value according to some rules. The membership function
should thus decrease from 1 to 0 on both sides of the central value. Fuzzy
sets of this kind are called fuzzy numbers [7].
It is not difficult to see that fuzzy number plays an important role in
many application, including decision making, approximate reasoning,
fuzzy control, and statistic with imprecise probabilities. We can imagine,
for example, a decision-making situation in which a stock analyst
concludes that if a particular stock reaches about $50, then the fund
manager should sell approximately half of her available shares. Before we
explore the implication of this concept, we must define the concept of
fuzzy number more precisely[10].](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-69-320.jpg)
![CHAPTER 3 FUZZY REAL NUMBERS
64
3.1 Concept of Fuzzy Number
3.1.1 Interval
When interval is defined on real number , this interval is said to
be a subset of . For instance, if interval is denoted as A = [a1, a3] a1, a3
, a1 < a3, we may regard this as one kind of sets. Expressing the
interval as membership function is shown in the following (Fig 3.1) :
A(x) =
3
31
1
,0
,1
,0
ax
axa
ax
If a1 = a3, this interval indicates a point. That is, [a1, a1] = a1
3.1.2 Fuzzy Number
Fuzzy number is expressed as a fuzzy set defining a fuzzy interval
in the real number . Since the boundary of this interval is ambiguous, the
interval is also a fuzzy set. Generally a fuzzy interval is represented by
two end points a1 and a3 and a peak point a2 as (a1, a2, a3 ) (Fig 3.2). The
a-cut operation can be also applied to the fuzzy number. If we denote a-
cut interval for fuzzy number A as Aα, the obtained interval Aα is defined
as
Aα = [a1
(α)
, a3
(α)
]
Fig 3.1: Interval A=[a1,a3]](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-70-320.jpg)
![CHAPTER 3 FUZZY REAL NUMBERS
65
We can also know that it is an ordinary crisp interval (Fig 3.3). We
review here the definition of fuzzy number given in section 1.5.4.
Definition (Fuzzy number) is a fuzzy set satisfying the following
conditions
- Convex fuzzy set
- Normalized fuzzy set
- It’s membership function is piecewise continuous.
- It is defined on the real numbers.
Fuzzy number should be normalized and convexed. Here
the condition of normalization implies that maximum
membership value is 1.
x , µA(x) = 1
The convex condition is that the line by α-cut is continuous and α-
cut interval satisfies the following relation.
Aα = [a1
(α)
, a3
(α)
]
(α′ < α) (a1
(α′)
≤ a1
(α)
, a3
(α′)
≥ a3
(α)
)
Fig 3.2: Fuzzy number A=[a1,a2,a3]](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-71-320.jpg)
![CHAPTER 3 FUZZY REAL NUMBERS
66
The convex condition may also be written as,
(α′ < α) (A α A α′)
3.1.3 Operation of Interval
Operation of fuzzy number can be generalized from that of
crisp interval. Let’s have a look at the operations of interval.
a1, a3, b1, b3
A = [a1, a3], B = [b1, b3]
Assuming A and B as numbers expressed as interval, main
operations of interval are
i. Addition
[a1, a3] (+) [b1, b3] = [a1 + b1, a3 + b3]
ii. Subtraction
[a1, a3] (-) [b1, b3] = [a1 - b3, a3 - b1]
Fig 3.3: α-cut of fuzzy number (α’ < α) (A α A α′)](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-72-320.jpg)
![CHAPTER 3 FUZZY REAL NUMBERS
67
iii. Multiplication
[a1, a3] () [b1, b3] = [a1 b1 a1 b3 a3 b1 a3
b3, a1 b1 a1 b3 a3 b1 a3 b3]
iv. Division
[a1, a3] (/) [b1, b3] = [a1 / b1 a1 / b3 a3 / b1 a3 / b3,
a1 / b1 a1 / b3 a3 / b1 a3 / b3]
excluding the case b1 = 0 or b3 = 0
v. Inverse interval
[a1, a3]
- 1
= [1 / a1 1 / a3, 1 / a1 1 / a3]
excluding the case a1 = 0 or a3 = 0
When previous sets A and B are defined in the positive real
number, the operations of multiplication, division, and inverse
interval are written as,
iii.' Multiplication
[a1, a3] () [b1, b3] = [a1 b1, a3 b3]
iv.' Division
[a1, a3] (/) [b1, b3] = [a1 / b3, a3 / b1]
v.' Inverse Interval
[a1, a3]
- 1
= [1 / a3, 1 / a1]
vi. Minimum
[a1, a3] () [b1, b3] = [a1 b1, a3 b3]
vii. Maximum
[a1, a3] () [b1, b3] = [a1 b1, a3 b3]](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-73-320.jpg)
![CHAPTER 3 FUZZY REAL NUMBERS
68
Example 3.1: There are two intervals A and B,
A = [3, 5], B = [-2, 7]
Then following operation might be set.
A(+)B = [3-2, 5+7] = [1, 12]
A(-)B = [3-7, 5 - (-2)] = [-4, 7]
A()B = [3(-2) 375(-2) 57, 3(-2) …]
= [-10, 35]
A(/)B = [3/(-2) 3/75/(-2) 5/7, 3/(-2) …]
= [5/7, 2.5]
7
1
,
2
1
7
1
)2(
1
,
7
1
)2(
1
]7,2[ 11
B
3.2 Operation of Fuzzy Number
3.2.1 Operation of α-cut Interval
We referred to α-cut interval of fuzzy number A = [a1, a3] as crisp
set.
Aα = [a1
(α)
, a3
(α)
], α [0, 1], a1, a3, a1
(α)
, a3
(α)
So A α is a crisp interval. As a result, the operations of interval
reviewed in the previous section can be applied to the α-cut interval Aα.
If α-cut interval Bα of fuzzy number B is given
B = [b1, b3], b1, b3
Bα = [b1
(α)
, b3
(α)
], α [0, 1], b1
(α)
, b3
(α)
,](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-74-320.jpg)
![CHAPTER 3 FUZZY REAL NUMBERS
69
operations between Aα and Bα can be described as follows :
[a1
(α)
, a3
(α)
] (+) [b1
(α)
, b3
(α)
] = [a1
(α)
+ b1
(α)
, a3
(α)
+ b3
(α)
]
[a1
(α)
, a3
(α)
] (- ) [b1
(α)
, b3
(α)
] = [a1
(α)
- b3
(α)
, a3
(α)
- b1
(α)
]
These operations can be also applicable to multiplication and
division in the same manner.
3.2.2 Operation of Fuzzy Number
Previous operations of interval are also applicable to fuzzy number.
Since outcome of fuzzy number (fuzzy set) is in the shape of fuzzy
set, the result is expressed in membership function.
x, y, z
i. Addition: A (+) B
))()(()()( yxz BA
yxz
BA
ii. Subtraction: A (-) B
))()(()()( yxz BA
yxz
BA
iii. Multiplication: A () B
))()(()()( yxz BA
yxz
BA
iv. Division: A (/) B
))()(()(
/
(/) yxz BA
yxz
BA
v. Minimum: A () B
))()(()()( yxz BA
yxz
BA
vi. Maximum: A () B
))()(()()( yxz BA
yxz
BA
](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-75-320.jpg)
![CHAPTER 3 FUZZY REAL NUMBERS
70
We can multiply a scalar value to the interval. For instance,
multiplying a ,
a[b1, b3] = [a b1 a b3, a b1 a b3]
Example 3.2
There is a scalar multiplication to interval. Note the scalar value is
negative.
-4.15 [-3.55, 0.21] = [(-4.15) (-3.55) (-4.15) 0.21, (-4.15)
(-3.55) (-4.15) 0.21]
= [14.73 -0.87, 14.73 -0.87]
= [-0.87, 14.73]
We can also multiply scalar value to α-cut interval of fuzzy
number.
[0, 1], b1
(α)
, b3
(α)
a[b1
(α)
, b3
(α)
] = [a b1
(α)
a b3
(α)
, a b1
(α)
a b3
(α)
]
3.2.3 Examples of Fuzzy Number Operations
Example 3.3 : Addition A(+)B
For further understanding of fuzzy number operation, let us
consider two fuzzy sets A and B. Note that these fuzzy sets are
defined on discrete numbers for simplicity.
A = {(2, 1), (3, 0.5)}, B = {(3, 1), (4, 0.5)}
First of all our concern is an addition between A and B. To induce A(+)B,
for all x A, y B, z A(+)B, we check each case as follows ( Fig. 3.4)
i. for z < 5,](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-76-320.jpg)




![CHAPTER 3 FUZZY REAL NUMBERS
76
Definition(Triangular fuzzy number) It is a fuzzy number
represented with three points as follows:
A = (a1, a2, a3)
This representation is interpreted as membership functions(Fig3.6).
3
32
23
3
21
12
1
1
)(
,0
,
,
,0
)(
ax
axa
aa
xa
axa
aa
ax
ax
xA
Now if you get crisp interval by α-cut operation, interval Aa shall be
obtained as follows [0, 1].
From
23
)(
33
12
1
)(
1
,
aa
aa
aa
aa
we get
a1
(α)
= (a2 − a1)α + a1
Fig 3.6: Triangular fuzzy number A=(a1,a 2,a3)](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-82-320.jpg)
![CHAPTER 3 FUZZY REAL NUMBERS
77
a3
(α)
= − (a3 − a2)α + a3
Thus
Aα = [a1
(α)
, a3
(α)
]
= [(a2 − a1)α + a1, − (a3 − a2)α + a3]
Example 3.6 :
In the case of the triangular fuzzy number A = (−5, −1, 1) (Fig 3.7),
the membership function value will be,
1,0
11,
2
1
15,
4
5
5,0
)()(
x
x
x
x
x
x
xA
-cut interval from this fuzzy number is
12
2
1
54
4
5
x
x
x
x
Fig 3.7: =0.5 cut of triangular fuzzy number A=(-5,-1,1)](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-83-320.jpg)
![CHAPTER 3 FUZZY REAL NUMBERS
78
Aα = [a1
(α)
, a3
(α)
] = [4α − 5, −2α + 1]
If α = 0.5, substituting 0.5 for α, we get A0.5
A0.5 = [a1
(0.5)
, a3
(0.5)
] = [−3, 0]
3.3.1.2 Operations on Triangular Fuzzy Number
Some important properties of operations on triangular fuzzy
number are summarized.
(1) The results from addition or subtraction between triangular
fuzzy numbers result also triangular fuzzy numbers.
(2) The results from multiplication or division are not triangular
fuzzy numbers.
(3) Max or min operation does not give triangular fuzzy number.
But we often assume that the operational results of multiplication
or division to be TFNs as approximation values.
1) Operation of triangular fuzzy number
First, consider addition and subtraction. Here we need not use
membership function. Suppose that triangular fuzzy numbers A and
B are defined as,
A = (a1, a2, a3), B = (b1, b2, b3)
i. Addition
A(+)B = (a1, a2, a3) (+) (b1, b2, b3) : triangular fuzzy number
= (a1+b1,a2+b2,a3+b3)](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-84-320.jpg)

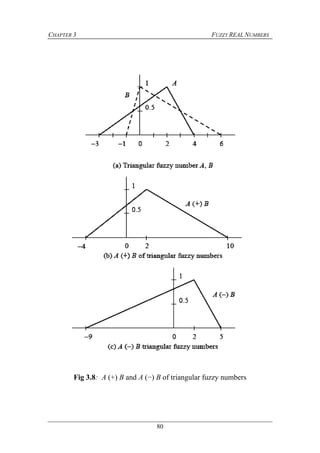
![CHAPTER 3 FUZZY REAL NUMBERS
81
2) Operations with α-cut
Example 5.8:
α-level intervals from α-cut operation in the above two triangular
fuzzy numbers A and B are
Aα = [a1
(α)
,a3
(α)
] = [(a2 − a1) α + a 1, − (a3 − a2) α + a3]
= [5α −3, −2α +4]
Bα = [b1
(α)
,b3
(α)
] = [(b2 − b1) α + b 1, − (b3 − b2) α + b3]
= [α −1, −6α +6]
Performing the addition of two α-cut intervals Aα and Bα,
Aα (+) Bα = [6α − 4, −8α + 10]
Especially for α = 0 and α = 1,
A0 (+) B0 = [−4, 10]
A1 (+) B1 = [2, 2] = 2
Three points from this procedure coincide with the three points of
triangular fuzzy number (-4, 2, 10) from the result A(+)B given in
the previous example.
Likewise, after obtaining Aα(−)Bα, let’s think of the case when α =
0 and α = 1.
Aα (−) Bα = [11α − 9, −3α + 5]
Substituting α = 0 and α = 1 for this equation,
A0 (−) B0 = [−9, 5]
A1 (−) B1 = [2, 2] = 2
These also coincide with the three points of A(−)B = (−9, 2, 5).](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-87-320.jpg)

![CHAPTER 3 FUZZY REAL NUMBERS
83
A(+)B = yxg
[A(2) B(6), A(3) B(5), A(3.5)
B(4.5),…]
= [1 0, 0.5 1/6, 0.25 0.25,…]
= [0, 1/6, 0.25, …]
A new general method giving all details about addition operation offered
as follows :
we can construct the pyramid (Fig. 3.9) representing the
membership of the points (x, y) where,
,,,
~
,,,
~
321321 bbbByaaaAx
its base is the rectangular fuzzy domain
,
~~
,
~
,
~
,
~~
BAyxByAxyxBA
with vertices 0,,,0,,,0,,,0,, 13333111 babababa , the center of the
base is the point 0,, 22 ba . And its height is parallel to the axis μ
which is taken perpendicular to the base, wit length 1.
1b
2b
3b
1a 2a 3a
x
0,, 13 ba
0,, 33 ba
0,, 31 ba
0,, 11 ba
0,, 22 ba
1
1,, 22 ba
A
~
B
~
y
Fig 3.9 : BA
~~
](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-89-320.jpg)






![CHAPTER 3 FUZZY REAL NUMBERS
90
Calculating multiplication A () B of A and B, z = x y = 8 is
possible
when z = 2 4 or z = 4 2
A()B = 8yx
[A(2) B(4), A(4) B(2),…]
= [1 1, 0 0,…]
= 1
Also when z = x y = 12, 3 4, 4 3, 2.5 4.8, . are possible.
A()B = 12yx
[A(3) B(4), A(4) B(3), A(2.5)
B(4.8),…]
= [0.5 1, 0 0.5/6, 0.75 0.6,…]
= [0.5, 0, 0.6, …]
= 0.6
From this kind of method, if we come by membership function for
all z A () B, we see fuzzy number as in Fig 3.12. However, since this
shape is in curve, it is not a triangular fuzzy number. For convenience, we
can express it as a triangular fuzzy number by approximating A () B.
24,8,2 BA
We can see that two end points and one peak point are used in this
approximation.
Fig 3.12: Multiplication A () B of two triangular fuzzy numbers](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-96-320.jpg)


![CHAPTER 3 FUZZY REAL NUMBERS
93
3
2
1
: y
which gives the value of at any point 64 y of the number xy=12
at
4
1
5.5 y
69722.06.4,6.212.max
~~
1212 yxBA
To compare with the - cut method: fig.3.14
12xy
Aα = [(2 − 1)α +1, − (4−2)α +4]
= [α +1, −2 α +4]
Bα = [(4 − 2)α +2, − (6−4)α +6]
A
~
B
~
Fig. 3.13: Fuzzy number xy=12
1 2 4
2
4
6
1
0.2.1
0,2,4
0,6,4 0,6,1
0,4,2
0,6,2
0,3,4
xy = 12
(2.6,4.6,0.69722)
(2,4,1)
4
12
1
4,3
x
y](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-99-320.jpg)
![CHAPTER 3 FUZZY REAL NUMBERS
94
= [2α +2, −2 α +6]
Aα () Bα = [α +1, −2 α +4] () [2α +2, −2 α +6]
= [(α +1)(2α +2), (−2α + 4) (−2α +6)]
= [2α2
+4α +2, 4α2
−20α +24]
but 12xy 4α2
−20α +24
1224204 2
012204 2
0352
2
12255
2
135
69722.0
2
6055.35
69722.01
To compare with the three point representation method:
The equation of the line A2A3 gives:
16
1
248
01
24
0
x
75.0
16
12
16
24
16
12
16
24
16
1
2 x
0 2 8 12 24
1
Three point method.
0.75
Pyramid and -cut method.
0.69722
A1
A2
A3
l
Fig.3.14 comparison between pyramid method and other
h d](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-100-320.jpg)

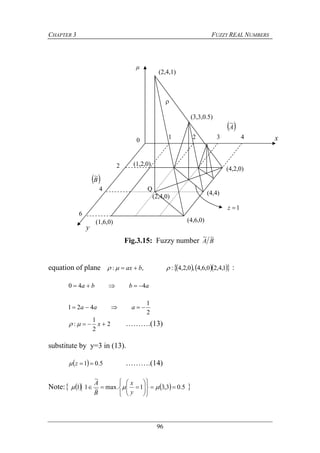
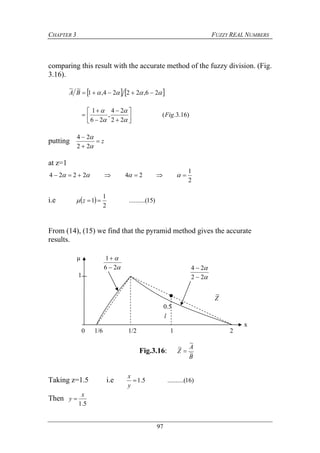

![CHAPTER 3 FUZZY REAL NUMBERS
99
Lemma 3.1
The distributive law,
A·(B+C)=A·B+A·C
does not always hold on the set of all fuzzy real numbers.
Now we are going to show that by some examples:
Example 3.15 :
let A=[1+α, 3- α], B=[-4+2 α, -1- α], C=[1+ α, 4-2 α]
Solution :
L.H.S = A·(B+C) = [1+α, 3- α]([-3+3α, 3-3α])
= [(3-α)(-3+3α), (3-α)(3-3α)]
= [-9+12α-3α2
, 9-12α+3α2
]……………(1)
0
α
x
1
-
Fig. 3.17
(-,0,)
α
a
1 a1
x
1
a
a
,1,
1](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-105-320.jpg)
![CHAPTER 3 FUZZY REAL NUMBERS
100
R.H.S = A·B+A·C = [(3-α)(-4+2α), (1+α)(-1-α)]+[(1+α)(1+α),(3-α)(4-
2α)]
= [-12+10α-2α2
, -1-2α-α2
]+[1+2α+α2
, 12-10α+2α2
]
= [-11+12α-α2
, 11-12α+α2
]…………….(2)
from (1) & (2) A·(B+C) ≠ A·B+A·C
Example 3.16 :
let A=[2+α, 5-2α], B=[-6+3α, -1-2α], C=[1+2α, 6-3α]
Solution :
L.H.S = A·(B+C) = [2+α, 5-2α]([-5+5α, 5-5α])
= [(5-2α)(-5+5α), (5-2α)(5-5α)]
= [-25+35α-10α2
, 25-35α+10α2
]……………(3)
R.H.S = A·B+A·C = [2+α, 5-2α] [-6+3α, -1-2α]+[2+α, 5-2α] [1+2α, 6-3α]
= [-30+27α-6α2
, -2-5α-2α2
]+[2+5α+2α2
, 30-27α+6α2
]
= [-28+32α-4α2
, 28-32α+4α2
]…………….(4)
from (3) & (4) A·(B+C) ≠ A·B+A·C
3.3.2 Trapezoidal Fuzzy Real Number
Another shape of fuzzy number is trapezoidal fuzzy number. This
shape is originated from the fact that there are interval of points
whose membership degree is maximum (α = 1).
Definition (Trapezoidal fuzzy number) we can define trapezoidal
fuzzy number A as
A = (a1, a2, a3, a4)
The membership function of this fuzzy number will be interpreted
as follows(Fig 3.18).](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-106-320.jpg)
![CHAPTER 3 FUZZY REAL NUMBERS
101
4
43
34
4
32
21
12
1
1
)(
,0
,
,1
,
,0
)(
ax
axa
aa
xa
axa
axa
aa
ax
ax
xA
Fig 3.18: Trapezoidal fuzzy number A = (a1, a2, a3, a4)
α-cut interval for this shape is written below.
α [0, 1]
Aα = [(a2− a1 )α + a1, − (a4 − a3)α + a4]
When a2 = a3, the trapezoidal fuzzy number coincides with
triangular one.
3.3.2.1 Operations on Trapezoidal Fuzzy Numbers
Let’s talk about the operations of trapezoidal fuzzy number as in
the triangular fuzzy number,
1) Addition and subtraction between two trapezoidal fuzzy numbers
become trapezoidal fuzzy number.](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-107-320.jpg)
![CHAPTER 3 FUZZY REAL NUMBERS
102
2) Multiplication, division, and inverse need not to be trapezoidal
fuzzy number.
3) Max and Min of fuzzy number is not always in the form of
trapezoidal fuzzy number.
But in many cases, the operation results from multiplication or
division are approximated trapezoidal shape. As in triangular fuzzy
number, addition and subtraction are simply defined, and
multiplication and division operations should be done by using
membership functions.
i. Addition
A(+)B = (a1, a2, a3, a4) (+) (b1, b2, b3, b4)
= (a 1+ b1, a 2+ b2, a 3+ b3, a4 +b4)
ii. Subtraction
A(−)B = (a1 −b4, a2 −b3, a3 −b2 , a4 −b1)
Example 3.17: Multiplication
Multiply two trapezoidal fuzzy numbers as follows:
A = (1, 5, 6, 9)
B = (2, 3, 5, 8)
For exact value of the calculation, the membership functions shall
be used and the result is described in Fig 3.19. For the
approximation of operation results, we use α-cut interval.
Aα = [4α + 1, −3α + 9]
Bα = [α + 2, −3α + 8]
Since, for all α [0, 1], each element for each interval is positive,
multiplication between α-cut intervals will be](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-108-320.jpg)
![CHAPTER 3 FUZZY REAL NUMBERS
103
Aα () Bα = [(4α +1)(α +2), (−3α +9)( −3α +8)]
= [4α2
+9α +2, 9α2
− 51α +72]
If α = 0,
A0 () B0 = [2, 72]
If α = 1,
A1 () B1 = [4+9+2, 9−51+72]
= [15, 30]
So using four points in α = 0 and α = 1, we can visualize the
approximated value as trapezoidal fuzzy number as Fig 3.19.
72,30,15,2 BA
Fig 3.19: Multiplication of trapezoidal fuzzy number A () B](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-109-320.jpg)

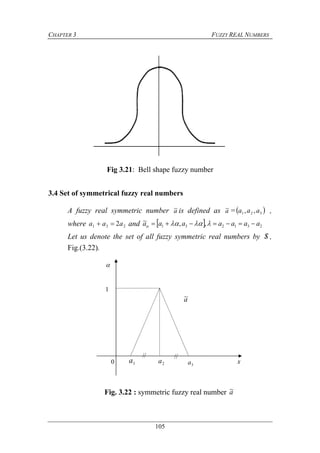






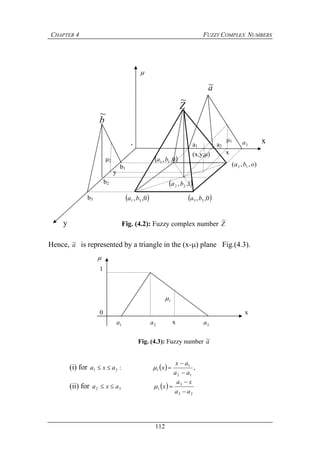



![CHAPTER 4 FUZZY COMPLEX NUMBERS
116
4.2 Operation On Fuzzy Complex Numbers
4.2.1 Addition Of Two Fuzzy Complex Numbers
Let, as before ]y~,x~[Z
~
and
321321 ,,,,,~,~~
nnnmmmnmM or in α-form:
M
~
233121 , mmmmmm , 233121 , nnnnnn (3)
Then,
nmyxMZ ~,~~,~~~
]~~,~~[ nymx
321321321321 ,,,,,,,,, nnnyyymmmxxx
332211332211 ,,,,, nynynymxmxmx ,………(4)
or in α-form
MZ
~~
223333112211 , mxmxmxmxmxmx ,
223333112211 , nynynynynyny …. (5)
Example 4.2:
Let 6,3,1;5,3,2
~
Z , 11,8,7,9,8,6
~
M , find MZ
~~
.
Hence if :
.M
~
Z
~
inmzfind,M
~
i97m,Z
~
i42z
Solution. Shown in Fig. (4.7).
17,11,8,14,11,8
~~
MZ or in α form,
366,131,355,232
~
Z
36,21,25,2 ](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-122-320.jpg)

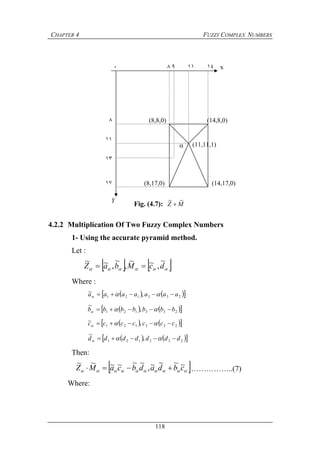

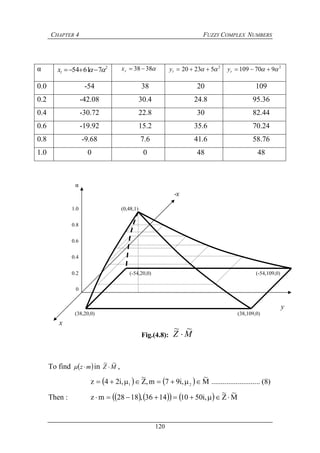




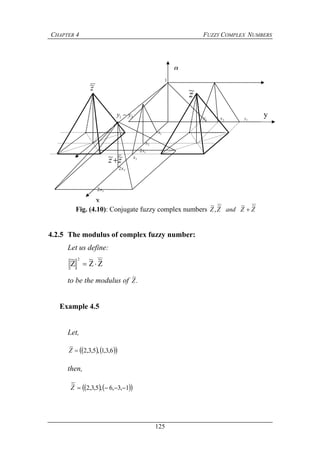




![CHAPTER 4 FUZZY COMPLEX NUMBERS
130
4.2.8 Exponential of fuzzy complex number
4.2.8.1 Exponential of fuzzy real number [4]
let 321 ,,~ aaaa be a fuzzy real number then 321
,,
~ aaaa
eeee
and we can obtain
a
e
~
and a
e
~
.
First method: (Approximate method)
Example 4.7:
Let
)3,2,1(~ a
then,
1. ),,( 321~
eeeea
Shown in Fig. (4.12)
x
1
0
3
e1
e 2
e
Fig.(4.12): Approximate method a
eex
~3,2,1
](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-136-320.jpg)
![CHAPTER 4 FUZZY COMPLEX NUMBERS
131
2. In the α -form: Shown in Fig (4.13)
)](),([)( 233121~
eeeeeeea
Now we can plot )(
~a
e by calculating :
)( 121
eee )( 233
eee
0.0 2.71828 20.85536
0.2 3.65243 17.55257
0.4 4.58659 15.00694
0.6 5.51474 12.46764
0.8 6.45490 9.928351
1.0 7.38905 7.389055
Second method (Accurate method)
]3,1[~ a
x
1
0
2.718 7.38 20.855
Fig. (4.13):Approximate method )(
~a
ex ](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-137-320.jpg)
![CHAPTER 4 FUZZY COMPLEX NUMBERS
132
],[ 31~
eeea
We can plot the curve a
ex
~
31
,, eexx r Shown in Fig.(4.14)
We can find max. error or max. deviation of
a
ex from
a
ex
~
1
ex
3
exr
0 2.71828 20.08356
0.2 3.32011 16.44464
0.4 4.05519 13.46373
0.6 4.95303 11.02317
0.8 6.04964 9.250133
1.00 7.389055 7.389055
7.380 20.0832.71
1
Fig.(4.14): accurate method
a
ex
~
](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-138-320.jpg)

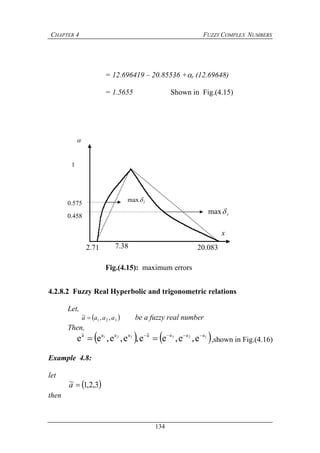
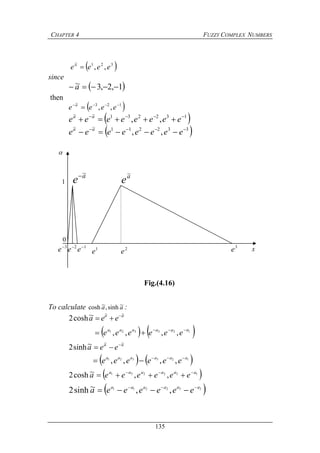





![CHAPTER 4 FUZZY COMPLEX NUMBERS
141
055925
592
1
1
R
4
11
5
4
25
59
2
5
59
20
11
05.05.245.2
20
125
20
49
20
55
9
20
11
3max
R
New remark:
The fuzzy complex number can be written in terms of its fuzzy
modulus and fuzzy argument where:
~
,0
~
~~
erZ ,
~
,0
~
~~
esW ...................................................................(23)
If , ],y~,x~[Z
~
where, ),,(~,,,~
)321321 yyyyxxxx ,
Then,
22~ yxr ,
2
3
2
3
2
2
2
2
2
1
2
1 ,, yxyxyx ,
1
31
2
21
3
11
1
3
2
2
3
111
tan,tan,tan,,tan~
~
tan
~
x
y
x
y
x
y
x
y
x
y
x
y
x
y
,
We can define the division of two complex numbers using (23) as:
~~
,0
~
~
,~
~
,0
~
~
~
~
~
~
~
e
s
r
es
er
W
Z
o
.
Example 4.13:
Find arctan a~ if
3,1,
3
1~a .](https://image.slidesharecdn.com/3202129-151205083948-lva1-app6892/85/Aljabar-Fuzzy-147-320.jpg)


















