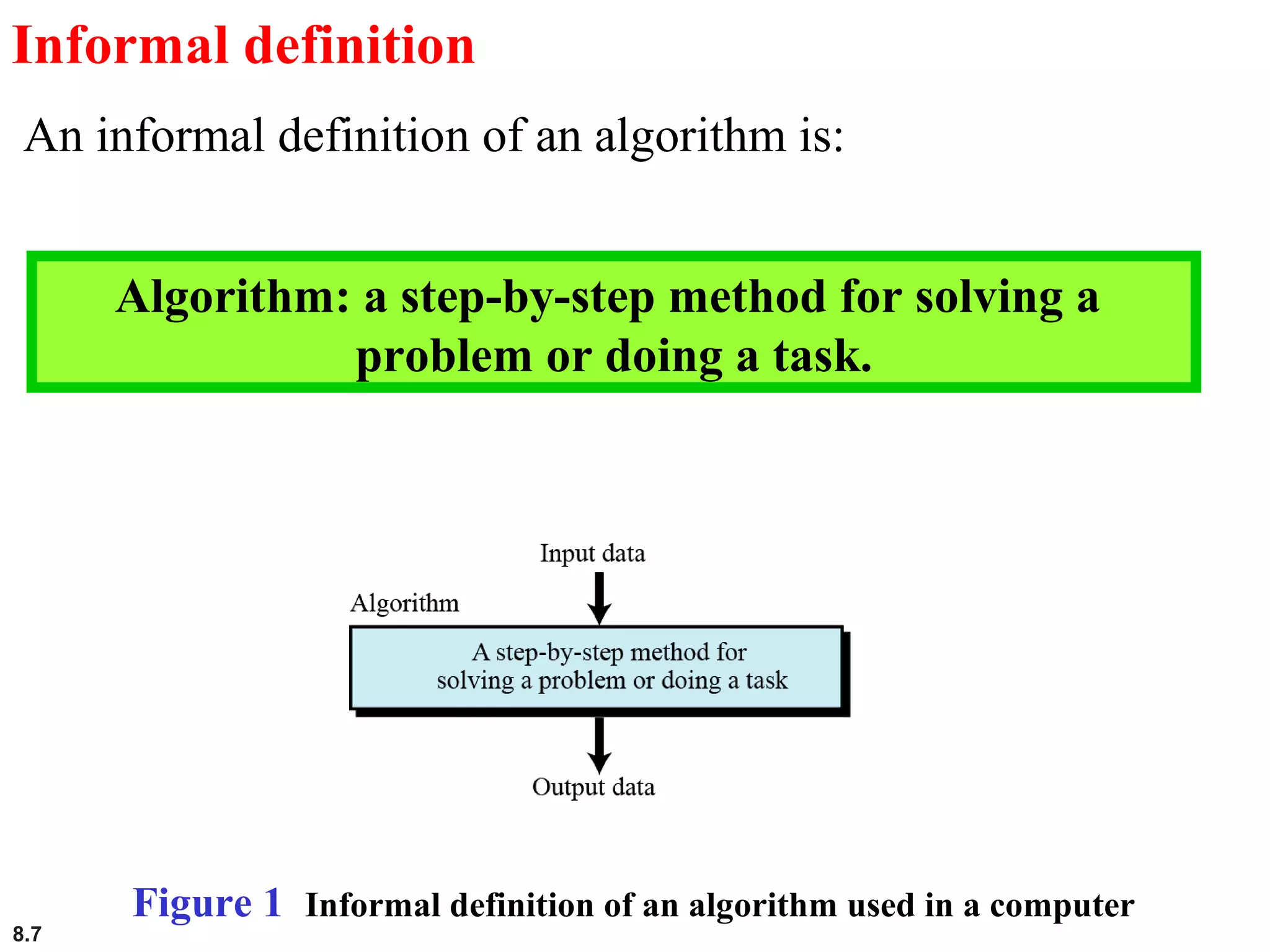
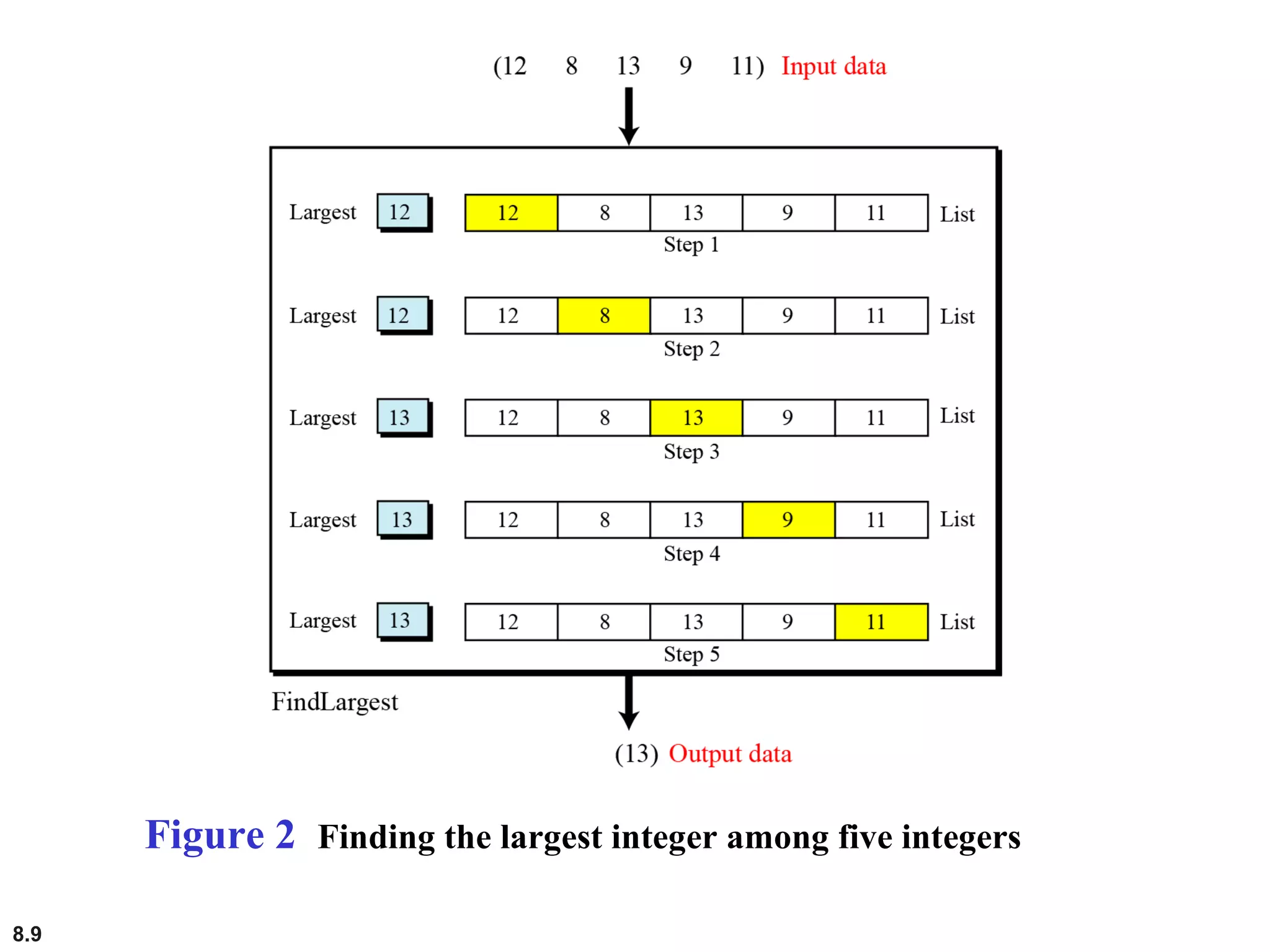
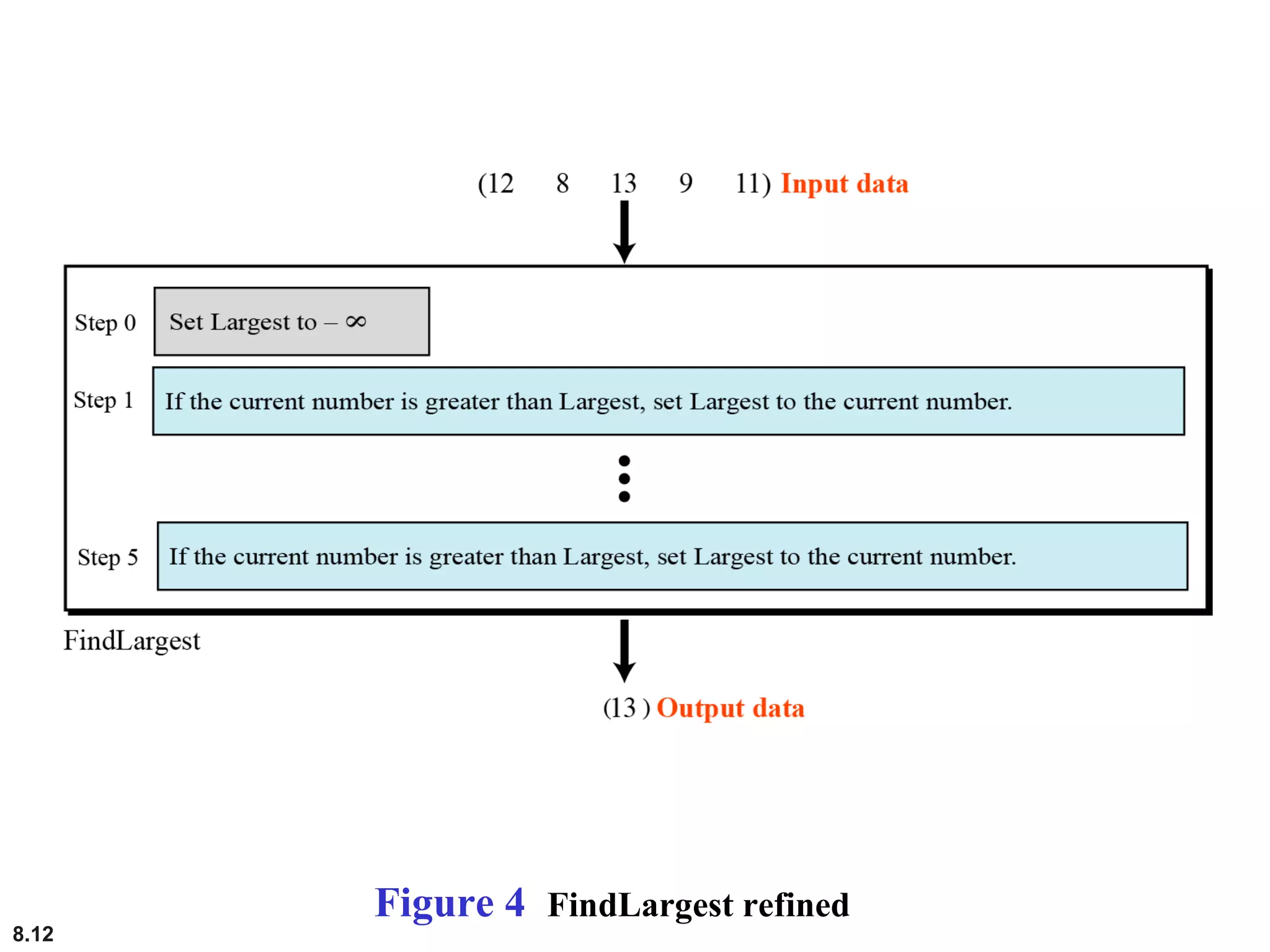
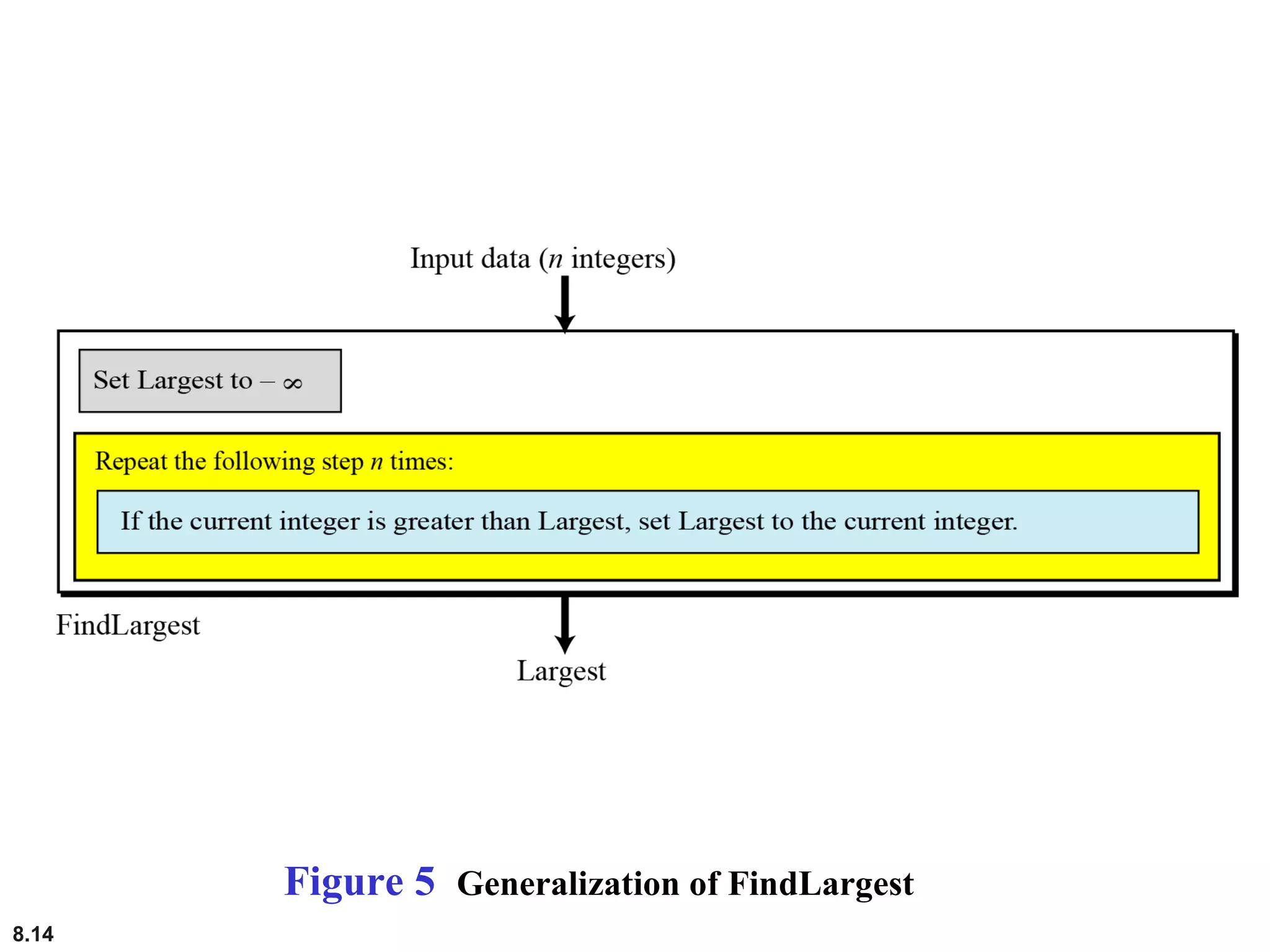
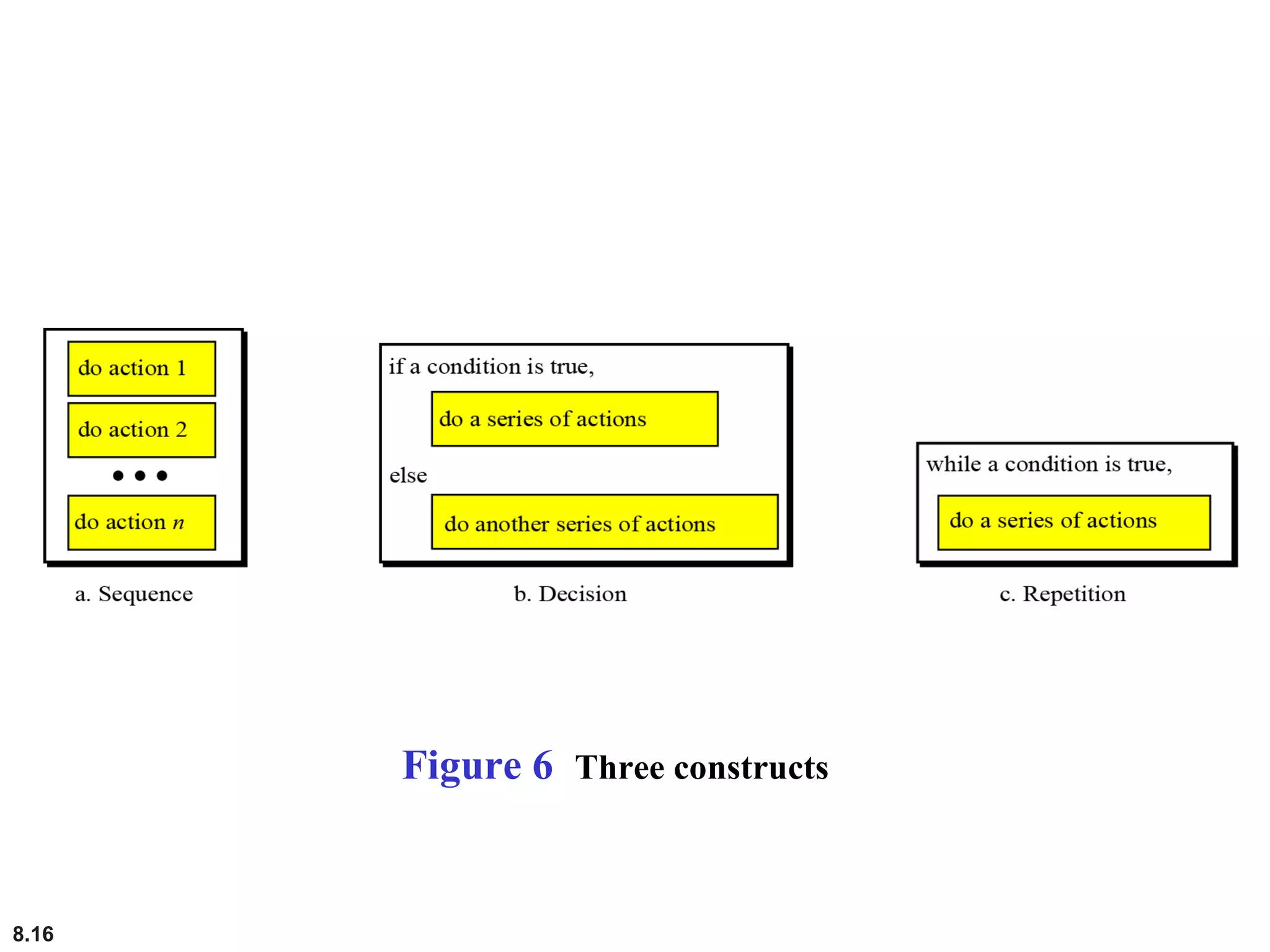
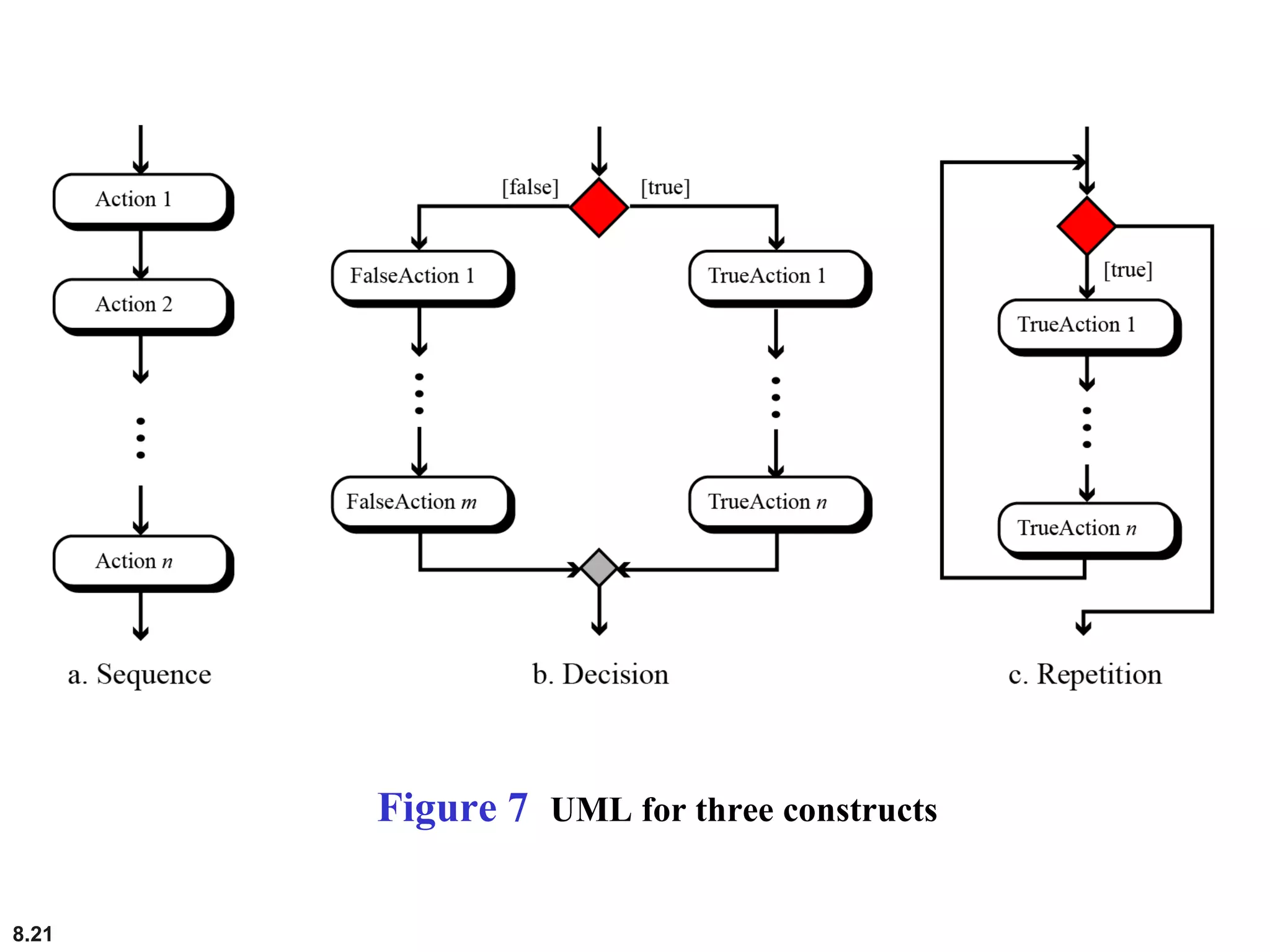
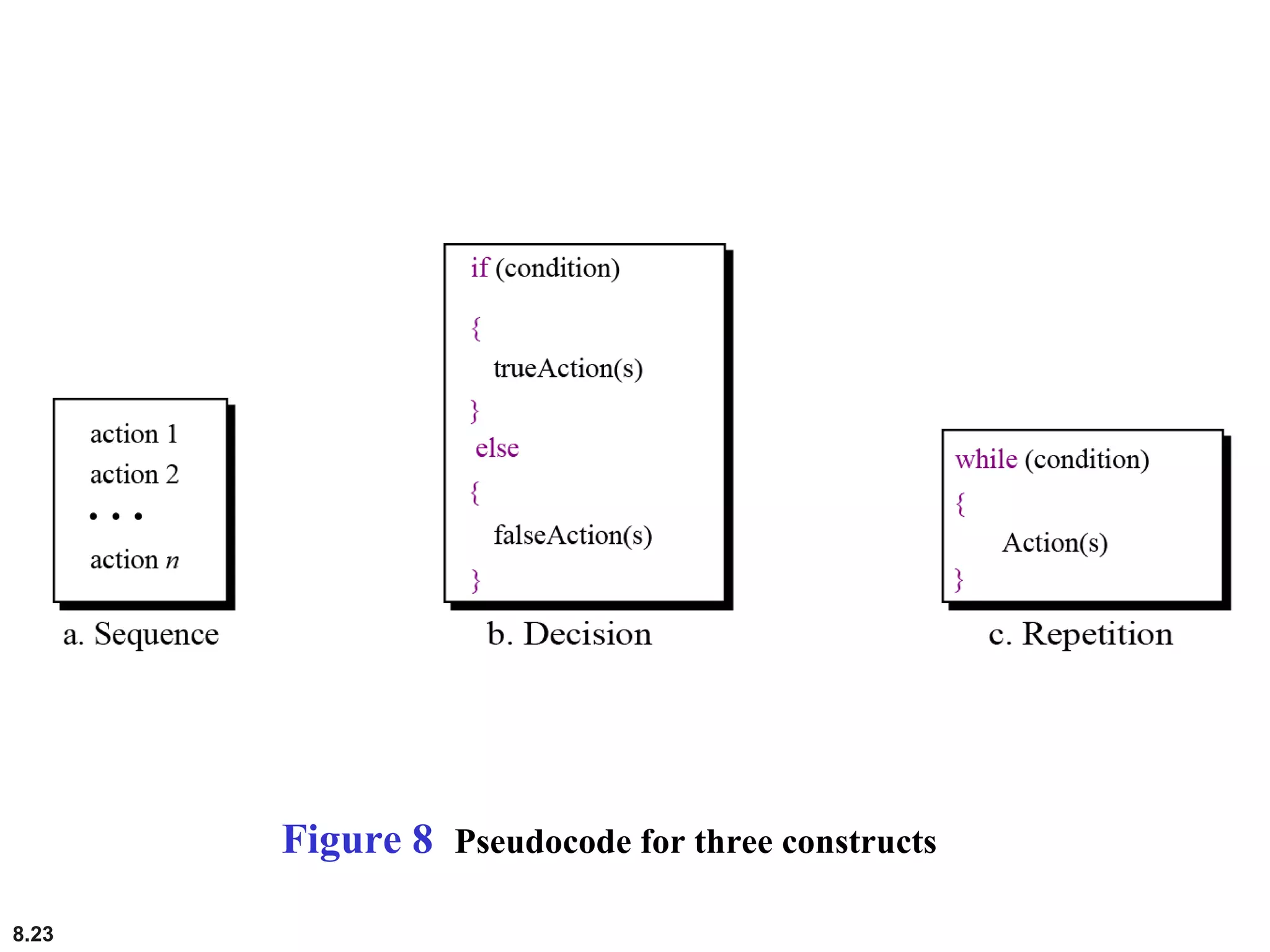
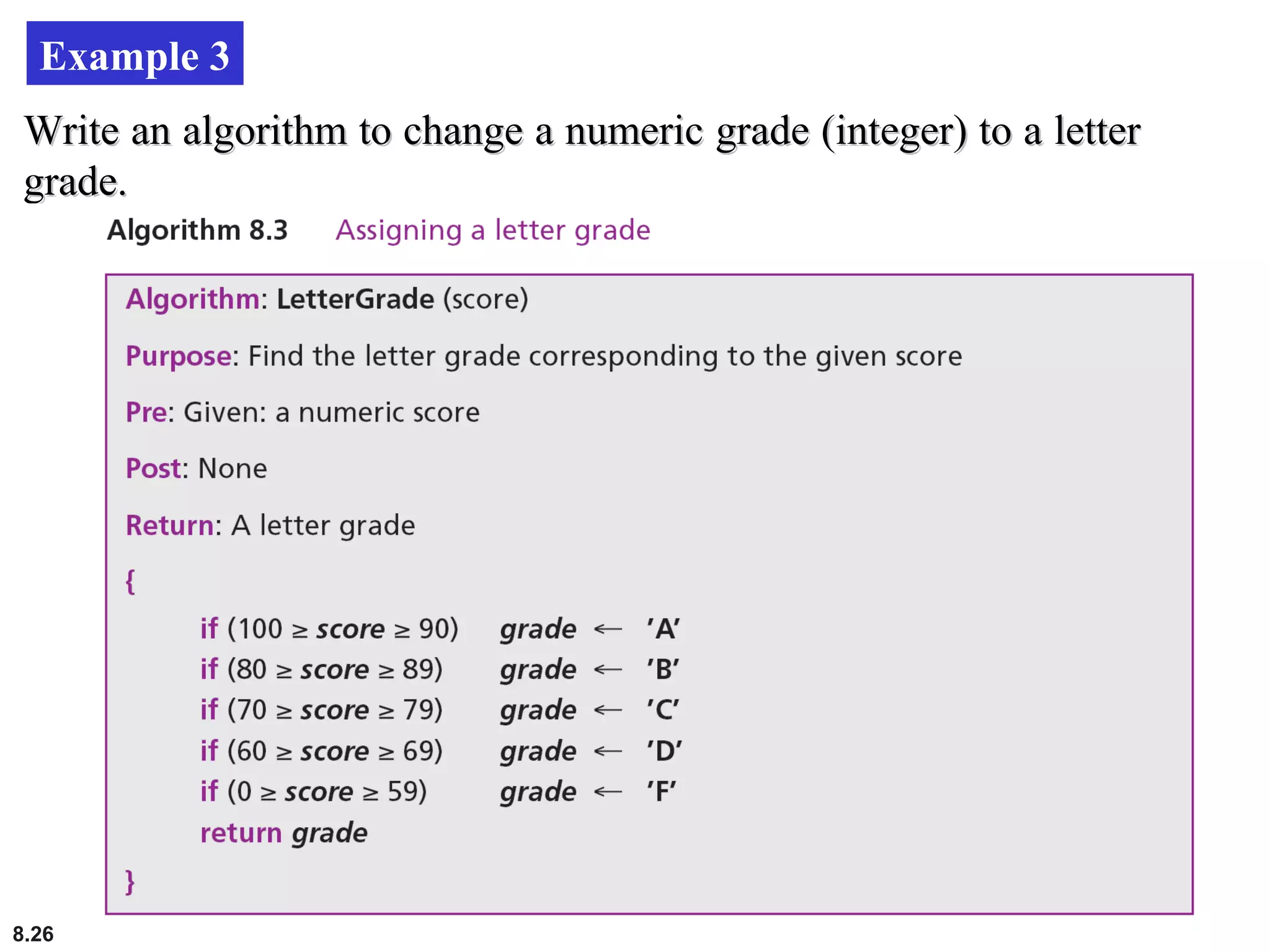
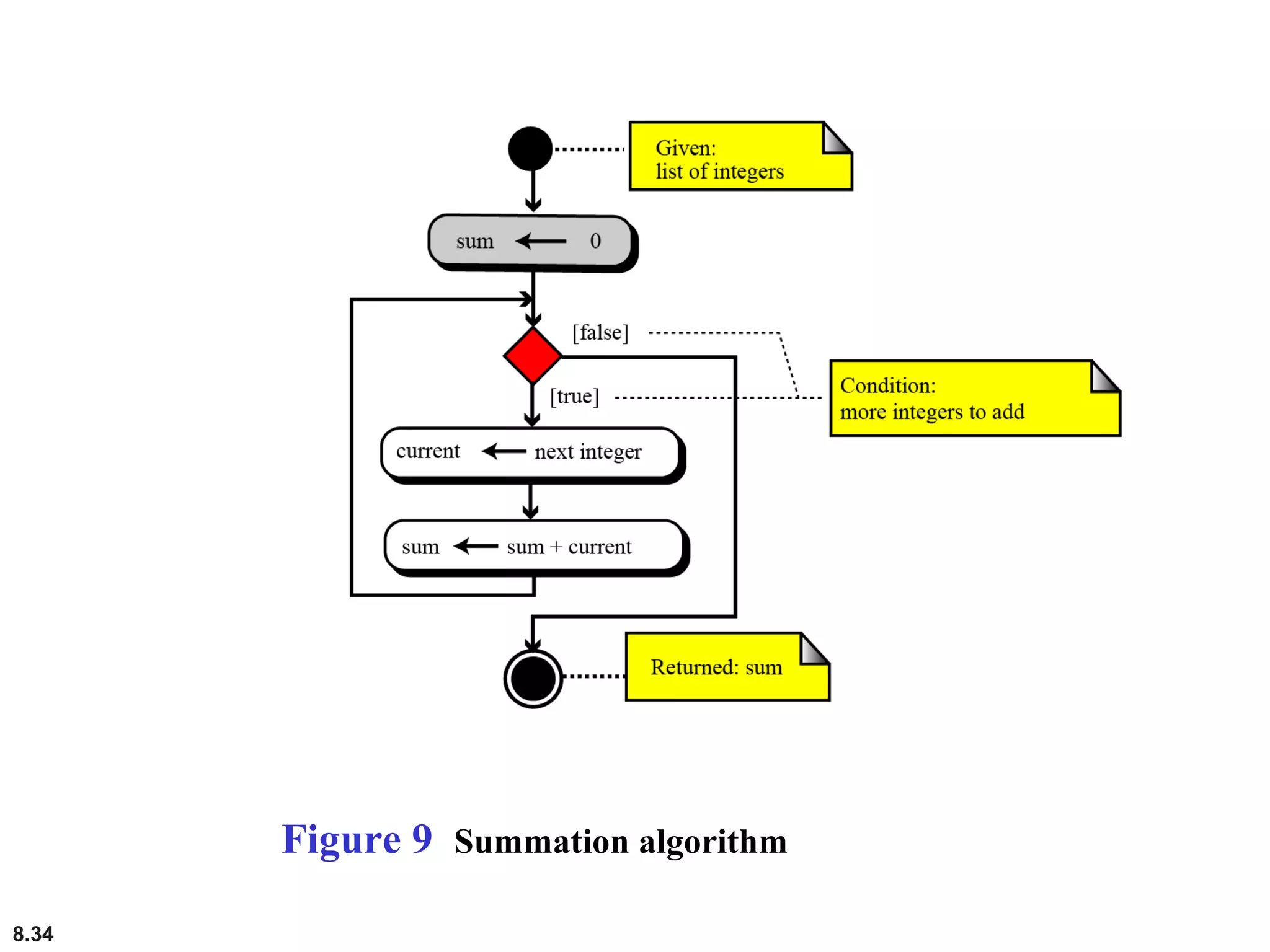
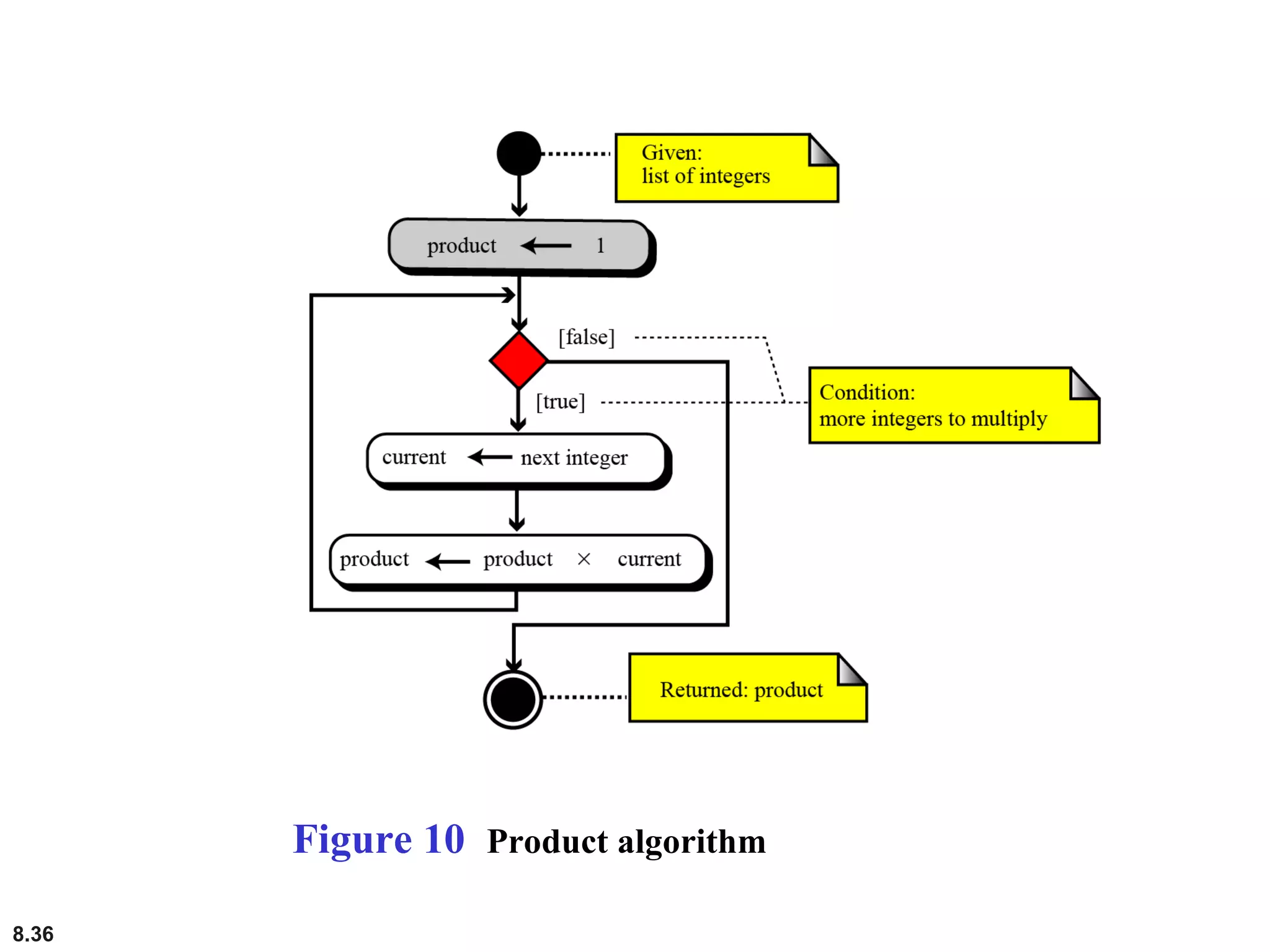
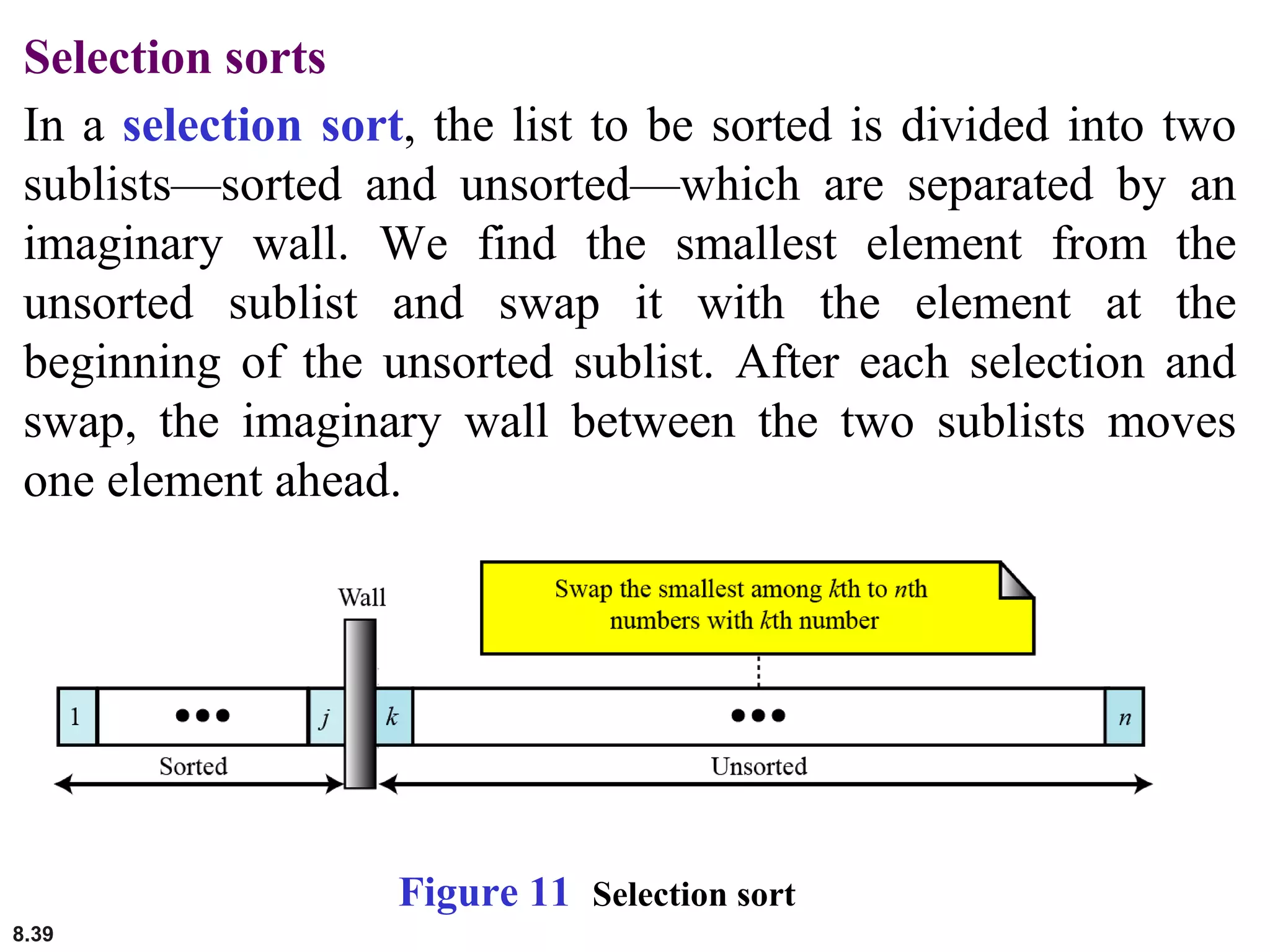
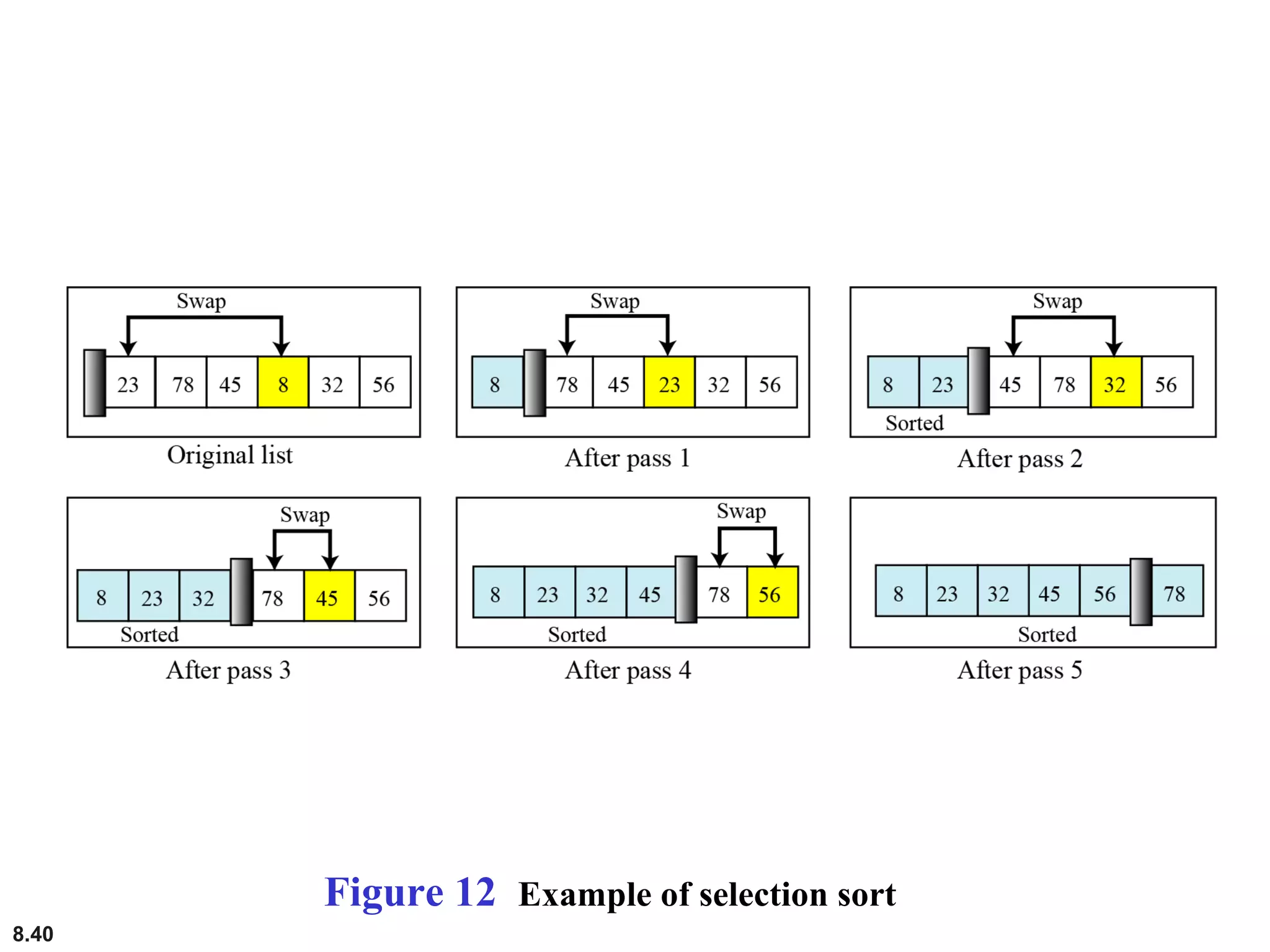
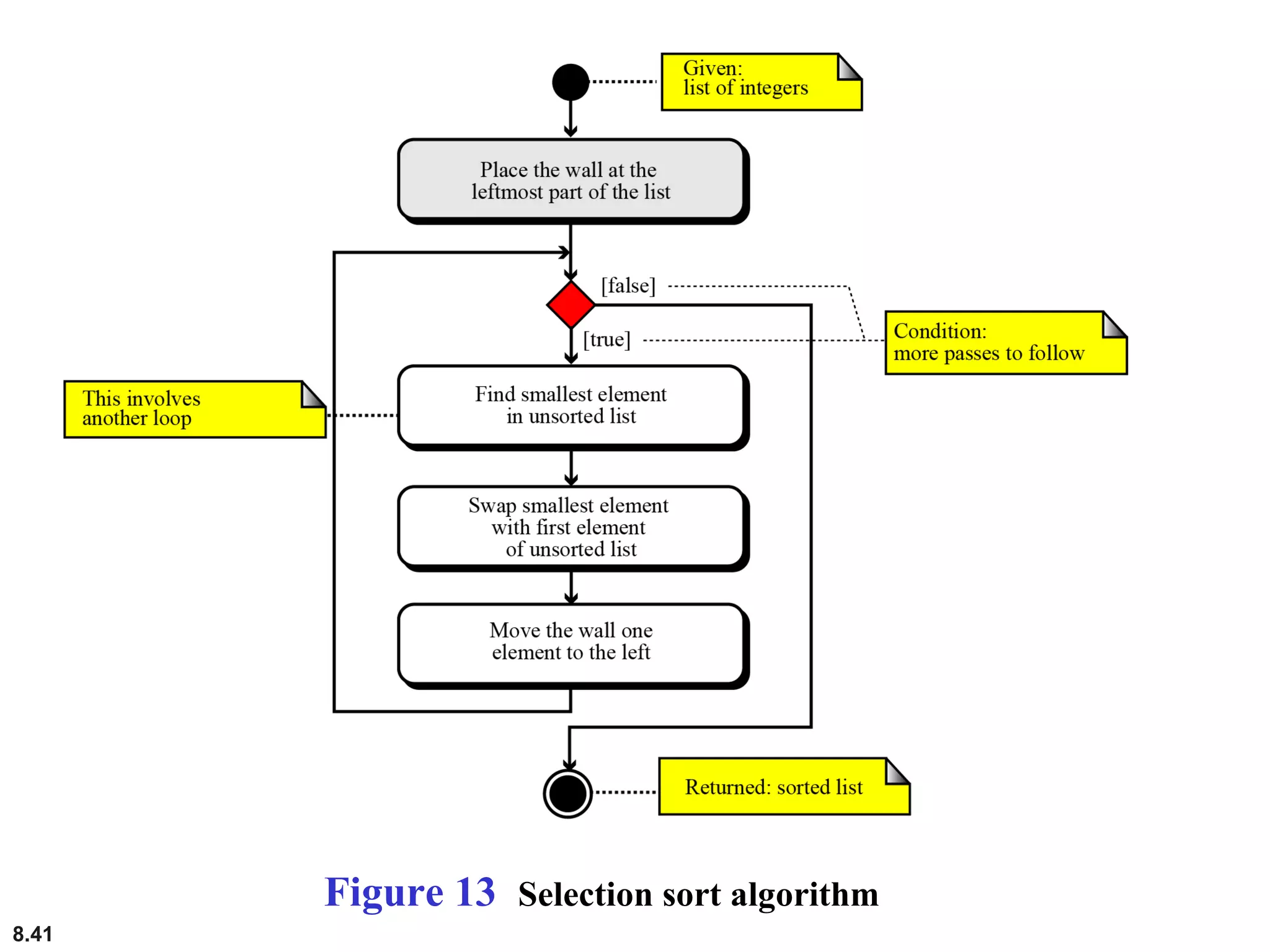
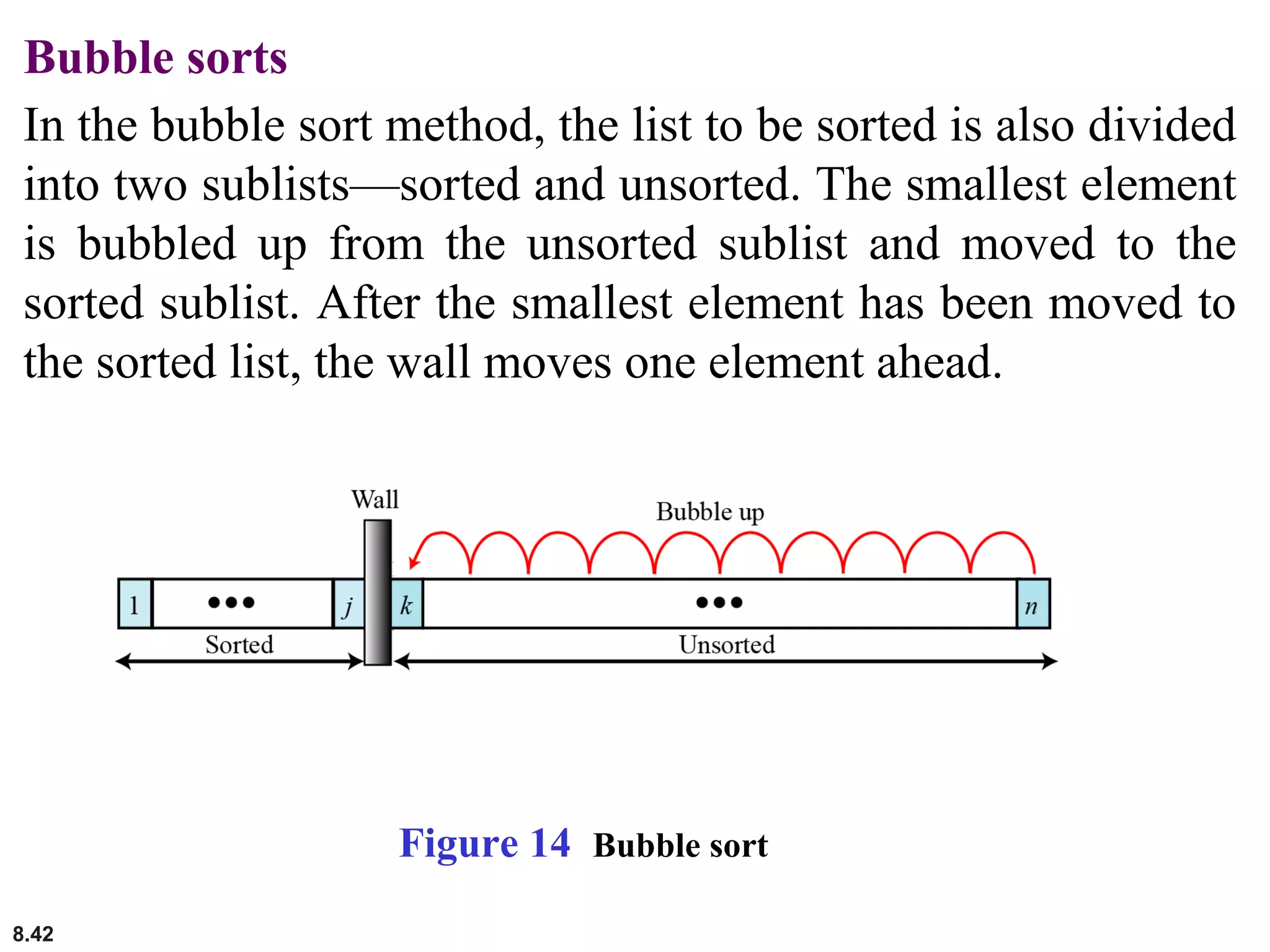
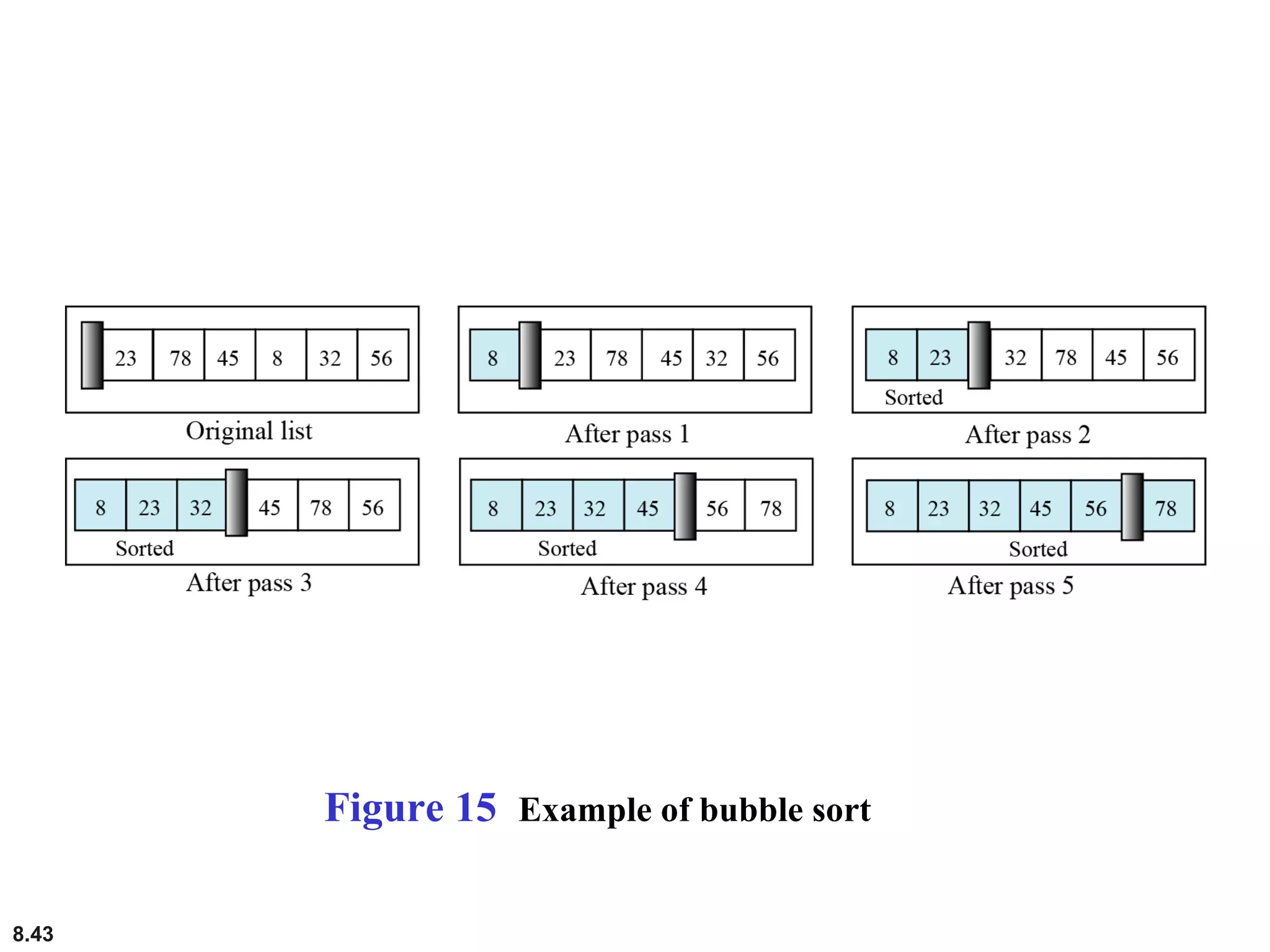
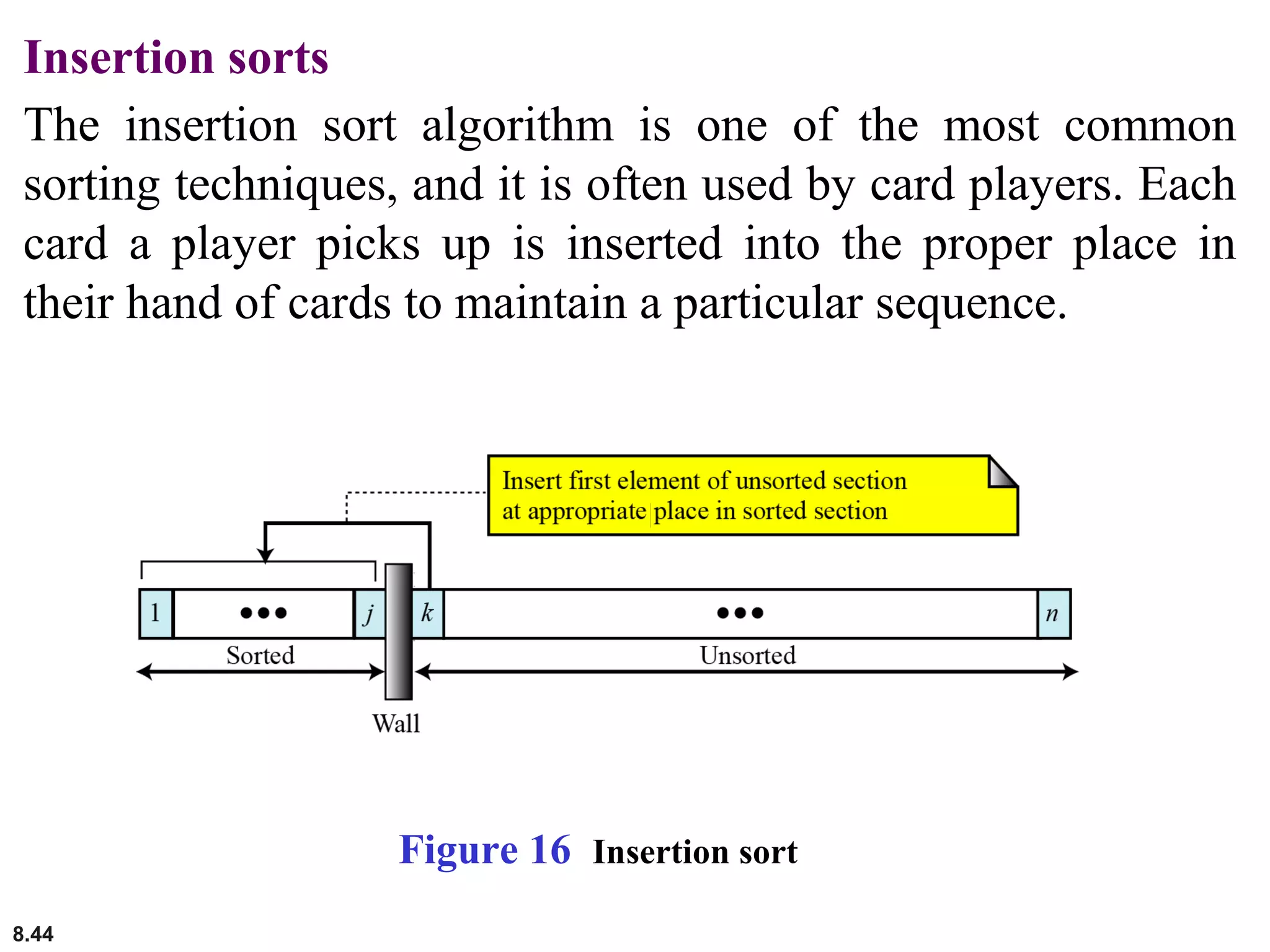
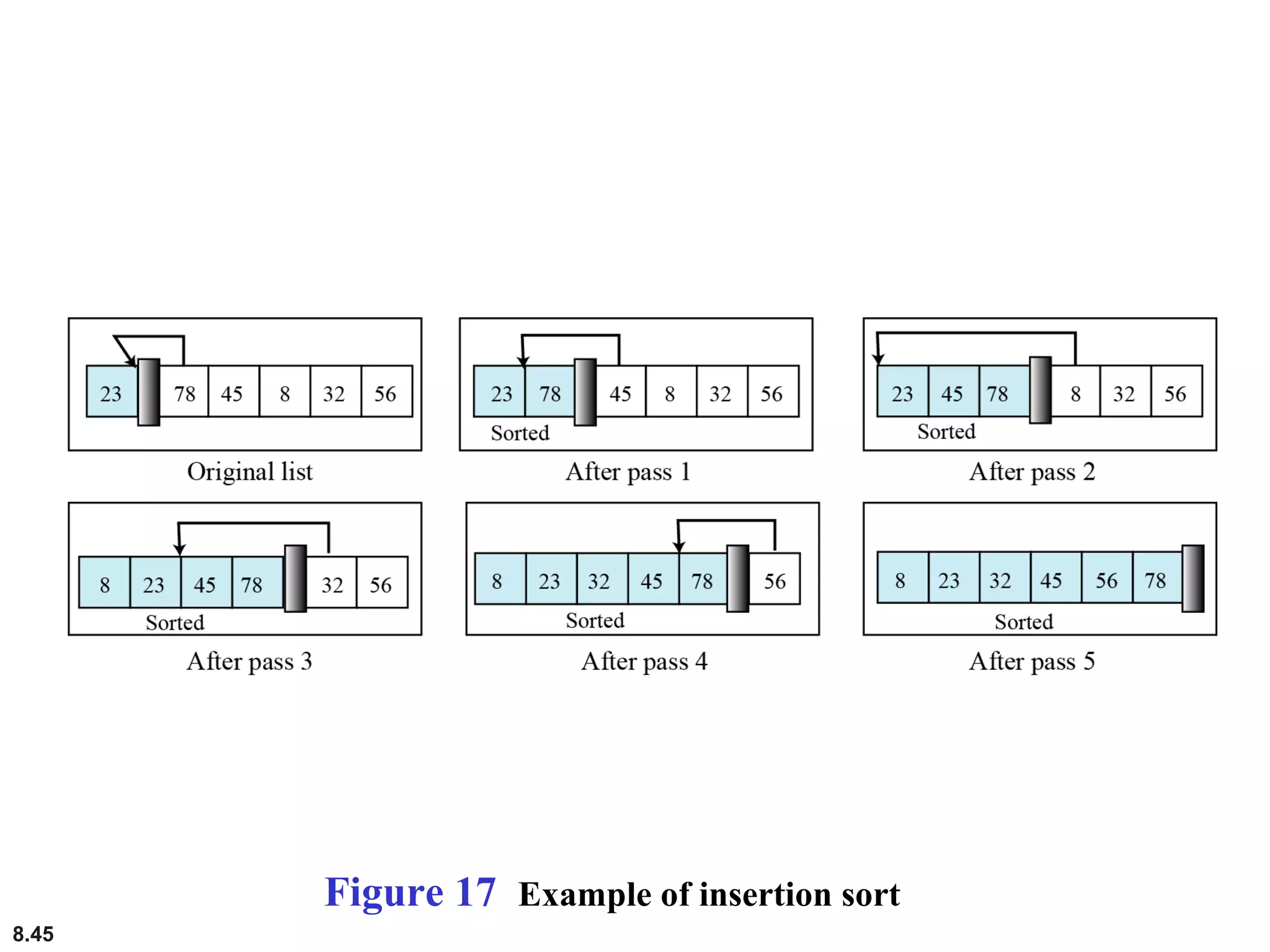
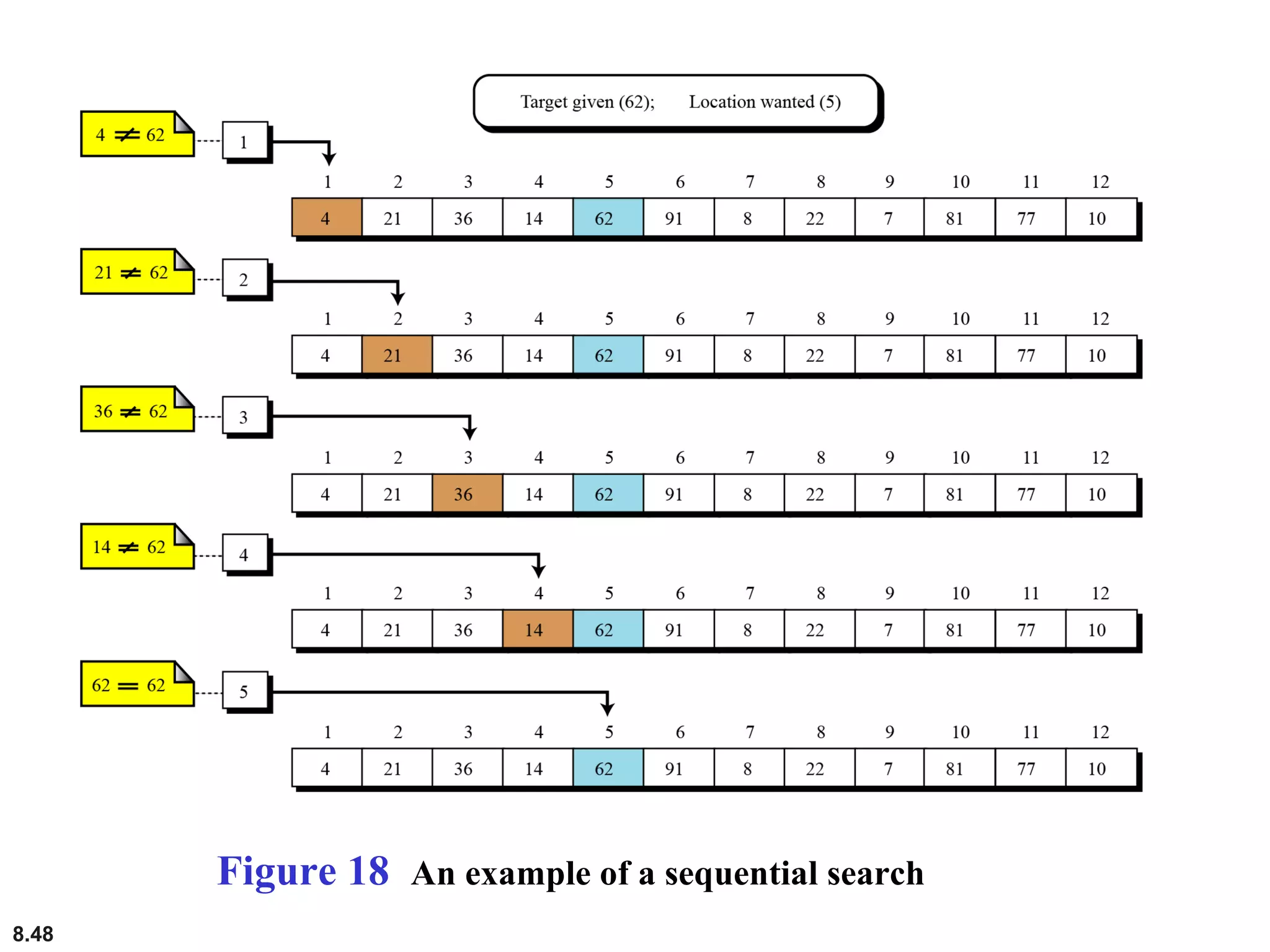
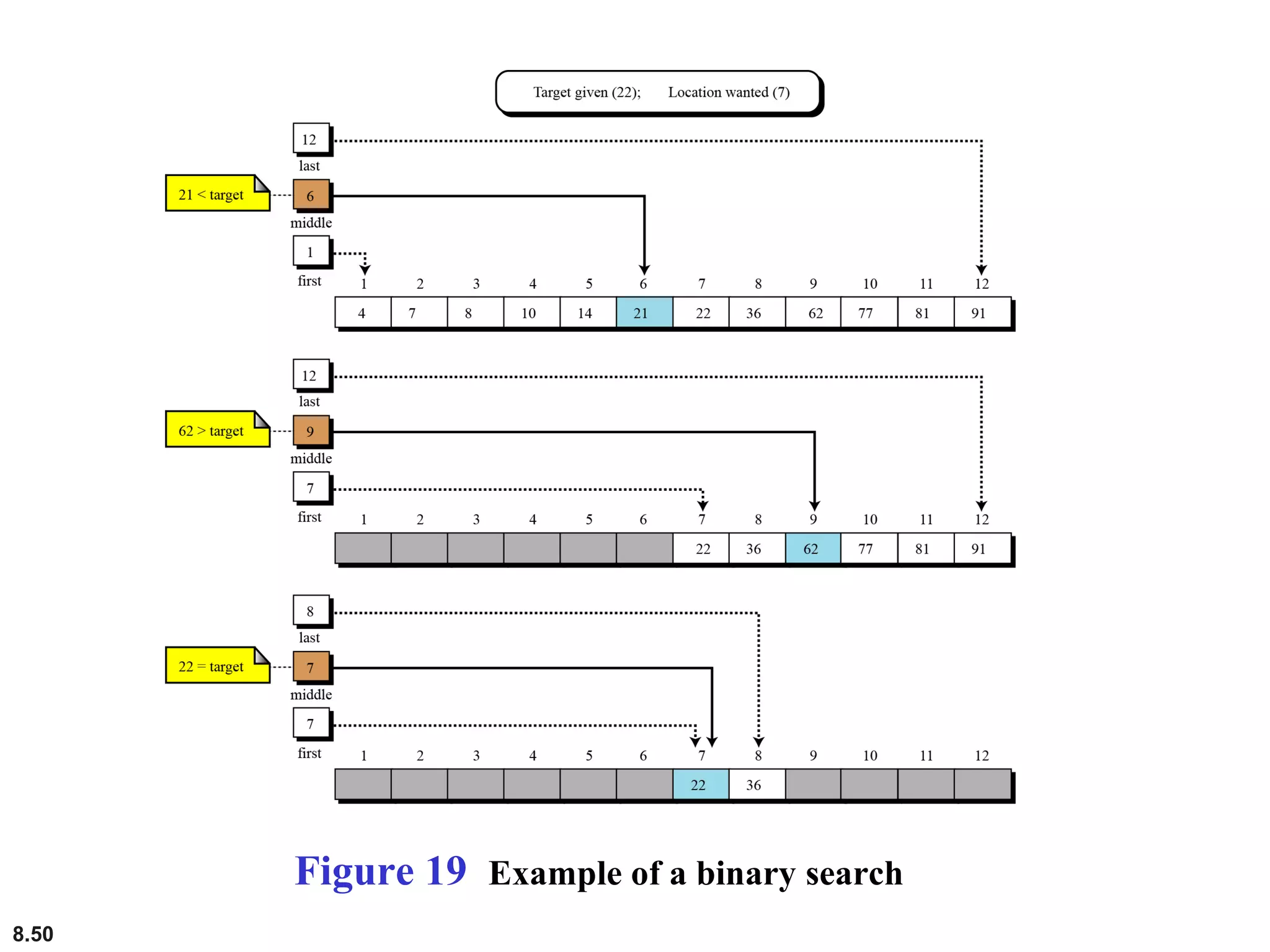
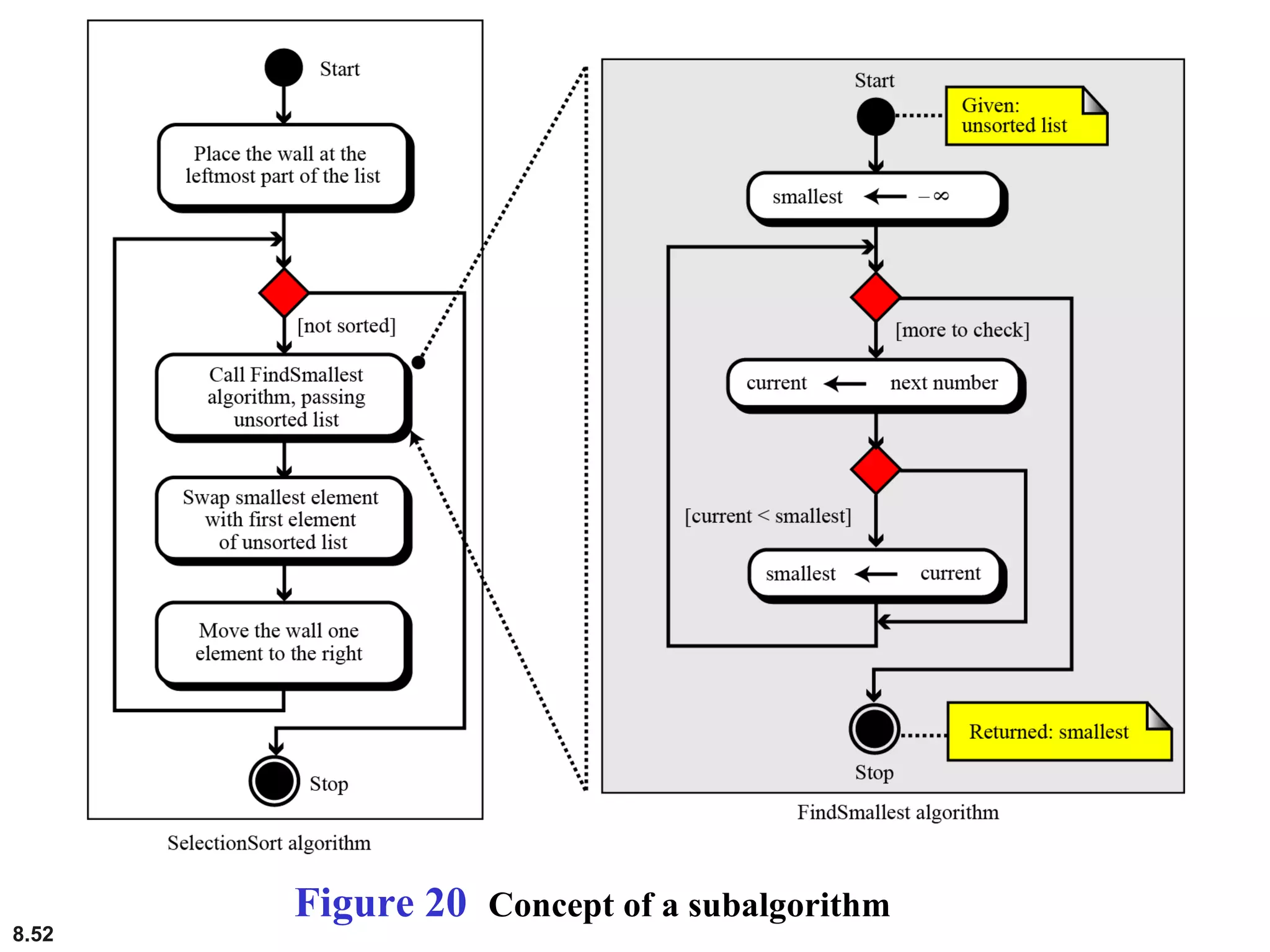
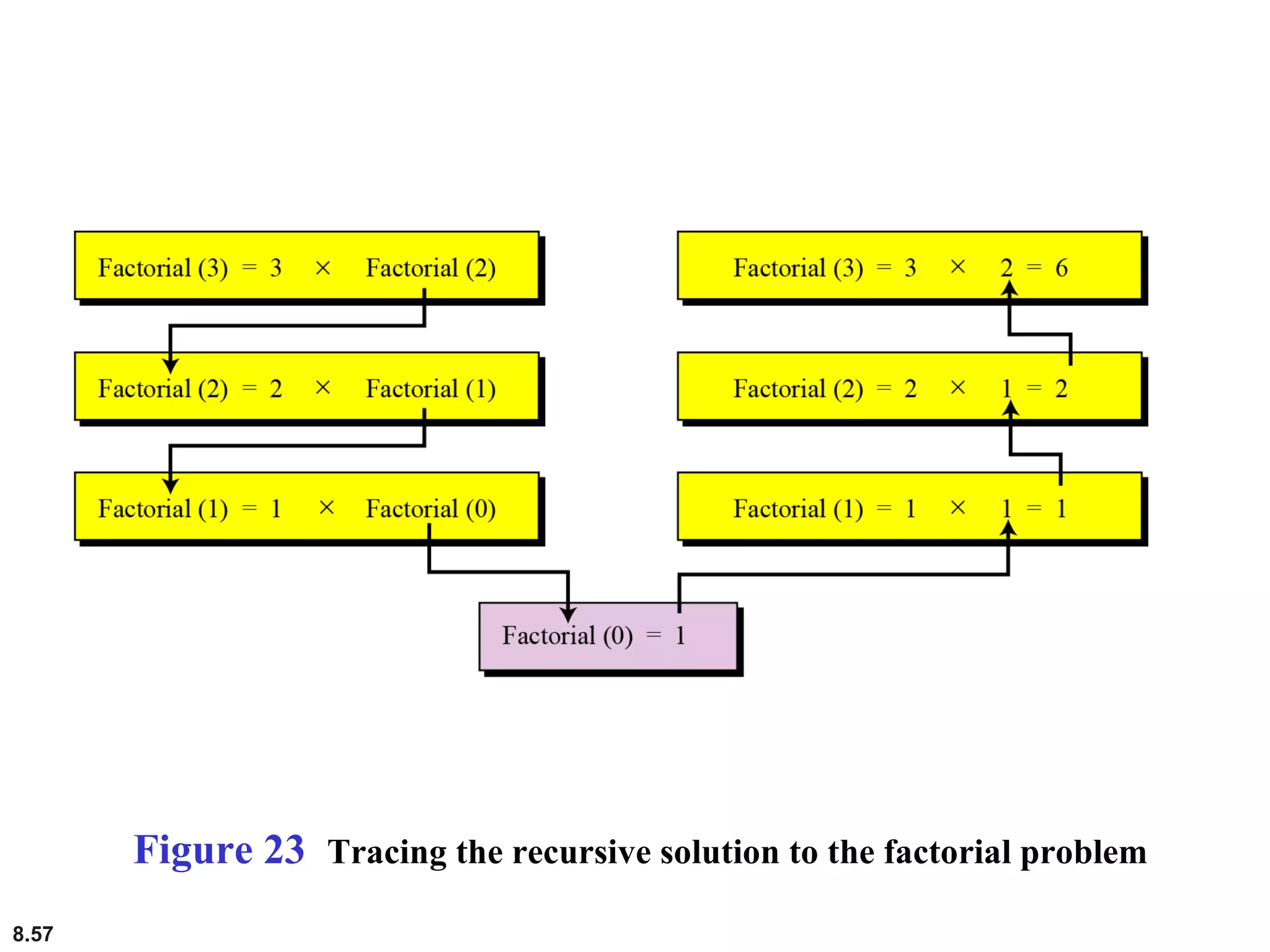
This document discusses the fundamental concepts and importance of algorithms in computer science, including their definitions, constructs, representations, and common types such as sorting and searching algorithms. It highlights key algorithmic techniques such as recursion and iteration, and offers examples of basic algorithms like summation, product, and selection sort. The document emphasizes the need for clear and structured approaches to problem-solving through algorithms.