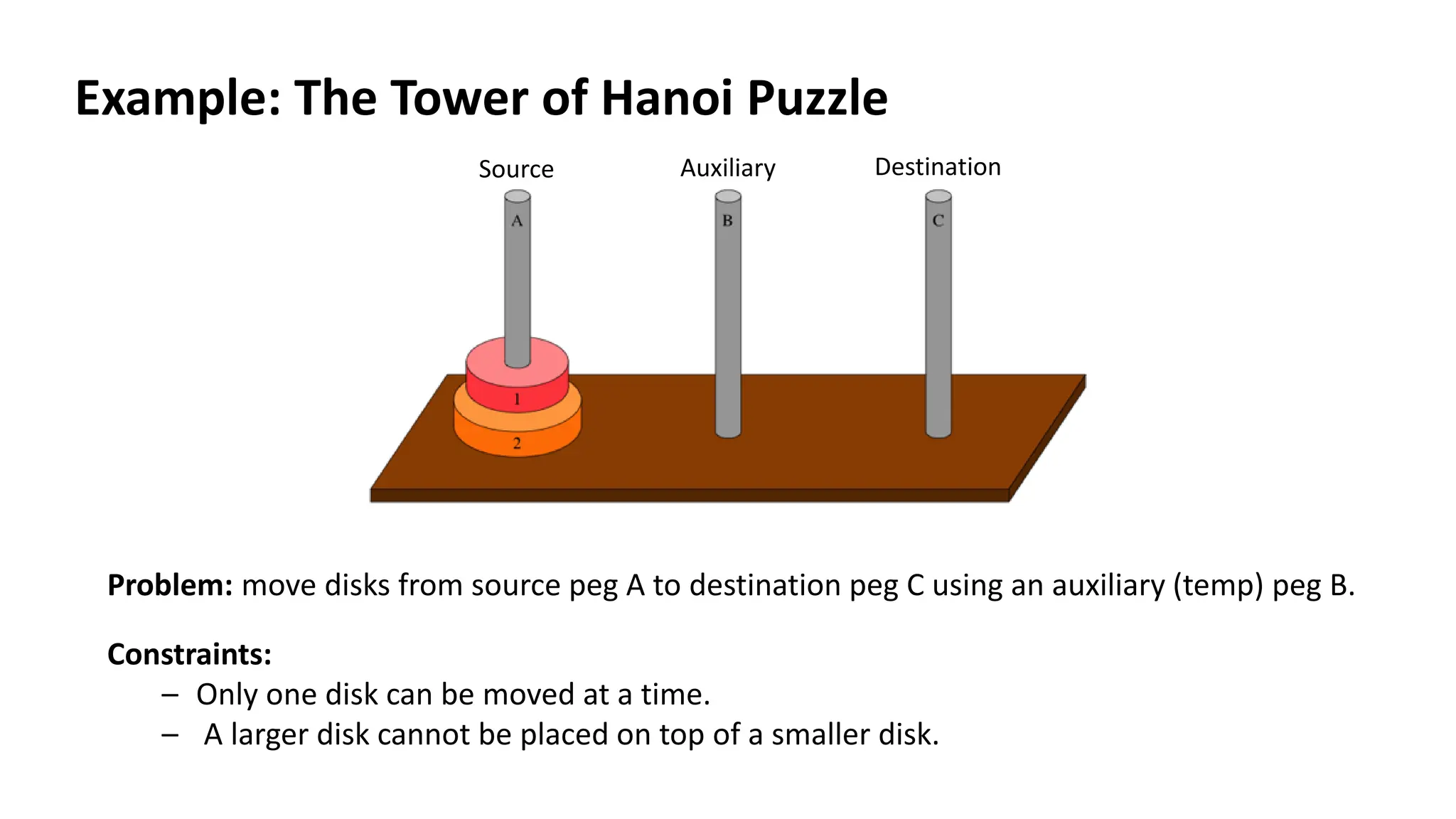
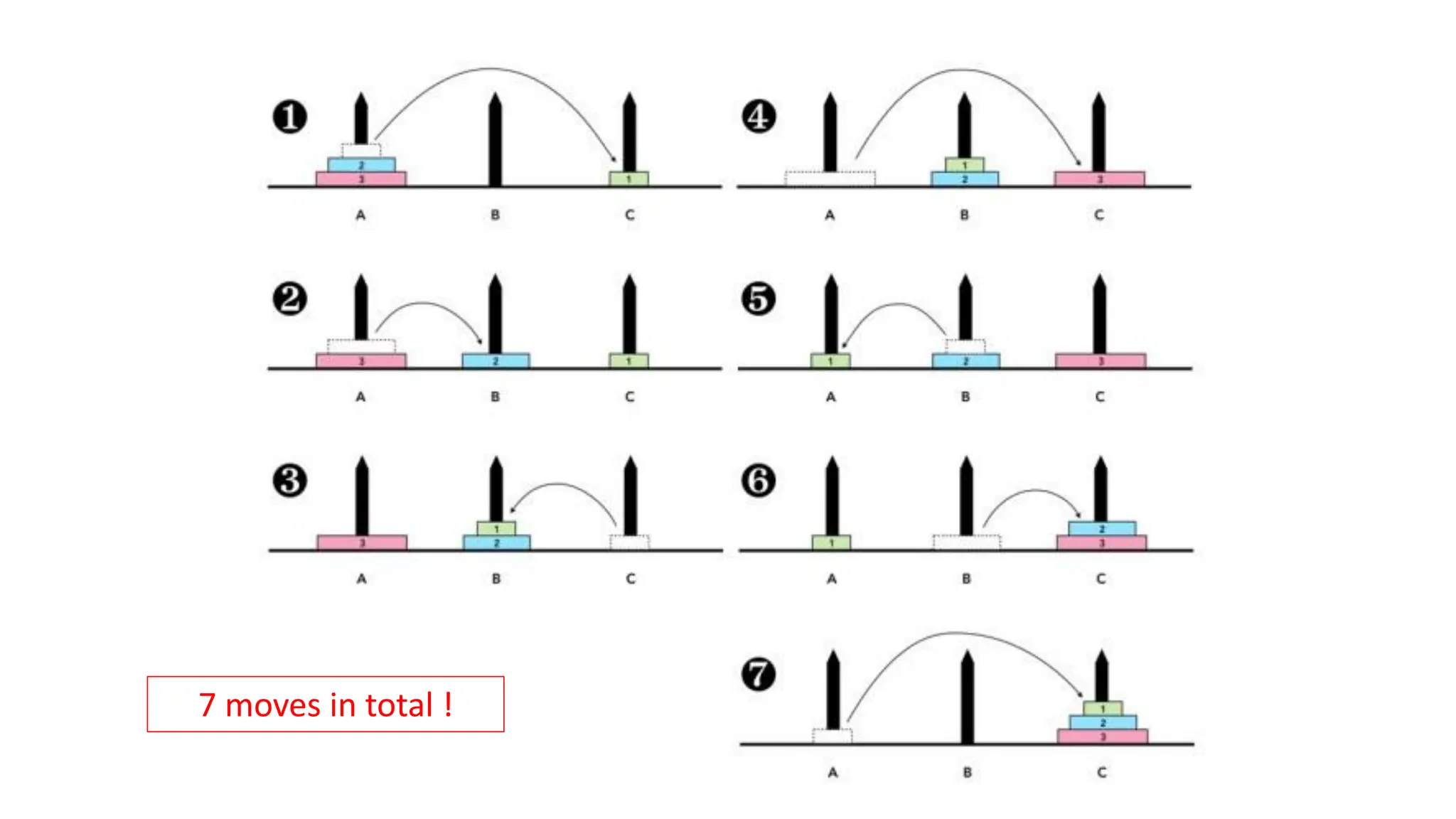
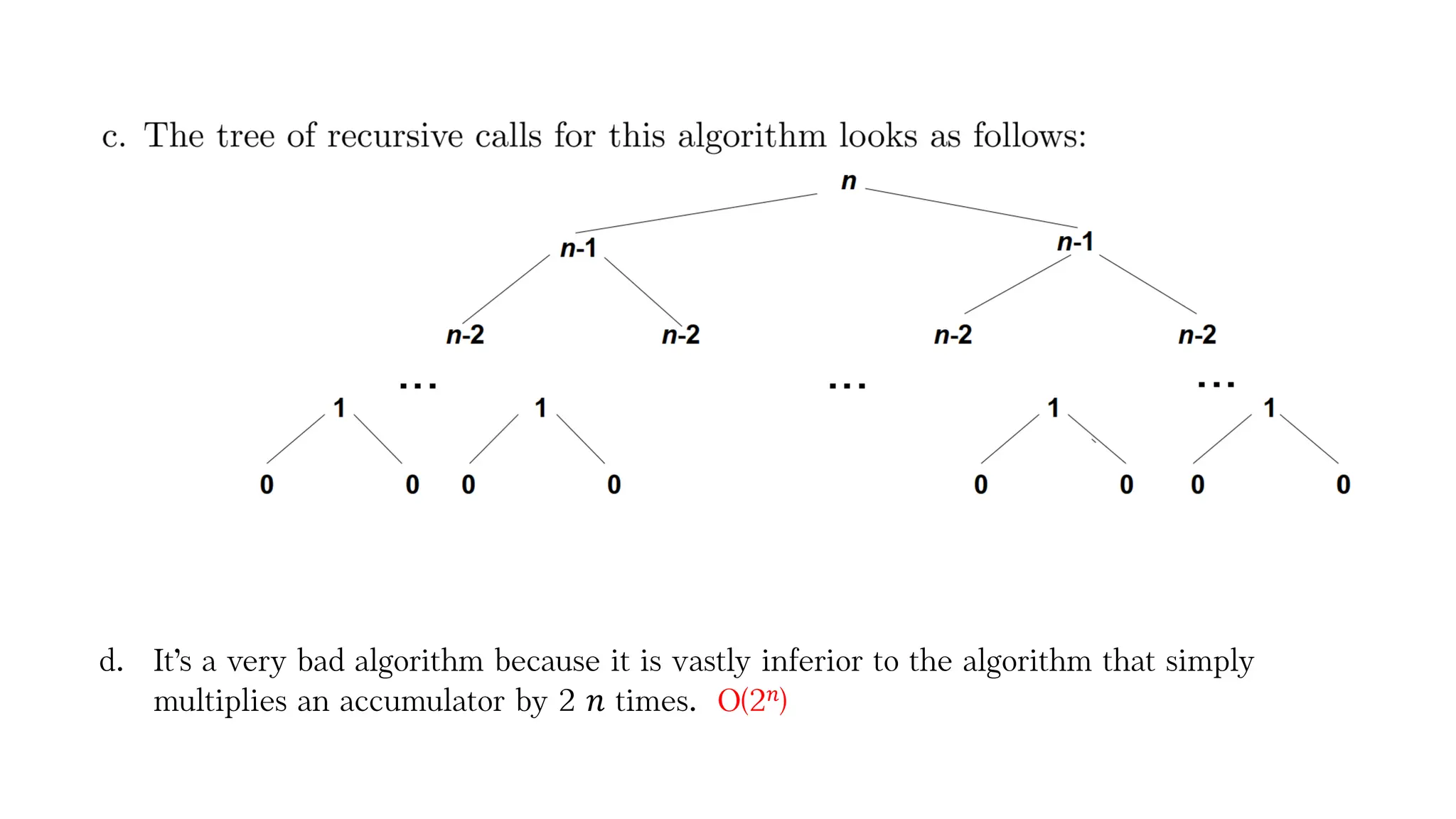
The document discusses various algorithms, particularly focusing on their recurrence relations and the number of operations they perform, such as multiplications, additions, and comparisons. It includes specific examples like the Tower of Hanoi problem and algorithms for computing powers and finding the smallest element in an array, analyzing their time complexity and operational breakdown. The document emphasizes the efficiency of different approaches and highlights the advantages of non-recursive methods.

1. Algorithms
By Mohamed Gamal
© Mohamed Gamal 2024

4. a)
Let 𝑀(𝑛) be the number of multiplications made by the algorithm.
Recurrence relation equation: 𝑀(𝑛) = 𝑀(𝑛 − 1) + 1 and 𝑀 0 = 0
• Using forward substitution:
𝑀 0 = 0
𝑀 1 = 𝑀 0 + 1 = 1
𝑀 2 = 𝑀 1 + 1 = 2
𝑀 3 = 𝑀 2 + 1 = 3
𝑀 𝑛 = 𝑛
Basic Operation

5. a) Another approach
Let 𝑀(𝑛) be the number of multiplications made by the algorithm.
Recurrence relation equation: 𝑀(𝑛) = 𝑀(𝑛 − 1) + 1 and 𝑀 0 = 0
• Using backward substitution:
𝑀 𝑛 = 𝑀 𝑛 − 1 + 1
= 𝑀 𝑛 − 2 + 1 + 1 = 𝑀 𝑛 − 2 + 2
= 𝑀 𝑛 − 3 + 1 + 2 = 𝑀 𝑛 − 3 + 3
= 𝑀 𝑛 − 4 + 1 + 3 = 𝑀 𝑛 − 4 + 4
𝑀 𝑛 = 𝑀 𝑛 − 𝑖 + 𝑖
= 𝑀 0 + 𝑛
= 𝑛
𝑛 − 𝑖 = 0
𝑖 = 𝑛

6. Example: The Tower of Hanoi Puzzle
Problem: move disks from source peg A to destination peg C using an auxiliary (temp) peg B.
Constraints:
– Only one disk can be moved at a time.
– A larger disk cannot be placed on top of a smaller disk.
Source Destination
Auxiliary

7. Try it online!

8. 7 moves in total !

9. ALGORITHM: Hanoi(n, src, dest, temp)
// Input: no. disks, source, destination, temp
// Output: Moves to solve the Tower of Hanoi problem
if n = 1 then
MOVE disk from src to dest directly
else
Hanoi(n-1, src, temp, dest) // Step 1: from src to temp
MOVE disk n from src to dest // Step 2: nth disk from src to dest
Hanoi(n-1, temp, dest, src) // Step 3: from temp to dest

10. Let 𝑀(𝑛) be the number of moves made by the algorithm.
Recurrence relation equation: 𝑀 𝑛 = 𝑀 𝑛 − 1 + 1 + 𝑀(𝑛 − 1) and 𝑀 1 = 1
= 2𝑀 𝑛 − 1 + 1
• Using forward substitution:
𝑀(1) = 1
𝑀(2) = 2𝑀(1) + 1 = 3
𝑀(3) = 2𝑀(2) + 1 = 7
𝑀(𝑛) = 2𝑛 − 1
Basic Operation

11. Let 𝑀(𝑛) be the number of moves made by the algorithm.
Recurrence relation equation: 𝑀 𝑛 = 2𝑀 𝑛 − 1 + 1 and 𝑀 1 = 1
• Using backward substitution:
𝑀(𝑛) = 2𝑀 𝑛 − 1 + 1
= 2 2𝑀 𝑛 − 2 + 1 + 1 = 4𝑀(𝑛 − 2) + 3
= 4 2𝑀 𝑛 − 3 + 1 + 3 = 8𝑀(𝑛 − 3) + 7
𝑀(𝑛) = 2𝑖 𝑀(𝑛 − 𝑖) + (2𝑖 − 1)
= 2𝑛−1
𝑀(1) + (2𝑛−1
− 1)
= 2𝑛
− 1
𝑛 − 𝑖 = 1
𝑖 = 𝑛 − 1
Basic Operation

13. Determine what this algorithm computes?
𝑄(1) = 1
𝑄(2) = 𝑄(1) + 2 ∗ 2 − 1 = 1 + 3 = 4
𝑄(3) = 𝑄(2) + 2 ∗ 3 − 1 = 4 + 5 = 9
𝑄(4) = 𝑄(3) + 2 ∗ 4 − 1 = 9 + 7 = 16
𝑄(𝑛) = 𝑛2
Then this algorithm computes 𝑛2
for each positive 𝑛.
Recurrence relation equation: 𝑄(𝑛 − 1) + 2𝑛 − 1 for 𝑛 > 1
a)

14. b)
Let 𝑀(𝑛) be the number of multiplications made by the algorithm.
Recurrence relation equation: 𝑀(𝑛) = 𝑀(𝑛 − 1) + 1 and 𝑀 1 = 0
• Using backward substitution:
𝑀 𝑛 = 𝑀 𝑛 − 1 + 1
= 𝑀 𝑛 − 2 + 1 + 1 = 𝑀 𝑛 − 2 + 2
= 𝑀 𝑛 − 3 + 1 + 2 = 𝑀 𝑛 − 3 + 3
= 𝑀 𝑛 − 4 + 1 + 3 = 𝑀 𝑛 − 4 + 4
𝑀 𝑛 = 𝑀 𝑛 − 𝑖 + 𝑖
= 𝑀 1 + (𝑛 − 1)
= (𝑛 − 1)
𝑛 − 𝑖 = 1
𝑖 = 𝑛 − 1

15. c)
Let 𝐶(𝑛) be the number of additions and subtractions made by the algorithm.
Recurrence relation equation: 𝐶(𝑛) = 𝐶(𝑛 − 1) + 2 and 𝐶 1 = 0
• Using backward substitution:
𝐶 𝑛 = 𝐶 𝑛 − 1 + 2
= 𝐶 𝑛 − 2 + 2 + 2 = 𝐶 𝑛 − 2 + 4
= 𝐶 𝑛 − 3 + 2 + 4 = 𝐶 𝑛 − 3 + 6
= 𝐶 𝑛 − 4 + 2 + 6 = 𝐶 𝑛 − 4 + 8
𝐶(𝑛) = 𝐶(𝑛 − 𝑖) + 2 ∗ 𝑖
= 𝐶 1 + 2 ∗ 𝑛 − 1
= 2(𝑛 − 1)
𝑛 − 𝑖 = 1
𝑖 = 𝑛 − 1

17. a)
Let 𝑀(𝑛) be the number of multiplications made by the algorithm.
Recurrence relation equation: 𝑀(𝑛) = 𝑀(𝑛 − 1) + 2 and 𝑀 1 = 0
• Using forward substitution:
𝑀(1) = 0
𝑀(2) = 𝑀(1) + 2 = 2
𝑀(3) = 𝑀(2) + 2 = 4
𝑀(4) = 𝑀(3) + 2 = 6
𝑀(5) = 𝑀(4) + 2 = 8
𝑀 𝑛 = 2 𝑛 − 1
Basic Operation

18. a) Another approach
Let 𝑀(𝑛) be the number of multiplications made by the algorithm.
Recurrence relation equation: 𝑀(𝑛) = 𝑀(𝑛 − 1) + 2 and 𝑀 1 = 0
• Using backward substitution:
𝑀(𝑛) = 𝑀(𝑛 − 1) + 2
= [ 𝑀(𝑛 − 2) + 2 ] + 2 = 𝑀(𝑛 − 2) + 4
= [ 𝑀(𝑛 − 3) + 2 ] + 4 = 𝑀(𝑛 − 3) + 6
= [ 𝑀(𝑛 − 4) + 2 ] + 6 = 𝑀(𝑛 − 4) + 8
𝑀(𝑛) = 𝑀 𝑛 − 𝑖 + 2𝑖
= 𝑀 1 + 2(𝑛 − 1)
= 2 𝑛 − 1
Basic Operation
𝑛 − 𝑖 = 1
𝑖 = 𝑛 − 1

19. ALGORITHM: S(n)
// Input: A positive integer n
// Output: The sum of the first n cubes
S ← 1
for i ← 2 to n do
S ← S + i * i * i
return S
The number of multiplications made by this algorithm will be
෍
𝑖=2
𝑛
2 =
𝑛 − 2 + 1
2
× (2 + 2) = 2(𝑛 − 1)
This is exactly the same number as in the recursive version, but the no recursive version
doesn't carry the time and space overhead associated with the recursion's stack.
b) Comparing with the non-recursive algorithm

20. Question 1:
Assignments

21. Question 2:

22. ThankYou!

24. Question 1

25. Answers

26. b)
Let 𝐴(𝑛) be the number of additions made by the algorithm.
Recurrence relation equation: 𝐴 𝑛 = 𝐴 𝑛 − 1 + 𝐴(𝑛 − 1) + 1 and 𝐴 0 = 0
= 2𝐴 𝑛 − 1 + 1
• Using forward substitution:
𝐴(0) = 0
𝐴(1) = 2𝐴(0) + 1 = 1
𝐴(2) = 2𝐴(1) + 1 = 3
𝐴(3) = 2𝐴(2) + 1 = 7
𝐴(4) = 2𝐴(3) + 1 = 15
𝐴 𝑛 = 2𝑛 − 1
Basic Operation

27. b) Another approach
Let 𝐴(𝑛) be the number of additions made by the algorithm.
Recurrence relation equation: 𝐴(𝑛) = 2𝐴(𝑛 − 1) + 1 and 𝐴 0 = 0
• Using backward substitution:
𝐴(𝑛) = 2𝐴(𝑛 − 1) + 1
= 2[ 2𝐴(𝑛 − 2) + 1 ] + 1 = 4𝐴(𝑛 − 2) + 3
= 4[ 2𝐴(𝑛 − 3) + 1 ] + 3 = 8𝐴(𝑛 − 3) + 7
= 8[ 2𝐴(𝑛 − 4) + 1 ] + 7 = 16𝐴(𝑛 − 4) + 15
𝐴 𝑛 = 2𝑖𝐴 𝑛 − 𝑖 + (2𝑖 − 1)
= 2𝑛 𝑀 0 + (2𝑛 − 1)
= 2𝑛 − 1
Basic Operation
𝑛 − 𝑖 = 0
𝑖 = 𝑛

28. d. It’s a very bad algorithm because it is vastly inferior to the algorithm that simply
multiplies an accumulator by 2 𝑛 times. O(2𝑛)

29. Question 2

30. a) The algorithm computes the value of the smallest element in a given array.
Let A = [9, 5, 8, 2]
▪ n = 4 ≠ 1
▪ Call Riddle([9, 5, 8]) (subarray A[0..2]):
▪ For Riddle([9, 5, 8]):
▪ n = 3 ≠ 1
▪ Call Riddle([9, 5]) (subarray A[0..1]):
▪ For Riddle([9, 5]):
▪ n = 2 ≠ 1
▪ Call Riddle([9]) (subarray A[0..0]):
▪ n = 1, so it returns 9.
▪ Compare temp = 9 with A[1] = 5:
▪ 9 > 5, so return 5.
▪ Riddle([9, 5]) returns 5.
▪ Compare temp = 5 with A[2] = 8:
▪ 5 <= 8, so return 5.
▪ Riddle([9, 5, 8]) returns 5.
▪ Compare temp = 5 with A[3] = 2:
▪ 5 > 2, so return 2.

31. b)
Let 𝐶(𝑛) be the number of the number of key comparisons made by the algorithm.
Recurrence relation equation: 𝐶(𝑛) = 𝐶(𝑛 − 1) + 1 and 𝐶 1 = 0
• Using backward substitution:
𝐶 𝑛 = 𝐶(𝑛 − 1) + 1
= [ 𝐶(𝑛 − 2) + 1 ] + 1 = 𝐶(𝑛 − 2) + 2
= [ 𝐶(𝑛 − 3) + 1 ] + 2 = 𝐶(𝑛 − 3) + 3
= [ 𝐶(𝑛 − 4) + 1 ] + 3 = 𝐶(𝑛 − 4) + 4
𝐶 𝑛 = 𝐶 𝑛 − 𝑖 + 𝑖
= 𝐶 1 + (𝑛 − 1)
= 𝑛 − 1
Basic Operation
𝑛 − 𝑖 = 1
𝑖 = 𝑛 − 1