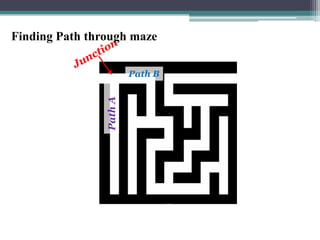
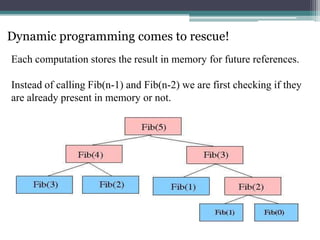
This document discusses various algorithm paradigms, including brute force, divide and conquer, backtracking, greedy, and dynamic programming. It provides examples of problems that each paradigm can help solve. The brute force paradigm tries all possible solutions, often being the most expensive approach. Divide and conquer breaks problems into identical subproblems, solves them recursively, and combines the solutions. Backtracking uses depth-first search to systematically try and eliminate possibilities. Greedy algorithms make locally optimal choices at each step to find a global optimal solution. Dynamic programming solves problems with overlapping subproblems by storing and looking up past solutions instead of recomputing them.

1. Algorithm Paradigms
By
G Suresh Babu

2. Algorithm
An algorithm is a step-by-step procedure for
solving a problem.
Paradigm
“Pattern of thought” which governs scientific
apprehension during a certain period of time

3. Paradigms for Algorithm Design
To aid in designing algorithms for new problems, we
create a taxonomy of high level patterns or
paradigms, for the purpose of structuring a new
algorithm along the lines of one of these paradigms.
A paradigm can be viewed as a very high level
algorithm for solving a class of problems

4. Various algorithm Paradigms
Brute force paradigm
Divide and conquer paradigm
Backtracking paradigm
Greedy paradigm
Dynamic programming paradigm

5. Brute force paradigm
Brute force is one of the easiest and straight forward
approach to solve a problem
Based on trying all possible solutions
It is useful for solving small–size instances of a
problem
Generally most expensive approach
Examples: Sequential search, factors of number

6. Divide and conquer paradigm
 Based on dividing problem into sub problems
Approach
1. Divide problem into smaller sub problems
 Sub problems must be of same type
 Sub problems do not need to overlap
2. Solve each sub problem recursively
3. Combine solutions to solve original problem
Examples : Merge Sort, Quick Sort.

7. Backtracking paradigm
 Backtracking is a technique used to solve problems
with a large search space, by systematically trying
and eliminating possibilities
Based on depth-first recursive search
Examples : Find path through maze, eight queens
problem

8. Finding Path through maze
Path A
Path B

9. Eight Queens Problem
Find an arrangement of 8 queens
on a single chess board such that
no two queens are attacking one
another.
1) Place a queen on the first
available square in row 1.
2) Move onto the next row,
placing a queen on the first
available square there (that
doesn't conflict with the
previously placed queens).

10. Greedy paradigm
Optimal solution :A solution which minimizes or
maximizes objective function is called optimal solution
(i.e. BEST solution)
This technique suggest devising an algorithm in no of
steps, each stage depends on a particular input which
gives “optimal solution”.
Examples : 0/1 knapsack, kruskals & prims, counting
money, Dijkstra’s shortest path algorithm

11. Counting money
Suppose you want to count certain amount of money, using
the fewest possible bills and coins
A greedy algorithm to do this would be:
1. At each step, take the largest possible bill or coin that does
not overshoot
Example: To make 17Rs from 1,5,10 rupee denominations
a)add 10 rupee note
b)add 5 rupee note
c)add two 1 rupee notes

12. Dynamic programming paradigm
It is also an optimization technique.
Based on remembering past results
Approach
a) Divide problem into smaller sub problems
Sub problems must be of same type
Sub problems must overlap
b)Solve each sub problem recursively
May simply look up solution
c)Combine solutions into to solve original problem
Store solution to problem
Examples: All pairs shortest path, Fibonacci series

13. Fibonacci series
Fibonacci numbers
– Fibonacci(0) = 1
– Fibonacci(1) = 1
– Fibonacci(n) = Fibonacci(n-1) + Fibonacci(n-2)
Recursive algorithm to calculate Fibonacci(n)
– If n is 0 or 1, return 1
– Else compute Fibonacci(n-1) and Fibonacci(n-2)
– Return their sum

14. Dynamic programming comes to rescue!
Each computation stores the result in memory for future references.
Instead of calling Fib(n-1) and Fib(n-2) we are first checking if they
are already present in memory or not.

15. Summary
Wide range of strategies
Choice depends on
 Properties of problem
 Expected problem size
 Available resources
Any queries ???

16. Thank you