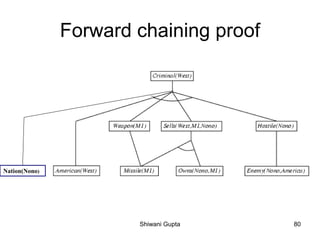
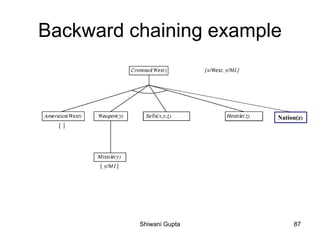
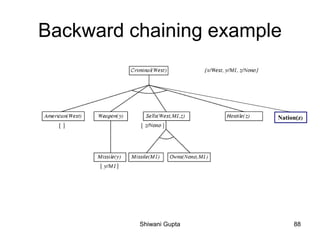
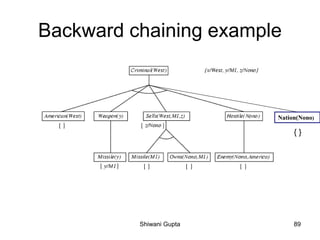
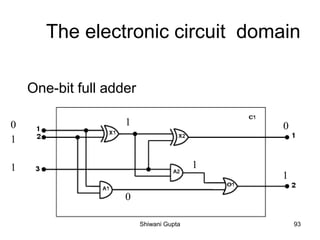
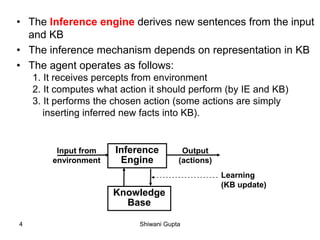
The document discusses knowledge-based agents and how they use inference to derive new representations of the world from their knowledge base in order to determine what actions to take. It provides the example of an agent exploring a cave, or "Wumpus world", where the goal is to locate gold and exit without being killed by the Wumpus monster or falling into pits. The agent uses its percepts and knowledge base along with inference rules to deduce its next action at each step.

1. Module 4
KNOWLEDGE
AND
REASONING

2. Knowledge based agent
• We design agents that can form representations of the
world
• Agents that use a process of inference to derive new
representations about the world
• and agents that use these new representations to
deduce what to do
• A knowledge-based agent needs to know many
things:
– the current state of the world
– how to infer unseen properties of the world from percepts
– how the world evolves over time
– what it wants to achieve
– what its own actions do in various circumstances
Shiwani Gupta 2

3. Knowledge Base
(set of representations of facts about the world)
• The knowledge level or epistemological level is the most abstract;
we can describe the agent by saying what it knows. For example, an
automated taxi might be said to know that the Golden Gate Bridge
links San Francisco and Marin County.
• The logical level is the level at which the knowledge is encoded into
sentences. For example, the taxi might be described as having the
logical sentence Links(GGBridge, SF, Marin) in its knowledge base.
• The implementation level is the level that runs on the agent
architecture. It is the level at which there are physical representations
of the sentences at the logical level. A sentence such as
Links(GGBridge, SF, Marin) could be represented in the KB by the
string "Links (GGBridge, SF, Marin)" contained in a list of strings; or
by a "1" entry in a three-dimensional table indexed by road links and
location pairs; or by a complex set of pointers connecting machine
addresses corresponding to the individual symbols. The choice of
implementation is very important to the efficient performance of the
agent, but it is irrelevant to the logical level and the knowledge level.
Shiwani Gupta 3

4. 4
• The Inference engine derives new sentences from the input
and KB
• The inference mechanism depends on representation in KB
• The agent operates as follows:
1. It receives percepts from environment
2. It computes what action it should perform (by IE and KB)
3. It performs the chosen action (some actions are simply
inserting inferred new facts into KB).
Knowledge
Base
Inference
Engine
Input from
environment
Output
(actions)
Learning
(KB update)
Shiwani Gupta

5. Example – Knowledge Based Agent
• A classical AI problem
• An early computer game
• An agent had to explore a cave made of series of
interconnected rooms
• In one room, there was a Wumpus who would kill agent if it
entered the room
• Some rooms have pits – agent would die if it entered it
• Agent had 1 arrow to kill Wumpus
• Goal – Locate gold and return to start without getting killed.
Shiwani Gupta 5

6. Shiwani Gupta 6

7. The Wumpus World
environment
• The Wumpus computer game
• The agent explores a cave consisting of rooms connected by
passageways.
• Lurking somewhere in the cave is the Wumpus, a beast that
eats any agent that enters its room.
• Some rooms contain bottomless pits that trap any agent that
wanders into the room.
• It is safe to enter a square with dead Wumpus.
• Occasionally, there is a heap of gold in a room.
• The goal is:
– to collect the gold and
– exit the world (climb out of cave)
– without being eaten Shiwani Gupta 7

8. Wumpus World PEAS description
• Performance measure:
– gold +1000, death -10000
– -1 per step, -10 for using the arrow
• Environment:
– Squares adjacent to wumpus are smelly
– Squares adjacent to pit are breezy
– Glitter iff gold is in the same square
– Shooting kills wumpus if you are facing it,
it screams
– Shooting uses up the only arrow
– Grabbing picks up gold if in same square
– Releasing drops the gold in same square
– You bump if you walk into a wall
• Actuators: Left turn, Right turn, Forward, Grab, Climb, Shoot
• Sensors: Stench, Breeze, Glitter, Bump, Scream
Shiwani Gupta 8

9. Wumpus world characterization
• Fully Observable No – only local perception
• Deterministic Yes – outcomes exactly specified
• Episodic No – since no need to think ahead
• Static Yes – Wumpus and Pits do not move
• Discrete Yes
• Single-agent Yes – Wumpus is essentially a
natural feature
Shiwani Gupta 9

10. The first step taken by the agent in the wumpus world,
(a)The initial situation, after percept [None, None, None, None, None].
(b)After one move, with percept [None, Breeze, None, None, None].
[ stench,  breeze,  glitter,  bump,  scream] [1,1]
[stench,  breeze,  glitter,  bump,  scream] [1,2]
[ stench, breeze,  glitter,  bump,  scream] [2,1] → Safe cell
Shiwani Gupta 10

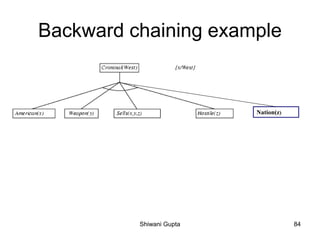
11. Two later stages in the progress of the agent,
(a) After the third move, with percept [Stench, None, None, None, None].
(b) After the fifth move, with percept [Stench, Breeze, Glitter, None, None].
Shiwani Gupta 11

12. Propositional logic: Syntax
(limited expressiveness)
• Propositional logic is the simplest logic – illustrates basic ideas
• The proposition symbols P1, P2 etc are sentences
– If S is a sentence, S is a sentence (negation)
– If S1 and S2 are sentences, S1  S2 is a sentence
(conjunction)
– If S1 and S2 are sentences, S1  S2 is a sentence
(disjunction)
– If S1 and S2 are sentences, S1  S2 is a sentence
(implication)
– If S1 and S2 are sentences, S1  S2 is a sentence
(biconditional)
Shiwani Gupta 12

13. Symbols of propositional logic
• Logical constants TRUE and FALSE are sentences
• Proposition symbols P and Q are sentences
• A, V, , , are logical connectives
• parenthesis ( )
Shiwani Gupta 13

14. Ambiguity
• P A Q V R
(P A Q) V R
P A (Q V R)
• Order of precedence (highest to lowest)
Shiwani Gupta 14

15. Propositional logic: Semantics
Each model specifies true/false for each proposition symbol
E.g. P1,2 P2,2 P3,1
false true false
With these symbols, 8 possible models, can be enumerated automatically.
Rules for evaluating truth with respect to a model m:
S is true iff S is false
S1  S2 is true iff S1 is true and S2 is true
S1  S2 is true iff S1is true or S2 is true
S1  S2 is true iff S1 is false or S2 is true
i.e., is false iff S1 is true and S2 is false
S1  S2 is true iff S1S2 is true and S2S1 is true
Simple recursive process evaluates an arbitrary sentence, e.g.,
P1,2  (P2,2  P3,1) = true  (true  false) = true  true = true
Shiwani Gupta 15

16. Truth tables for connectives
If P then Q
If same then true else false
If P then Q and If Q then P
Shiwani Gupta 16

17. Shiwani Gupta 17

18. Logical equivalence
• Two sentences are logically equivalent iff true in same models:
α ≡ ß iff α╞ β and β╞ α
Shiwani Gupta 18

19. Inference Rules
Shiwani Gupta 19

20. DNF (SOP) to CNF (POS)
for resolution refutation
Disjunctive Normal Form
(P  Q  R) V (X   Y  Z)
Conjunctive Normal Form
( P V X)  (P V  Y)  (P V Z)  (…..)
Every sentence of propositional logic is logically
equivalent to a conjunction of disjuncts of literals
Shiwani Gupta 20

21. Conversion to CNF
• Eliminate α ß to (α  ß )  (ß  α )
• Eliminate α  ß to  α V ß
• CNF requires  to appear only with literals
For this apply
( α) ≡ α (double-negative elimination)
 (α  ß) ≡  α V  ß (de Morgan)
 (α V ß) ≡  α   ß (de Morgan)
• Now we have a sentence with nested  and V
operators applied to literals. Apply distributivity law
distributing V over 
Shiwani Gupta 21

22. Resolution Inference Rule for CNF
( )
( )
( )
A B C
A
B C
 

− − − − − − − − − − − −
 
“If A or B or C is true, but not A, then B or C
must be true.”
( )
( )
( )
A B C
A D E
B C D E
 
  
− − − − − − − − − − −
   
“If A is false then B or C must be true,
or if A is true then D or E must be true,
hence since A is either true or false, B or
C or D or E must be true.”
( )
( )
( )
A B
A B
B B B

 
− − − − − − − −
  
Simplification
Shiwani Gupta 22

23. Q ~Q v P ~P v ~Q v R premises
P
~Q v R
R theorem
Proof by resolution
Shiwani Gupta 23

24. Horn Clauses
• Resolution in general can be exponential in space and time.
• If we can reduce all clauses to “Horn clauses” resolution is linear in
space and time
A clause with at most 1 positive literal. e.g.
• Every Horn clause can be rewritten as an implication with a
conjunction of positive literals in the premises and a single positive
literal as a conclusion.
e.g.
A B C   
B C A 
Shiwani Gupta 24

25. Wumpus world in propositional logic
• Facts are propositions:
– e.g., W44 “Wumpus is at square (4,4)
– 96 propositions (16 each for wumpus, stench,
pit, breeze, gold, glitter) to represent a
particular cave
• General knowledge in sentences:
– e.g., W44  (S44 S43 S34) “if the wumpus is
at (4,4), there is stench at (4,4), (4,3) and
(3,4)”
– “many” sentences
Shiwani Gupta 25

26. • Some Atomic Propositions
S12 = There is a stench in cell (1,2)
B34 = There is a breeze in cell (3,4)
W22 = The Wumpus is in cell (2,2)
V11 = We have visited cell (1,1)
OK11 = Cell (1,1) is safe.
etc
• Some rules
(R1) ~S11 => ~W11 ^ ~W12 ^ ~W21
(R2) ~S21 => ~W11 ^ ~W21 ^ ~W22 ^ ~W31
(R3) ~S12 => ~W11 ^ ~W12 ^ ~W22 ^ ~W13
(R4) S12 => W13 v W12 v W22 v W11
etc
Wumpus world in propositional logic
Shiwani Gupta 26

27. Shiwani Gupta 27

28. Problems with propositional agent
• There are too many propositions to handle
eg. The simple rule “don’t go forward if wumpus
is in front of you” can be stated by set of 64
rules in propositional logic
• What if the world changes over time
Shiwani Gupta 28

29. Question bank
1. Represent each of these sentences in propositional logic.
a. If I take History, I cannot take Economics.
b. I must take either Japanese or Italian but not both.
c. I must take at least two of cs520, cs552, and cs564.
2. Use truth tables to show the following sentences are valid, and thus that the
equivalences hold:
P ^ (Q ^ R) <=> (P ^ Q) ^ R Associativity of conjunction
P / (Q / R) <=> (P / Q) / R Associativity of disjunction
P ^ Q <=> Q ^ P Commutativity of conjunction
P / Q <=> Q / P Commutativity of disjunction
P ^ (Q / R) <=> (P ^ Q) / ( P ^ R) Distributivity of ^ over /
P / (Q ^ R) <=> (P / Q) ^ ( P / R) Distributivity of / over ^
~(P ^ Q) <=> ~Q / ~P de Morgan’s Law
~(P / Q) <=> ~Q ^ ~P de Morgan’s Law
P => Q <=> ~Q => ~P Contraposition
~ ~P <=> P Double negation
P => Q <=> ~P / Q
P <=> Q <=> (P => Q) ^ (Q => P)
P <=> Q <=> (P ^ Q) / (~Q ^ ~P)
P ^ ~P <=> False
P / ~P <=> True
Shiwani Gupta 29

30. Question bank
• Explain the steps involved in converting
the propositional logic statement into CNF
with a suitable example
Shiwani Gupta 30

31. Pros and cons of propositional logic
☺ Propositional logic is declarative: pieces of syntax
correspond to facts
☺ Propositional logic allows partial/disjunctive/negated
information (unlike most data structures and
databases)
☺Propositional logic is compositional: meaning of B1,1 
P1,2 is derived from meaning of B1,1 and of P1,2
☺ Propositional logic is context-independent (unlike
natural language, where meaning depends on
context)
Propositional calculus requires explicit enumeration
All elephants are gray: elephant1-is-gray^elephant1-is-gray^….
logic has very limited expressive power (unlike natural
language) Shiwani Gupta 31

32. First-order predicate logic
• Propositional logic assumes the world contains
facts
• First-order logic (like natural language)
assumes the world contains
– Objects: people, houses, numbers, colors, baseball
games, wars, …
– Relations: brother of, bigger than, inside, part of,
has color, occurred after, owns…
– Properties: red, round, bogus, prime, multistoried...
– Functions: father of, best friend, one more than,
plus, …
Shiwani Gupta 32

33. Examples
• "One plus two equals three"
Objects: one, two, three, one plus two
Relation: equals
Function: plus. (One plus two is a name for the object that is
obtained by applying the function plus to the objects one and
two. Three is another name for this object.)
• "Squares neighboring the wumpus are smelly."
Objects: wumpus, square
Property: smelly
Relation: neighboring.
• "Evil King John ruled England in 1200."
Objects: John, England, 1200
Relation: ruled
Properties: evil, king.
Shiwani Gupta 33

34. Syntax of FOL: Basic elements
• Constants KingJohn, 2, NUS,...
• Predicates Brother, GreaterThan, Round...
• Functions Sqrt, LeftLegOf, FatherOf, Cosin...
• Variables x, y, a, b,...
• Connectives , , , , 
• Equality =
• Quantifiers , 
Shiwani Gupta 34

35. Syntax of predicate logic
Atomic sentence = predicate (term1,...,termn) or term1 = term2
Term = function (term1,...,termn) or constant or variable
Term with no variables is called ground term
E.g. Brother(KingJohn,RichardTheLionheart)
E.g. > (Length(LeftLegOf(Richard)), Length(LeftLegOf(KingJohn)))
E.g. GreaterThan ( Length ( LeftLegOf ( John ) ), ( Length (
LeftLegOf ( Eric ) ) ) )
Shiwani Gupta 35

36. Complex sentences
• Complex sentences are made from atomic
sentences using connectives
S, S1  S2, S1  S2, S1  S2, S1  S2,
E.g. Sibling(KingJohn,Richard) 
Sibling(Richard,KingJohn)
Shiwani Gupta 36

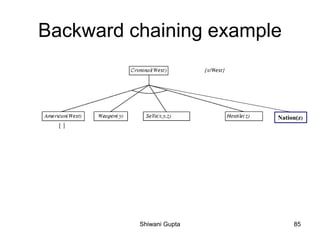
37. Equality
• term1 = term2 is true under a given interpretation if and
only if term1 and term2 refer to the same object
• e.g., definition of Sibling in terms of Parent:
x,y Sibling(x,y)  [(x = y)  m,f  (m = f) 
Parent(m,x)  Parent(f,x)  Parent(m,y) 
Parent(f,y)]
Shiwani Gupta 37

38. Universal quantification
• <variables> <sentence>
Everyone at NUS is smart:
x At(x,NUS)  Smart(x)
• x P is true in a model m iff P is true with x being each possible
object in the model
• Roughly speaking, equivalent to the conjunction of instantiations
of P
Example:
At(KingJohn,NUS) Smart(KingJohn)  At(Richard,NUS)
Smart(Richard)  At(Jesus,NUS) Smart(Jesus) …
Example: “All elephants are gray”
(x )(elephant(x) color(x, GRAY))
Shiwani Gupta 38

39. Existential quantification
• <variables> <sentence>
Someone at NUS is smart:
x At(x,NUS)  Smart(x)
• x P is true in a model m iff P is true with x being some possible
object in the model
• Roughly speaking, equivalent to the disjunction of instantiations
of P
Example:
At(KingJohn,NUS)  Smart(KingJohn)  At(Richard,NUS) 
Smart(Richard)  At(Jesus,NUS)  Smart(Jesus)  ...
Example: “Someone wrote Computer Chess”
(x write(x, COMPUTER-CHESS))
Shiwani Gupta 39

40. Shiwani Gupta 42

41. x loves y Loves(x,y)
Everybody loves Jerry x Loves (x, Jerry)
Everybody loves somebody x y Loves (x, y)
There is somebody whom somebody loves y x Loves (x, y)
Nobody loves everybody  x y Loves (x, y)
There is somebody whom Rita doesn’t love y Loves (Rita, y)
There is exactly one person whom everybody loves
y(x Loves(x,y)  z((w Loves (w ,z) z=y))
There are exactly two people whom Lynn Loves
x y ((xy)  Loves(Lynn,x)  Loves(Lynn,y) z( Loves (Lynn
,z) (z=x  z=y)))
Everybody loves himself or herself x Loves(x,x)
There is someone who loves no one besides herself or himself
x y Loves(x,y)  (x=y)
Examples on FOPL
Shiwani Gupta 43

42. Example
Tony, Mike, John belong to mountaineering
club. Every member of the mountaineering
club is either a skier or mountain climber or
both. No mountain climber likes rain, and all
skiers like snow. Mike dislikes whatever Tony
likes and likes whatever Tony dislikes.
Represent above statements in FOPL
Shiwani Gupta 44

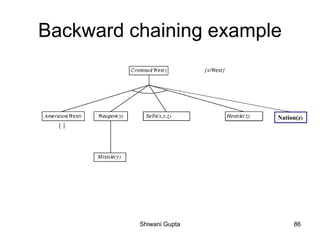
43. Wumpus world in FOL
• the objects in the environment
– terms: constants, variables, functions
• constants:
– times: 0, 1, 2, ...
– headings: R, L, D, U
– coordinates: 1, 2, 3, 4
– locations: 16 squares
– percepts: Stench, Breeze, Glitter, Bump, Scream, None
– actions: Turn(Left), Turn(Right), Forward, Grab, Shoot
– Agent, Wumpus
• functions:
– Square(x,y) // [x,y]
– Home(Wumpus)
– Perception(s, b, g, h, y)
– Heading(t), Location(t)
Shiwani Gupta 45

44. Wumpus world in FOL
• predicates: (true or false)
– properties (of one term/object)
• Breezy(t) // agent feeling breeze at time t
• Breeze(s) // breeze blowing on square s
• Pit(s), Gold(s), etc.
• Time(x) // object x is a time
• Coordinate(x), Action(x), Heading(x), etc.
– relations (of multiple terms/objects)
• At(s,t) // agent on square s at time t
• Adjacent (r,s) // squares r and s are adjacent
• Alive(x,t) // x is alive at time t
• Percept(p,t) // perception at time t
• BestAction(a,t) // action a to take at time t
• term = term: (true or false)
– Home(Wumpus) = [3,3]
– Heading(5) = U
Shiwani Gupta 46

45. Wumpus world in FOL
• the knowledge base
– General knowledge
– Facts that are fixed
– Facts that may change
over time
Atomic
sentences
Compound sentences
Shiwani Gupta 47

46. Exploring Wumpus world in FOL
Deciding the best action: Need to reason about the cave conditions
Diagnostic rules (generate hidden causes from observed effects)
∀s Breezy(s) ⇒ ∃r Adjacent(r,s) Pit(r)
Causal rules (some fact causes certain percepts to be generated)
∀r Pit(r) ⇒ [∀s Adjacent(r,s) ⇒ Breezy(s)]
Shiwani Gupta 48

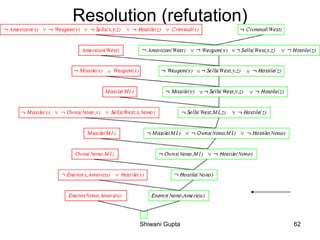
47. First-Order Logic in Wumpus
World
• Suppose an agent perceives a stench,
breeze, glitter at time t = 5:
– Percept([Stench,Breeze,Glitter,None,None],5)
– [Stench,Breeze, Glitter,None,None] is a list
• Then want to query for an appropriate
action. Find an a (ask the KB):
Query:
∀ a BestAction(a,5)
Sol:
a/Grab Shiwani Gupta 49

48. Simplifying the percept and
deciding actions
• Simple Reflex Agent
• Agent Keeping Track of the World
• Reflex
)()],,,,,([,,
)()],,,,,([,,
)()],,,,,([,,
tAtGoldtnonenoneGlitterbsPercepttbs
tBreezetnonenonegBreezesPercepttgs
tStenchtnonenonegbStenchPercepttgb



),()( tGrabActiontAtGoldt 
),(),()( tGrabActiontGoldHoldingtAtGoldt 
),()( tGrabBestActiontGlittert  Shiwani Gupta 50

49. Using logic to deduce properties
• Define properties of locations:
• Diagnostic rule: infer cause from effect
• Causal rule: infer effect from cause
• Neither is sufficient: causal rule doesn’t say if squares far
from pits can be breezy. Leads to definition:
)()(),(,
)()(),(,
lBreezytBreezetlAtAgenttl
lSmellytStenchtlAtAgenttl


),()()( yxAdjacentxPitxyBreezyy 
)(),()(, yBreezyyxAdjacentxPityx 
),()()( yxAdjacentxPitxyBreezyy  Shiwani Gupta 51

50. Inference Rules
• Modus ponens
• Modus Tollens
• And elimination
• And introduction
Shiwani Gupta 52

51. Inference Rules involving Quantifiers
Shiwani Gupta 53

52. An Example Proof of Resolution
• The law says that it is a crime for an American to sell weapons
to hostile nations. The country Nono, an enemy of America, has
some missiles, and all of its missiles were sold to it by Colonel
West, who is American.
• Prove that “West is a criminal” Criminal(West)
Eq. 1
Eq. 2
Eq. 3
Shiwani Gupta 54

53. Assumed FOL
Missiles are weapons
An enemy of America
counts as hostile
West is an American
Nono is a country
Nono an enemy of America
Eq. 4
Eq. 5
Eq. 6
Eq. 7
Eq. 9
Eq. 8
Equations 1 to 9 form knowledge base
Shiwani Gupta 55

54. • Apply Existential elimination to Eq. 2
• From Eq. 10 and AND elimination
• From Eq. 4 and Universal Elimination
• From Eq. 12, 13 and Modus Ponens
• From Eq. 3 and universal elimination
• From Eq. 15, 10 and Modus Ponens
• From eq. 1 and universal elimination (three times)
Eq. 10
Eq. 11
Eq. 12
Eq. 13
Eq. 14
Eq. 15
Eq. 16
Eq. 17
Shiwani Gupta 56

55. • From Eq. 5 and universal elimination
• From Eq. 8, 18 and Modus Ponens
• From Eq. 6, 7, 14, 16, 19 and And-introduction
• From Eq. 17, 20 and Modus Ponens
Eq. 18
Eq. 19
Eq. 20
Eq. 21
Shiwani Gupta 57

56. Crime problem revisited using
canonical form
Put original knowledge base to horn form
Shiwani Gupta 58

57. The Proof
(just in four steps)
Shiwani Gupta 59

58. Resolution (refutation)
Shiwani Gupta 62

59. Unification
Q(x)
P(y) → FAIL
P(x)
P(y) → x/y
P(Marcus)
P(y) → Marcus/y
P(Marcus)
P(Julius) → FAIL
P(x,x)
P(y,y) → (y/x)
P(y,z) → (z/y , y/x)
Shiwani Gupta 64

60. Algorithm: Unify(L1,L2)
1. If L1 or L2 is a variable or
constant, then:
a) If L1 and L2 are identical,
then return NIL.
b) Else if L1 is a variable, then if
L1 occurs in L2 then return
FAIL, else return {(L2/L1)}.
c) Else if L2 is a variable, then if
L2 occurs in L1 then return
FAIL, else return {(L1/L2)}.
d) Else return FAIL.
2. If the initial predicate symbols
in L1 and L2 are not
identical, then return FAIL.
3. If L1 and L2 have a different
number of arguments, then
return FAIL
4. Set SUBST to NIL.
5. For i  1 to number of
arguments in L1:
a) Call Unify with the ith
argument of L1 and the ith
argument of L2, putting result
in S.
b) If S = FAIL then return FAIL.
c) If S is not equal to NIL then:
i. Apply S to the remainder of
both L1 and L2.
ii. SUBST := APPEND(S,
SUBST).
6. Return SUBST.
Shiwani Gupta 65

61. Shiwani Gupta 68

62. 1. Marcus was a man. man(Marcus)
2. Marcus was a Pompeian. Pompeian(Marcus)
3. All Pompeians were Romans.
x: Pompeian(x)→Roman(x)
4. Caesar was a ruler. ruler(Caesar)
5. All Romans were either loyal to Caesar or hated him.
x: Roman(x) → loyalto(x, Caesar) V hate(x,Caesar)
6. Everyone is loyal to someone. x: y: loyalto(x,y)
7. People only try to assassinate rulers they aren't loyal to.
x:y:person(x) ruler(y)  tryassassinate(x,y)→ loyalto(x,y)
8. Marcus tried to assassinate Caesar.
tryassassinate(Marcus, Caesar)
9. All men are people. x: man(x) → person(x)
Shiwani Gupta 69

63. A Resolution Proof
Axioms in clause form:
1. man(Marcus)
2. Pompeian(Marcus)
3.  Pompeian(x1) v Roman(x1)
4. Ruler(Caesar)
5.  Roman(x2) v loyalto(x2, Caesar) v hate(x2,
Caesar)
6. loyalto(x3, f1(x3))
7.  man(x4) v  ruler(y1) v  tryassassinate(x4, y1) v
 loyalto (x4, y1)
8. tryassassinate(Marcus, Caesar)
Shiwani Gupta 70

64. Resolution Proof cont.
Prove: hate(Marcus, Caesar)
hate(Marcus, Caesar)
Roman(Marcus) V loyalto(Marcus,Caesar)
Marcus/x2
5
3
2
7
1
4
8
Marcus/x1
Pompeian(Marcus) V loyalto(Marcus,Caesar)
loyalto(Marcus,Caesar)
Marcus/x4, Caesar/y1
man(Marcus) V  ruler(Caesar) V  tryassassinate(Marcus, Caesar)
 ruler(Caesar) V  tryassassinate(Marcus, Caesar)
 tryassassinate(Marcus, Caesar)
Shiwani Gupta 71

65. Assignment
1 Marcus was a man
2 Marcus was a Pompeian
3 Marcus was born in 40 A.D.
4 All men are mortal
5 All Pompeians died when volcano erupted in 79 A.D.
6 No mortal lives longer than 150 years
7 It is now 1991
8 Alive means not dead
9 If someone dies, then he is dead at all later times
Prove by resolution that Marcus is not alive now
Shiwani Gupta 72

66. Using Resolution with Equality and Reduce
Axioms in clause form:
1. man(Marcus)
2. Pompeian(Marcus)
3. Born(Marcus, 40)
4.  man(x1) V mortal(x1)
5.  Pompeian(x2) V died(x2,79)
6. erupted(volcano, 79)
7.  mortal(x3) V  born(x3, t1) V gt(t2—t1, 150) V dead(x3,
t2)
8. Now=1991
9.  alive(x4, t3) V dead (x4, t3)
10.  dead(x5, t4) V alive (x5, t4)
11.  died (x6, t5) V  gt(x6, t5) V dead(x6, t6)
Prove: alive(Marcus, now)
Shiwani Gupta 73

67. Question Bank• Represent each of these sentences in first-order predicate calculus (FOPL).
– All basketballs are made of rubber.
– Every flower located in Sue’s yard is red.
– At least one question on HW4 was hard.
– All birds can fly except for penguins and ostriches or unless they have a broken wing.
– John’s boss is Mary.
– Selling a book changes who owns it but not who wrote it.
– James father is married to king Johan’s mother
– For all x and all y, if x is the parent of y then y is the child of x
– There is someone who is loved by everyone
– There is noone who does not like icecream
– Spot has atleast two sisters
– Not all students take History and Biology
– Only one student failed in both History and Biology
– There is a barber who shaves all men in town who do not shave themselves
– Well, I like Sandy and donot like Sandy
– One more outburst like that and you will be in contempt of court
– Only one student failed History.
– The best score in History was better than the best score in Biology.
– Every person who dislikes all vegetarians is smart.
– No person likes a smart vegetarian.
– There is a woman who likes all men who are not vegetarians.
– No person likes a professor unless the professor is smart.
– Politicians can fool some of the people all of the time, and they can fool all of the people some of
the time, but they can’t fool all of the people all of the time.
– All Germans speak the same languages
Shiwani Gupta 75

68. University Questions
Consider the following axioms:
All people who are graduating are happy
All happy people smile
Someone is graduating
i. Represent these statements in FOL
ii.Convert each formula to clause form
iii.Prove that “Is someone smiling?” using
resolution technique. Draw the resolution
tree. Shiwani Gupta 76

69. Forward Chaining
• Data driven reasoning
• Agent derives conclusion from incoming
percepts
• It starts from known facts (positive literals)
• If all the premises of an implication are
known then its conclusion is added to set
of known facts
• This process continues till query added or
no further inferences madeShiwani Gupta 77

70. Forward chaining proof
Shiwani Gupta 78

71. Forward chaining proof
Nation(Nono)
Shiwani Gupta 79

72. Forward chaining proof
Nation(Nono)
Shiwani Gupta 80

73. Forward chaining algorithm
Shiwani Gupta 81

74. Backward Chaining
• Goal directed reasoning
• Works backward from query
• Find those implications in KB that
conclude Q
Shiwani Gupta 82

75. Backward chaining example
Shiwani Gupta 83

76. Backward chaining example
Nation(z)
Shiwani Gupta 84

77. Backward chaining example
Nation(z)
Shiwani Gupta 85

78. Backward chaining example
Nation(z)
Shiwani Gupta 86

79. Backward chaining example
Nation(z)
Shiwani Gupta 87

80. Backward chaining example
Nation(z)
Shiwani Gupta 88

81. Backward chaining example
Nation(Nono)
{ }
Shiwani Gupta 89

82. Backward chaining algorithm
Shiwani Gupta 90

83. Knowledge engineering Process in FOL
1. Identify the task (what to talk about)
2. Assemble the relevant knowledge
3. Decide on a vocabulary of predicates,
functions, and constants
4. Encode general knowledge about the domain
5. Encode a description of the specific problem
instance
6. Pose queries to the inference procedure and
get answers
7. Debug the knowledge base
Shiwani Gupta 91

84. The digital circuit domain
One-bit full adder
Input bits
to be added
Carry bit
XOR gates
AND gates OR gate
Sum
Carry bit for
next adder
Shiwani Gupta 92

85. The electronic circuit domain
One-bit full adder
0
1
1
1 0
0
1
1
Shiwani Gupta 93

86. The electronic circuits domain
1. Identify the task
– Does the circuit actually add properly? (circuit verification)
2. Assemble the relevant knowledge
– Composed of wires and gates; Types of gates (AND, OR,
XOR, NOT)
– Irrelevant: size, shape, color, cost of gates
3. Decide on a vocabulary
– Alternatives:
Type(X1) = XOR
Type(X1, XOR)
XOR(X1)
Shiwani Gupta 94

87. Gates or circuits can have one or more input terminals and one
or more output terminals.
E.g. the function In(1,X1) denotes the first input terminal for
gate X1.
Connectivity between gates can be represented by a
predicate:
Connected(Out(1,X1),In(1,X2))
Signal has to be on or off –
Signal(t) this function takes terminal as an argument and returns
the signal value for that terminal.
Two constants – 1 and 0.
Shiwani Gupta 95

88. The electronic circuits domain
4- Encode general knowledge of the domain
• If two terminals are connected they have the same
signal
– t1,t2 Connected(t1, t2)  Signal(t1) = Signal(t2)
• Connected is a commutative predicate
– t1,t2 Connected(t1, t2)  Connected(t2, t1)
• The signal at every terminal is either 1 or 0
– t (Signal(t) = 1)  (Signal(t) = 0)
– 1 ≠ 0
Shiwani Gupta 96

89. • An OR gate’s output is 1 iff any of its inputs is 1
– g Type(g) = OR  Signal(Out(1,g)) = 1
 n Signal(In(n,g)) = 1
• An AND gate’s output is 0 iff any of its inputs is 0
– g Type(g) = AND  Signal(Out(1,g)) = 0  n Signal(In(n,g))
= 0
• An XOR gate’s output is 1 iff its inputs are different
– g Type(g) = XOR  Signal(Out(1,g)) = 1  Signal(In(1,g)) ≠
Signal(In(2,g))
• A NOT gate’s output is different from its input
– g Type(g) = NOT  Signal(Out(1,g)) ≠ Signal(In(1,g))
Shiwani Gupta 97

90. The electronic circuits domain
5. Encode the specific problem instance
Type(X1) = XOR Type(X2) = XOR
Type(A1) = AND Type(A2) = AND
Type(O1) = OR
Connected(Out(1,X1),In(1,X2)) Connected(In(1,C1),In(1,X1))
Connected(Out(1,X1),In(2,A2)) Connected(In(1,C1),In(1,A1))
Connected(Out(1,A2),In(1,O1)) Connected(In(2,C1),In(2,X1))
Connected(Out(1,A1),In(2,O1)) Connected(In(2,C1),In(2,A1))
Connected(Out(1,X2),Out(1,C1)) Connected(In(3,C1),In(2,X2))
Connected(Out(1,O1),Out(2,C1)) Connected(In(3,C1),In(1,A2))
Shiwani Gupta 98

91. The electronic circuits domain
6 - Pose queries to the inference procedure
• What are the possible sets of values of the input of the adder
circuit that lead to a signal of 0 for the sum output bit and a
value of 1 for the carry output terminal?
i1,i2,i3 (Signal(In(1,C1))= i1)  (Signal(In(2,C1)) = i2)
(Signal(In(3,C1)) = i3)  (Signal(Out(1,C1)) = 0 
Signal(Out(2,C1)) = 1)
Answer: (i1 = 1; i2 = 1; i3 = 0) or ((i1 = 1; i2 = 0; i3 = 1) or (i1 = 0;
i2 = 1; i3 = 0)
• What are the possible sets of values of all the terminals of the
adder circuit?
i1,i2,i3,o1,o2 (Signal(In(1,C1)) = i1)  (Signal(In(2,C1)) = i2) 
(Signal(In(3,C1)) = i3)  (Signal(Out(1,C1)) = o1 
Signal(Out(2,C1)) = o2)
7 - Debug the knowledge base
Shiwani Gupta 99