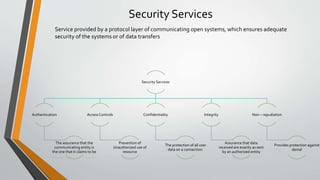
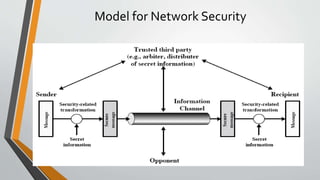
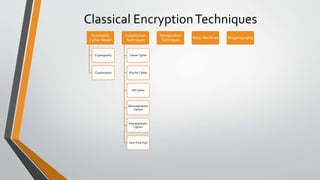
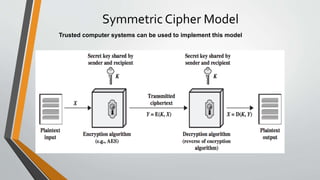
Cryptography is the study and practice of techniques for secure communication in the presence of third parties. It deals with developing and analysing protocols which prevents malicious third parties from retrieving information being shared between two entities. Some key principles of cryptography include confidentiality, data integrity, authentication, and non-repudiation. Cryptography is widely applied in computer security, network security, and internet security. Common techniques include symmetric encryption algorithms, cryptanalysis methods, and the use of substitution and transposition ciphers.

1. UNIT - I
INTRODUCTION &
NUMBERTHEORY

2. INTRODUCTION
• Computer data often travels from one computer to
another, leaving the safety of its protected physical
surroundings.
• Out of hand
• People with bad intention could modify or forge your
data.
• Amusement or for their own benefit
Data
Secured

3. Cryptography
• Cryptography is the study and practice of techniques for secure
communication in the presence of third parties.
• It deals with developing and analysing protocols which prevents malicious
third parties from retrieving information being shared between two entities.

4. Principles of Cryptography
1. Confidentiality refers to certain rules and guidelines usually executed under
confidentiality agreements which ensure that the information is restricted to
certain people or places.
2. Data integrity refers to maintaining and making sure that the data stays accurate
and consistent over its entire life cycle.
3. Authentication is the process of making sure that the piece of data being
claimed by the user belongs to it.
4. Non-repudiation refers to ability to make sure that a person or a party associated
with a contract or a communication cannot deny the authenticity of their
signature over their document or the sending of a message.

5. Where to apply ?
• Computer Security - generic name for the collection of tools
designed to protect data and to hackers
• Network Security - measures to protect data during their
transmission
• Internet Security - measures to protect data during their
transmission over a collection of interconnected networks

6. The OSI Security Architecture
• OSI - open systems interconnection – Provides defined standards of how a data to
be transmitted and received.
• The OSI security architecture is useful as a way of organizing the task of security.
• Computer and communications vendors have developed security features for their
products and services that relate to this structured definition of services and
mechanisms.
• Security attack: Any action that compromises the security of information owned by an
organization.
• Security mechanism: A process (or a device incorporating such a process) that is designed
to detect, prevent, or recover from a security attack.
• Security service: A processing or communication service that enhances the security of the
data processing systems and the information transfers of an organization.The services are
intended to counter security attacks, and they make use of one or more security
mechanisms to provide the service.

7. Security Attacks
Passive attacks
Release of message
contents
Traffic analysis
Active attacks
Masquerade
Re-play
Modification of messages
Denial of service

8. Passive attacks
Release of message contents : Reads content from A to B
Traffic Analysis : Observes pattern of messages from A to B
A B
• Very difficult to detect - do not involve in any
alteration of the data.
• Traffic is sent and received in an apparently normal
fashion and neither the sender nor receiver is aware
that a third party has read the messages or observed
the traffic pattern.
• Feasible to prevent the success of these attacks,
usually by means of encryption.
• The emphasis in dealing with passive attacks is on
prevention rather than detection.

9. Active attacks
Message from hacker
pretending asA
A B
Reads content from A to B
Later replay message to B
A B
Masquerade Re-play

10. Active attacks
Hacker modifies
message from A and
send to B
A B
Disrupts service provided
by server
A
Modification of Message Denial of Service
• It is quite difficult to prevent active attacks - wide variety of potential physical, software, and
network vulnerabilities.
• Goal is to detect active attacks and to recover from any disruption or delays caused by them.

11. Security Services
Security Services
Authentication
The assurance that the
communicating entity is
the one that it claims to be
AccessControls
Prevention of
Unauthorized use of
resource
Confidentiality
The protection of all user
data on a connection.
Integrity
Assurance that data
received are exactly as sent
by an authorized entity
Non – repudiation
Provides protection against
denial
Service provided by a protocol layer of communicating open systems, which ensures adequate
security of the systems or of data transfers

12. Message Authentication
• Receiver must be sure of the sender's identity i.e. the receiver has to make
sure that the actual sender is the same as claimed to be.
• There are different methods to check the genuineness of the sender :
• The two parties share a common secret code word. A party is required to show the
secret code word to the other for authentication. Like in a smuggling movie .
• Authentication can be done by sending digital signature.A trusted third party verifies
the authenticity.One such way is to use digital certificates issued by a recognized
certification authority.

13. Access Control
• In Access Control (or user identification) the entity or user is verified prior to
access to the system resources .

14. Message confidentiality
• Content of a message when transmitted across a network must remain
confidential, i.e. only the intended receiver and no one else should be able
to read the message.
• The users, therefore, want to encrypt the message they send so that an
eavesdropper on the network will not be able to read the contents of the
message.

15. Message Integrity
• Data must reach the destination without any adulteration i.e. exactly as it
was sent.
• There must be no changes during transmission, neither accidentally nor
maliciously.
• Integrity of a message is ensured by attaching a checksum to the message.
• The algorithm for generating the checksum ensures that an intruder cannot
alter the checksum or the message.

16. Message non-reproduction
• Sender must not be able to deny sending a message that it actually sent.
• The burden of proof falls on the receiver.
• Non-reproduction is not only in respect of the ownership of the message,
receiver must prove that the contents of the message are also the same as
the sender sent.
• Non-repudiation is achieved by authentication and integrity mechanisms.

17. Security Mechanisms – Specific
• Hiding or covering data can provide confidentiality. For eg ; Cryptography
steganography are used to enciphering.
Encipherment
• It append a short check value with the data that was created by data itself to a specific
process. Receiver check it by creating a new check value.
Data Integrity
• a cryptographic data transformation that allows a recipient to prove the source and
integrity of the data unit and protect against forgery.
Digital Signature
• Exchange some message to provide their identity to each other.
Authentication Exchange
• Third party will control the communication
Notarization
• We can access the data. For ex id and password/pin
Access control
• Sending data in different Route.
Routing Control
• Insert some blog data to confuse the attacker
Traffic Padding
May be incorporated into the appropriate protocol layer in order to provide some of the OSI security
services

18. Security Mechanisms – Pervasive
• That which is perceived to be correct with respect to some criteria (e.g., as
established by a security policy).
Trusted Functionality
• The marking bound to a resource (which may be a data unit) that names or
designates the security attributes of that resource.
Security Label
• Detection of security-relevant events.
Event Detection
• Data collected and potentially used to facilitate a security audit, which is an
independent review and examination of system records and activities.
Security AuditTrail
• Deals with requests from mechanisms, such as event handling and
management functions, and takes recovery actions.
Security Recovery
Mechanisms that are not specific to any particular OSI security service or protocol layer.

19. Model for Network Security

20. Classical EncryptionTechniques
Symmetric
Cipher Model
Cryptography
Cryptanalysis
Substitution
Techniques
Caesar Cipher
Playfair Cipher
Hill Cipher
Monoalphabetic
Ciphers
Polyalphabetic
Ciphers
One-Time Pad
Transposition
Techniques
Rotor Machines Steganography

21. Symmetric Cipher Model
Trusted computer systems can be used to implement this model

22. Symmetric Cipher Model
A symmetric encryption scheme has five ingredients:
• Plaintext:This is the original intelligible message or data that is fed into the algorithm
as input.
• Encryption algorithm:The encryption algorithm performs various substitutions and
transformations on the plaintext.
• Secret key:The secret key is also input to the encryption algorithm.The key is a value
independent of the plaintext and of the algorithm.The algorithm will produce a
different output depending on the specific key being used at the time.The exact
substitutions and transformations performed by the algorithm depend on the key.
• Ciphertext:This is the scrambled message produced as output. It depends on the
plaintext and the secret key. For a given message, two different keys will produce two
different ciphertexts.The ciphertext is an apparently random stream of data and, as it
stands, is unintelligible.
• Decryption algorithm:This is essentially the encryption algorithm run in reverse. It
takes the ciphertext and the secret key and produces the original plaintext.

23. • There are two requirements for secure use of conventional encryption:
• A strong encryption algorithm
• A secret key known only to sender / receiver
• Cryptographic systems are characterized along three independent dimensions:
• The type of operations used for transforming plaintext to ciphertext -Two general principles:
• Substitution : Element in the plaintext (bit, letter, group of bits or letters) is mapped into another element.
• Transposition : Elements in the plaintext are rearranged.
• The fundamental requirement is that no information be lost (that is, that all operations are reversible). Most systems, referred
to as product systems, involve multiple stages of substitutions and transpositions.
• The number of keys used:
• Both sender and receiver use the same key system is referred to as symmetric, single-key, secret-key, or conventional
encryption.
• Sender and Receiver use different keys, the system is referred to as asymmetric, two-key, or public-key encryption.
• The way in which the plaintext is processed :
• Block cipher : processes the input one block of elements at a time, producing an output block for each input block.
• Stream cipher : processes the input elements continuously, producing output one element at a time.
• The objective of attacking an encryption system is to recover the key in use rather then simply to recover
the plaintext of a single ciphertext.
• Two general approaches to attacking a conventional encryption scheme
• Cryptanalysis : Cryptanalytic attacks rely on the nature of the algorithm.
• Brute-force attack:The attacker tries every possible key on a piece of ciphertext until an intelligible translation into
plaintext is obtained. On average, half of all possible keys must be tried to achieve success.

24. Cryptanalysis -Types of Attacks on Encrypted Messages
Type of Attack Known to Cryptanalyst
Ciphertext only • Encryption algorithm
• Ciphertext
Known plaintext • Encryption algorithm
• Ciphertext
• One or more plaintext-ciphertext pairs formed with the secret key
Chosen plaintext • Encryption algorithm
• Ciphertext
• Plaintext message chosen by cryptanalyst, together with its corresponding ciphertext
generated with the secret key
Chosen ciphertext • Encryption algorithm
• Ciphertext
• Purported ciphertext chosen by cryptanalyst, together with its corresponding decrypted
plaintext generated with the secret key
Chosen text • Encryption algorithm
• Ciphertext
• Plaintext message chosen by cryptanalyst, together with its corresponding ciphertext
generated with the secret key
• Purported ciphertext chosen by cryptanalyst, together with its corresponding decrypted
plaintext generated with the secret key

25. Brute-force attack
• Trying every possible key until an intelligible
translation of the ciphertext into plaintext is
obtained.
• The 56-bit key size is used with the DES (Data
Encryption Standard) algorithm.
• The 168-bit key size is used for triple DES
• Minimum of 128-bit key size can be specified as AES
(Advanced Encryption Standard)
• AverageTime Required for Exhaustive Key Search

26. SubstitutionTechniques
• A substitution technique is one in which the letters of plaintext are replaced
by other letters or by numbers or symbols.
• If the plaintext is viewed as a sequence of bits, then substitution involves
replacing plaintext bit patterns with cipher text bit patterns.

27. SubstitutionTechniques - Caesar Cipher
• Designed by Julius Caesar
• Which involves replacing each letter with the letter standing three places further
down the alphabet
plain: meet me after the toga party
cipher: PHHW PH DIWHU WKHWRJD SDUWB
• A shift may be of any amount, so that the general Caesar algorithm:
C = E(k, p) = (p + k) mod 26
where
k takes on a value in the range 1 to 25.
p is plain text.

28. SubstitutionTechniques - Playfair cipher
• Treats diagrams in the plaintext as single units and translates these units into ciphertext diagrams
• Algorithm is based on the use of 5x5 matrix of letters constructed using a keyword.
• Let the key work be “avengers endgame”
• Split into 2 leter : “av en ge rs en dg am e”
• Remove duplicates and add in the 5x5 matrix and fill rest with ABC….
• Note : I & J should be combined
A V E N G
R S D M B
C F H I K
L O P Q T
U W X Y Z
• Rule 1: Repeating plaintext letters that would fall in the same pair are
separated with a Filler letter such as ‘x’. Like success => su cx es s
• Rule 2 : Plaintext letters that fall in the same row of the matrix are each
replaced by the letter to the right, with the first element of the row
following the last.
• Rule 3: Plaintext letters that fall in the same column are replaced by the
letter beneath, with the top element of the column following the last.
• Rule 4: each plaintext letter is replaced by the letter that lies in its own
row And the column occupied by the other plaintext letter.
Final ciphered text : ve ng an sd ng be nr e

29. SubstitutionTechniques - Hill cipher
• Polygraphic substitution cipher based
on linear algebra.
• Each letter is represented by a
number modulo 26.
• To encrypt a message, each block of n is
multiplied by an invertible n × n matrix,
against modulus 26.
• adapted to an alphabet with any number of
letters
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
• Let say we had defined a key (2x2) as :
• Let say our plain text is “HELP” which when converted to modulo vector:
• Now apply the encryption formula C = K * P mod 26.
• Where K is key, p is plain text.
Then we get chipper text as :

30. SubstitutionTechniques - monoalphabetic cipher
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
A V E N G E R S B C D F H I J K L M O P Q T U V W X
In this cipher method is similar to ceasar cipher, but instead of shifting alphabets n number of times, move the
alphabets by a keyword.
Example: lets say we had choose keyword as “AVENGERS”, then shifted alphabet is as follows :
Now lets say plain text is ENDGAME then using this cipher method we get
E N D G A M E
G I N R A H G

31. SubstitutionTechniques – One-pad cipher
• An encryption technique that cannot be cracked
• Requires the use of a one-time pre-shared key the same size as, or longer than, the message being sent.
• A plaintext is paired with a random secret key (also referred to as a one-time pad).
• Then, each bit or character of the plaintext is encrypted by combining it with the corresponding bit or
character from the pad using modular addition.
• Example:
• Plain text as “AVENGERS”
• Key as “MARVELXX”
• Lets us define numeric for each alphabet
A (0) V(21) E(4) N(13) G(6) E(4) R(17) S(18)
M(12) A(0) R(17) V(21) E(4) L(11) X(23) X(23)
12 21 21 34 10 15 40 41
12 21 21 8 10 15 14 15
M V V I K P O P
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
PlainText (value)
Key (Value)
Message + Key
Modulo of 26
CipherText

32. TranspositionTechniques
• Method of encryption by which the positions held by units of plaintext (which are commonly characters or
groups of characters) are shifted according to a regular system’
• So that the ciphertext constitutes a permutation of the plaintext.
• That is, the order of the units is changed (the plaintext is reordered).
• In the rail fence cipher, the plaintext is written downwards on successive "rails" of an imaginary fence, then
moving up when we get to the bottom.
• Example:
• Let plain text be “WE ARE DISCOVERED. FLEEAT ONCE”
• Which using Rail fence technique can be written as
• Then read off as :
WECRLTEERD SOEEF EAOCA IVDEN

33. Rotor Machines
• An electro-mechanical stream cipher device used for encrypting and
decrypting secret messages.
• Rotor machines were the cryptographic state-of-the-art for a
prominent period of history.
• They were in widespread use in the 1920s–1970s.
• The most famous example is the German Enigma machine, whose
messages were deciphered by the Allies duringWorldWar II, producing
intelligence code-named Ultra.
• The primary component is a set of rotors, also termed wheels or
drums, which are rotating disks with an array of electrical contacts on
either side.
• The wiring between the contacts implements a fixed substitution of
letters, replacing them in some complex fashion.
• Encrypting each letter, the rotors advance positions, changing the
substitution.
• By this means, a rotor machine produces a complex polyalphabetic
substitution cipher, which changes with every keypress.

34. Steganography
• Steganography Greek words- ‘stegos’ meaning ‘to cover’ and ‘grayfia’,
meaning ‘writing’.
• Steganography is a method of hiding secret data, by embedding it into
an audio, video, image or text file.
• Image Steganography –
• Refers to the process of hiding data within an image file.
• The image selected for this purpose is called the cover-image and
the image obtained after steganography is called the stego-
image.
• How is it done?
• An image is represented as an N*M (in case of greyscale images)
or N*M*3 (in case of colour images) matrix in memory, with each
entry representing the intensity value of a pixel.
• In image steganography, a message is embedded into an image
by altering the values of some pixels, which are chosen by an
encryption algorithm.
• The recipient of the image must be aware of the same algorithm
in order to known which pixels he or she must select to extract the
message.

35. FINITE FIELDS AND NUMBERTHEORY

36. Groups
• A groupG, sometimes denoted by {G, .}, is a set of elements with binary
operations denoted as ., that associates to each ordered pair (a,b) of
elements in G an element(a . b) in G, such that the following axioms are
obeyed
• Axioms obeyed
• (A1)Closure : If a and b belong to G, then a.b is also in G
• (A2)Associative law:(a.b).c = a.(b.c)
• (A3)Identity e: e.a = a.e = a
• (A4)Inverse a-1: a.a-1 = e
• (A5)commutative a.b = b.a
• If a group has a finite no. of elements FINITE Group
• Order is equal to the no. of elements in the group
• if commutative a.b = b.a – then forms an abelian group

37. Cyclic Group
• Exponentiation is repeated application of group operator
• example: a3 = a.a.a
• and let identity be: e=a0
• a group is cyclic if every element is a power of some fixed element
• ie b = ak for some a and every b in group

38. Ring
• A ring is a set R equipped with two binary operations + and · satisfying the
following three sets of axioms, called the ring axioms
• R is an abelian group under addition, meaning that:
• (a + b) + c = a + (b + c) for all a, b, c in R (that is, + is associative).
• a + b = b + a for all a, b in R (that is, + is commutative).
• There is an element 0 in R such that a + 0 = a for all a in R (that is, 0 is the additive identity).
• For each a in R there exists −a in R such that a + (−a) = 0 (that is, −a is the additive
inverse of a).
• R is a monoid under multiplication, meaning that:
• (a · b) · c = a · (b · c) for all a, b, c in R (that is, · is associative).
• There is an element 1 in R such that a · 1 = a and 1 · a = a for all a in R (that is, 1 is
the multiplicative identity).
• Multiplication is distributive with respect to addition, meaning that:
• a ⋅ (b + c) = (a · b) + (a · c) for all a, b, c in R (left distributivity).
• (b + c) · a = (b · a) + (c · a) for all a, b, c in R (right distributivity).

39. Field
• A field F, sometimes denoted by {F+x}, is a set of elements with two binary
operations, called addition and multiplication, such that for all a, b, c in F the
following axioms are obeyed
• F is an integral domain – obeys all GROUP & RING Properties.
• multiplicative inverse: For each a in F, except 0, there is an element a‐1 such that
• aa‐1 =(a‐1)a=1
• Division is defined with the following rule:
• a/b = a(b-1)

40. Modular arithmetic
• Modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" upon
reaching a certain value—the modulus
• A familiar use of modular arithmetic is in the 12-hour clock, in which the day is divided into two
12-hour periods.
• If the time is 7:00 now, then 8 hours later it will be 3:00 [(7 + 8) mod 12 = 3]
• Congruence
• a is congruent to b mod n can be written as a≡b (mod n).
• For a positive integer n, the integers a and b are congruent mod(n) if their remainders when divided by n are
the same.
• Another way of defining this is that integers a and b are congruent mod(n) if their difference (a - b) is an
integer multiple of n, that is, if (a-b)/n has a remainder of 0.
Example:
52≡24(mod7)
52 and 24 are congruent (mod 7) because 52(mod7)=3 and 24(mod7)=3.
Note that = is different from ≡.
Example:
36≡10(mod13)
36 and 10 are said to be congruent (mod 13) because their difference
36 - 10 = 26 is an integer multiple of n=13, that is, 26 = 2 x 13.

41. Congruence Properties
Properties of addition in modular arithmetic:
1. If a+b = c, then a (mod N)+b (mod N) ≡c (mod N).
• It is currently 7:00 PM. What time (in AM or PM) will it be in 1000 hours?
• Time "repeats" every 24 hours, so we work modulo 24 to eliminate the days.
• Since 1000≡16+(24×41)≡16(mod24)
• The time in 1000 hours is equivalent to the time in 16 hours.
• Therefore, it will be 11:00 AM in 1000 hours.
2. If a≡b(modN), then a+k≡b+k(modN) for any integer k.
• Find the sum of 31 and 148 in modulo 24.
• 148 is 4 in modulo 24. So, all we need to find is 7+4, which is 11
3. If a≡b(modN) and c≡d(modN), then a+c≡b+d(modN).
• We know that 123≡0(mod3), 234≡0(mod3), 32≡2(mod3), 56≡2(mod3), 22≡1(mod3), 12≡0(mod3), and
78≡0(mod3).
• From property , we have
• 123+234+32+56+22+12+78≡0+0+2+2+1+0+0≡5(mod3).
• Since 5 has a remainder of 2 when divided by 3, so does 123 + 234+ 32+ 56+ 22 + 12 +
78,123+234+32+56+22+12+78, and thus the answer is 22.
4. If a≡b(modN), then −a≡−b(modN).

42. Congruence Properties
Properties of multiplication in modular arithmetic:
1. If a⋅b=c, then a(modN)⋅b(modN)≡c(modN).
• What is (8×16)(mod7)?
• Since 8≡1(mod7) and 16≡2(mod7), we have
• (8×16)≡(1×2)≡2(mod7).
2. If a≡b(modN), then ka≡kb(modN) for any integer k.
3. If a≡b(modN) and c≡d(modN), then ac≡bd(modN).
• Find the remainder when 124⋅134⋅23⋅49⋅235⋅13 is divided by 3.
• We know that 124≡1, 134≡2, 23≡2, 49≡1, 235≡1, and 13≡1.Therefore,
• 124⋅134⋅23⋅49⋅235⋅13≡1⋅2⋅2⋅1⋅1⋅1≡4≡1(mod3),
• implying the product, upon division by 3, leaves a remainder of 1.

43. Congruence Properties
Properties of Exponentiation in modular arithmetic:
• exponentiation is repeated multiplication
• If a≡b(modN), then ak≡bk(modN) for any positive integer k.
• What is 316(mod4)?
• We observe that
• 32≡9≡1(mod4).
• Then by the property of exponentiation, we have
• 316(mod4)​≡(32)8(mod4)≡(1)8(mod4)≡1(mod4).

44. Euclid’s Algorithm
• Euclid's algorithm, is an efficient method for computing the greatest common
divisor (GCD) of two numbers, the largest number that divides both of them
without leaving a remainder.
• The Euclidean algorithm is based on the principle that the greatest common divisor
of two numbers does not change if the larger number is replaced by its difference
with the smaller number.
• For example, lets find GCD of 14 & 10
• GCD(14, 10) = GCD (14,10)
• = GCD (10, 4)
• = GCD (4, 2)
• = GCD (2,0)
• GCD(14, 10) = 2
• Another method:
• 14 = 10x1 + 4
• 10 = 4x2 + 2
• 4 = 2x2 + 0

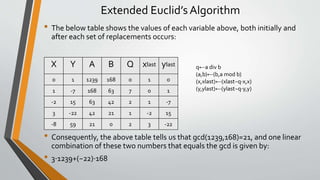
45. Extended Euclid’s Algorithm
• Consider the numbers a=1239 and b=168.Their greatest common divisor (gcd) is 21. Moreover, we can
express 21 as a linear combination of a and b (i.e., as a sum of integer multiples of a and b):
• 21=3⋅1239+(−22)⋅168 [gcd(a,b) = a.x + b.y]
• The Extended EuclideanAlgorithm can be used to find the greatest common divisor (gcd) of two numbers,
and to simultaneously express the gcd as a linear combination of these numbers.Amazingly, this algorithm
finds the greatest common factor of two numbers without ever factoring the numbers! Further, it works
incredibly fast, even on extremely large numbers (with hundreds of digits).The speed at which this
algorithm works coupled with the necessary relative slowness of actually factoring very large numbers lies
at the heart of how modern cryptographic methods work (the same methods that keep your credit card
information safe when you are surfing the internet).
• The algorithm is best explained by example.To find the gcd and an associated linear combination for
a=1239 and b=168 , we do the following:
• First, we initialize some additional variables with the following values: q=0, x=0, y=1, xlast=1, and ylast=0
• Then, while b is not zero, we make the following replacements (in order):
• q←a div b
• (a,b)←(b,a mod b)
• (x,xlast)←(xlast−q⋅x,x)
• (y,ylast)←(ylast−q⋅y,y)
• When we are done, it should be the case that
• gcd(x,y)=xlast⋅1239+ylast⋅168

46. Extended Euclid’s Algorithm
• The below table shows the values of each variable above, both initially and
after each set of replacements occurs:
• xy a b q xlast ylast
• 01 1239 1680 1 0
• 1-7 16863 7 0 1
• -2 15 63 42 2 1 -7
• 3-22 42 21 1 -2 15
• -8 59 21 0 2 3 -22
• Consequently, the above table tells us that gcd(1239,168)=21, and one linear
combination of these two numbers that equals the gcd is given by:
• 3⋅1239+(−22)⋅168
X Y A B Q xlast ylast
0 1 1239 168 0 1 0
1 -7 168 63 7 0 1
-2 15 63 42 2 1 -7
3 -22 42 21 1 -2 15
-8 59 21 0 2 3 -22
q←a div b
(a,b)←(b,a mod b)
(x,xlast)←(xlast−q⋅x,x)
(y,ylast)←(ylast−q⋅y,y)

47. Finite Field
A set F, which is closed under two binary operations, which we denote by "+" and "⋅", is called a field if it
satisfies the following properties:
1. F is associative with respect to addition:
• For all a,b,c∈F, we have a+(b+c)=(a+b)+c
2. F is commutative with respect to addition:
• For all a,b∈F, we have a+b=b+a
3. There is an element in F which we call the additive identity and denote by 0 such that for every a∈F, we
have a+0=a
4. For every a∈F, there exists an element −a∈F which we call the additive inverse of a such that a+(−a)=0
5. F is associative with respect to multiplication:
• For all a,b,c∈F, we have a⋅(b⋅c)=(a⋅b)⋅c
6. F is commutative with respect to multiplication:
• For all a,b∈F, we have a⋅b=b⋅a
7. There is an element in F which we call the multiplicative identity and denote by 1 such that for every a∈F,
we have a⋅1=a
8. For every a∈F, there exists an element a−1∈F which we call the multiplicative inverse of a such that
a⋅a−1=1
9. In F, multiplication distributes over addition in the usual way:
10. For all a,b,c∈F, we have a⋅(b+c)=a⋅b+a⋅c
If a field F contains only a finite number of elements, we say that F is a finite field.

48. Polynomial Arithmetic
• Why study polynomial arithmetic?
• Defining finite fields over sets of polynomials will allow us to create a finite
set of numbers that are particularly appropriate for digital computation.
• Since these numbers will constitute a finite field, we will be able to carry out
all arithmetic operations on them — in particular the operation of division —
without error.
• In general, a polynomial is an expression of the form:
• anxn + an−1xn−1 + ...... + a1x + a0
• for some non-negative integer n and where the coefficients a0, a1, ...., an are drawn
from some designated set S. S is called the coefficient set.
• When an not 0, we have a polynomial of degree n.
• A zeroth-degree polynomial is called a constant polynomial.
• Polynomial arithmetic deals with the addition, subtraction, multiplication, and division
of polynomials.

49. Polynomial Arithmetic Operations
• We can add two polynomials:
• f(x) = a2x2 + a1x + a0
• g(x) = b1x + b0
• f(x) + g(x) = a2x2 + (a1 + b1)x + (a0 + b0)
• We can subtract two polynomials:
• f(x) = a2x2 + a1x + a0
• g(x) = b3x2 + b0
• f(x) − g(x) = (a2−b3 )x2 + a1x + (a0 − b0)
• We can multiply two polynomials:
• f(x) = a2x2 + a1x + a0
• g(x) = b1x + b0
• f(x) × g(x) = a2b1x3 + (a2b0 + a1b1)x2 + (a1b0 + a0b1)x + a0b0
• We can divide two polynomials (result obtained by long division):
• f(x) = a2x2 + a1x + a0
• g(x) = b1x + b0
• f(x) / g(x) = ? (See next slide)
+ 7

50. Polynomial Arithmetic Operations – Division
• USING LONG DIVISION:
• Let’s say we want to divide the polynomial
• 2x2 + 3x – 1 / x + 1
• In this example, our dividend is 2x2 + 3x - 1 and the
divisor is x + 1.
• We now need to find the quotient.
• Long division for polynomials is as follows:

51. Prime numbers
• prime numbers only have divisors of 1 and self
• they cannot be written as a product of other numbers
• note: 1 is prime, but is generally not of interest
• eg. 2,3,5,7 are prime, 4,6,8,9,10 are not
• prime numbers are central to number theory
• list of prime number less than 200 is:
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79
83 89 97 101 103 107 109 113 127 131 137 139 149 151 157 163
167 173 179 181 191 193 197 199

52. Fermat’s little theorem
• Fermat’s little theorem states that if p is a prime number, then for any integer a, the number a p – a is an integer
multiple of p.
• Here p is a prime number
ap ≡ a (mod p).
• Special Case: If a is not divisible by p, Fermat’s little theorem is equivalent to the statement that
• a p-1 -1 is an integer multiple of p.
• ap-1 ≡ 1 (mod p)
OR
ap-1 % p = 1
Here a is not divisible by p.
• Examples:
• P = an integer Prime number & a = an integer which is not multiple of P
• Let a = 2 and P = 17 . According to Fermat's little theorem
• 2 17 - 1 ≡ 1 mod(17)
• we got 65536 % 17 ≡ 1
• that mean (65536-1) is an multiple of 17
• Use of Fermat’s little theorem
• If we know m is prime, then we can also use Fermats’s little theorem to find the inverse.
• am-1 ≡ 1 (mod m)
If we multiply both sides with a-1, we get
• a-1 ≡ a m-2 (mod m)

53. Euler'sTheorem
• There is a natural question to ask upon discovering Fermat's LittleTheorem, "What
happens when the modulus is not prime?“ in ap−1≡1(mod p).
• Euler’sTheorem :
• If n is a positive integer and a is an integer with gcd(a,n)=1, then aφ(n)≡1(modn).
• we start with the set of products given by
• a⋅r1,a⋅r2,a⋅r3,…,a⋅rφ(n)
• where r1,r2,r3,…,rφ(n) are the positive integers less than n that are relatively prime to n.
• Theorem may be used to easily reduce large powers modulo n.
• For example, consider finding the ones place decimal digit of 7222
• i.e. 7222 mod (10). Note that 7 and 10 are coprime, φ(10)=4.
• So Euler's theorem yields 74 ≡1 (mod 10), and we get 7222 ≡ 74x55+2 ≡ (74)55 x 72 ≡ 155x72 ≡
49 ≡ 9 (mod 10).
• Euler's theorem is sometimes cited as forming the basis of the RSA encryption system.
• however it is insufficient (and unnecessary) to use Euler's theorem to certify the validity
of RSA encryption, where we use Chinese RemainderTheorem

54. Chinese RemainderTheorem
• States that if one knows the remainders of the Euclidean division of
an integer n by several integers, then one can determine uniquely the
remainder of the division of n by the product of these integers, under the
condition that the divisors are pairwise coprime.
• The Chinese remainder theorem is widely used for computing with large
integers, as it allows replacing a computation for which one knows a bound
on the size of the result by several similar computations on small integers.
• Theorem
• Let m and n be integers where gcd(m,n)=1, and let b and c be any
integers.Then the simultaneous congruences
x≡b(modm)andx≡c(modn)
• have exactly one solution with 0≤x<mn.
Sunzi's original formulation: x ≡ 2 (mod 3) ≡
3 (mod 5) ≡ 2 (mod 7) with the solution x =
23 + 105k where k ∈ ℤ

55. Discrete Logarithms
• The inverse problem to exponentiation is to find the discrete
logarithm of a number modulo p
• that is to find x such that y = gx (mod p)
• this is written as x = logg y (mod p)
• if g is a primitive root then it always exists, otherwise it may not, eg.
x = log3 4 mod 13 has no answer
x = log2 3 mod 13 = 4 by trying successive powers
• whilst exponentiation is relatively easy, finding discrete logarithms is
generally a hard problem.