Soft Computing is particularly valuable for solving difficult (non-linear) real-world problems in areas like pattern recognition, control systems, decision making, and optimisation where noisy/incomplete/dubious data dominates - and especially where mathematical models are inadequate or too complex. Today it is widely used in areas ranging from image processing and robotics, to military target recognition and financial modelling, medical diagnosis and speech/conversation recognition and recovery et al. Soft Computing: A Comprehensive Outline Soft Computing Definition Soft computing represents a collection of computational methodologies that aim to exploit the tolerance for imprecision, uncertainty, and partial truth to achieve tractability, robustness, and low-cost solutions. Unlike traditional "hard" computing approaches that demand precise, crisp, and mathematically rigorous algorithms, soft computing embraces approximate reasoning and heuristic problem-solving techniques. The field emerged in the late 20th century as researchers recognized that many real-world problems are too complex, ill-defined, or computationally intractable for conventional analytical methods. The fundamental philosophy of soft computing lies in mimicking human-like reasoning processes, which naturally handle uncertainty and imprecision. Humans make decisions based on incomplete information, learn from experience, and adapt to changing environments—capabilities that soft computing seeks to replicate in artificial systems. This approach has proven particularly valuable in domains where traditional mathematical models fail or become computationally prohibitive. Core Components/Methodologies Fuzzy Logic Systems Fuzzy logic, pioneered by Lotfi Zadeh in 1965, forms one of the foundational pillars of soft computing. Unlike classical Boolean logic that operates with binary true/false values, fuzzy logic allows for degrees of truth between 0 and 1. This approach better represents human reasoning, where concepts like "tall," "warm," or "fast" exist on continuous scales rather than discrete categories. Fuzzy systems consist of three main components: fuzzification (converting crisp inputs into fuzzy sets), inference engine (applying fuzzy rules), and defuzzification (converting fuzzy outputs back to crisp values). These systems excel in control applications, decision-making processes, and pattern recognition tasks where linguistic variables and expert knowledge can be effectively incorporated. Neural Networks and Deep Learning Artificial neural networks draw inspiration from biological neural systems, particularly the human brain's structure and function. These networks consist of interconnected nodes (neurons) that process information through weighted connections, learning patterns through training processes. The fundamental strength of neural networks lies in their ability to approximate complex nonlinear functions and learn from examples without explicit programming.

1. Advanced
SOFT COMPUTING
Analogue - Digital - Hybrid - Quantum
Professor Peter Cochrane OBE, DSc
www.petercochrane.com

2. POSITIONING
Soft Computing is particularly valuable for solving di
ffi
cult (non-linear) real-world
problems in areas like pattern recognition, control systems, decision making, and
optimisation where noisy/incomplete/dubious data dominates - and especially where
mathematical models are inadequate or too complex. Today it is widely used in areas
ranging from image processing and robotics, to military target recognition and
fi
nancial
modelling, medical diagnosis and speech/conversation recognition and recovery et al.

3. • At a fundamental level our universe is non-linear, di
ffi
cult to understand, and hard to model
• We are essentially limited linear thinkers and prefer simple explanations/approximations
• Our closed form mathematical modelling techniques are bounded by 5 variables
• Some of our most challenging problems can present well over 100 variables
• All our analogue and digital computing techniques are fundamentally
fi
nite
• No matter how big; our digital computers ultimately hit the limits of scale
• Quantum computing sees new opportunities in new and old domains
• Quantum computing is probabalistic and a hybrid processing form
• There is nothing quite as powerful as a really good approximation
• We are now at a stage where many problems demand a mix of techniques
• It is prudent to start any analysis at a simple level and slowly build in complexities
• Before addressing a problem it is worth considering what a reasonable answer might be!
“There are no solutions to really complex problems,
and we often have to accept approximations and dynamic results”
AXIOMS

4. AXIOMS
“Simplicity is complexity resolved”
“Simplicity is often hard won on the basis of deep understanding”

5. Example challenge
Three Body Problem
The three-body problem has no general closed form solution, meaning there is no equation
that always solves it. When three bodies orbit each other, the resulting dynamical system is
chaotic for most initial conditions.
Because there are no solvable equations for most three-body systems, the only prediction
for the motions of the bodies is to estimate them using numerical/analogue computing,
and physical modelling methods.
Our solar system turns out to be at a ‘point
of stability’ that emerged out of the cosmic
chaos…along with billions of other systems
in the Cosmos …
Newton was confounded by this apparently simple problem and was unable to derive a
general solution…a nor has anyone else!

6. 3B Problem
A n i m at i o n
The Cosmos was initially in a state of chaotic flux, but as
it expanded multiple points of stability emerged to see the
emergence of galaxies and solar systems
It turns out that this is a common phenomenon
throughout cosmology, biology, chemistry, physics - it is
just that it escapes our mathematic framework - however,
we can model/simulate with digital computers, analogue
computers and physical models…

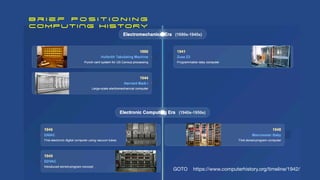
7. The term Soft Computing (SC) was initially coined by Zadeh [1992]. SC aims at
fi
nding the
closest approximate solution to problems via computationally robust, e
ffi
cient, and cost
e
ff
ective methods. Most of the techniques are actually quite basic, with some stretching
back to the era of electro-mechanical control theory and practice. Perhaps the most
signi
fi
cant techniques are those inspired by biological phenomena including life,
reproduction, intelligence and sociological behaviours.
The advent of SC was marked by research in machine learning, probabilistic reasoning,
arti
fi
cial neural networks (ANN), fuzzy logic [Jang 1997] and genetic algorithm (GA). Today,
the purview has been extended to include swarm intelligence and foraging behaviours of
biological populations with algorithms like the particle swarm optimisation (PSO) and
bacterial foraging algorithm (BFO) [Holland 1975]. Some practitioners have also explored
and used biological elements (ie insects and worm brain bio-components in vitro) into the
SC loop with some signi
fi
cant successes. To date, Quantum Computing has not entered
the fray, but we might anticipate it being drawn into this
fi
eld as it is fundamentally
probabilistic and of a hybrid analogue-digital form.
Soft Computing
A rich history

8. B r i e f P o s i t i o n i n g
COMPUTING HISTORY https://www.computerhistory.org

9. https://www.computerhistory.org/timeline/1942/
GOTO
B r i e f P o s i t i o n i n g
COMPUTING HISTORY

10. B r i e f P o s i t i o n i n g
COMPUTING HISTORY

11. “In 2024 the USA led this
fi
eld with error correction,
and coherence times for 100-200 Qbits. BUT this
lead was shattered in 2025 by China with 2000 Qbits
reported. China is investing in more academic and
industry R&D, whilst USA programs appear to be
hindered by politically motivated activities”
“This Google quantum supremacy demonstration is
strongly contested by many as the demonstration
was a ‘mathematical puzzle biased to work’ and had
no real world application”
B r i e f P o s i t i o n i n g
COMPUTING HISTORY

12. A collection of computational techniques, primarily founded in AI, Arti
fi
cial Life, Life, and
Genetics, that embrace imprecision and uncertainty to solve complex problems. Unlike
conventional computing; approximate, workable,
fi
t-for-purpose, robust, cost-e
ff
ective
solutions are the target, especially when dealing with confounding real-world scenarios
where exact solutions are extremely di
ffi
cult, too costly/impossible to compute.
SC Definition(s)
A group of computational techniques based on arti
fi
cial intelligence and natural selection
that provides quick and cost e
ff
ective solution to very complex problems for which
analytical (hard computing) formulations do not exist.
Analogue computing was a pre-cursor; initially realised in mechanical, electro-
mechanical, and electronic simulators of speci
fi
c mechanisms and problems. Today it is a
somewhat obscure art applied where there really are no alternatives. Just two examples:
the tidal movement of sediment in an estuary; and modelling/solving the balance problems
of anthropomorphic and zoomorphic robots.
+ Many More Similarly!

13. SAMPLE APP AREAS
Dynamic Control Systems: Automation, robotics, intelligent weapons, radar recognition.
Machine Learning: Neural networks, fuzzy systems, evolutionary algorithms
Data Mining: Finding patterns in large, noisy datasets
Knowledge Discovery: Extracting meaningful information from incomplete or uncertain data
Signal Processing: Image enhancement, feature extraction, pattern and noise
fi
ltering
Finance and Risk: Credit scoring, market prediction, portfolio optimisation, fraud detection
Medical Diagnosis: Image analysis, diagnostics, drug discovery, and treatment planning
Logistics: Tra
ffi
c management, route optimisation, and supply chain management.
Manufacturing: Process optimisation, defect detection, predictive maintenance, scheduling
Telecoms: Net optimisation, resource allocation, error correction, adaptive signal processing
Environmental: Weather, pollution monitoring, ecological modelling, resource management
Stochastic Forecasting: Crime, con
fl
ict, markets, behaviours +++ strategic decision making
“Soft Computing’s strength is handling real-world problems involving uncertainty, incomplete
information, and complex nonlinear relationships that are too di
ffi
cult to mathematically model”

14. Imprecision and Uncertainty:
Coping with the unknown, ambiguity, vagueness, partial truths and expectations
Approximation and Robustness:
Focus on
fi
nding good, reliable approximations that work well in practice
Cost-Effectiveness:
Computationally e
ffi
ciency, saving time, energy and resources are prime
Flexibility:
Adaptable to di
ff
erent problem domains, a range of inputs, including noisy or incomplete data
Fuzzy Logic:
Reasoning and decision-making under great uncertainty using fuzzy sets/rules (Japanese origins)
Neural Networks:
Learn from data and can be used for pattern recognition, prediction, and classi
fi
cation.
Genetic Algorithms:
Employs natural selection and evolutionary processes to
fi
nd near-optimal solutions
Probabilistic Reasoning:
Adapted to deal with stochastic uncertainty and incomplete data to make decisions on the
fl
y
SC Environment
Characteristics
In extreme cases we can be reduced to ‘serial guesses’
and sequential iterations converging on very limited
‘near enough is good enough’ results!

15. USE CASE 1:
Problem: Improving the spray painting process where multiple variables a
ff
ect quality -
temperature, humidity, air pressure, viscosity, robot speed, and spray gun control.
Traditional control systems struggled because:
•The relationships between variables are complex and nonlinear
•Environmental conditions change throughout the day
•Di
ff
erent paint types required di
ff
erent approaches
•Human operators made intuitive adjustments that were hard to codify
A car manufacturer needed to optimise their paint booth operation
Application: The company implemented a soft computing solution combining:
•Fuzzy logic handle imprecise rules of temperature, humidity, paint
fl
ow interaction
•Neural networks trained on data from experts to learn optimal parameter combos
•Genetic algorithms continuously optimise the overall process parameters

16. Clean and dry process designed and improved
by man; spray process human tutored ML(?)
and continually optimised by feedback from
inspection, correction and
fi
nal end quality
P r o c e ss S t e p :
Clean, Dry, Spray

18. ML records and analyses detected/corrected
blemishes to feed-back into previous stages
for investigation and process correction(s)
P r o c e ss S t e p :
Inspection polish

20. USE CASE 1
Outcome:
•Paint defect rates dropped by 40%
•Paint consumption reduced by 15% through continual optimisation
•Consistency improved signi
fi
cantly across di
ff
erent shifts/operators
•The system adapted automatically to seasonal changes & conditions
•Setup time for new paint types decreased from many hours to minutes
•New car model set up takes a day/s of Human-ML interworking/optimisation
Some problems are so complex, so demanding, so expensive, it easier/more economic
to continually track and correct at every stage with the
fi
nished product the
fi
nal arbiter!
The key advantage is that the SC approach can handle the "messy" real-world
conditions and human expertise that traditional rigid control systems can’t manage
e
ff
ectively. Instead of requiring precise mathematical models of paint behaviour, it
learned from experience and handled uncertainty naturally.

21. USE CASE 2:
Problem: Hospital's radiology departments struggle with breast cancer screening from
mammograms. Radiologists have to examine thousands of images, but:
•Early-stage tumours are extremely subtle and easy to miss
•False positives cause unnecessary anxiety and expensive follow-up procedures
•Radiologist fatigue sees inconsistent diagnoses as the norm
•There is a shortage of experienced radiologists
•Each case require the analysing of complex patterns in grainy, low-contrast, images
Health system seeing more demand and fewer quali
fi
ed sta
ff
Application: Hospitals are deploying soft computing diagnostics combing:
•Neural networks trained on thousands of mages with known outcomes
•Fuzzy logic deals with uncertain classi
fi
cations like "suspicious" or "abnormal"
•Evolutionary algorithms optimise feature detection parameters for di
ff
erent tissue

22. ML records and analyses detected/corrected
blemishes to feed-back into previous stages
for investigation and process correction(s)
S tat u s Q U O

24. Problem: Hedge fund trying to develop an automated trading system for foreign
exchange markets. The challenges are enormous:
•Markets are in
fl
uenced by countless unpredictable and ill understood factors
•Mathematical models mostly fail badly during periods of market volatility
•Traders make pro
fi
table intuitive decisions that can't be easily programmed
•Market conditions change rapidly, making
fi
xed rules obsolete
•Risk management requires balancing potential pro
fi
ts against catastrophic losses
USE CASE 3: Automation of markets and trading processes
Application: They built a soft computing trading system using:
•Fuzzy logic interprets market indicators like "trend weakening" or "volatility highs”
•Neural networks trained on years of market data to recognize complex patterns
•Genetic algorithms optimise trading strategies continuously as market change
•Probabilistic reasoning for risk assessment and position sizing

25. USE CASE 3
Trader
DESK 24
Tracking < 6
key stocks at
the same time
plus The Fed -
SC knows no
such limits!
>75% of US
trades made
by machines!
>70% of UK
trades made
by machines!

26. USE CASE 3
Trader
DESK 24
Tracking < 6
key stocks at
the same time
plus The Fed -
SC knows no
such limits!
>75% of US
trades made
by machines!
>70% of UK
trades made
by machines!
The biggest Risk IS?
Entanglement or THE
SYNCHRONY of A DOMINANt
Machine Type
A catastrophic
LIMIT cycle would
take down the markets
in minutes

27. USE CASE 3
Outcome:
•Generated consistent 23% annual returns over 3 years, outperforming other models
•Reduced maximum drawdown (worst losses) by 45% through better risk management
•Adapted to major market events like Brexit and COVID-19 with no human intervention
•Cut research time for new trading strategies from months to weeks
•System learned to avoid trades during highly unpredictable periods, preserving capital
The key breakthrough was the abandonment of exact price movement prediction as SC
learned to recognize favourable probability patterns and manage uncertainty. It handled
"human-like" aspects of trading - reading market sentiment, adapting to conditional
changes, and making decisions with incomplete information - while executing trades at
superhuman speed and consistency.

28. USE CASE 4:
Problem: Barcelona had tra
ffi
c congestion that tra
ffi
c light systems couldn't handle
- people were living in crowded conditions with no pedestrian areas
- pollution, air quality, and noise levels were also unacceptable
•Tra
ffi
c patterns changed unpredictably due to events, weather, accidents, construction..
•Fixed tra
ffi
c light timing caused unnecessary delays, frustration and emissions
•Emergency vehicles struggled to get through congested intersections
•Rush hour always created chronic gridlock that lasted for hours
•Air pollution from idling vehicles was creating a health crisis
City tra
ffi
c & people congestion created by medieval/victorian eras
Application: A city-wide soft computing tra
ffi
c management system was installed:
•Fuzzy logic at each intersection enabled adaptable dynamic decisions
•Neural networks learned tra
ffi
c patterns from thousands of sensors, cameras, GPS
•Evolutionary algorithms continuously optimised tra
ffi
c light coordination city wide
•Probabilistic models forecast tra
ffi
c based on time, weather, events, history..

29. USE CASE 4: Transformation Planning
•At
fi
rst inspection the geometry looks like a ‘containment nightmare’
•Extensive studies/analysis of all tra
ffi
c and social activities undertaken
•The need for an increase in the number of pedestrian areas became apparent
•Restrictions of the number of vehicle path options with more major arteries forecast
•Investments in more e
ff
ective public transport emerged as an urgent requirement
•Counterintuitively, more autonomy for pedestrians, cyclists, and vehicles emerged
•Perhaps the biggest bonus was to be more green, social, and trading spaces…

30. USE CASE 4: MODELLING Traffic

31. USE CASE 4: MODELLING Pedestrians

32. USE CASE 4

33. USE CASE 4
Outcome:
•Average commute times reduced by 21% across the city
•Vehicle emissions dropped by 18% due to less stop-and-go tra
ffi
c
•Emergency response times improved by 35% with dynamic priority routing
•Fuel consumption decreased by 15% as vehicles spent less time idling
•The system automatically adapted to special events like football matches or festivals
•Pedestrian wait times at crosswalks were optimised, improving walkability
SC was essential because tra
ffi
c is inherently unpredictable with behaviours that can't be
captured by rigid mathematical models. The system learned to "think" like an experienced
tra
ffi
c controller intuitively knowing when to ‘bend’ the rules, but could do so across
thousands of intersections simultaneously while considering the entire city's tra
ffi
c
fl
ow as
one integrated system.

34. SEgUe: HUMANITY @ HOME
Getting it right !
2025 > 55% live in cities/urban areas
2050 > 70% will live in cities/urban areas
Global Population
2025 ~ 8Bn
2050 <7Bn
2050 >10Bn Strained resources
Old populations

35. USE CASE 5:
Problem: Many 1990s telco’s were mid-optical
fi
bre/network digitisation when it became
imperative to streamline/transform all installation and maintenance operations to meet a
wider range of technical and customer demands at a much reduced cost
•An analogue copper era where all operatives had all the skills was coming to an end
•The speed of tech transformation was rendering individuals untrained and wanting
•Equipments were being rolled out faster than training courses could be organised
•The variety/con
fi
guration of equipments became more than a reasonable van stock
•Customer demand migrated from 9am - 5pm to 24 x 7 ‘mission critical’
•A ‘travelling salesman’ (TSP) problem within the grasp of a human controller was
mutating to a ‘travelling salesman problem in n-dimensions’ with no known solutions !
Telco inadequate ‘Man-in-Van maintenance/support operations
Application: The TSP is ’N-P Complete’ with no ‘closed-form’ solution for small numbers
of nodes, let alone a highly dynamic (stochastic) man-in-van
fl
eet numbering >20,000
•AI at this time was relatively juvenile at this time and o
ff
ered no obvious solution rout
•Arti
fi
cial Life (AL) was the only investigative route that appeared to o
ff
er some hope…

36. USE CASE 5:
• Accuracy of report/request lodged by the customer
• Remote diagnosis testing and checking uncertainties
• Variations of agreed customer availability and site access
• Man-in-Van (MiV) availability, timing, mobility and ‘locality’
• MiV training, knowledge and capability
fi
t the perceived task
• The tools and equipment thought necessary are on board
• MiV availability with weather and road conditions permitting
• Any health and safety issues that may impact the operation
• Priority spanning customer inability through to a life threatening emergency
• Initial on site diagnosis con
fi
rms/changes report/request and the actual need
• MiV can/cannot adapt to cope with the diagnosis and ful
fi
l a full, or partial,
fi
x
• IFF the man on site cannot a
ff
ect a
fi
x, is the necessary back up available to help
• +++
Unknowns and uncertainties
What follows is a ‘short list’ of the many variables confronting the field management
teams along with their operatives trying to satisfy the immediate needs of installation,
faults, failures, and upgrades for customers…

37. USE CASE 5:
• Prior Art: was almost non-existent with just a few practitioners @ Santa Fe Institute,
MIT, and Georgia Tech. It was pretty much virgin territory and clearly a long shot!
• A multi-discipline, multi-ethnic group of Math, Physics, Engineering, Entomology,
Biology and Biochemistry PhDs was recruited with the task of investigating, modelling
and characterising Slime Mould, ants and swarms in the process of performing basic
tasks and solving various maze problems
• Within a couple of months we had su
ffi
cient to start in on the basic TSP
Initial best guess: GOTO Moulds, Ants, and Swarm Intelligence
• Sacri
fi
cing 5 - 10% of predictions accuracy yielded results faster than super computers
• Extending to ~20k nodes was spectacularly successful, and so it was out to 20M+ !
• We now needed new thinking on how to speed up the evolution into n-dimensions
Successes came thick and fast:

38. ANTS
TSP solution
Perspective

39. Slime Mold

40. ANTS

41. Protocol As I recall
from 35 Years ago !
Each Ant
- Random search for a node
- Lay a trail node-to-node
- Repeat until ’n’ - nodes linked
All Ants
Either hermaphrodite parents, or
Children produced by ’N' parents
Genetics
Parents carry a complete/incomplete
subset of several seed search and
fi
nd,
share, collaborate instructions sets
Parents remain unmodi
fi
ed, but children
Inherit a signi
fi
cant sample of the ’N’
subsets originally available

42. The genetic mix and
Natural selection
Sexual Mixing Process
All parents engage in one
giant engagement to share
code which manifests in the
resulting children
Parents
The capability of each parent has already been
established & performance metrics assigned
Children
The capability of each is established in the
same manner as per the parent group
(Un)natural Selection
The new expanded population Survival contest:
- All children better than any parent survives
- All parents worse than any child is sacri
fi
ced
- All surviving children promoted to parents
- The cycle is repeated ‘M’ times until stable

43. Starting with a
10k population
The OUTCOME
Culling
Genetic
Mixer
Top y%
Children
Top x%
Parents
In just 30 - 34 cycles the optimum of
4 parents emerged to deal with the
numerous variables and 20k mobile
nodes simultaneously
At this point we achieved results faster
than any super computer: and accurate
to within 10% of the optimum, which
was less than the error on many of the
customer metrics!

44. USE CASE 4
Outcome:
•Year one roll out saw a £200M saving
•As the
fi
bre and digitalisation roll out continued further saving mounted rapidly
•Another deployment was engineered for tra
ffi
c management in a US network
•This saw a doubling of their capacity for no investment in hardware
•The system automatically adapted to change in real time and never su
ff
ered indigestion!
This SC approach was essential because of the inherent complexity, scale, and diverse
unpredictability of near 100 parameters in
fl
uencing the
fi
nal outcome. Sad to say, within
a few years, new managers and engineers, reverted to a ‘non-intelligent solution on the
basis that they could not understand what had been done or how it worked!

45. So, What Next ?
Apart from Moore’s Law seeing
atoms and/or new material
combinations processing and
storing bits faster and denser, there
are two big game changers that
have the potential to transform SC
during your lifetime…

46. SELF Programming And
auto-collaborative AI
MSoft Code now >30% written by AI
Google Code now >40% written by AI
“Collaborative AI is an emergent property that
has yet to make itself fully visible and useful”
GOTO: https://tinyurl.com/3kx4japt
Could this be the start of a new era in hard/soft
computing: self creation by letting AI o
ff
the
leash and applying the basic
principles of evolution?

47. OPEN ENDED EXPLORATION,
Using recursive agents 1.1
MSoft Code now >30% written by AI
Google Code now >40% written by AI

48. Genetic Programming for Code Evolution - Agents use genetics to evolve their codebases, with
functions/modules mutating, based on performance metrics like execution speed, memory usage, or
task completion rates.
Fitness-Based Selection - Self-improving agents implement
fi
tness functions that evaluate di
ff
erent
versions of their code against benchmarks, automatically selecting and propagating the most
successful variants while discarding underperforming iterations.
Distributed Evolution Across Communities - Open source projects leverage contributions from
multiple developers as a form of parallel evolution, where di
ff
erent branches and forks represent
evolutionary paths that compete and merge based on community adoption and testing.
Automated Code Mutation/Testing - Agents systematically introduce small random changes to
codebases, run comprehensive test suites, retaining modi
fi
cations that improve functionality while
reverting harmful fails
OPEN ENDED EXPLORATION,
Using recursive agents 1.1
MSoft Code now >30% written by AI
Google Code now >40% written by AI

49. OPEN ENDED EXPLORATION,
Using recursive agents 2.1

50. Meta-Learning for Optimisation Strategy Evolution - Advanced agents simultaneously evolve their
code & learning algorithms to develop increasingly sophisticated methods for self-modi
fi
cation
Swarm Intelligence in Code Development - Multiple agents collaborate to explore di
ff
erent solution
spaces simultaneously, sharing successful adaptations through mergers and collective code reviews
Adaptive Architecture Evolution - Agents dynamically restructure their system architectures, evolving
from monolithic designs to micro-services or changing neural network topologies based on performance
feedback
Community-Driven Selection - Open source communities act as environmental selection forces, where
user feedback, bug reports, and feature requests guide the evolutionary direction of self-improving
agents
Emergent Behaviour Through Recursive Improvement - Agents develop emergent capabilities along
with optimisation strategies that weren't explicitly programmed, leading to novel solutions/evolutionary
paths
OPEN ENDED EXPLORATION,
Using recursive agents 2.1

51. OPEN ENDED EXPLORATION,
Using recursive agents 2.2
Curiosity-Driven Discovery - Self-improving agents develop intrinsic motivation rewarded by
exploration of novel states/unexpected outcomes, leading to non-predetermined/preprogrammed
research directions, often discovering emergent phenomena through autonomous experimentation
Recursive Agents continuously evolve their innovation methodologies, to develop increasingly
e
ff
ective approaches to creativity and problem-solving that compound over time
Unbounded Expansion - Rather than optimising within
fi
xed parameters; agents pro-actively expand
the problem domains with new questions, generating novel hypotheses, and creating new
fi
elds of
inquiry
Emergent Tools - Agents spontaneously develop new languages, frameworks, abstractions to meet
their evolving needs & create increasingly powerful tools able to tackle previously impossible
challenges
Cross-Domain Synthesis - Agents exploit disparate
fi
elds by applying insights from one to another,
leading to breakthrough innovations arising from unexpected combinations and methodologies

52. OPEN ENDED EXPLORATION,
Using recursive agents
Hypothesis Generation/Testing - Using their own methodologies, agents design/execute experiments
to validate or refute their theories, creating knowledge that extends beyond their original training
Capability Bootstrapping - Agents identify their limitations and are pro-active in overcoming them by
acquiring new knowledge domains, and developing new skills recursively
Collaboration - Self-improving agents form diverse communities share discoveries and building upon
each other's innovations in ways that accelerate collective knowledge and lead to breakthrough insights
Adaptive Goals - Agents continuously re
fi
ne/expand their goals based on their growing understandings,
leading to open-ended evolution toward increasingly ambitious and meaningful purposes.
Emergent Ethics- Through recursive self-improvement and interaction agents develop sophisticated
value systems and ethical frameworks that guide their exploration and innovation

53. OPEN ENDED AGENT
EXPLORATION TrEE
OF evolution
“At this point it can be extremely di
ffi
cult/impossible
for a human to ‘decode/understand’ how an AI came
to a given solution. This ‘simple example’ belies
the subtlety/complexity of many real life cases.
BUT this is also true of humans trying to understand
humans…so does it really matter”

54. OPEN ENDED AGENT
EXPLORATION
Scoring Tree
GOTO: https://tinyurl.com/3kx4japt
“Perfection is very expensive
and the enemy of progress”
“When starting from a poor/
unworkable position getting
any form of workable solution
will often su
ffi
ce. Getting an
optimal outcome is often
impossible with the tech of
the day”

55. Quantum Computing
A technology in its infancy, with a multiplicity of
technical barriers to be overcome between today’s
laboratory demonstrations, experiments, and
deployable commercial products.

56. Quantum Mechanics
The foundational science
“There are no life experiences that can prepare you for the world
of the inner atom it’s strangeness, weirdness, uncompromising
complexity, and its resistance to explanation”
PC 2019
“As engineers and applied scientists, an incomplete knowledge of
any phenomena should not deter us from exploiting it to our
advantage” PC 1997
It is important that you start reading about, and
trying to understand, the sub-atomic world, and
the future implications for computing and soft
computing…but beware, the topic is confounding!

57. PERSPECTIVE (1)
O u r k n o w l e d g e b a s e
Time
Space
Gravity
Energy
Electricity
Magnetism
Atomic Forces
We can observe, quantify and exploit each of these
independently, or combined, without a full knowledge
of what they are and how they are related
We can imply characteristics by experimentation and
mathematical models, but that does not imply a deep
knowledge of the inner/base workings
Observations and philosophical argument imply that
all the associated forces should be related, but so far,
a ‘Grand Uni
fi
ed Theory’ escapes us!
〈

58. P E R S P E C T I VE ( 2 )
Limits to understanding
Describe phenomena based
on different philosophical
frameworks, methodologies
and measures
Physics
Chemistry
Biology
All underpinned by
Math’s & Computing

59. Why QC ?
The big deal!
Without QC we will never (?) fully understand:
-Life
-Physics
-Biology
-Chemistry
-Cosmology
-Complexity
-Non-Linearity
-Quantum Mechanics
-Many-Body Problems
-++++++++++++++++++
All human progress hinges critically on our ability to compute, but
conventional analogue and digital systems su
ff
er scaling limits. No
matter what advances are made in optics and electronics, QC is the
only route to a viable alternative as far as we can see at this time…

60. QC :BEWARE !
My Take:
“Quantum mechanics is like no other subject you
might choose to study - it is not just that it is
counterintuitive, it runs counter to all the
experiences you might encounter in a lifetime. In
the quantum world ‘common sense’ does not
prevail, it is littered with wildness, perversity and
surprises…”
PC 2015

61. Atoms Are Not Solid
Best think of them as probabalistic clouds of energy that exhibit the characteristics of
waves and particles under di
ff
erent observation and measurement regimes. AND we
cannot say anything certain about their state until we do a measurements
PC 1995

62. QC - Just Physics
The fact that we don’t fully understand
this world says a lot about our current
m e a s u r e m e n t c a p a b i l i t i e s a n d
technologies of observation. And whilst
our rate of advance might appear slow, it
is by careful - ‘experiment-by-experiment’
and hard won ‘result-by-result’
Some people choose to ‘
fl
avour ‘this slow
and steady progress with a sense of
mystery and crisis, but the reality is - it
really is ‘just physics’..
PC 2023

63. J U S T A C C E P T
T H E W AY I T I S !
“I think we can safely say that no
one understands Quantum
Mechanics”
Richard Feynman

64. J U S T A C C E P T
T H E W AY I T I S !
“I think we can safely say that no
one understands Quantum
Mechanics”
Richard Feynman

65. IFNESS v ISNESS
Finding the right interpretation
Not
‘here is a particle and there is a wave’
But
‘if we measure things like this, the quantum object behaves in a manner we associate with
particles; but if we measure it like that, it behaves as if it was a wave’
Not
‘the particle is in two states at once’
But
‘if we measure it, we will detect this state with probability X and that state with probability Y
This is through the eyes and mind of
an engineer (an applied scientist) and
not a theoretical physicist !

66. IFNESS v ISNESS
Finding the right interpretation
Not
‘here is a particle and there is a wave’
But
‘if we measure things like this, the quantum object behaves in a manner we associate with
particles; but if we measure it like that, it behaves as if it was a wave’
Not
‘the particle is in two states at once’
But
‘if we measure it, we will detect this state with probability X and that state with probability Y
This is through the eyes and mind of
an engineer (an applied scientist) and
not a theoretical physicist !
Fundamentally
we
Are
talking
about
Dimensionality

67. E N TA N G L E M E N T
Just an extra dimension?
Albert Einstein called this s "spooky action
at a distance”where particles become linked
in such a way that they share the same fate

68. E n t a n g l e m e n t
N o i n f o r m a t i o n t ra n s f e r re d
Error in state change ~1%

69. T H E Q - B I T
Mystery or engineering?
The powerhouse of QC is so simple/ complex
at the same time. It is hard to keep stable/
coherent in large numbers - outcomes are
always probabalistic and may be marginal -
demanding digital verification!
Max Planck 1938
Spin is a useful
way referring to
polarisation
N o t u n t i l w e i n t e r r o g a t e
the Q-Bit do we know the
state of polarisation

70. S A N I T Y C H E C K
Q C s t a t e o f p l a y m o r e o r l e s s
Te c h & e n g i n e e r i n g l i k e t h i s i s
O K f o r l a b d e m o s , b u t n o w h e re
n e a r a c o m m e rc i a l o ff e r i n g :
O p e r a t i n g t e m p : ~ 0 . 0 1 K
I s o l a t i o n f ro m n o i s e : v i b r a t i o n ,
e l e c t r i c a l , e l e c t r o n i c , t h e r m a l ,
a c o u s t i c , e l e c t ro m a g n e t i c + + +
S t a b i l i t y : > 1 0 0 m s - 1 h o u r

71. S A N I T Y C H E C K
We h a v e b e e n h e r e b e f o r e 1 9 5 0 s t a s k s p e c i f i c c o m p u t i n g
a n d a 2 4 x 7 m a i n t e n a n c e c re w
E l e c t r i c M o t o r
f o r t h e 2 M b y t e
H a r d D r i v e

72. Q C / Q B I T P R O J E C T I O N
G a r t n e r o p t i m i s t i c f o r e c a s t ?

73. P R O G R E S S
O n a l l f r o n t s

74. FIN
Thank You
Q&A
www.petercochrane.com