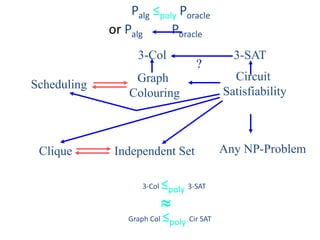
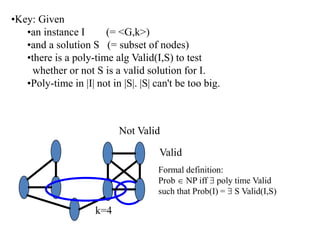
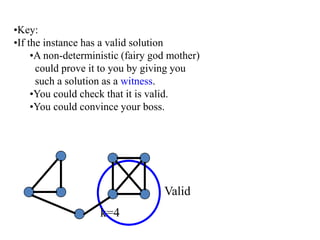
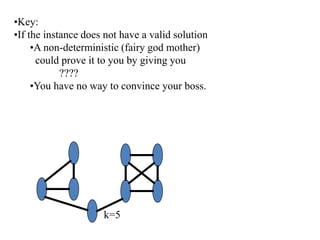
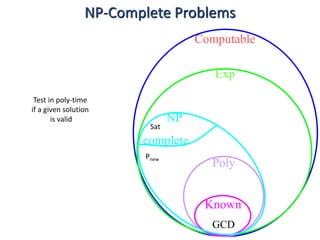
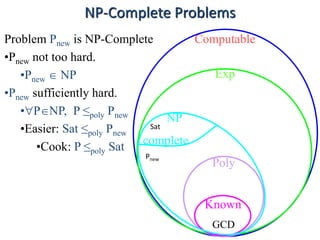
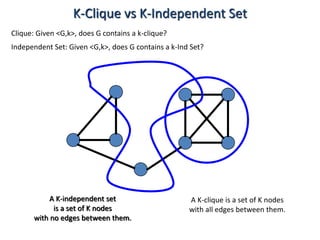
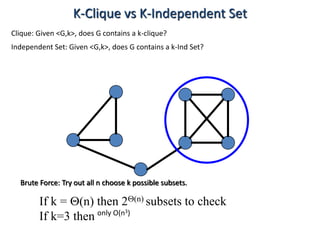
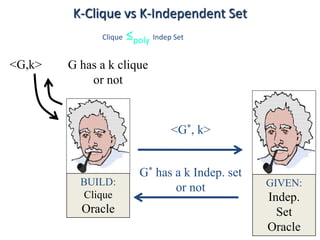
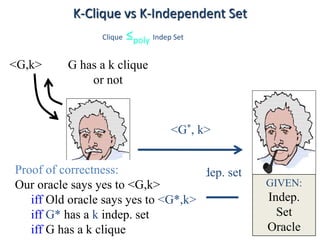
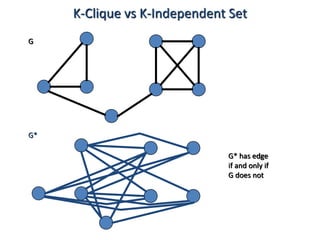
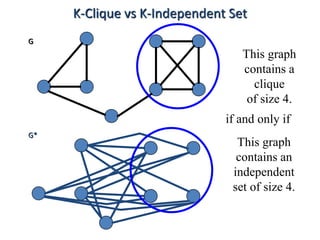
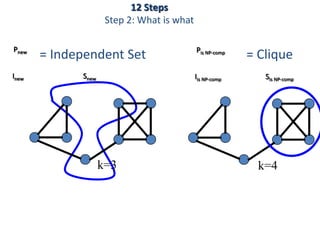
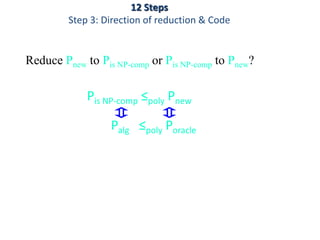
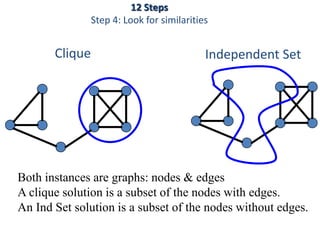
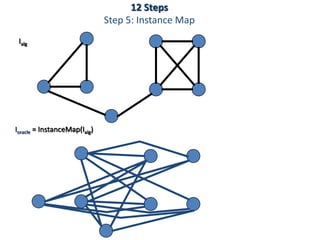
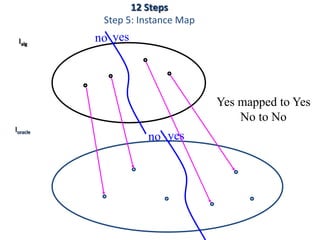
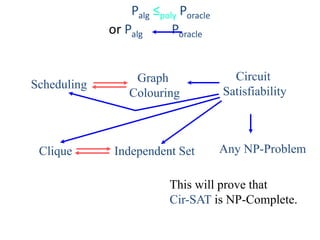
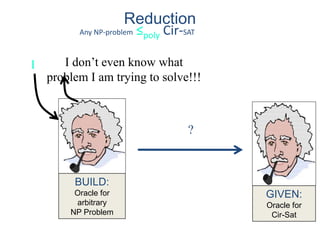
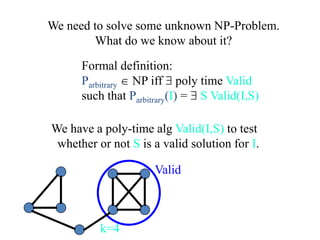
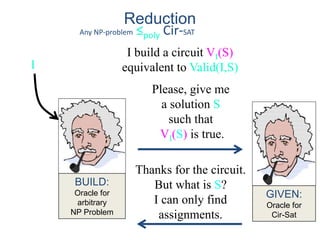
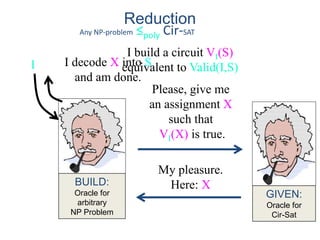
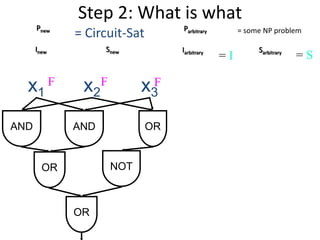
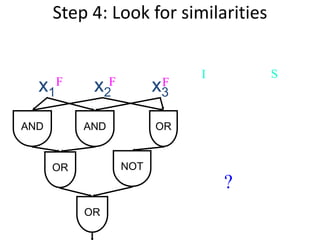
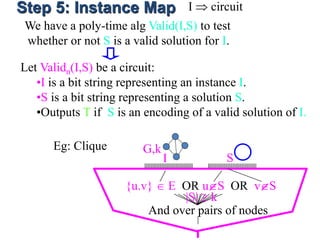
This document discusses dynamic programming algorithms and NP-completeness. It begins by outlining 12 steps for proving that a new problem Pnew is NP-complete. It then provides examples of reducing the clique problem to the independent set problem to show they are equivalent. The document explains the concepts of instances, solutions, validity and reductions. It shows how to reduce any NP problem to the circuit satisfiability problem by building a circuit VI(S) that is equivalent to checking if a solution S is valid for a given instance I.

2. UNIT III
DYNAMIC PROGRAMMING ALGORITHMS
Developing a Dynamic Programming Algorithm-Subtle Points- Question for
the Little Bird- Sub instances and Sub solutions-Set of Substances-
Decreasing Time and Space-Number of Solutions-Code. Reductions and NP-
Completeness-Satisfiability-Proving NP-Completeness- 3-Coloring- Bipartite
Matching. Randomized Algorithms-Randomness to Hide Worst Cases-
Optimization Problems with a Random Structure.

3. Dynamic Programming
• A hard topic.
• I try to provide a unified way to think of it
and a fixed set of steps to follow.
• Even if you don’t get the details of the
algorithm correct, at least get the right structure.
• I provide analogies (little bird) to make it
hopefully more fun & easier to follow.

4. •An optimization problem
•Each solution is either valid or not
(no cost)
•The output is
•Yes, it has a valid solution.
•No, it does not
•the solution is not returned
•Eg: Given graph and integer <G,k>,
does G have a clique of size k?
Non-Deterministic
Poly-Time Decision Problems (NP)

5. •Key: Given
•an instance I (= <G,k>)
•and a solution S (= subset of nodes)
•there is a poly-time alg Valid(I,S) to test
whether or not S is a valid solution for I.
•Poly-time in |I| not in |S|. |S| can't be too big.
k=4
Valid
Not Valid
Formal definition:
Prob  NP iff  poly time Valid
such that Prob(I) =  S Valid(I,S)

6. •Key:
•If the instance has a valid solution
•A non-deterministic (fairy god mother)
could prove it to you by giving you
such a solution as a witness.
•You could check that it is valid.
•You could convince your boss.
k=4
Valid

7. •Key:
•If the instance does not have a valid solution
•A non-deterministic (fairy god mother)
could prove it to you by giving you
????
•You have no way to convince your boss.
k=5

8. •Example: 3-Col:
•Instance: A graph G.
•Solution: Colouring C nodes of G with
3 colours such that every edge has two
colours.
•G is a Yes instance if there is such a
colouring.
•Given an instance G and a solution C,
there is a poly-time alg Valid(G,C) to
test whether or not C is a valid 3-
colouring
of G.
 3-Col  NP.
Non-Deterministic Poly-Time (NP)

9. •Example: Airplane Wing:
•Instance: Requirements I of the wing.
•Solution: A description S of how to make the wing.
•I is a Yes instance if there is such a wing.
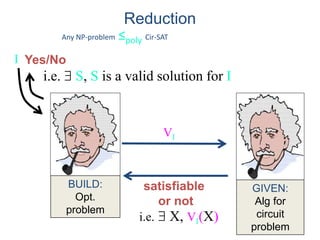
•Given an instance I and a proof S,
there is a poly-time alg Valid(I,S) to test
whether or not S is a valid solution for I.
Airplane Wing  NP.
I = [weight, lift, cost, …]
Non-Deterministic Poly-Time (NP)

10. Reductions
•Reduction: Design a fast algorithm for one computational problem,
using a supposedly fast algorithm for another problem as a
subroutine.
Palg ≤poly Poracle

11. • Definition is asymmetric.
• There is a witness that a graph has a 3-Col.
• There is no known witness that a graph has no 3-Col.
Cook Reduction:
• Design any fast algorithm for Palg using a supposed fast
algorithm for Poracle as a subroutine.
Karp Reduction:
The algorithm for Palg calls that for Poracle only once
Yes  Yes & No  No
NP vs Co-NP Preserving Reductions

12. We will only consider reductions of this simple form. Because they preserve NP
vs Co-NP
Karp Reduction:
Yes  Yes
& No  No

13. • Problem Pnew is NP-Complete
• Pnew not too hard.
• Pnew  NP

14. Computable
Exp
Poly
Known
GCD
NP
complete
NP-Complete Problems
Pnew
Test in poly-time
if a given solution
is valid
Sat

15. Computable
Exp
Poly
Known
GCD
NP
complete
NP-Complete Problems
Problem Pnew is NP-Complete
•Pnew not too hard.
•Pnew  NP
•Pnew sufficiently hard.
•PNP, P ≤poly Pnew
•Easier: Sat ≤poly Pnew
•Cook: P ≤poly Sat
Pnew
Sat

16. Clique: Given <G,k>, does G contains a k-clique?
A K-independent set
is a set of K nodes
with no edges between them.
Independent Set: Given <G,k>, does G contains a k-Ind Set?
K-Clique vs K-Independent Set
A K-clique is a set of K nodes
with all edges between them.

17. Clique: Given <G,k>, does G contains a k-clique?
Independent Set: Given <G,k>, does G contains a k-Ind Set?
K-Clique vs K-Independent Set
Brute Force: Try out all n choose k possible subsets.
If k = (n) then 2(n) subsets to check
If k=3 then only O(n3)

18. GIVEN:
Indep.
Set
Oracle
<G,k>
BUILD:
Clique
Oracle
<G*, k>
G* has a k Indep. set
or not
G has a k clique
or not
Clique ≤poly Indep Set
K-Clique vs K-Independent Set

19. GIVEN:
Indep.
Set
Oracle
<G,k>
BUILD:
Clique
Oracle
<G*, k>
G* has a k Indep. set
or not
G has a k clique
or not
Clique ≤poly Indep Set
Proof of correctness:
Our oracle says yes to <G,k>
iff Old oracle says yes to <G*,k>
iff G* has a k indep. set
iff G has a k clique
K-Clique vs K-Independent Set

20. G*
G
G* has edge
if and only if
G does not
K-Clique vs K-Independent Set

21. G*
G
This graph
contains a
clique
of size 4.
This graph
contains an
independent
set of size 4.
if and only if
K-Clique vs K-Independent Set

22. •Steps for proving that Pnew is NP-Complete
• 1) I am addicted to solving NP-Complete Problems
• 2) I trust in my higher power to help
A witness
12 Steps

23. •Steps for proving that Pnew is NP-Complete
• 0) Pnew  NP
• 1) What to reduce it to
2) What is what
3) Direction of reduction & Code
4) Look for similarities
5) Instance Map
6) Solution Map
7) Valid to Valid
8) Reverse Solution Map
9) Valid to Valid
10) Working Algorithm
11) Running Time
12 Steps

24. Formal definition:
Pnew  NP iff  poly time Valid
such that Pnew(I) =  S Valid(I,S)
•Design poly-time algorithm Valid(I,S)
•which determines whether a given solution S
•is valid for a given instance I.
12 Steps
Step 0: Pnew  NP

25. Palg ≤poly Poracle
Choose a problem Pis NP-comp
that is as similar to Pnew as possible and
that is already known to be NP-Complete.
12 Steps
Step 1: What to reduce it to

26. = Independent Set = CliquePnew Pis NP-comp
Inew Iis NP-comp
k=4k=3
Snew Sis NP-comp
12 Steps
Step 2: What is what

27. Reduce Pnew to Pis NP-comp or Pis NP-comp to Pnew?
Pis NP-comp ≤poly Pnew
Palg ≤poly Poracle
12 Steps
Step 3: Direction of reduction & Code

28. 12 Steps
Step 3: Direction of reduction & Code

29. Independent SetClique
Both instances are graphs: nodes & edges
A clique solution is a subset of the nodes with edges.
An Ind Set solution is a subset of the nodes without edges.
12 Steps
Step 4: Look for similarities

30. 12 Steps
Step 5: Instance Map

31. Ioracle = InstanceMap(Ialg)
Ialg
12 Steps
Step 5: Instance Map

32. Ioracle
Ialg
no yes
no yes
Yes mapped to Yes
No to No
12 Steps
Step 5: Instance Map

33. 12 Steps
Step 6: Solution Map

34. Ioracle
Ialg
Potential Solution S.
Potential Solution
= SolutionMap(S).
12 Steps
Step 6: Solution Map

35. Salg = SolutionMap(Soracle)
Ioracle = InstanceMap(Ialg)
Ialg
Soracle
If Soracle is valid
solution for Ioracle,
then Salg is valid
solution for Ialg
Valid
Valid
12 Steps
Step 7: Valid to Valid

36. Ioracle
Ialg
Potential Solution S.
Potential Solution
= ReverseSolutionMap(S).
12 Steps
Step 8: Reverse Solution Map
Not part of code,
but of proof.

37. Salg
Ioracle = InstanceMap(Ialg)
Ialg
Soracle = ReverseSolutionMap(Salg)
If Salg is valid
solution for Ialg,
then Soracle is valid
solution for Ioracle
Valid
Valid
12 Steps
Step 9: Valid to Valid

38. Our Algalg says yes to Ialg
iff old Algoracle says yes to Ioracle
iff Ioracle has a valid solution Soracle
iff Ialg has a valid solution Salg
iff Ialg is a yes instance.
Steps 6&7Steps 8&9
12 Steps
Step 10: Working Algorithm

39. Salg = SolutionMap(Soracle)
Ioracle = InstanceMap(Ialg)
Algalg(Ialg) is poly time if
the following are poly time:
Algoracle(Ioracle)
Assumed
Your job
12 Steps
Step 11: Running Time

40. Graph
Colouring
Scheduling
Clique Independent Set
Palg ≤poly Poracle
or Palg Poracle
Circuit
Satisfiability
Any NP-Problem
This will prove that
Cir-SAT is NP-Complete.

41. GIVEN:
Oracle for
Cir-Sat
I
BUILD:
Oracle for
arbitrary
NP Problem
?
I don’t even know what
problem I am trying to solve!!!
Reduction
Any NP-problem ≤poly Cir-SAT

42. We have a poly-time alg Valid(I,S) to test
whether or not S is a valid solution for I.
k=4
Valid
Formal definition:
Parbitrary  NP iff  poly time Valid
such that Parbitrary(I) =  S Valid(I,S)
We need to solve some unknown NP-Problem.
What do we know about it?

43. GIVEN:
Oracle for
Cir-Sat
I
BUILD:
Oracle for
arbitrary
NP Problem
Please, give me
a solution S
such that
Valid(I,S) is true.
Reduction
Any NP-problem ≤poly Cir-SAT
That looks like
a Turing Machine.
I only know about
circuits

44. The Circuit Satisfiability Problem
x3x2x1
OR
ORANDAND
OR
NOT
One bit output
No feedback
An instance is a circuit C.
F T F
A solution is an assignment X = [F,T,F…].
F F
F F
T
C(X) evaluates to T or F.

45. The Circuit Satisfiability Problem
x3x2x1
OR
ORANDAND
OR
NOT
An instance is a circuit C.
A solution is an assignment X = [F,T,F…].
A valid solution has C(X) = True.
F F F
F F
F T
F
Given a circuit,
does it have a
satisfying assignment?

46. Very Powerful
Turing (and friends) prove that
any algorithm computed by a
JAVA program in poly-time
can be computed by a
Turing Machine in poly-time.
Cook proves that any algorithm
computed by a Turing Machine
in time T(n) can be computed
by a family of circuits of size [T(n)]2.
But clearly, circuits compute.
The Circuit Satisfiability Problem

47. GIVEN:
Oracle for
Cir-Sat
I
BUILD:
Oracle for
arbitrary
NP Problem
Please, give me
a solution S
such that
VI(S) is true.
Reduction
Any NP-problem ≤poly Cir-SAT
Thanks for the circuit.
But what is S?
I can only find
assignments.
I build a circuit VI(S)
equivalent to Valid(I,S)

48. GIVEN:
Oracle for
Cir-Sat
I
BUILD:
Oracle for
arbitrary
NP Problem
Please, give me
an assignment X
such that
VI(X) is true.
Reduction
Any NP-problem ≤poly Cir-SAT
My pleasure.
Here: X
I build a circuit VI(S)
equivalent to Valid(I,S)I decode X into S
and am done.

49. 12 Step Program
•Let's be more formal.
•And flow the 12 steps.

50. Step 0: Cir-SAT  NP
•Design poly-time algorithm ValidCir-SAT(C,X)
•which determines whether a given assignment X
•is valid for a given circuit C.
• Easy: Evaluate C(X).

51. Step 1: What to reduce it to
Palg ≤poly Cir-Sat
Choose a problem Pis NP-comp
that is as similar to Cir-Sat as possible and
that is already known to be NP-Complete.
Any NP-problem ≤poly Cir-SAT
Have none.
We have a poly-time alg Valid(I,S) to test
whether or not S is a valid solution for I.

52. Step 2: What is what
= Circuit-Sat = some NP problemPnew Parbitrary
Inew IarbitrarySnew Sarbitrary
= I = S
x3x2x1
OR
ORANDAND
OR
NOT
F F F

53. Step 3: Direction of reduction & Code
Given oracle for Cir-Sat,
we need to be able to solve any NP-Complete problem.
Cir-Sat
Parbitrary

54. I S
x3x2x1
OR
ORANDAND
OR
NOT
F F F
Step 4: Look for similarities
?

55. Step 5: Instance Map

56. Step 5: Instance Map I  circuit
We have a poly-time alg Valid(I,S) to test
whether or not S is a valid solution for I.
Let Validn(I,S) be a circuit:
•I is a bit string representing an instance I.
•S is a bit string representing a solution S.
•Outputs T if S is an encoding of a valid solution of I.
I S
G,k
And over pairs of nodes
{u.v}  E OR uS OR vS
Eg: Clique
|S|  k

57. Step 5: Instance Map
Outputs T if
S is an encoding of
a valid solution S of I
I S
I  circuit
hard wired
Given an instance I
Circuit VI(S) = Valid(I,S)
Validn(I,S)
I VI(S)

58. Step 6: Solution Map

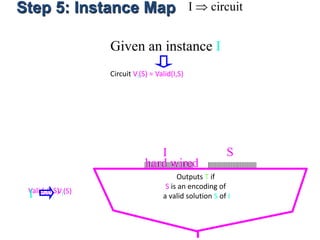
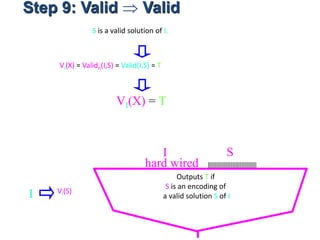
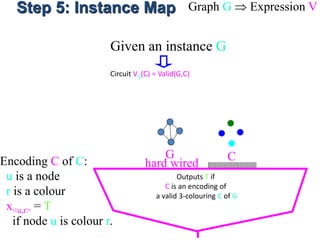
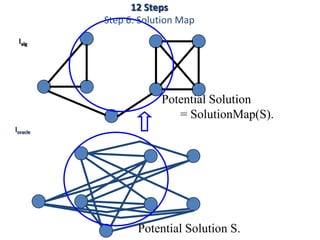
59. Step 6: Solution Map S  assignment
X is viewed as a bit string S representing a solution S.
If X is not a bit string
representing a solution
then “what ever”
X=[T,F,F,T,F,T]
Outputs T if
S is an encoding of
a valid solution S of I
I S
hard wired
I VI(S)

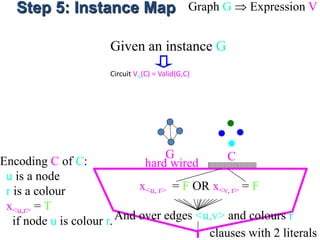
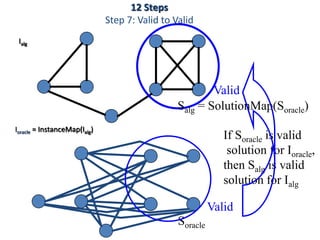
60. Step 6: Solution Map S  assignment
X is viewed as a bit string S representing a solution S.
X=[T,F,F,T,F,T]
Outputs T if
S is an encoding of
a valid solution S of I
I S
hard wired
I VI(S)
solution S

61. Step 7: Valid  Valid
VI(X) = T
Outputs T if
S is an encoding of
a valid solution S of I
I S
hard wired
I VI(S)
Valid(I,S) = Validn(I,S) = VI(X) = T
S is a valid solution of I.

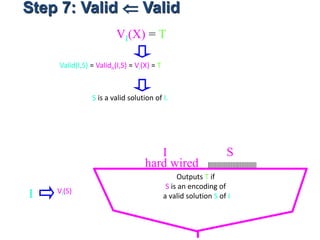
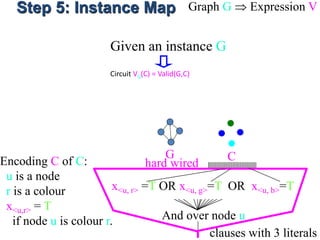
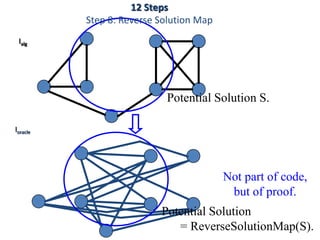
62. Step 8: Rev. Sol. Map solution  assignment
S bit string representing a solution S
solution S
X=[T,F,F,T,F,T]
Outputs T if
S is an encoding of
a valid solution S of I
I S
hard wired
I VI(S)

63. Step 9: Valid  Valid
Outputs T if
S is an encoding of
a valid solution S of I
I S
hard wired
I VI(S)
S is a valid solution of I.
VI(X) = T
VI(X) = Validn(I,S) = Valid(I,S) = T

64. GIVEN:
Alg for
circuit
problem
BUILD:
Opt.
problem
I
satisfiable
or not
Yes/No
Reduction
VI
i.e.  S, S is a valid solution for I
i.e.  X, VI(X)
Any NP-problem ≤poly Cir-SAT

65. Graph
Colouring
Scheduling
Clique Independent Set
Palg ≤poly Poracle
or Palg Poracle
Circuit
Satisfiability
Any NP-Problem
3-Col
?

66. 3-Col
Graph Col: Given graph G & k
can G be coloured with k colours?
3-Col: Given graph G
can G be coloured with 3 colours?
3-Col ≤poly Graph Col
If you can decide whether you can colour with k colours,
then you can decide whether you can colour with 3 colours.
G,k C CG

67. Graph
Colouring
Scheduling
Clique Independent Set
Palg ≤poly Poracle
or Palg Poracle
Circuit
Satisfiability
Any NP-Problem
3-Col 3-SAT
?

68. 3-SAT
Cir Sat: Given circuit C
does it have a satisfying assignment X?
3-SAT: Given an expression:
•A circuit consisting of a big AND of clauses
•Each clause is the OR of at most 3 literals
•Each literal is a variable or its negation.
does it have a satisfying assignment X?
xoryorz AND xorwora AND …
F T TF F F F T TF F F

69. 3-SAT
Cir Sat: Given circuit C
does it have a satisfying assignment X?
3-SAT: Given an expression:
does it have a satisfying assignment X?
xoryorz AND xorwora AND …
F T TF F F F T TF F F
3-Sat ≤poly Cir Sat
If you can decide whether any circuit is satifiable,
then you can decide whether a circuit that happens to be
an expression is satisfiable.

70. Graph
Colouring
Scheduling
Clique Independent Set
Palg ≤poly Poracle
or Palg Poracle
Circuit
Satisfiability
Any NP-Problem
3-SAT3-Col
?
Graph Col ≤poly Cir SAT

3-Col ≤poly 3-SAT

71. Step 5: Instance Map Graph G  Expression V
Given an instance G
Circuit VG(C) = Valid(G,C)
G
Outputs T if
C is an encoding of
a valid 3-colouring C of G
hard wired
CEncoding C of C:
u is a node
r is a colour
x<u,r> = T
if node u is colour r.

72. Step 5: Instance Map Graph G  Expression V
Given an instance G
Circuit VG(C) = Valid(G,C)
G
hard wired
CEncoding C of C:
u is a node
r is a colour
x<u,r> = T
if node u is colour r.And over edges <u,v> and colours r
x<u, r> = F OR x<v, r> = F
clauses with 2 literals

73. Step 5: Instance Map Graph G  Expression V
Given an instance G
Circuit VG(C) = Valid(G,C)
G
hard wired
CEncoding C of C:
u is a node
r is a colour
x<u,r> = T
if node u is colour r. And over node u
clauses with 3 literals
x<u, r> =T OR x<u, g>=T OR x<u, b>=T