This document is the teacher's guide for the Grade 10 Mathematics curriculum developed by the Department of Education of the Philippines. It provides teachers with guidelines for effectively teaching the content to help students attain the expected learning competencies and standards. The teacher's guide includes learning outcomes, assessment plans, lesson plans, activities with answers, practice tests and references to help teachers deliver creative and engaging mathematics instruction. It aims to equip teachers with the necessary resources to teach the lessons in an interactive and effective manner.
































![D
EPED
C
O
PY
106
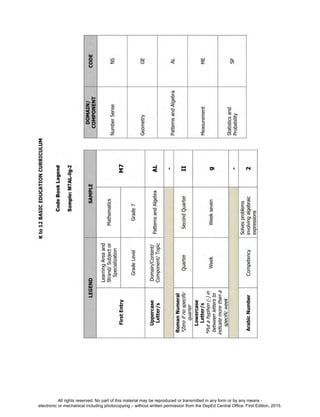
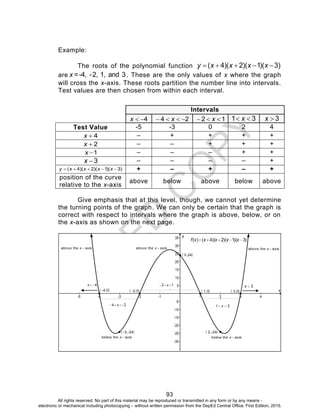
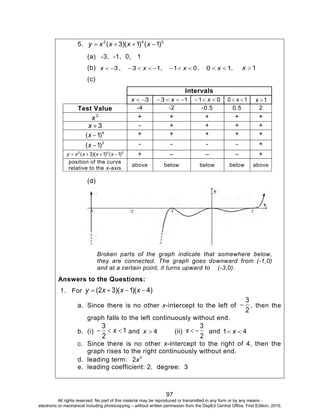
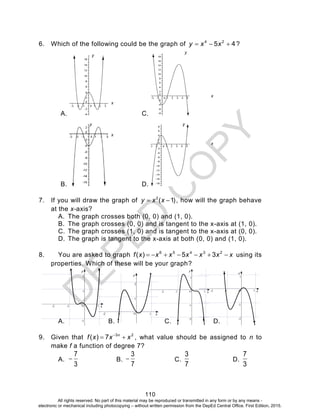
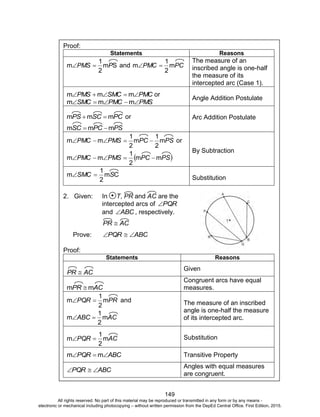
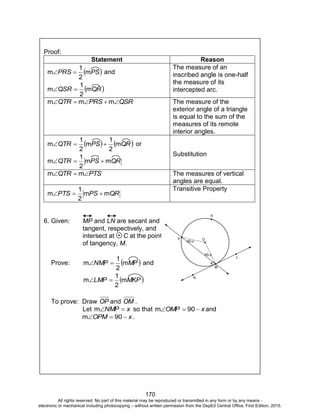
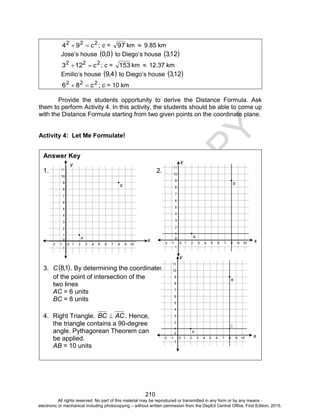
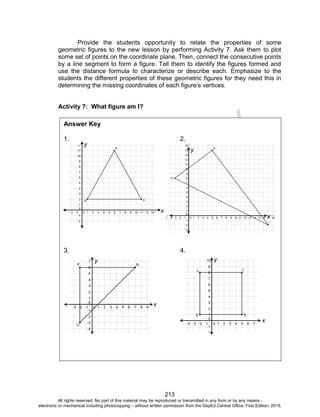
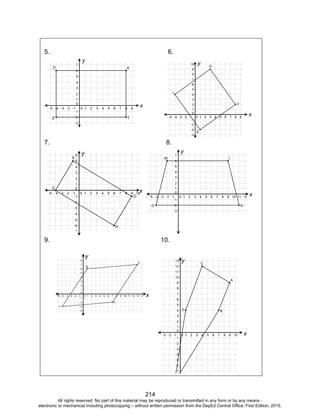
Activity 13: Investigate Deeper and Decide Wisely
Answers to the Questions
1. a. 50%
b. The value given by the table is 23.7%. The polynomial gives a
value of 26.3%. The given polynomial is the cubic polynomial
that best fits the data. We expect it to give a good
approximation of the forest cover but it may not necessarily
produce the exact values.
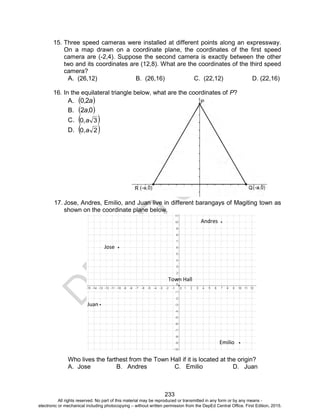
c. The domain of the function is [0,98]. Since year 2100
corresponds to x = 200, we cannot use the function to predict
forest cover during this year. Moreover, if x = 200, the
polynomial predicts a forest cover of 59.46%. This is very
unrealistic unless major actions are done to reverse the trend.
You can find other data that can be modelled by a
polynomial. Use the regression tool in MS Excel or GeoGebra
to determine the best fit polynomial for the data.
2. The figure below can help solve the problem.
18 - 2x18
24 - 2x
24
x
x
x
x
x
x
x
x
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2015.](https://image.slidesharecdn.com/math10tgu2-160922005022/85/Math10-tg-u2-45-320.jpg)































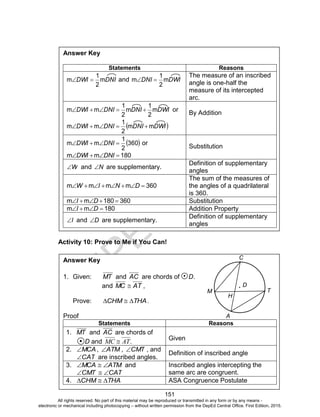





































































![D
EPED
C
O
PY
237
Score Descriptors
misinterprets less significant ideas or details.
2
Poses a problem and finishes some significant parts of the
solution and communicates ideas unmistakably but shows
gaps on theoretical comprehension.
1
Poses a problem but demonstrates minor comprehension, not
being able to develop an approach.
Source: D.O. #73, s. 2012
Glossary of Terms
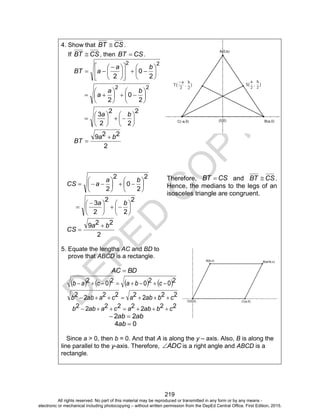
Coordinate Proof – a proof that uses figures on a coordinate plane to prove
geometric relationships.
Distance Formula – an equation that can be used to find the distance between
any pair of points on the coordinate plane. The distance formula is
2
12
2
12 yyxxd or 2
12
2
12 yyxxPQ , if 11 y,xP and
22 y,xQ are points on a coordinate plane.
Horizontal Distance (between two points) – the absolute value of the difference
of the x-coordinates of two points
Midpoint – a point on a line segment that divides the same segment into two
equal parts.
Midpoint Formula – a formula that can be used to find the coordinates of the
midpoint of a line segment on the coordinate plane. The midpoint of 11 y,xP
and 22 y,xQ is
22
2121 yy
,
xx
.
Answer Key
Part I Part II (Use the rubric to rate students’ works/outputs)
1. C 11. A 1. 556 km
2. C 12. B 2. 15 km
3. C 13. C
4. A 14. B
5. B 15. A Part III A (Use the rubric to rate students’ works/outputs)
6. D 16. C Part III B (Use the rubric to rate students’ works/outputs)
7. D 17. C
8. B 18. C
9. B 19. C
]10. D 20. C
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2015.](https://image.slidesharecdn.com/math10tgu2-160922005022/85/Math10-tg-u2-176-320.jpg)



![D
EPED
C
O
PY
241
Khan Academy. Equation for a circle using the Pythagorean Theorem. Retrieved
from https://www.khanacademy.org/math/geometry/ cc-geometry-
circles/equation-of-a-circle/v/equation-for-a-circle-using-the-pythagorean-theorem
Ukmathsteacher. Core 1 – Coordinate Geometry (3) – Midpoint and distance
formula and Length of Line Segment. Retrieved from
http://www.youtube.com/watch?v=qTliFzj4wuc
VividMaths.com. Distance Formula. Retrieved from
http://www.youtube.com/watch?v=QPIWrQyeuYw
Website Links for Images:
asiatravel.com. Pangasinan Map. Retrieved from
http://www.asiatravel.com/philippines/pangasinan/pangasinanmap.jpg
DownTheRoad.org. Pictures of, Chengdu to Kangding, China Photo, Images,
Picture from. (2005). Retrieved from http://www.downtheroad.org/Asia/Photo/
9Sichuan_China_Image/3Chengdu_Kangding_China.htm
funcheap.com. globe-map-wallpapers_5921_1600[1]. Retrieved from
http://sf.funcheap.com/hostelling-internationals-world-travel-101-santa-
clara/globe-map-wallpapers_5921_16001/
Hugh Odom Vertical Consultants. eleven40 theme on Genesis Framework·
WordPress. Cell Tower Development – How Are Cell Tower Locations Selected?
Retrieved from http://blog.thebrokerlist.com/cell-tower-development-how-are-cell-
tower-locations-selected/
LiveViewGPS, Inc. GPS Tracking PT-10 Series. (2014). Retrieved from
http://www.liveviewgps.com/gps+tracking+device+pt-10+series.html
Sloan, Chris. Current "1991" Air Traffic Control Tower at Amsterdam Schiphol
Airport – 2012. (2012). Retrieved from http://airchive.com/html/airplanes-and-
airports/amsterdam-schipol-airport-the-netherlands-/current-1991-air-traffic-
control-tower-at-amsterdam-schiphol-airport-2012-/25510
wordfromthewell.com. Your Mind is Like an Airplane. (2012). Retrieved from
http://wordfromthewell.com/2012/11/14/your-mind-is-like-an-airplane/
All rights reserved. No part of this material may be reproduced or transmitted in any form or by any means -
electronic or mechanical including photocopying – without written permission from the DepEd Central Office. First Edition, 2015.](https://image.slidesharecdn.com/math10tgu2-160922005022/85/Math10-tg-u2-180-320.jpg)