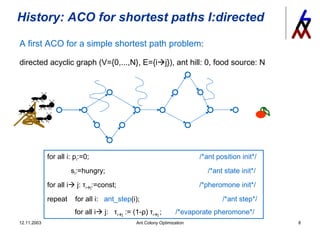
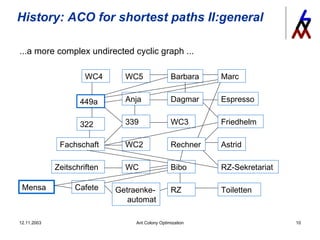
The document discusses ant colony optimization (ACO), a metaheuristic optimization algorithm inspired by the behavior of ants. It provides examples of how ACO has been applied to solve shortest path problems, the traveling salesperson problem, and protein folding. It also notes that ACO is a robust method applicable to general non-static optimization problems and has achieved state-of-the-art results for some problems when combined with local search techniques and elitism in pheromone updates.

1. Ameisenalgorithmen – Ant Colony Optimization Lehrprobe zur Habilation, Barbara Hammer, AG LNM, Universität Osnabrück

2. Optimization Given a graph with two specified vertices A and B, find a shortest path from A to B. Given a set of cities and pairwise distances, find a shortest tour. Given a sequence of amino acids of a protein, find the structure of the protein. ‘ Where is my manuscript for the talk, I put it on this pile of papers...’ General optimization problem: given f:X  ℝ, find x ε X such that f(x) is minimum  needle in a haystack, hopeless  traveling salesperson problem, NP-hard  shortest path problem, polynomial  protein structure prediction problem, NP-hard

3. Ant colony food nest

4. Ant Colony Optimization (ACO): a heuristic optimization method for shortest path and other optimization problems which borrows ideas from biological ants

5. Ant Colony Optimization Outline History: ACO for shortest paths Traveling salesperson and ACO-metaheuristic Protein folding - state of the art ACO General comments - where is my manuscript?

6. History: ACO for shortest paths …

7. History: ACO for shortest paths Goss et al. 1989, Deneuborg et al. 1990 experiments with Argentine ants: ants go from the nest to the food source and backwards after a while, the ants prefer the shortest path from the nest to the food source stigmercy : the ants communicate indirectly laying pheromone trails and following trails with higher pheromone length gradient  pheromone will accumulate on the shortest path Dorigo et al. 1991 applications to shortest path problems nest food

8. History: ACO for shortest paths I:directed A first ACO for a simple shortest path problem : directed acyclic graph (V={0,...,N}, E={i  j}), ant hill: 0, food source: N for all i: p i :=0; /*ant position init*/ s i :=hungry; /*ant state init*/ for all i  j: τ i  j :=const; /*pheromone init*/ repeat for all i: ant_step (i); /*ant step*/ for all i  j: τ i  j := (1- ρ ) τ i  j ; /*evaporate pheromone*/

9. History: ACO for shortest paths I:directed ant_step (i): if p i =N: s i :=satisfied; if p i =0: s i :=hungry; /*collect food/deliver food*/ if s i =hungry: choose j with p i  j with probability τ pi  j / Σ pi  j’ τ pi  j’ /*choose next step*/ update Δτ pi  j := ε ; p i :=j; /*update pheromone*/ if s i =satisfied: choose j with j  p i with probability τ j  pi / Σ j’  pi τ j’  pi update Δτ j  pi := ε ; p i :=j; /* reversed directions*/

10. History: ACO for shortest paths II:general ...a more complex undirected cyclic graph ... WC4 WC5 Barbara Marc 449a Anja Dagmar Espresso 322 339 WC3 Friedhelm Fachschaft WC2 Rechner Astrid Zeitschriften WC Bibo RZ-Sekretariat Toiletten Cafete RZ Getraenke-automat Mensa

11. History: ACO for shortest paths II:general 449a 449a ... Marc was not so happy with the result ...

12. History: ACO for shortest paths II:general for all i: p i :=0; /*ant position init*/ s i :=( ); /*ant brain is empty*/ for all i-j: τ i-j :=const; /*pheromone init*/ repeat for all i: construct_solution (i); for all i: global_pheromone_update (i); for all i-j: τ i-j := (1- ρ ) τ i-j ; /*evaporate*/ construct_solution (i): while p i ≠N /*no solution*/ choose j with p i -j with probability τ pi-j / Σ pi-j’ τ pi-j’ ; p i :=j; append j to s i ; /*remember the trail*/ global_pheromone_update (i): for all j-j’ in s i : Δτ j-j’ := 1/length of the path stored in s i ; minibrain update according to the quality minibrain s i :=hungry repeat for all i: ant_step (i);

13. History: ACO for shortest paths II:general WC4 WC5 Barbara Marc 449a Anja Dagmar Espresso 322 339 WC3 Friedhelm Fachschaft WC2 Rechner Astrid Zeitschriften WC Bibo RZ-Sekretariat Toiletten Cafete RZ Getraenke Mensa

14. History: ACO for shortest paths init pheromone t i-j ; repeat for all ants i: construct_solution (i); for all ants i: global_pheromone_update (i); for all edges: evaporate pheromone; construct_solution (i): init ant; while not yet a solution: expand the solution by one edge probabilistically according to the pheromone; global_pheromone_update (i): for all edges in the solution: increase the pheromone according to the quality ;

15. Traveling salesperson and ACO-metaheuristic …

16. Traveling salesperson Traveling salesperson problem (TSP): given n cities {1,...,N} and distances d ij ≥0 between the cities, find a tour with shortest length, i.e. a permutation π :{1,…,N}  {1,…,N} such that the length = Σ i d π (i) π ((i+1)mod N) is minimum classical NP-hard benchmark problem   A simple greedy heuristic : start somewhere and always add the closest not yet visited city to the tour

17. Traveling salesperson init pheromone; repeat for all ants i: construct_solution (i); for all ants i: global_pheromone_update (i); for all edges: evaporate pheromone; construct_solution (i): init ant; while not yet a solution expand the solution by one edge probabilistically according to the pheromone; global_pheromone_update (i): for all edge in the solution: increase the pheromone according to the quality ; A B C D key observation : a tour (A  C  D  B  A) decomposes into edges A  C, C  D, D  B pheromone on the edges

18. Traveling salesperson init: set τ ij :=const for all cities i≠j; repeat for all ants i: construct_solution (i); for all ants i: global_pheromone_update (i); for all edges i-j: evaporate pheromone;

19. Traveling salesperson global_pheromone_update (i); for all j  k in the solution: Δτ jk := const / length of the constructed tour short tours yield to most pheromone construct_solution (i): set ant to a randomly chosen city; while not yet a solution: j=current city, expand by j  k with probability = only valid tours are constructed close cities are preferred α , β >0 control the mixture of the greedy heuristic and the pheromone following

20. Traveling salesperson Results for a 30 cities instance (10 runs, one hour) Results for larger instances (25000 constructed tours, best tour documented) 25.1 459.8 422 Sim. Annealing 1.5 420.6 420 Tabu-search 1.3 420.4 420 ACO std.deviation average best 21761 21282 100 cities 580 542 545 535 75 cities 443 426 428 425 50 cities Sim.Ann. Evol.Prog. Gen.Alg. ACO

21. ACO-metaheuristic Optimization problem for ACO : over a set of basic components C = {c 1 ,...,c n } partial solutions are subsets s in C feasible (partial) solutions F in C solutions S in C cost function f for solutions Goal : iteratively expand feasible partial solutions by components to reach a solution s with minimum f(s), pheromone attached to each component c i guides the search edges i  j partial tours tours which visit each city at most once and in consecutive order length of the tour valid tours

22. ACO-metaheuristic init pheromone τ i =const for each component c i ; repeat for all ants i: construct_solution (i); for all ants i: global_pheromone_update (i); for all pheromones i: evaporate: τ i =(1- ρ ) ∙τ i ; construct_solution (i); init s={ }; while s is not a solution: choose c j with probability = expand s by c j ; global_pheromone_update (i); for all c j in the solution s: increase pheromone: τ j = τ j + const / f(s); η is a heuristic value, α , β balance the heuristic/pheromone general ACO algorithm

23. Protein folding - state of the art ACO …

24. Protein folding Protein folding given a sequence of amino acids s 1 …s n where s i in {1,0}, i.e. hydrophobic/polar determine the structure of the protein i.e. coordinates in a 2D rectangular lattice, such that neighbored sequence entries are at neighbored positions each position is occupied at most once the number of 1-1 contacts in the 2D structure is maximized in the 2D-HP-model (Dill)

25. Protein folding Dill, 1985 : the HP model preserves important information of the biological conformation Crescenzi et al. and Berger/Leighton, 1998: the problem is NP hard Shmygelska/Hoss, 2003 : ACO 9 additional 1-1 contacts

26. Protein folding start at the left end and iteratively fold one amino acid into a relative direction R,S,R,R,L,L,R,S,R,R,L,R,L,L,R,R,S,R in {R,S,L} length-2 basic components: an element in {i-R,i-S,i-L} represents the local structural motif at position (i-1,i,i+1) pheromone values τ i-D , i = 2.. length-1, D = L,S,R R S R ... R L S

27. Protein folding components : local structural motifs i-D partial solutions : subsets of local structural motifs feasible partial solutions : sequences of consecutive structural motifs without overlap of the amino acids in the 2D lattice solutions : final folds cost function to be maximized: number of 1-1 contacts in the 2D lattice init pheromone τ i-D =const for each tuple i-D ; repeat for all ants i: construct_solution (i); for the best ants i: optimize_solution (i); for the best ants i: global_pheromone_update (i); for all pheromones i-D: evaporate: τ i-D =(1- ρ ) ∙τ i-D ; daemon action: local optimization elitism

28. Protein folding construct_solution (i); init s = { }; while s is not a solution: position j choose a local structural motif j-D with probability proportional to 0 if the position is already occupied or the sequence gets trapped proportional to τ j-D α ∙η j-D β expand s by the chosen motif; η is related to the number of 1-1 contacts of this motif feasibility optimize_solution (i); perform a fixed number of feasible and improving substitutions of local structural motifs at random global_pheromone_update (i); for all local structural motifs in a solution: τ j-D := τ j-D + number of 1-1 contacts in the solution / const;

29. Protein folding Best reported results for different size instances GA: genetic algorithm EMC: evolutionary algorithm + Monte Carlo methods MSOE: Monte Carlo including overlapping conformations PERM: iterated heuristic growing method 47 48 47 100 47 50 50 100 51 53 52 85 42 38 42 39 37 64 36 36 35 34 60 21 21 21 21 50 23 23 23 23 48 14 14 14 14 36 8 8 8 8 25 9 9 9 9 24 9 9 9 9 20 ACO PERM MSOE EMC GA length

30. General comments - where is my manuscript …

31. General comments ACOs : nice, powerful, and robust metaheuristic for NP hard, possibly non -static optimization problems, the solutions of which decompose into single components Applications for ( * = state of the art results for some settings) : quadratic assignment problems * vehicle routing * sequential ordering * shortest common supersequence * scheduling * graph coloring and partitioning telecommunication networks and routing * ... more info on ACOs : Swarm Intelligence, From Natural to Artificial Systems, E.Bonabeau, M.Dorigo, G.Theraulaz, Santa Fe, 1999 http://iridia.ulb.ac.be/~mdorigo/ACO/ Duft der Daten, Der Spiegel , November 13, 2000 Swarm smarts, Scientific American , March 2000

32. General comments Are ACO’s better than other metaheuristics for general optimization problems? No free lunch theorem (Macready/Wolpert) I n the mean, no optimization algorithm is to be preferred! Precise: Assume A and B are finite, B is totally ordered, F is a set of functions from A to B which is closed under permutation, H is a (randomized) search heuristic. Then the expected time to reach the first optimum is independent of H. ... so it might take a while until the ants find my manuscript, but they’ll find it.

33. Rettet die Bildung! Jawoll! Gegen Stellenk ürzungen im Hochschulbereich!

35. ACO-metaheuristic ACO-metaheuristic applicable to general optimization problems as stated above robust and tolerant to changes, e.g. in non-static problems yields state of the art solvers for some problems with modifications daemon actions : improve the found solutions using local search (e.g. k-opt for TSP) elitism : update pheromone only for the (local or global) best ants ...

36. Protein folding – state of the art ACO optimize_solution (i); perform a fixed number of feasible and improving search moves randomly chosen from the following possibilities substitution of a single motif : substitute one motif i-D by a different one i-D’ substitution of a sequence of motifs : substitute all motifs within randomly chosen positions by different motifs long-range moves : substitute one local motif and refold the two ends to feasible settings, whereby the respective original motifs are preserved if possible LRS S RLS LRS L RLS L RSS RLS L SRL RLS LRS S RLS LRS L RLS SL S L RL R