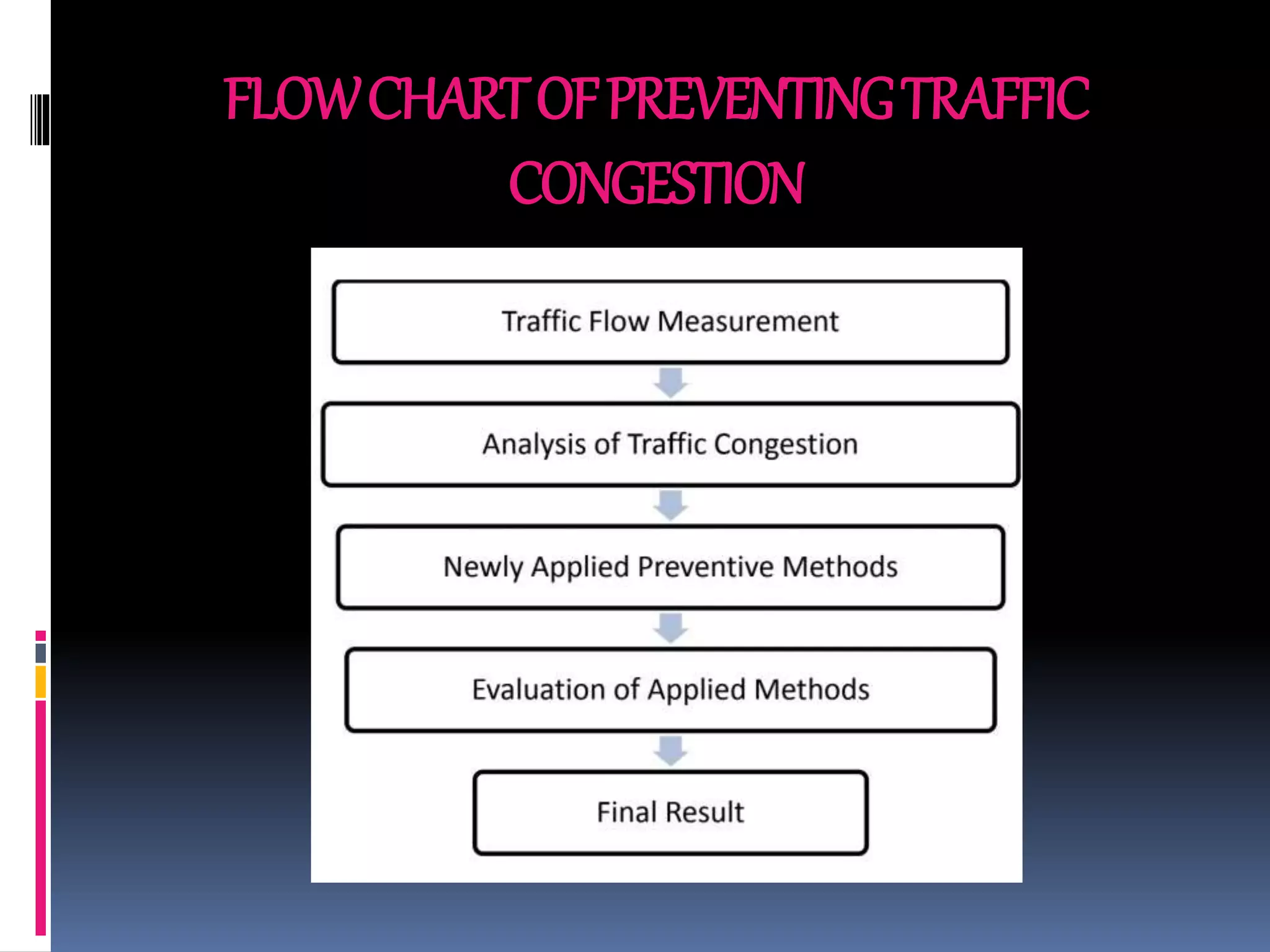
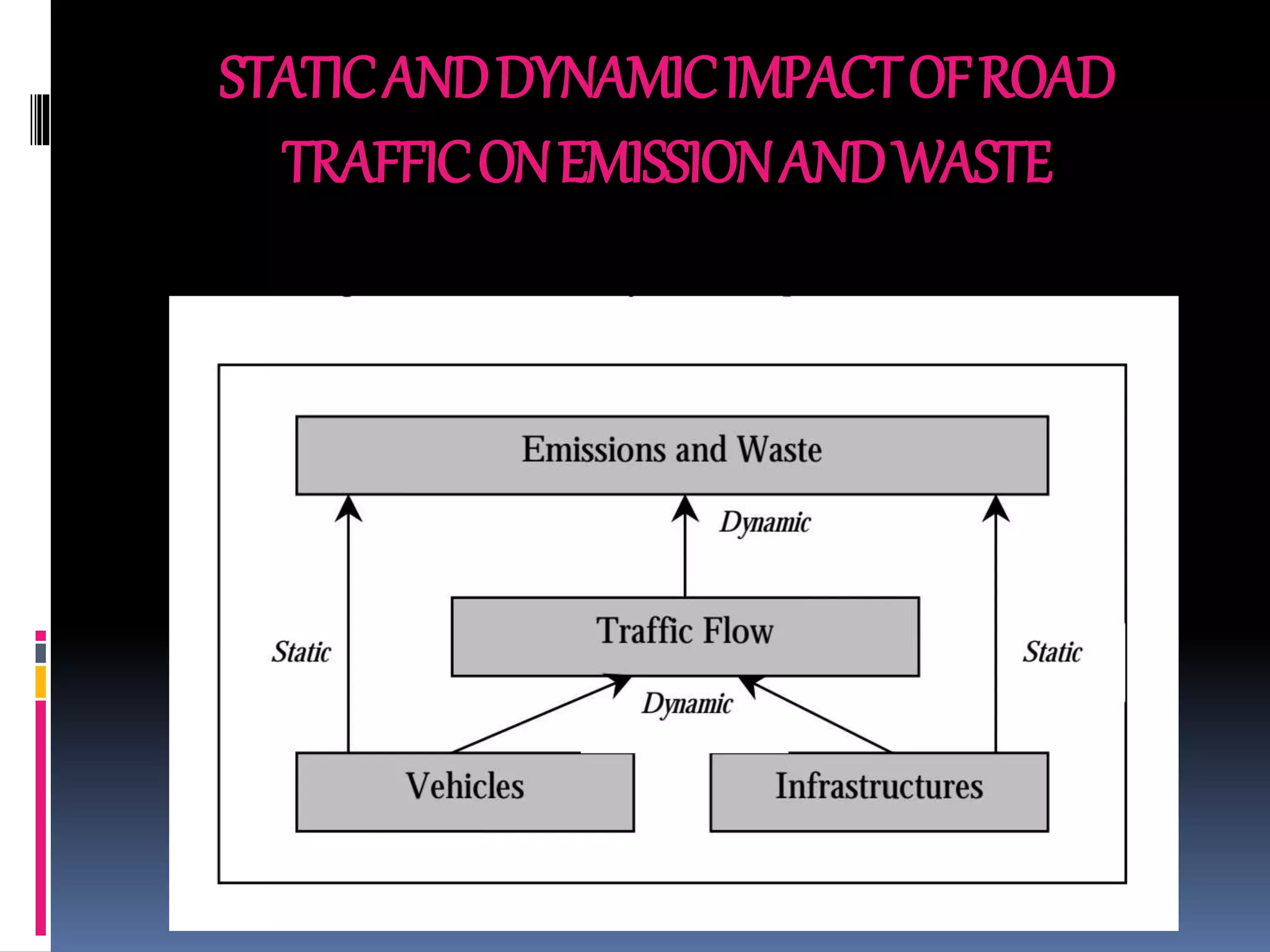
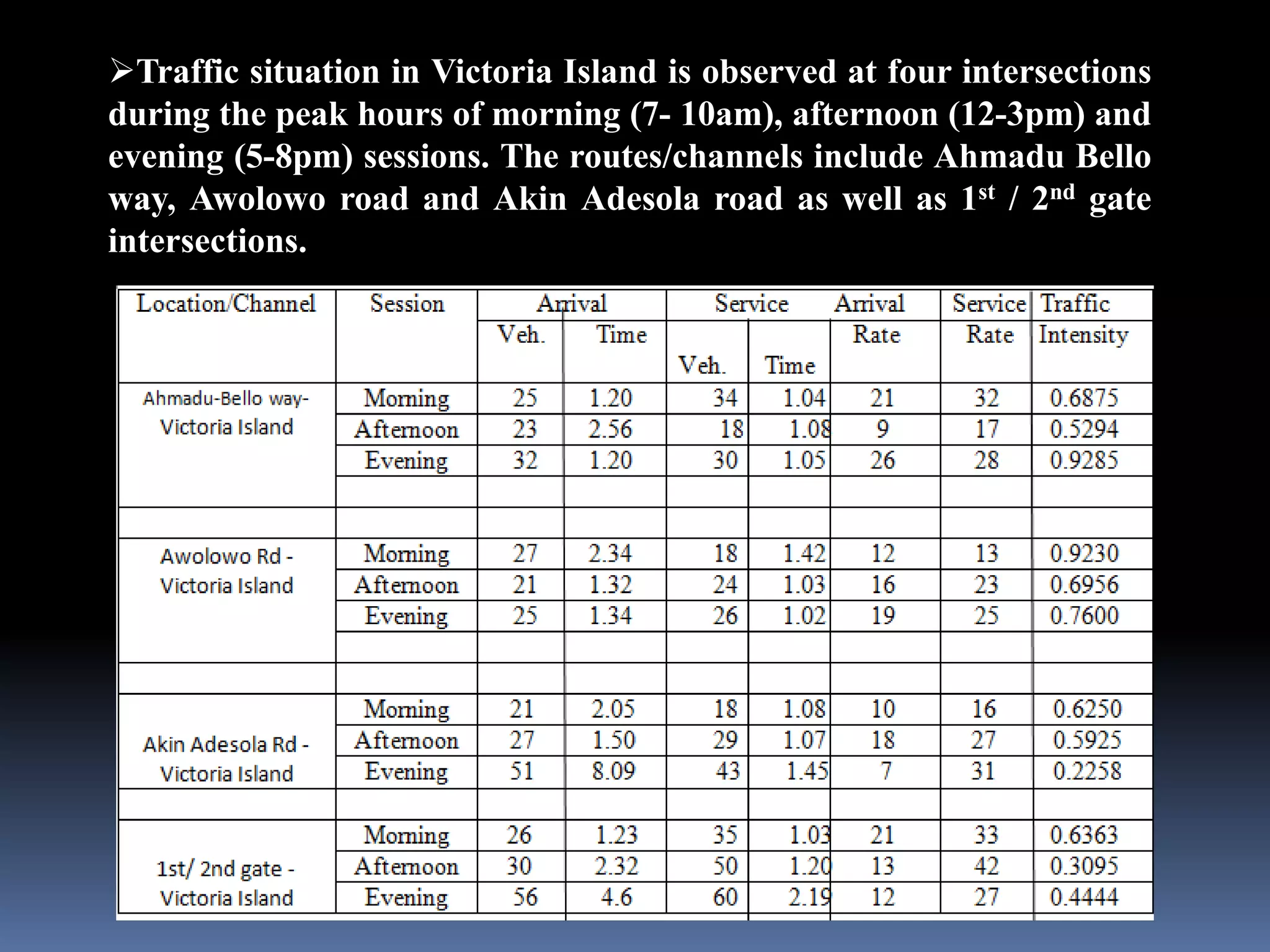
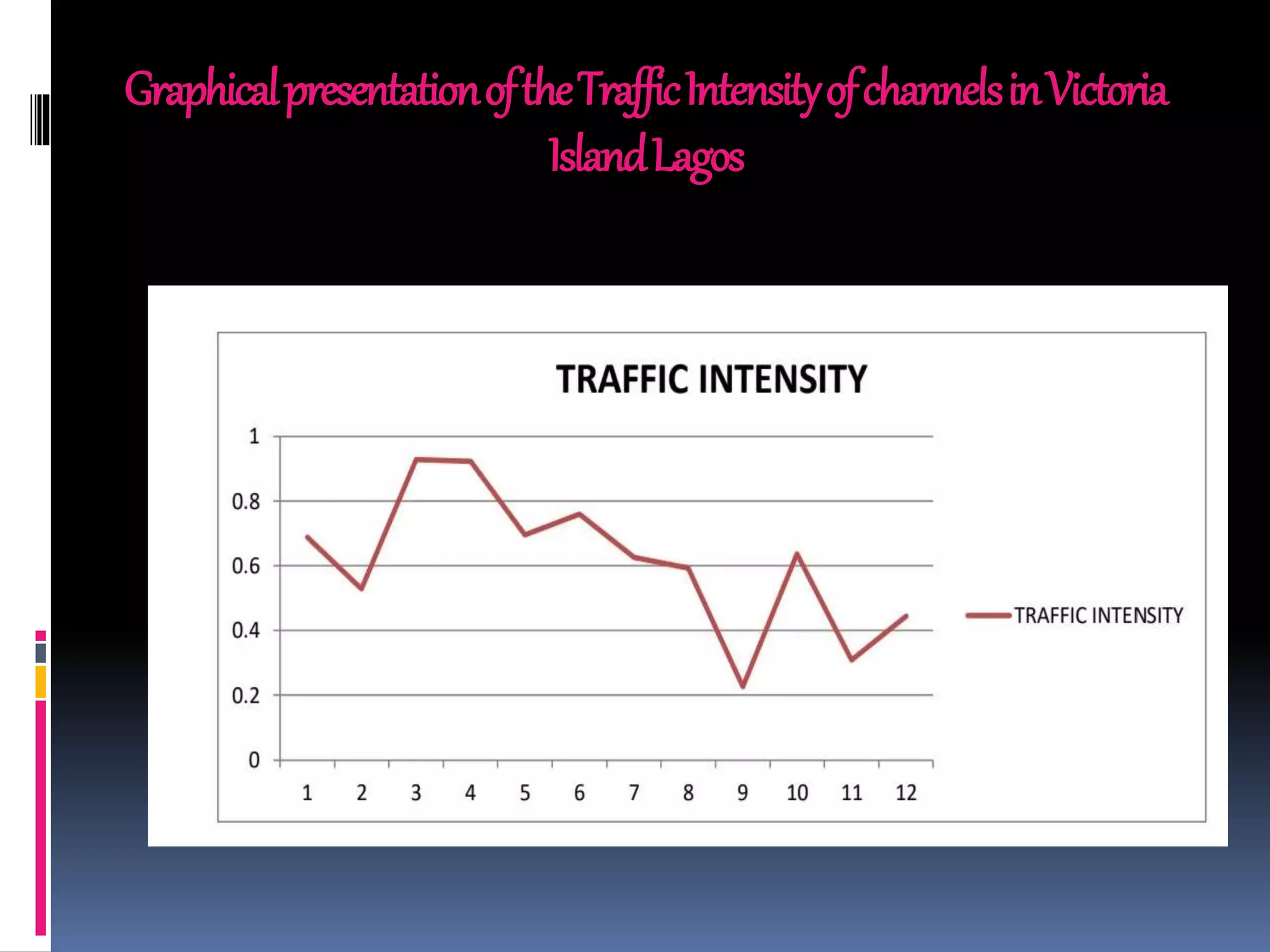
This document discusses the application of queuing theory to traffic management. It presents results from a study of traffic intensity at four intersections in Victoria Island, Lagos during morning, afternoon and evening peak periods. Queuing models were used to determine arrival and service rates, from which traffic intensity was calculated. Morning and evening sessions saw the highest intensities, especially on two roads. The analysis confirms queuing theory can help minimize congestion by optimizing traffic light times during peak periods. Proper road design considering separate lanes, flyovers and parking restrictions can also help ensure smooth traffic flow.

1. A STUDY ON QUEUING THEORY AND ITS
REAL LIFE APPLICATIONS
BY
G.NITHYA .,M.SC.,M.PHIL.,(PH.D)
HEAD AND ASSOCIATE PROFESSOR
DEPARTMENT OF MATHEMATICS
SRI ADI CHUNCHANAGIRIWOMEN’S COLLEGE
CUMBUM.
Mail id : nithyarajkumar15@gmail.com

2. ABSTRACT
 In this paper we took a brief look into the basic
concepts, characteristics, models and
formulation of queuing theory along with
examples of the models and applications of
their use. Applications of queuing theory are
found in fields such as traffic control, hospital
management and timeshared computer system
design. We also discuss about Traffic
congestion and how Queuing Theory is applied
in the management of Traffic intensity.

3. QUEUINGTHEORY
 The mathematical study of waiting lines or
queues is known as queuing theory. The study
of queues deals with measuring the
phenomenon of waiting lines using
representative measures of performances such
as average queue length, average waiting time
in queue and average facility utilization.

4. CALLINGPOPULATION
The population of potential customers those require
service from system is called calling population. It may be
finite or infinite. System having large calling population is
usually considered as infinite.
Ex: Queuing system of finite population
Cars parked in a garage
waiting to repair
Ex: Queuing system of infinite population
Boxes waiting to be packed in a
factory

5. Arrival Process:
 The arrival process for infinite-population models is usually
characterized in terms of inter-arrival times of successive
customers. Arrivals may occur at scheduled times or at random times.
 When at random times, the inter arrival times are usually
characterized by a probability distribution and most important model
for random arrival is the Poisson process. In schedule arrival inter-
arrival time of customers are constant.
Service Process:
 Service process can be measured by the number of customers served
per some unit of time or the time taken to complete the service.
 Once entities have entered to the system they must be served. The
service can be provided in single or batch.
 If it is batch, as in the case of arrival the batch size can be fixed or
random.
 Service time may be of constant duration or of random duration.

6. Queuing Discipline:
Queue discipline refers to the rule that a server uses to choose the next
customer from the queue when the server completes the service of the
current customer.
Common queue disciplines include First-In-First-Out (FIFO), Last-
In-First-Out (LIFO), Service In Random Order (SIRO), Shortest
Processing Time First (SPT) and service according to Priority (PR).
Queuing Behavior:
Queue behavior refers to the actions of customers while in a queue
waiting for service to begin. Different queue behaviors are
Balking
Reneging
Jockeying

7. Number of Servers:
Servers represent the entity that provides service to the customer. A
system may consist of single server or multiple servers. A system with
multiple servers is able to provide parallel services to the customers.
So a queuing system can be classified according to the number of servers as
Single server queuing system
Multi server queuing system

8. ApplicationsofQueuingTheoryinvariousfields
 Bank ATMs:
In ATM, bank customers arrive randomly and the service time i.e., the
time customer takes to do transaction in ATM, is also random. We use
queuing model to derive the arrival rate, service rate, utilization rate,
waiting time in the queue and the average number of customers in the
queue. Queuing can help bank ATM to increase its quality of service, by
anticipating, if there are many customers in the queue.
Hospitals:
Queuing models are used for estimating the waiting time of a patient,
utilization of service, models system design, and models for evaluating
appointment systems. A queuing system helps minimizing the waiting
time of patients and maximizing the utilization of the servers i.e.,
doctors, nurses, hospital beds etc. Queuing is not new but recently
hospitals has begun to use it effectively.

9. Little’sLaw
Little’s Law says that, under steady
state conditions, the average number of
items in a queuing system equals the
average rate at which items arrive
multiplied by the average time that an
item spends in the system.
L=𝜆W

10. UsefulnessofLittle’sLawinPractice
E-mail:
Managing our e-mail is a common and time-consuming daily activity. For
many it is hard to keep up with the volume of messages, let alone provide
timely responses. A student Sue might receive 50 messages each day to
which she must generate a response. Can we easily assess how well this
student handles her e-mail duties?
Indeed we can apply Little’s Law to get a quick sense of how promptly
Sue responds to messages. Suppose that she receives about 50 messages
everyday; then this is the arrival rate: 𝜆 = 50 messages per day. Suppose
we can also track how many messages have yet to be answered. For
instance, suppose that Sue removes a message from her inbox once she has
responded to it. Then the remaining messages in her inbox are the
messages that are waiting to be answered. Over the last semester, the size
of the inbox has varied between one and two hundred messages with an
average of 150 messages. Then we can regard this to be the system queue
length: L = 150 messages. From Little’s Law we immediately have an
estimate of how long it takes Sue to answer a message, on average: W = 3
days.

11. TRAFFICCONGESTION
 Congestions are formed due to different reasons like reduced capacity of
road stretch, accidents, overcrowding etc. Traffic congestions are always
frustrating to the road users.
Traffic congestion is a situation on road network which occurs as its use
increases. It is characterized by slower speeds, increased trip times and
queuing of vehicles.
The effect of traffic jam includes commuter’s frustration, vehicle
collision and fuel wastage.
 The traffic congestions results in delays. Delay is a more subtle concept.
 These delays will surely end up in queues. Queues occur whenever
immediate demand exceeds the capacity to provide a service. Here the
need of application of queuing theory arises.

12. FLOWCHARTOFPREVENTINGTRAFFIC
CONGESTION

13. ENVIRONMENTALIMPACTOFROADTRAFFIC
When modeling the environmental impact of road traffic, we can
distinguish between both a static and dynamic impact of infrastructures and
vehicles on emissions and waste.
On the one hand, roads can be considered as a visual intrusion. In addition,
they may cause damage to natural watercourses or threaten the natural
habitat of wildlife.
Vehicles in use produce emissions and noise. Toxic escape in the
atmosphere when fuel tanks are filled, while driving leads to further
emissions (CO2, NO2 and SO2) and dust (concrete, asphalt and rubber
dust).
Traffic flows are a function of both the number of vehicles on the roads and
the vehicle speed, the resulting environmental impact will also be a function
of these parameters.

14. STATICANDDYNAMICIMPACTOFROAD
TRAFFICONEMISSIONANDWASTE

15. MANAGEMENTOFTRAFFICINTENSITY
Queuing theory is used in minimizing vehicular traffic congestion using
four routes/channels in Victoria Island.
The study also adopts the FIFO (first in first out) approach where the
vehicles are made to line up or queue according to their time of arrival as
customers waiting to be served by a signal of functioning traffic light in a
given channel or location to minimize traffic congestion.
The number of vehicles in each service station for every channel is
counted and the time in minutes noted when waiting to be served and after
being served.
These values are used to derive the arrival and service rates of the
vehicles.
The investigation is based on traffic intensity on some areas in Victoria
Island, Lagos.

16. Traffic situation in Victoria Island is observed at four intersections
during the peak hours of morning (7- 10am), afternoon (12-3pm) and
evening (5-8pm) sessions. The routes/channels include Ahmadu Bello
way, Awolowo road and Akin Adesola road as well as 1st / 2nd gate
intersections.

17. GraphicalpresentationoftheTrafficIntensityofchannelsinVictoria
IslandLagos

18. RESULTORANALYSIS
Morning session:
Ahmadu Bello way- Victoria Island:
The arrival and service rates are 21 and 32 respectively and hence the
traffic intensity is 0.6563. This is an indication of a stable traffic situation
but not a very smooth flow of traffic. The mean number of vehicles in the
system (Ls) and queue (Lq) as well as the mean waiting time in the system
(Ws) and queue (Wq) tend to confirm the traffic situation.
Awolowo road– Victoria Island:
The arrival and service rates are 12 and 13 respectively and hence the
traffic intensity is 0.9230 which is almost unity. This is an indication of an
unstable and critical traffic flow. The derived values of Ls, Lq, Ws and Wq
support the traffic situation.

19. Afternoon session:
Ahmadu Bello way – Victoria Island:
The arrival and service rates are 9 and 17 respectively
and hence the traffic intensity is 0.5294. This is an indication
of a stable and smooth flow of traffic. The derived values are
in line with the reported traffic situation.
Awolowo road– Victoria Island:
The arrival and service rates are 16 and 23 respectively
and hence the traffic intensity is 0.6956. This is an indication
of a relatively unstable and unsmooth traffic flow. The
derived values corroborate the reported traffic situation.

20. Evening session:
Ahmadu Bello way–Victoria Island:
The arrival and service rates are 26 and 28 respectively hence the
traffic intensity is 0.9285 which is close to unity. This is an indication of
an unstable and chaotic traffic flow. It is also the worst condition of
traffic when compared to other channels for all sessions. The traffic
situation is buttressed by the derived parameters.
Awolowo road– Victoria Island:
The arrival and service rates are 19 and 25 respectively and hence the
traffic intensity is 0.7600. This is an indication of a relatively stable but
unsmooth traffic flow. The reported traffic situation is validated by the
derived values.

21. CONCLUSION
This study reveals that traffic intensity is highest in the
morning session when commuters are reporting for
work/business and in the evening session at the close of
work/business especially on Awolowo road and Ahmadu
Bello way respectively.
It is therefore necessary to allot more time at intersections
for traffic into such routes in the morning and evening
sessions.
The increase of traffic light time will reduce traffic
intensity which in turn minimizes delays on such
routes/channels at peak periods of morning and evening
sessions.

22. In the design and implementation of road network, designers and
planners should take into consideration some factors that may engender
free flow of traffic. The consideration should include but not limited to
the following factors:
Construction of separate lanes for commercial vehicles with increased
road capacity.
Construction of flyovers for areas prone to traffic congestion.
Construction of service lanes and bye pass to areas with high traffic
intensity.
Installation of parking restriction signs at strategic points along routes
that are prone to traffic congestion. Enforcement of the parking
restriction is necessary to ensure compliance by private and commercial
vehicles.

23. THANK YOU