This document presents a simulation-based multi-objective design optimization methodology aimed at enhancing the reliability of electronic packaging under thermal cycling and bending. Utilizing a parametric finite element model and a multi-quadric response surface method, the study demonstrates how optimization of design parameters can significantly improve solder joint reliability. The proposed approach effectively identifies global optimum solutions for design variables, thus contributing to better product performance in portable electronics.

1. A simulation-based multi-objective design optimization
of electronic packages under thermal cycling and bending
Leon Xu a,*, Tommi Reinikainen a
, Wei Ren a
, Bo Ping Wang b
,
Zhenxue Han b
, Dereje Agonafer b
a
NOKIA Inc., 6000 Connection Drive, MS 3-4-1400, Irving, TX 75039, USA
b
Mechanical and Aerospace Engineering Department, University of Texas at Arlington, P.O. Box 19018, Arlington, TX 76019, USA
Received 8 September 2003; received in revised form 13 April 2004
Available online 8 July 2004
Abstract
In this study, a simulation-based multi-objective design optimization methodology was developed for improving
electronic packaging reliability. It was demonstrated using a generic model of an electronic package on a printed wiring
board. The objective for the optimization was to improve the reliability of solder joints under both thermal cycling and
bending by optimizing a group of design parameters. A parametric finite element model was developed using ANSYS
for both load conditions. To improve the numerical efficiency of the optimization, a multi-quadric response surface
method was implemented to approximate the response of finite element simulations for each loading condition. Sub-
sequently, the multi-objective optimization of solder joint reliability was implemented using a Minmax principle on all
response surfaces and a differential evolution algorithm as optimal search engine, which is capable of finding global
minimum when local minima exist. Our study demonstrated that the reliability of the solder joints is significantly
improved for this given generic model of electronic package. The proposed methodology can be effectively used in
improving the reliability of electronic packages.
Ó 2004 Elsevier Ltd. All rights reserved.
1. Introduction
Because of increasing demands of functionality and
miniaturization in portable consumer electronics such as
mobile phones, the reliability of the electronic packages
becomes a major concern in product design. In use of
these devices, the electronic packages can be subjected to
various mechanical and/or thermal environments. For
examples, these could happen when pressure is applied
on key pad, or accidental abuse such as sitting-on and
dropping, or large data transmission when browsing
web, or sharp temperature changes when using the de-
vices from indoor to outdoor in winter time. Mechani-
cal/thermo-mechanical failures of interconnects between
electronic packages and printed wiring board (PWB) are
among the major failure mechanisms.
Material and structural properties of a portable
electronics are closely associated with the mechanical/
thermo-mechanical failures of electronic packages under
various loading conditions. For example, it is the mis-
match of the coefficient of thermal expansion (CTE) of
substrate of chip scale packages (CSP) and PWB that
causes the fatigue failure of the solder joints under
thermal cycling. Also, the thickness of PWB has signif-
icant effect on solder joint failure under bending.
With the increasing computer power, the large-scale
numerical simulation of the mechanical phenomenon is
becoming a realistic and routine tool in the electronic
packaging reliability studies. Finite element (FE) simu-
lations have been widely used in analyzing the failures of
the electronic packages to explore the directions of de-
sign improvement. Indeed there are numerous studies of
solder joint reliability of the electronic packaging under
*
Corresponding author.
E-mail address: leon.xu@nokia.com (L. Xu).
0026-2714/$ - see front matter Ó 2004 Elsevier Ltd. All rights reserved.
doi:10.1016/j.microrel.2004.04.024
Microelectronics Reliability 44 (2004) 1977–1983
www.elsevier.com/locate/microrel

2. the thermo-mechanical and bending load in the litera-
ture [1–7]. Though an accurate prediction of the thermal
and bending fatigue life using numerical simulations is
not an easy task, one of the biggest advantages of the
numerical simulations over the experimental investiga-
tion is that it is possible to isolate the effect of certain
parameters on the system response and investigate the
effects of each individual design variable or a group of
design variables. Design space exploration with finite
element thermal stress/strain analyses could help engi-
neers to better understand the reliability behavior under
thermal cycling conditions during the product design
stage quickly. However, the real challenge is to clearly
understand how the design parameters individually and
interactively affect the reliability of the products where
there often exist multiple failure mechanisms. A more
systematic methodology has to be implemented for the
product designs with potential complex multi-modal
failures. As one of the new industrial trends, design
optimization methodology has been used more and
more as an effort to find the best path to improve the
reliability of electronic packages [8,9].
Design optimization has been widely used in auto and
aerospace industries. There have been many optimiza-
tion algorithms proposed in the literature [10–12], with
each having its advantages and disadvantages. There are
generally two categories of algorithms. One is the clas-
sical gradient-based methods, such as sequential qua-
dratic programming [10], which are numerically efficient
but limited to finding the local minimum (or maximum).
Another is the stochastic-based methods, such as genetic
algorithm (GA) [11] and differential evolution (DE) [12],
which are capable of finding the global minimum (or
maximum) when local minima (or maxima) exist.
However, the computational costs for these stochastic-
based methods are usually expensive. There is a tradeoff
to be made between optimization capabilities and com-
putational costs, depending on the specific problem.
In general, the behavior of objective functions of a
design optimization problem is usually unknown a prior.
There may exist several local minima (or maxima) in the
objective functions over a specific design space. The
employed optimization algorithm should be robust and
possess the capability to find the global minimum (or
maximum) in the multi-objective function, even with
necessary computational costs. However, computational
cost is a very important issue in design optimization,
particularly for simulation-based design optimization
because FE simulations involved in electronic packages
are usually very complicated and time-consuming, con-
sidering the complexity in structures and the nonlin-
earity in material behavior. Hundreds or even thousands
of objective function evaluations required in optimiza-
tion really present a tremendous difficulty in reality to
perform a simulation-based design optimization. One
remedy is to use response surface methodology (RSM)
which has become a popular tool for multi-disciplinary
optimization [13,14]. The RSM-based design optimiza-
tion methods use mathematical models (i.e., response
surfaces) to approximate the objective functions of
the system in design space. Subsequently the optimum
search is performed on the response surfaces. Because
the response surfaces pave ‘paths’ for the optimum
search, RSM-based design optimization methods are
usually much more efficient numerically than the direct
methods. There have been many different RSMs pro-
posed, which was nicely reviewed in a previous study
[15], including polynomials, adaptive splines, radical
basis functions, and kriging, etc. Recent studies have
indicated that multi-quadric functions [16], a type of
radical basis functions are among the most accurate and
robust for simulating multi-variate response surface
models than many other mathematical models [15,17].
In this study, a simulation-based multi-objective de-
sign optimization method was developed for improving
electronic packaging reliability. In order to improve the
numerical efficiency of optimization, a multi-quadric
RSM was implemented. Furthermore, a DE algorithm is
used as the search engine in the multi-objective function
minimization procedure, which is capable of finding
global minimum when local minima exist. This method
was demonstrated by a generic model of an electronic
package on a PWB. The objective was to improve the
reliability of solder joints for both thermal cycling and
bending. Two response surfaces were created based on
the data points from FE simulations for thermal cycling
and bending, respectively. Subsequently, a global re-
sponse surface (which considers reliability under both
loading conditions) was created based on the individual
response surfaces using a Minmax principle. Finally,
optimum search for both thermal and bending was
performed on the global response surface.
2. Methods
In general, a design optimization problem can be
stated as a mathematical problem as follows:
Minimize OBJiðXÞ ði ¼ 1; nÞ
while gjðXÞ ¼ 0 ðj ¼ 1; mÞ
hkðXÞ 6 0 ðk ¼ 1; LÞ
and XL
6 X 6 XU
where OBJiðXÞ are objective functions; gjðXÞ are
equality constraints; hkðXÞ are in-equality constraints; X
are design variables; n is the number of objective func-
tions; m is the number of equality constraints; L is the
number of in-equality constraints; XL
and XU
are lower
and upper bounds of the design variables, respectively.
1978 L. Xu et al. / Microelectronics Reliability 44 (2004) 1977–1983

3. A generic mechanical model was used as a test vehicle
to develop the simulation-based multi-objective design
optimization method. In this model, a CSP is mounted
on a PWB which is subjected to thermal cycling and
bending. The CSP includes substrate, die, die attach, and
mounding compound, while the PWB was modeled as a
uniform layer. Table 1 and 2 gives geometric dimensions
and material properties of the model. The objective is to
find an optimal design solution such that this CSP–PWB
assembly has the best reliability in solder joints consid-
ering both thermal cycling and bending, where the
maximum inelastic work of the solder joints was used as
a measurement of the solder joints reliability. There are
two individual optimization objectives for the problem:
one is to minimize the inelastic work of solder joint
under thermal cycling, while another is to minimize the
inelastic work of solder joint under bending. The global
optimization objective is to find the best design solution
considering both cases. The design parameters used for
optimization are the geometric and material properties
of the PWB as well as the solder joint height. Table 3
gives the ranges of design parameters. Note that the
emphasis of this research is to demonstrate the design
optimization methodology for the reliability of elec-
tronic packages. Hence the design space defined in Table
3 covers a fairly large range of design parameter varia-
tions to take the full advantages of the methodology. No
constraints were applied in this study.
Three major steps were taken in our method. It in-
cludes: establishing an FE model of the CSP–PWB
assembly, creating individual response surface of
inelastic work of solder joint for each loading condition,
and optimizing the global multi-objective function. The
details are as follows.
2.1. FE model
The finite element model is written using the
ANSYSâ
APDL language, and is fully parametric
regarding all relevant dimensions and material proper-
ties. FE mesh is shown in Fig. 1. Because of the sym-
metry of the model, only a quarter model was created.
All materials are modeled as linear elastic, except for the
solder material that is modeled by the Anand’s visco-
plastic model using the parameters determined by Dar-
veaux et al. [2] in thermal cycling simulations and our
own parameters based on experiments for bending
Table 2
CSP–PWB assembly material properties
Young’s modulus (GPa) Shear modulus (GPa) Poisson’s ratio CTE (ppm)
PWB 28 (11) 9.78 (5.4) 0.11 (0.39) 16.0 (62.0)
Substrate 25.0 (11.0) 9.0 (5.0) 0.11 (0.39) 17.0 (62.0)
Die 131.0 0.3 2.8
Die attach 2.3 0.4 50.0
Molding compound 35.0 0.25 8.0
Solder mask 6.0 0.30 95.0
Cu pad 117.0 0.30 17.7
Solder ball 35.27 0.4 25.0
Note: The number in brackets denotes out-plane value.
Table 1
CSP–PWB assembly dimensions
PWB (mm) 100.0 · 100.0 · 1.0
PWB solder mask (mm) 13.0 · 13.0 · 0.028
PWB pad thickness (mm) 0.028
PWB pad diameter (mm) 0.315
Die (mm) 7.2 · 7.2 · 0.2
Die attach (mm) 7.2 · 7.2 · 0.03
Mold compound (mm) 13 · 13 · 0.5
Substrate (mm) 13 · 13 · 0.2
Substrate mask (mm) 13 · 13 · 0.038
Solder standoff height (mm) 0.2
Solder ball pitch (mm) 0.8
Solder diameter (mm) 0.47
Substrate pad diameter (mm) 0.315
Table 3
Selected design variables
Nominal design Lower bound Upper bound
PWB in-plane Young’s modulus (GPa) 28.0 20.0 35.0
PWB CTE (ppm) 16.0 12.0 18.0
PWB thickness (mm) 1.0 0.5 1.2
Solder joint height (mm) 0.20 0.18 0.22
L. Xu et al. / Microelectronics Reliability 44 (2004) 1977–1983 1979

4. simulations. Under bending load, a triangular cyclic
displacement (0–1.5 mm, 1 Hz) was applied on the
bottom center of the PWB while the four corners of the
PWB are fixed. For thermal simulation, isothermal
temperature cycling ()40 to 125 °C) is applied, with 3.5
min ramps and 12 min dwells at both temperature ex-
tremes. Three full temperature cycles are imposed on the
package assembly to simulate the thermo-mechanical
loading condition. It was noticed that the change of the
plastic work increment per temperature cycle is negligi-
ble after three full cycles. The plastic work increment in
the critical solder joint during the last cycle is used as a
measure of the thermo-mechanical performance of the
package assembly.
It has to be pointed out that a global finite element
model, which has relatively coarse mesh density in solder
joints, is adopted in the FE analyses because of its great
saving in computing time. Of course, the numerical
simulation results obtained with this global finite ele-
ment model may be less accurate if compared to the
models with finer mesh of the solder joints. However,
our study indicates that this global model finds the same
location of the critical solder joint, and provides the
same trend in the changes of the maximum plastic work
(due to the changes of the specific design parameters),
compared to those from the global/local models [6,7]
which have much finer meshes in solder joints and have
been verified previously. Indeed the role of the FE
analysis in the design optimization procedure is to find
the trend of design changes, i.e., to tell if a particular
design is better or worse than others. Therefore, the
accuracy of the results from FEA is not as important as
in the fatigue life predictions of the solder joints, as long
as the design trends are correct. Using the simplified
model, it could enhance the numerical efficiency of
simulation-based design optimization significantly.
2.2. Multi-quadric response surfaces
In multi-quadratic approximation, the response at a
design point x is approximated by the following formula
[9,10]
F ¼
Xn
j¼1
CjUjðxÞ ¼ ½UŠfCg
where UjðxÞ is the multi-quadric function given by
UðxÞ ¼
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
jx À xjj2
þ h
q
The parameter h is known as the smooth parameter. The
unknown Cj coefficients can be computed by requiring
the function F passing through a given set of data
ðXj; FjÞ. In the present work, h is set to 1.0. Ref. [16,17]
give the details on how to build a multi-quadric response
surface.
Two response surfaces were created, where the
dependent variable is the maximum inelastic work of
the solder join under specific loading condition, while
the inputs are the prescribed design parameters. To get
accurate response surfaces, a method which employs
multi-quadric RSM and DE optimal search iteratively
was used. For each loading condition, initially, a re-
sponse surface was created based on the simulation data
from FE analyses based on a design of experiment
(DOE) matrix using latin hypercube sampling scheme.
Subsequently, a DE algorithm was applied to find the
minimum of the specific response surface. If this opti-
mum did not match with the result from FE simulation,
the FE simulation result was added to the previous
database and a new response surface was created. This
process was repeated iteratively until the optimum of
each response surface matches the result from the cor-
responding FE simulation.
2.3. Optimization of multi-objective function
With the established response surfaces for individual
loading conditions, an argumented objective function
for the multi-objective optimization was formulated
using Minmax principle [18] as follows:
OBJ ¼ MinimumfMaximum½wifiðXÞŠg
where fiðXÞ is the individual response surface for specific
loading conditions, while wi is the weight coefficient
depending on the importance of the individual functions
in the global objective. The design space X was kept the
same as the individual response surfaces. For a given
multi-objective optimization problem, in general, there
are multiple solutions, depending on the weight of
individual optimization objectives. In this study, wi was
selected based on the fatigue life prediction of solder
joints under thermal cycling and bending as well as the
general product requirement (0.1 for thermal cycling and
0.9 for bending). Finally, a DE searching algorithm is
applied again for the optimal design of the model.
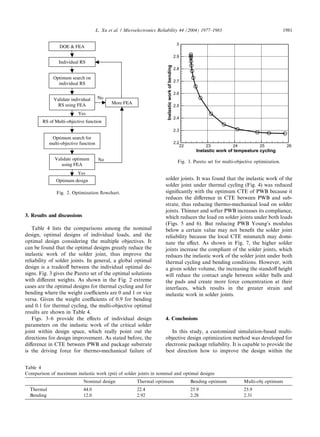
In summary, Fig. 2 gives the flowchart of this simu-
lation-based multi-objective design optimization method.
For this model, the individual runtime for each FE
simulation is around 3.5 h. Totally 48 data points were
generated for establishing the individual response sur-
faces of the maximum inelastic work of solder joints.
Fig. 1. Finite element meshes of CSP–PWB assembly.
1980 L. Xu et al. / Microelectronics Reliability 44 (2004) 1977–1983

5. 3. Results and discussions
Table 4 lists the comparisons among the nominal
design, optimal designs of individual loads, and the
optimal design considering the multiple objectives. It
can be found that the optimal designs greatly reduce the
inelastic work of the solder joint, thus improve the
reliability of solder joints. In general, a global optimal
design is a tradeoff between the individual optimal de-
signs. Fig. 3 gives the Pareto set of the optimal solutions
with different weights. As shown in the Fig. 2 extreme
cases are the optimal designs for thermal cycling and for
bending where the weight coefficients are 0 and 1 or vice
versa. Given the weight coefficients of 0.9 for bending
and 0.1 for thermal cycling, the multi-objective optimal
results are shown in Table 4.
Figs. 3–6 provide the effects of individual design
parameters on the inelastic work of the critical solder
joint within design space, which really point out the
directions for design improvement. As stated before, the
difference in CTE between PWB and package substrate
is the driving force for thermo-mechanical failure of
solder joints. It was found that the inelastic work of the
solder joint under thermal cycling (Fig. 4) was reduced
significantly with the optimum CTE of PWB because it
reduces the difference in CTE between PWB and sub-
strate, thus reducing thermo-mechanical load on solder
joints. Thinner and softer PWB increases its compliance,
which reduces the load on solder joints under both loads
(Figs. 5 and 6). But reducing PWB Young’s modulus
below a certain value may not benefit the solder joint
reliability because the local CTE mismatch may domi-
nate the effect. As shown in Fig. 7, the higher solder
joints increase the compliant of the solder joints, which
reduces the inelastic work of the solder joint under both
thermal cycling and bending conditions. However, with
a given solder volume, the increasing the standoff height
will reduce the contact angle between solder balls and
the pads and create more force concentration at their
interfaces, which results in the greater strain and
inelastic work in solder joints.
4. Conclusions
In this study, a customized simulation-based multi-
objective design optimization method was developed for
electronic package reliability. It is capable to provide the
best direction how to improve the design within the
DOE & FEA
Individual RS
Optimum search on
individual RS
Validate individual
RS using FEA More FEA
RS of Multi-objective function
Optimum search for
multi-objective function
Validate optimum
using FEA
No
Yes
No
Yes
Optimum design
Fig. 2. Optimization flowchart.
Table 4
Comparison of maximum inelastic work (psi) of solder joints in nominal and optimal designs
Nominal design Thermal optimum Bending optimum Multi-obj optimum
Thermal 44.0 22.4 25.9 23.9
Bending 12.0 2.92 2.28 2.31
Inelastic work of tempeature cycling
Inelasticworkofbending
22 23 24 25 26
2.2
2.3
2.4
2.5
2.6
2.7
2.8
2.9
3
Fig. 3. Pareto set for multi-objective optimization.
L. Xu et al. / Microelectronics Reliability 44 (2004) 1977–1983 1981

6. design space. Use of RSM can greatly reduce the com-
putational cost, which is very significant when the
associated FE model is complex and highly nonlinear.
Furthermore, DE optimation algorithm provides a
searching engine which is efficient and capable of finding
the global minimum when local minima exist. The whole
process is proven robust and effective numerically.
As all simulation-based analyses, cautions should be
paid when interpreting the results from optimization.
Experimental tests have to be performed to verify the
optimal design. However, this simulation-based multi-
objective design optimization method provides a tool for
the directions of reliability improvement in product de-
sign phase. This could potentially eliminate severe reli-
ability problems in design phase and significantly reduce
the product cycles and cost.
References
[1] Pao YH. A fracture mechanics approach to thermal fatigue
life prediction of solder joints. IEEE CHMT 1992;
15(4):559–70.
[2] Darveaux R et al. Reliability of plastic ball grid array
assembly. In: Lau J, editor. Ball grid array technology.
New York: McGraw-Hill, Inc.; 1995. p. 379–442.
[3] Syed AR. Creep crack growth prediction of solder joints
during temperature cycling––an engineering approach. In:
Transactions of the ASME, vol. 117. 1995. p. 116–22.
[4] Syed AR. A review of finite element methods for solder
joint analysis, 1996. In: Proceedings of Experimental/
Numerical Mechanics in Electronic Packaging, SEM,
vol. 1. p. 117–25.
ThermalInelasticWork(psi)
BendingInelasticWork(psi)
Solder Height (mm)
0.15 0.16 0.17 0.18 0.19 0.2 0.21 0.22
0
5
10
15
20
25
30
35
40
45
50
55
60
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Thermal
Bending
Fig. 7. Inelastic work of solder joint vs solder height.
PWB CTE (ppm)
ThermalInelasticWork(psi)
12 13 14 15 16 17 18
0
5
10
15
20
25
30
35
40
45
50
Thermal
Fig. 4. Inelastic work of solder joint vs PWB CTE.
ThermalInelasticWork(psi)
PWB Young's Modulus (GPa)
BendingInelasticWork(psi)
20 25 30 35
0
5
10
15
20
25
30
35
40
45
50
55
60
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Thermal
Bending
Fig. 5. Inelastic work of solder joint vs PWB in-plane Young’s
modulus.
ThermalInelasticWork(psi)
BendingInelasticWork(psi)
PWB Thickness (mm)
0.5 0.6 0.7 0.8 0.9 1 1.1 1.2
0
5
10
15
20
25
30
35
40
45
50
55
60
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Thermal
Bending
Fig. 6. Inelastic work of solder joint vs PWB thickness.
1982 L. Xu et al. / Microelectronics Reliability 44 (2004) 1977–1983

7. [5] Syed AR. Factors affecting creep-fatigue interaction in
eutectic Sn/Pb solder joints. In: Advances in Electronic
Packaging 1997, Interpack97. p. 1535–42.
[6] Wang J et al. Effect of cleaning & non-clearing situations
on the reliability of flip-chip packages. IEEE Trans
Components Pack Technol 1999;22(2):221–8.
[7] Tommi R et al. An optimized shear test sample for
assessing solder deformation properties. In: Proceedings of
the 2nd International Conference on ESIME, Paris,
France, April 2001. p. 133–6.
[8] Wang BP et al. Design optimization for PWB level
electronic packaging reliability under thermal cycling load.
In: 2002 ASME International Mechanical Engineering
Congress & Exposition, New Orleans, LA, November
2002, IMECE2002-39655.
[9] Obinelo IF. Design and optimization of A 1U motorized
impeller tray for Gtelecom applications. In: 2002 ASME
International Mechanical Engineering Congress & Expo-
sition, New Orleans, LA, November 2002, IMECE2002-
39654.
[10] Luenberger DG. Linear and nonlinear programming. New
York: Addison Wesley; 1984. p. 167–292.
[11] Goldberg DE. Genetic algorithm in search, optimization
and machine learning. Reading: Addison Wesley Long-
man; 1989.
[12] Storn R et al. Differential evolution––a simple and efficient
adaptive scheme for global optimization over continuous
spaces. Technical Report TR-95-ICSI.
[13] Dennis BH et al. Multi-objective optimization of turbo-
machinery cascade for minimum loss, maximum loading,
and maximum gap-to-chord ratio. Int J Turbo Jet Engines
2001;18:201–10.
[14] McDonald DB et al. Response surface model development
for global and local optimization using radial basis
functions. In: AIAA 2000-4776, 8th AIAA/USAF/NASA/
ISSMO Symposium on Multidisciplinary Analysis and
Optimization, Long Beach, CA, September 2000.
[15] Jin R et al. Comparative studies of metamodeling tech-
niques under multiple modeling criteria. Struct Multidis-
ciplinary Optim 2001;23:1–13.
[16] Hardy RL. Multiquadric equations of topography and
other irregular surfaces. J Geophys Res 1971;76:1905–15.
[17] Wang BP. Parameter optimization in multiquadric re-
sponse surface approximations. In: 6th US National
Congress on Computational Mechanics, Symposium on
Design Optimization Applications in Industry, Dearborn,
MI, August 2001.
[18] Castillo E et al. Building and solving mathematical
programming models in engineering and science. New
York: Wiley-Interscience; 2002. p. 395–401.
L. Xu et al. / Microelectronics Reliability 44 (2004) 1977–1983 1983