This document describes a dataflow implementation of Curran's approximation algorithm for pricing Asian options. The implementation computes the value at risk of a portfolio containing Asian options. It supports an arbitrary number of averaging points and achieves high precision using fixed-point arithmetic. Experimental results show that a single Maxeler dataflow engine can price portfolios over 10 times faster than a 48-core CPU. Further optimization including multi-DFE processing and porting to newer FPGA hardware could improve energy efficiency and performance.

1. Politecnico di Milano
Dipartimento di Elettronica, Informazione e Bioingegneria (DEIB)
Anna Maria Nestorov, Enrico Reggiani and Marco D. Santambrogio
{annamaria.nestorov, enrico2.reggiani}@mail.polimi.it
marco.santambrogio@polimi.it
A SCALABLE DATAFLOW IMPLEMENTATION OF
CURRAN’S APPPROXIMATION ALGORITHM
7th June 2017 @ Xilinx

2. 2
Contributions
Thanks to the Maxeler Tools productivity features, we aimed to create an
efficient parametric design which:
1. Computes Value at Risk (VaR) of a portfolio of Asian Options based on
Curran’s approximation method
2. Supports arbitrary number of averaging points

3. 3
• Black-Scholes model: option payoff variable no closed-form representation for
its probability distribution
• Curran's Approximation: expected option payoff conditional on the
geometric mean of the prices at averaging points
• Curran’s algorithm characterised by:
1. High degree of precision
2. Computational intensive
• High number of invocations to the Normal Cumulative Distribution Function
(NCDF), exponentials and logarithms
• Highly parallel computation, completely independent variables are calculated
• Evaluation of one portfolio takes from one to many hours
Curran’s Approximation for Asian Option Pricing

4. 4
• A server-class HPC system comprising:
1. 8 MAX4 MAIA DFEs with an Altera StraXx V FPGA and 96 GB of DRAM each
2. a dual socket Intel Xeon CPU X5650 CPU subsystem with 24 hardware cores per
socket running at 2.67GHz and using 768GB of RAM
1U Maxeler MAX4 MPC-X Architecture

5. 5
• DFE input: N x N x #optionFields
• Initialisation K1, intermediate K3 and finalisation K5 kernels do not
require multi-cycling
• Summation kernels K2 and K4 unroll k summand computations
• DFE output: N S
Data Flow Architecture Single DFE
O S
Infiniband link
Infiniband link

6. 6
• DFE input: N x (N / #DFEs) x #optionFields
• Initialisation K1, intermediate K3 and finalisation K5 kernels do not
require multi-cycling
• Summation kernels K2 and K4 unroll k summand computations
• DFE output: N / #DFEsS
Data Flow Architecture Multi-DFEs
O S
DFEs
Infiniband link
Infiniband link

7. 7
• Two test data sets: DataSet30 and DataSet780
• Precision analysis performed exploiting fixed-point
and floating-point data types, one per build, for the
entire design
• DFE resource usage analysis for the same data types
• Dynamic ranges analysis
Experiments

8. 8
• Domain specific accuracy constraint: precision < 10
Fix32(11,21) Fix48(16,32) Fix54(16,38) Fix64(11,53)
Float32 (8,24) Float48(11,37) Float52(11,41) Float64(11,53)
Precision Analysis Results
-9

9. 9
• 54 and 64 bits fixed-point data representation leads to less resources
than in case of a floating point (through 48, 54 and 64 bits)
DFE Resource Analysis Results

10. 10
• Assuming worst case (linear) scalability resource utilisation with
parameter k
• With Fix54(16,38) maximum value of the unrolling factor k=3
• Dynamic range analysis aiming to increase the unrolling factor
Dynamic Ranges Analysis Results

11. 11
• Assuming worst case (linear) scalability resource utilisation with
parameter k
• With Fix54(16,38) maximum value of the unrolling factor k=3
• Dynamic range analysis aiming to increase the unrolling factor
k=3
Dynamic Ranges Analysis Results

12. 12
• Assuming worst case (linear) scalability resource utilisation with
parameter k
• With Fix54(16,38) maximum value of the unrolling factor k=3
• Dynamic range analysis aiming to increase the unrolling factor
K1
K2 K2 K2 K2
K3
K4 K4 K4 K4
K5
…
…
k=3
Dynamic Ranges Analysis Results

13. 13
• Assuming worst case (linear) scalability resource utilisation with
parameter k
• With Fix54(16,38) maximum value of the unrolling factor k=3
• Dynamic range analysis aiming to increase the unrolling factor
K1
K2 K2 K2 K2
K3
K4 K4 K4 K4
K5
…
…
Float(11,32)
Float(11,32)
Float(11,32)
k=3
Dynamic Ranges Analysis Results

14. 14
• Assuming worst case (linear) scalability resource utilisation with
parameter k
• With Fix54(16,38) maximum value of the unrolling factor k=3
• Dynamic range analysis aiming to increase the unrolling factor
K1
K2 K2 K2 K2
K3
K4 K4 K4 K4
K5
…
…
Float(11,32)
Float(11,32)
Float(11,32)
Fix48(14,34), Fix48(8,40), Fix64(20,40),
Fix54(21,33) and Fix32(32,0)
Fix48(14,34), Fix48(8,40), Fix64(20,40),
Fix54(21,33) and Fix32(32,0)
k=3
Dynamic Ranges Analysis Results

15. 15
• Assuming worst case (linear) scalability resource utilisation with
parameter k
• With Fix54(16,38) maximum value of the unrolling factor k=3
• Dynamic range analysis aiming to increase the unrolling factor
K1
K2 K2 K2 K2
K3
K4 K4 K4 K4
K5
…
…
Float(11,32)
Float(11,32)
Float(11,32)
Fix48(14,34), Fix48(8,40), Fix64(20,40),
Fix54(21,33) and Fix32(32,0)
Fix48(14,34), Fix48(8,40), Fix64(20,40),
Fix54(21,33) and Fix32(32,0)
k=3
k=15
Dynamic Ranges Analysis Results

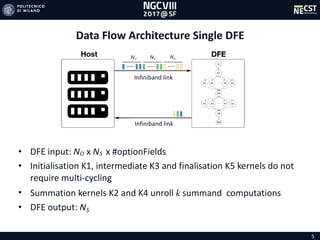
16. 16
Speedups and Energy Efficiencies
s CPU 48 Cores Single DFE
DataSet30
DataSet780
Tabella 1-1
DataSet30 DataSet780
PU 1 Core 21 400
PU 24 Cores 7 36
PU 48 Cores 8 27
ingle DFE 5 6
s CPU 48 Cores Single DFE
DataSet30
DataSet780
Tabella 1-1-1
DataSet30 DataSet780
PU 1 Core 11 30
PU 24 Cores 7 36
PU 48 Cores 8 27
ingle DFE 11 12
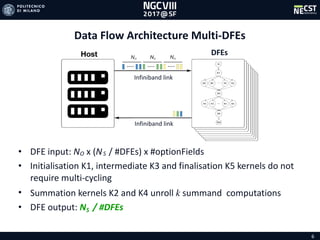
RunTime[s]
1
100
10000
CPU 1 Core CPU 24 Cores CPU 48 Cores Single DFE 8 DFEs
2,181
11,99
238,564240,017
3789,277
1,461,25
10,3310,49
158,81
DataSet30
DataSet780
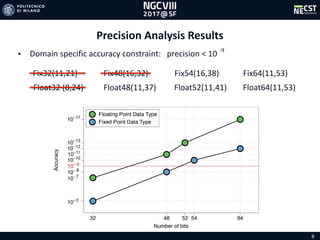
SocketEnergy[Wh]
1
10
100
CPU 1 Core CPU 24 Cores CPU 48 Cores Single DFE 8 DFEs
8
6
27
36
400
55
87
21
DataSet30
DataSet780

17. 17
• An example of large class of HPC application with numerical solvers used
as case study in EXTRA European Project
• Improvements in runtime and energy utilisation offer a compelling
advantage to financial institutions that want to reduce both option pricing
time and energy usage
• DFE:
1. Multi-DFE energy efficiency in progress
2. Porting to the new Maxeler MAX5 based on Xilinx Virtex UltraScale+
• CPU:
1. More improvements to be done
Conclusions and Future Works

18. 18
THANKS FOR THE ATTENTION!
{annamaria.nestorov, enrico2.reggiani}@mail.polimi.it
marco.santambrogio@polimi.it
Acknowledgements to Hristina Palikareva, Pavel Burovskiy and Tobias Becker from Maxeler Technologies London