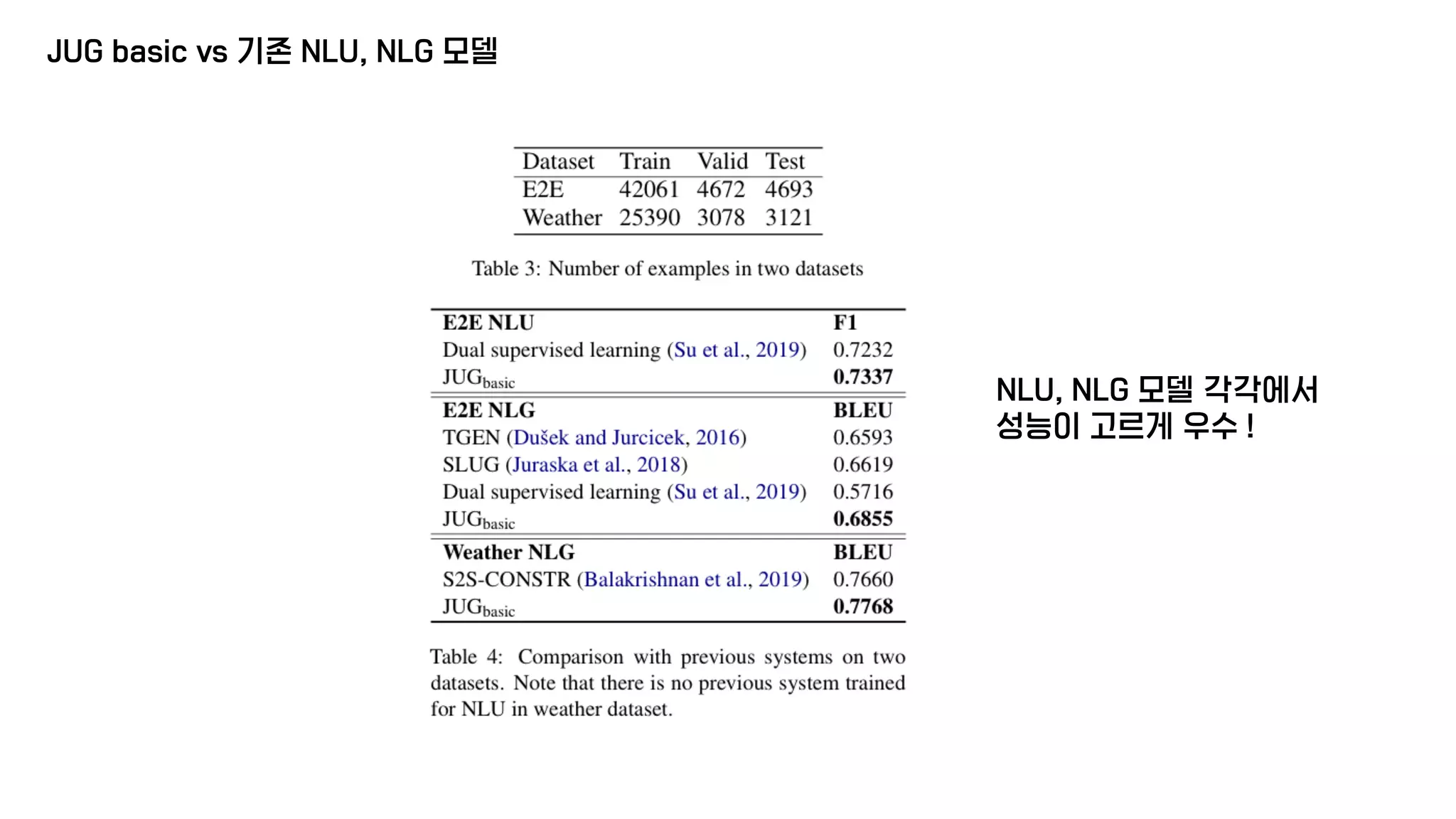
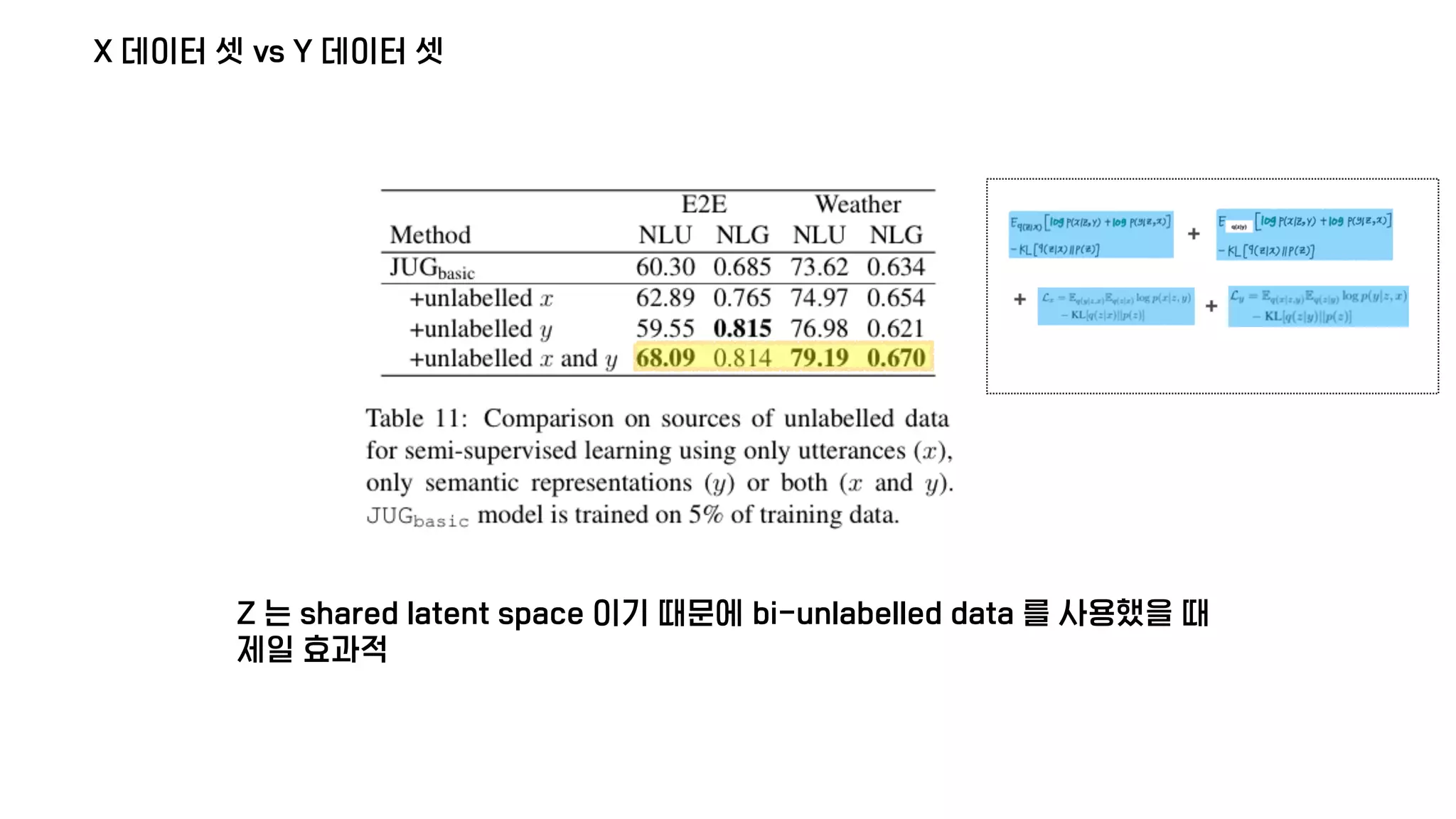
The document presents a generative model for joint natural language understanding (NLU) and natural language generation (NLG), aimed at improving communication between humans and computers. It outlines the model's structure, optimization methods, experimental results, and related research, highlighting the use of latent spaces for efficient information exchange across tasks. The findings indicate that the proposed 'jug model' outperforms existing NLU and NLG models, especially when labeled data is limited.

1. A Generative Model for Joint Natural
Language Understanding and Generation
자연어처리 팀 : 김은희, 백지윤, 주정헌

2. 목차
•연구 목적,모델 구성
•모델 최적화 방법
•실험 및 결과 분석
•연관된 연구

3. 연구 목적 🏹

4. •인간의 언어 소통 : 인간과 인간의 소통
👩
“야 티비 꺼줘”
👧
“나한테 이래라
저래라 하지마”

5. •자연어처리 : 인간과 컴퓨터의 소통
👩
“지니야 티비 꺼줘” “티비를 끕니다”
상식 추론
“티비가 무엇이지?”
목적 기반 대화
“어떠한 명령을
시키는 거지?”
의미론적 구문 분석
“무슨 말을 하는거지?”
🖥
NLU ; 컴퓨터가 자연어를
이해하는 것
NLG ; 컴퓨터가 자연어를
생산하는 것
NLP ; 인간과 컴퓨터가 소통할 수 있도록 하는 일

6. NLU ; 컴퓨터가 자연어를
이해하는 것
x ; 자연어 잠재공간 z Y ; 컴퓨터가 이해한 방식
NLG ; 컴퓨터가 자연어를
생산하는 것
Y ; 컴퓨터가 이해한 방식 잠재공간 z x ; 자연어
잠재공간 z
x ; 자연어 Y ; 컴퓨터가 이해한 방식
1. 잠재공간을 잘 활용하여서 NLU 와 NLG의 성능을 동시에 향상시킬 수는 없을까 ?

7. x ; 자연어
Y ; 컴퓨터가 이해한 방식
2. (x,y) 주석 처리 =
막대한 시간과 비용
잠재공간을 잘 활용하여서
두 과제 사이의 정보 교환
이 원할하게 만들 수 있지
않을까?
= x (y) 데이터만을 가지고 y (x)
데이터를 만들어낼 수 있지 않을까 ?

8. 모델 구성 🤖
step by step

9. 1. NLG
Y
Average-Pooling
Bi-lstm
그런데 똑같은 인풋 Y 를 넣어도 z 는 그때그때 달라진다 ! 😨

10. 1. NLG
Y
그렇다면 z 의 모수를 통해서 z를 추정해주자 !
z는 몇 차원으로 할까 ? = latent_dim
Average-Pooling
Bi-lstm
Dense Dense
μ σ
z_mean=layers.Dense(latent_dim)(y)
z_log_var=layers.Dense(latent_dim)(y)
vae 코드
vae 에서 인코더는 z의 최적화된 모수를 output 으로 산출하도록 학습 !

11. Z 의 차원과 모수에 대한 직관적인 이해
Vary Z1 :
Degree of smile
Vary Z2 :
Head pose
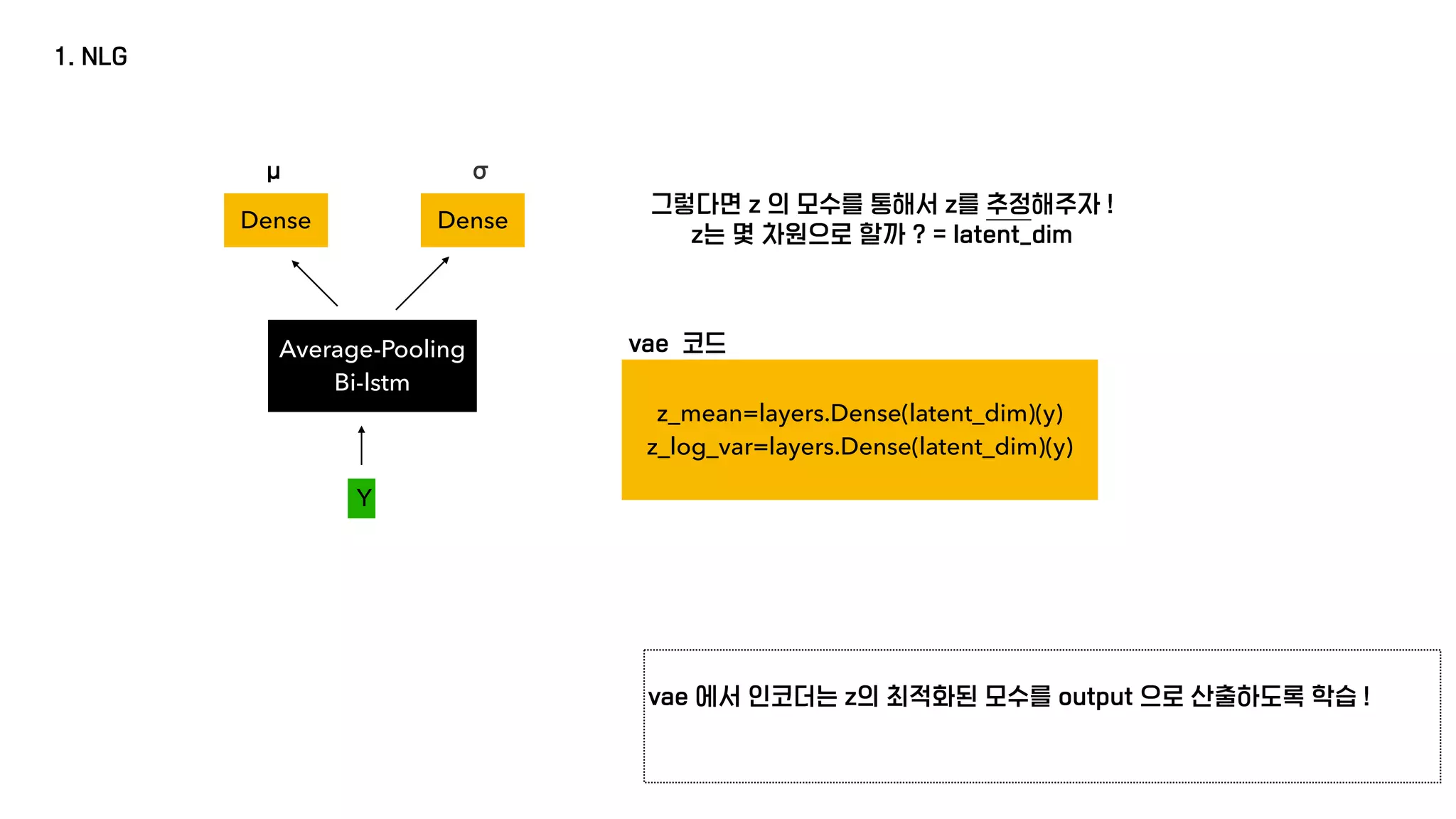
[ [μ 1 ,σ1],
[μ 2 ,σ2]]
[ [z1],
[z2]]
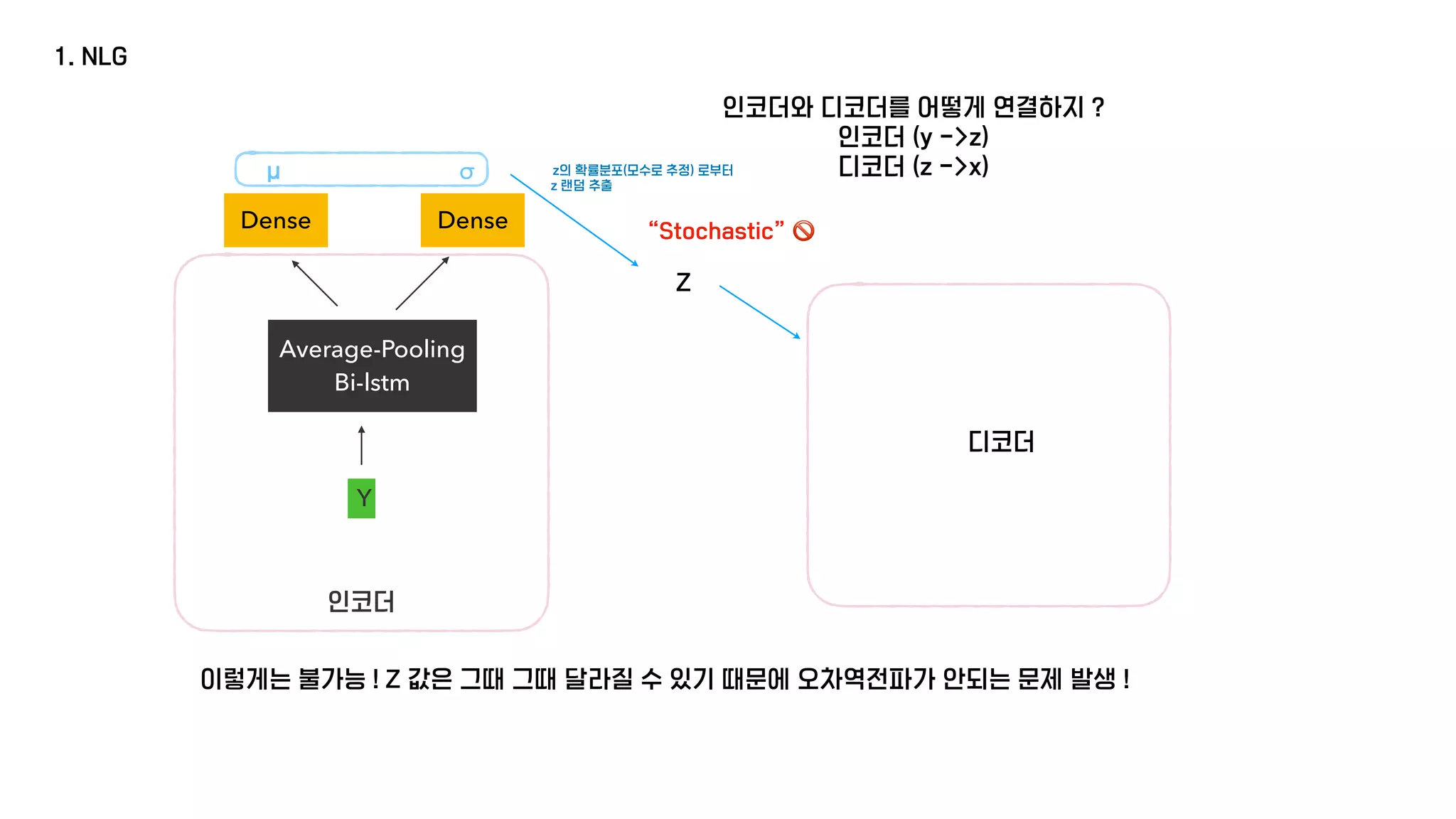
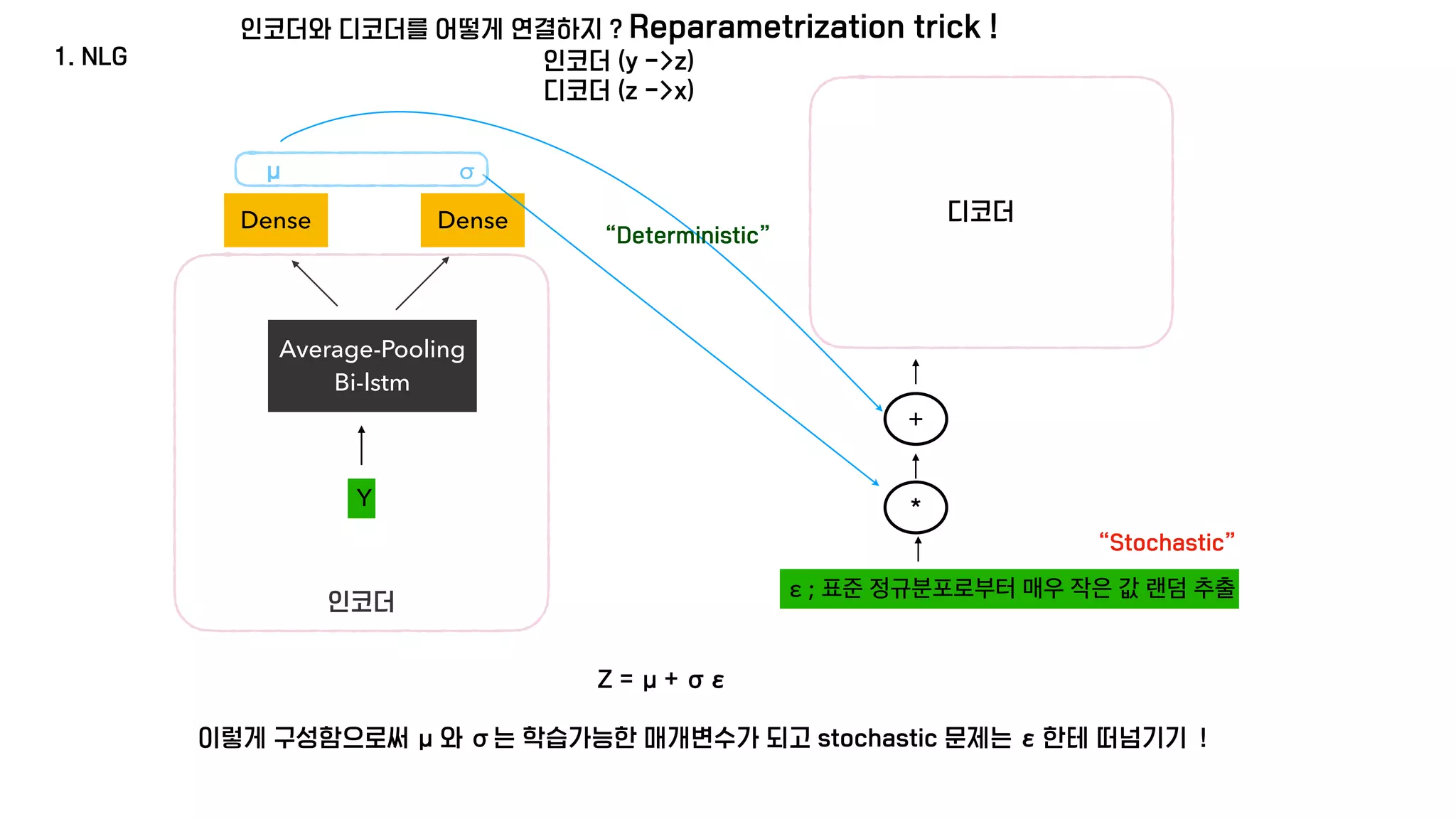
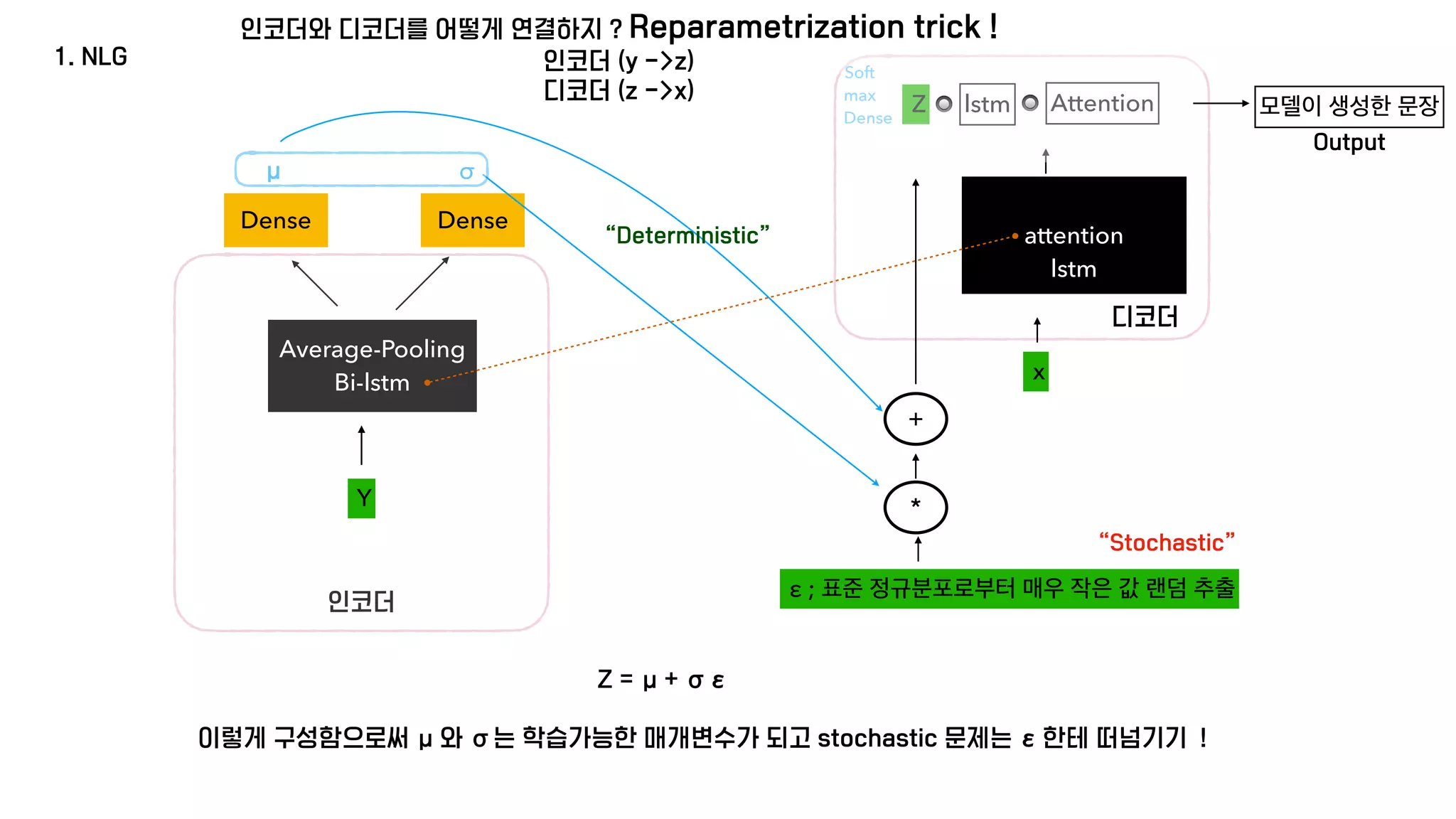
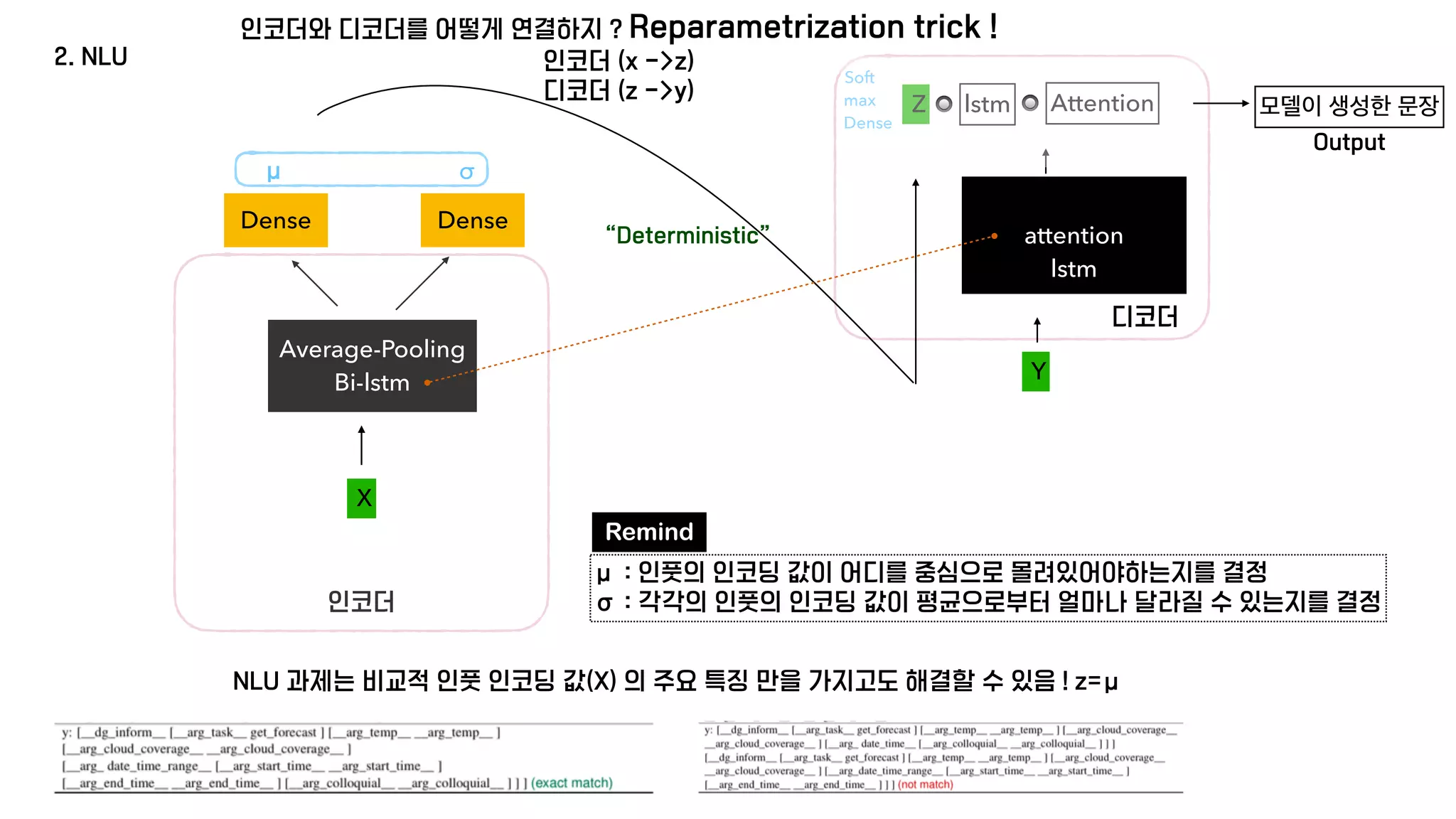
μ : 인풋의 인코딩 값이 어디를 중심으로 몰려있어야하는지를 결정
σ : 각각의 인풋의 인코딩 값이 평균으로부터 얼마나 달라질 수 있는지를 결정

12. 1. NLG
Y
인코더와 디코더를 어떻게 연결하지 ?
인코더 (y ->z)
디코더 (z ->x)
Average-Pooling
Bi-lstm
Dense Dense
μ σ
인코더
Z
z의 확률분포(모수로 추정) 로부터
z 랜덤 추출
디코더
이렇게는 불가능 ! Z 값은 그때 그때 달라질 수 있기 때문에 오차역전파가 안되는 문제 발생 !
“Stochastic” 🚫

13. 1. NLG
Y
인코더와 디코더를 어떻게 연결하지 ? Reparametrization trick !
인코더 (y ->z)
디코더 (z ->x)
Average-Pooling
Bi-lstm
Dense Dense
μ σ
인코더
디코더
Z = μ+ σε
Y
ε ; 표준 정규분포로부터 매우 작은 값 랜덤 추출
*
+
“Stochastic”
“Deterministic”
이렇게 구성함으로써 μ와 σ는 학습가능한 매개변수가 되고 stochastic 문제는 ε한테 떠넘기기 !

14. 1. NLG
Y
인코더와 디코더를 어떻게 연결하지 ? Reparametrization trick !
인코더 (y ->z)
디코더 (z ->x)
Average-Pooling
Bi-lstm
Dense Dense
μ σ
인코더
디코더
Z = μ+ σε
Y
ε ; 표준 정규분포로부터 매우 작은 값 랜덤 추출
*
+
“Stochastic”
“Deterministic”
이렇게 구성함으로써 μ와 σ는 학습가능한 매개변수가 되고 stochastic 문제는 ε한테 떠넘기기 !
attention
lstm
x
Z lstm Attention
Soft
max
Dense
모델이 생성한 문장
Output
🔘 🔘

15. Y (input) : “{name=giraffe,eat_type=restaurant,price_range=more than 30,near=the six bells}
X (output) : “For those prepared to pay over 30,giraffe is a restaurant located near the six bells”
인코더
디코더
giraffe restaurant more than 30 the six bells
For those …
NLG 에서 Weather dataset 의 encoder input 의
경우 tree structure(y) 를 linearize 해서 집어넣기 !

16. 2. NLU
Y
인코더와 디코더를 어떻게 연결하지 ? Reparametrization trick !
인코더 (x ->z)
디코더 (z ->y)
Average-Pooling
Bi-lstm
Dense Dense
μ σ
인코더
디코더
X
“Deterministic”
NLU 과제는 비교적 인풋 인코딩 값(X) 의 주요 특징 만을 가지고도 해결할 수 있음 ! z=μ
attention
lstm
Y
Z lstm Attention
Soft
max
Dense
모델이 생성한 문장
Output
🔘 🔘
μ : 인풋의 인코딩 값이 어디를 중심으로 몰려있어야하는지를 결정
σ : 각각의 인풋의 인코딩 값이 평균으로부터 얼마나 달라질 수 있는지를 결정
Remind

17. Y (input) : “{name=giraffe,eat_type=restaurant,price_range=more than 30,near=the six bells}
X (output) : “For those prepared to pay over 30,giraffe is a restaurant located near the six bells”
인코더
디코더
For those prepared to
name eat_type price_range
E2E 데이터셋의 경우 slot 1개 당 한 개의 classifier 존재
…
near
Giraffe
…
Elephant

18. 질문 있으신가요 ? 🙋🙋

19. 모델 최적화 방법 🧩
step by step

20. 은 수학,수학,수학으로 이루어졌더라구요 🙄

21. 지금부터 차근차근 살펴보아요 🌊

22. 1. 옌킨의 부등식

23. 2. KL-Divergence : 두 분포의 차이
1. p 분포를 따를 때 얻는
평균적인 정보량
2. 그런데 p분포가 아닌
q 분포를 따른다면
3. 정보량이
어떻게 달라질까 ?

24. 3. Marginalization
: A 변수 와 B 변수의 관계 (확률값 등등) 를 보고 싶은데, C 변수가 개입되어있다면 ?
모든 C 변수의 경우에서 A 변수와 B 변수의 관계를 구해줘야지 정확한 결과가 나옴 !
P(happiness|weather) = P(happiness, country=England | weather) + P(happiness, country=Scotland | weather) + P(happiness, country=Wales | weather)
A
B C

25. ⛳ P (Z | X,Y) 를 최대화시키기
MLE 방식 > P (X,Y| Z) 를 최대화시키기
여기서 잠깐 !
x 나 y 를 구할 때 z 가 관여

26. 복권에 대한 상금의 기댓값 :
상금 100 50 10
확률 1/1000 1/500 1/100
복권 종류에 따라서 상금이 당첨될 확률이 결정 !
100 * (1/1000) + 50 * (1/500) + 10 * (1/100)
샘플링한 z 에 대한 의 기댓값 :
Z ~
(X 값 고정, Y 값 고정) Z 값 = ?
확률 ?
…
z 에 따라서 값 각각이 나올 수 있는 확률이 결정

27. Remind
ELBO 가 커지면 log likelihood 값도 커지게 된다 👀 ELBO 를 최적화함수로 사용하자 !
ELBO
따라서, 최적화 함수는

28. 그런데 ! ⏪ ⏪
Z 를 X 를 통해서 구했다 !
따라서, NLU 모델 최적화 함수는
NLG 모델 최적화 함수는

29. X 만 주어진 경우나 Y 만 주어진 경우는 ?
⛳ P (Z | X) 를 최대화시키기
X 만 주어진 경우
MLE 방식 > P (X | Z) 를 최대화시키기
그런데 ! ⛳ 정확히 말하면 결국 X 데이터만 주어진 unsupervised 방식에서도 최적의 Y를 구하고 싶은 것 !
따라서 ! MLE 방식 > P (X x->z->y->z->x | Z) 를 최대화시키기
X 를 구할 때 Y,Z 가 관여 -> marginalize !

30. 각 경우별 최적화 함수 정리
1. (X,Y) labelled data 에서 NLU 성능 향상을 위한 Z 최적화
2. (X,Y) labelled data 에서 NLG 성능 향상을 위한 Z 최적화
3. (X,?) unlabelled data 에서 NLU 성능 향상을 위한 Z 최적화
4. (?,Y) unlabelled data 에서 NLU 성능 향상을 위한 Z 최적화

31. 그런데 ! ⏪ ⏪
x ; 자연어
하지만 현재 상태 (NLU 최적화는 주황색, NLG 최적화는 보라색)
잠재공간 z Y ; 컴퓨터가 이해한 방식
잠재공간 z
아이디어 1 ) prior 을 맞춰주자 !
q(z|x) = q(x|z) * p(z)
q(z|y) = q(y|z) * p(z)
하지만 NLU,NLG 모델의 최적화 함수가 달라서
공간이 좁혀지는 데에는 한계가 생김
prior 을 단순히 통일시키는 것이 아니라 prior 을 활용해서 두 공간을 연결 시키자 !
q(z|x) = q(x|z) * p(z|y)
q(z|y) = q(y|z) * p(z|x)
스포일러

32. 드디어 !

33. JUG 모델의 최적화 함수
1. (X,Y) labelled data 에서 NLU,NLG 성능 향상을 위한 Z 최적화
2. (X,Y) labelled data 에서 NLU,NLG 성능 향상을 위한 Z 최적화,
auto-encoding paths 최적화
3. 일부 unlabelled data 를 추가했을 때 NLU,NLG 성능 향상을 위한 Z 최적화
➕
➕
➕ ➕
➕
➕ ➕

34. 질문 있으신가요 ? 🙋🙋

35. 실험 및 결과 분석 🧐

36. JUG model vs 기존 NLU, NLG 모델
치트키 :
JUG semi
치트키 :
Augmentation
Augmentation :
1) 단일 NLU,NLG 모델을 unlabelled data 로
pre-training , 이를 통해 labelled data 생성(;labelled data2)
2) 기존에 존재하는 labelled data1에 labelled data2 까지 추가하여
1)의 단일 모델 fine-tuning

37. JUG basic vs 기존 NLU, NLG 모델
NLU, NLG 모델 각각에서
성능이 고르게 우수 !

38. JUG vs 기존 NLU, NLG 모델
단일 모델(Decoupled) 도 치트키인
Augmentation 에서는 성능이 향상하였지만 그래도
JUG 모델의 성능에는 못 미침
JUG semi 모델 💯 ! 특히 labelled data 의 비율이
적은 경우 결과가 매우 유의미 -> 데이터 수가
부족한 경우에 JUG 모델이 잘 활용될 가능성을 보임

39. 공유 공간 Z 의 빈 자리가 얼마나 클까 ?

40. X 데이터 셋 vs Y 데이터 셋
Z 는 shared latent space 이기 때문에 bi-unlabelled data 를 사용했을 때
제일 효과적

41. 질문 있으신가요 ? 🙋🙋

42. 연관된 연구 🗂

43. Auto-encoder
🚂
https://arxiv.org/pdf/2003.05991.pdf
Vae
🚗
https://arxiv.org/pdf/1312.6114.pdf

44. vae 코드
def vae_loss(x, x_decoded_mean):
xent_loss = objectives.binary_crossentropy(x,
x_decoded_mean)
kl_loss = -0.5 * K.mean(1 + z_log_var -
K.square(z_mean) - K.exp(z_log_var))
loss = xent_loss + kl_loss
return loss

45. 질문 있으신가요 ? 🙋🙋

46. 감사합니다 ! 🌝
발표 자료가 필요하시면 337jenny79@gmail.com 으로 연락 주세요