This document discusses optimization and recognition problems related to permutation graphs, outlining techniques such as dynamic programming and modular decompositions. It includes definitions, basic properties, and theorems on how to solve various graph-related problems efficiently. The conclusion raises questions about the complexity of related problems in this field.

1. Introduction Optimization problems Recognition Encoding all realizers Conclusion
Permutation graphs — an introduction
Ioan Todinca
LIFO - Universit´ d’Orl´ans
e e
Algorithms and permutations, february 2012
1/14

2. Introduction Optimization problems Recognition Encoding all realizers Conclusion
Permutation graphs
1 2 3 4
1
0 1
0 1
0 11
00
1
0 1
0 1
0 11
00 2
3 4
1
1
0 1
0 5
1
0 1
0 6
5 6
• Optimisation algorithms
use, as input, the intersection model (realizer)
• Recognition algorithms
output the intersection(s) model(s)
2/14

3. Introduction Optimization problems Recognition Encoding all realizers Conclusion
Plan of the talk
1. Relationship with other graph classes
2. Optimisation problems :
MaxIndependentSet/MaxClique/Coloring ;
Treewidth
3. Recognition algorithm
4. Encoding all realizers via modular decomposition
5. Conclusion
3/14

4. Introduction Optimization problems Recognition Encoding all realizers Conclusion
Definition and basic properties
2 1 6 5 4 3
1 2 3 4 2
1
0 1
0 1
0 11
00
1
0 1
0 1
0 11
00 3 4
1
5 6
1
0 1
0
1
0 1
0
5 6 1 5 6 3 2 4
• Realizer : (π1 , π2 )
• One can ”reverse” the realizer upside-down or right-left :
(π1 , π2 ) ∼ (π2 , π1 ) ∼ (π1 , π2 ) ∼ (π2 , π1 )
• Complements of permutation graphs are permutation graphs.
→ Reverse the ordering of the bottoms of the segments :
(π1 , π2 ) → (π1 , π2 )
4/14

5. Introduction Optimization problems Recognition Encoding all realizers Conclusion
Definition and basic properties
2 1 6 5 4 3
1 2 3 4
1
0 1
0 1
0 11
00
1
0 1
0 1
0 11
00
1
0 1
0
1
0 1
0
5 6 1 5 6 3 2 4
• Realizer : (π1 , π2 )
• One can ”reverse” the realizer upside-down or right-left :
(π1 , π2 ) ∼ (π2 , π1 ) ∼ (π1 , π2 ) ∼ (π2 , π1 )
• Complements of permutation graphs are permutation graphs.
→ Reverse the ordering of the bottoms of the segments :
(π1 , π2 ) → (π1 , π2 )
4/14

6. Introduction Optimization problems Recognition Encoding all realizers Conclusion
Definition and basic properties
2 1 6 5 4 3
1 2 3 4
1
0 1
0 1
0 11
00
1
0 1
0 1
0 11
00
1
0 1
0
1
0 1
0
5 6 4 2 3 6 5 1
• Realizer : (π1 , π2 )
• One can ”reverse” the realizer upside-down or right-left :
(π1 , π2 ) ∼ (π2 , π1 ) ∼ (π1 , π2 ) ∼ (π2 , π1 )
• Complements of permutation graphs are permutation graphs.
→ Reverse the ordering of the bottoms of the segments :
(π1 , π2 ) → (π1 , π2 )
4/14

7. Introduction Optimization problems Recognition Encoding all realizers Conclusion
Definition and basic properties
2 1 6 5 4 3
1 2 3 4
1
0 1
0 1
0 11
00
1
0 1
0 1
0 11
00
1
0 1
0
1
0 1
0
5 6 4 2 3 6 5 1
• Realizer : (π1 , π2 )
• One can ”reverse” the realizer upside-down or right-left :
(π1 , π2 ) ∼ (π2 , π1 ) ∼ (π1 , π2 ) ∼ (π2 , π1 )
• Complements of permutation graphs are permutation graphs.
→ Reverse the ordering of the bottoms of the segments :
(π1 , π2 ) → (π1 , π2 )
4/14

8. Introduction Optimization problems Recognition Encoding all realizers Conclusion
More intersection graph classes
Circle graphs Trapezoid graphs
Books on graph classes : [Golumbic ’80 ; Brandst¨dt, Le, Spinrad
a
’99 ; Spinrad 2003]
5/14

9. Introduction Optimization problems Recognition Encoding all realizers Conclusion
MaxIndependentSet via Dynamic Programming
1 2 3 4 5 6
2 4 3 6 1 5
• Dynamic programming from left to right :
MIS[i] = 1 + max MIS[j]
j left to i
• MaxIndependentSet corresponds to the longest increasing
sequence in a permutation — O(n log n)
• MaxClique : longest decreasing sequence
• Coloring : chromatic number = max clique (perfect graphs)
6/14

10. Introduction Optimization problems Recognition Encoding all realizers Conclusion
Treewidth via dynamic programming on scanlines
1 2 3 4
1
0
1
0 1
0
1
0 1
0
1
0 11
00
11
00 2 1 6 5 4 3
1
0 1
0
1
0 1
0
5 6
12 256 23 34
1 5 6 3 2 4
• Minimal separators correspond to scanlines
• Bags correspond to areas between two scanlines
• Treewidth can be solved in polynomial time [Bodlaender,
Kloks, Kratsch 95 ; Meister 2010]
7/14

11. Introduction Optimization problems Recognition Encoding all realizers Conclusion
Treewidth via dynamic programming on scanlines
1 2 3 4
1
0
1
0 1
0
1
0 1
0
1
0 11
00
11
00 2 1 6 5 4 3
1
0 1
0
1
0 1
0
5 6
12 256 23 34
1 5 6 3 2 4
• Minimal separators correspond to scanlines
• Bags correspond to areas between two scanlines
• Treewidth can be solved in polynomial time [Bodlaender,
Kloks, Kratsch 95 ; Meister 2010]
7/14

12. Introduction Optimization problems Recognition Encoding all realizers Conclusion
Treewidth via dynamic programming on scanlines
1 2 3 4
1
0
1
0 1
0
1
0 1
0
1
0 11
00
11
00 2 1 6 5 4 3
1
0 1
0
1
0 1
0
5 6
12 256 23 34
1 5 6 3 2 4
• Minimal separators correspond to scanlines
• Bags correspond to areas between two scanlines
• Treewidth can be solved in polynomial time [Bodlaender,
Kloks, Kratsch 95 ; Meister 2010]
7/14

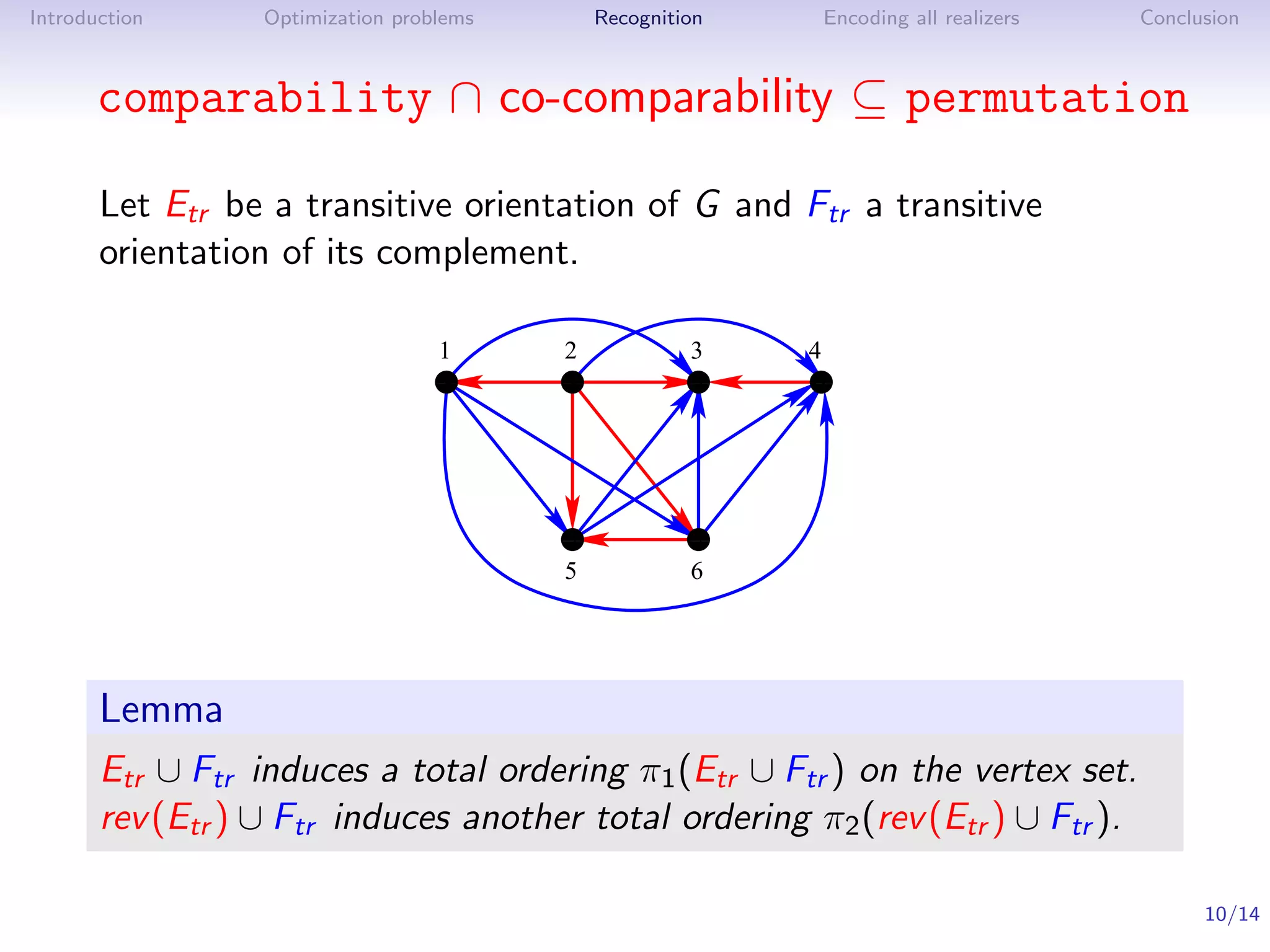
13. Introduction Optimization problems Recognition Encoding all realizers Conclusion
Recognition algorithm
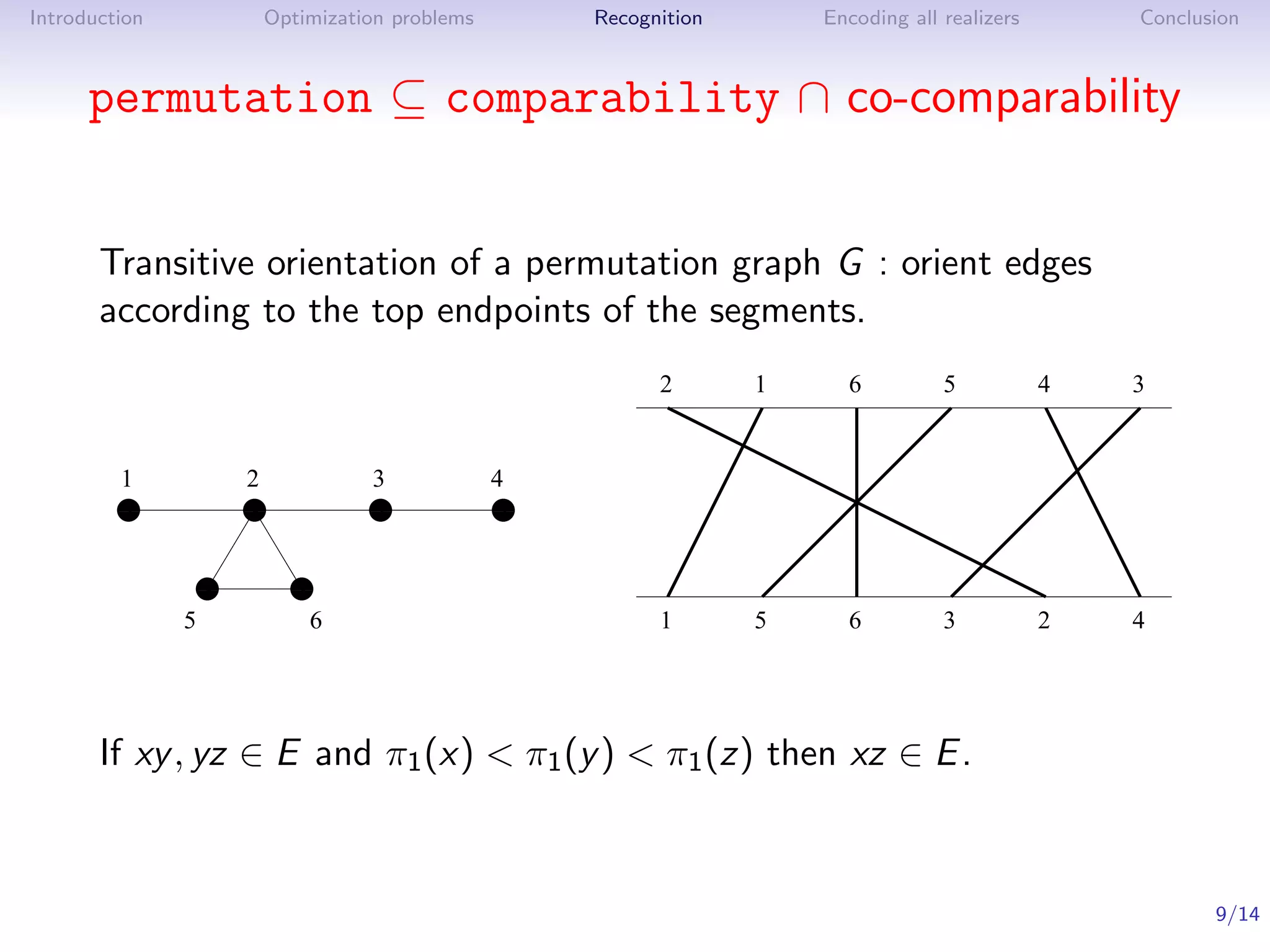
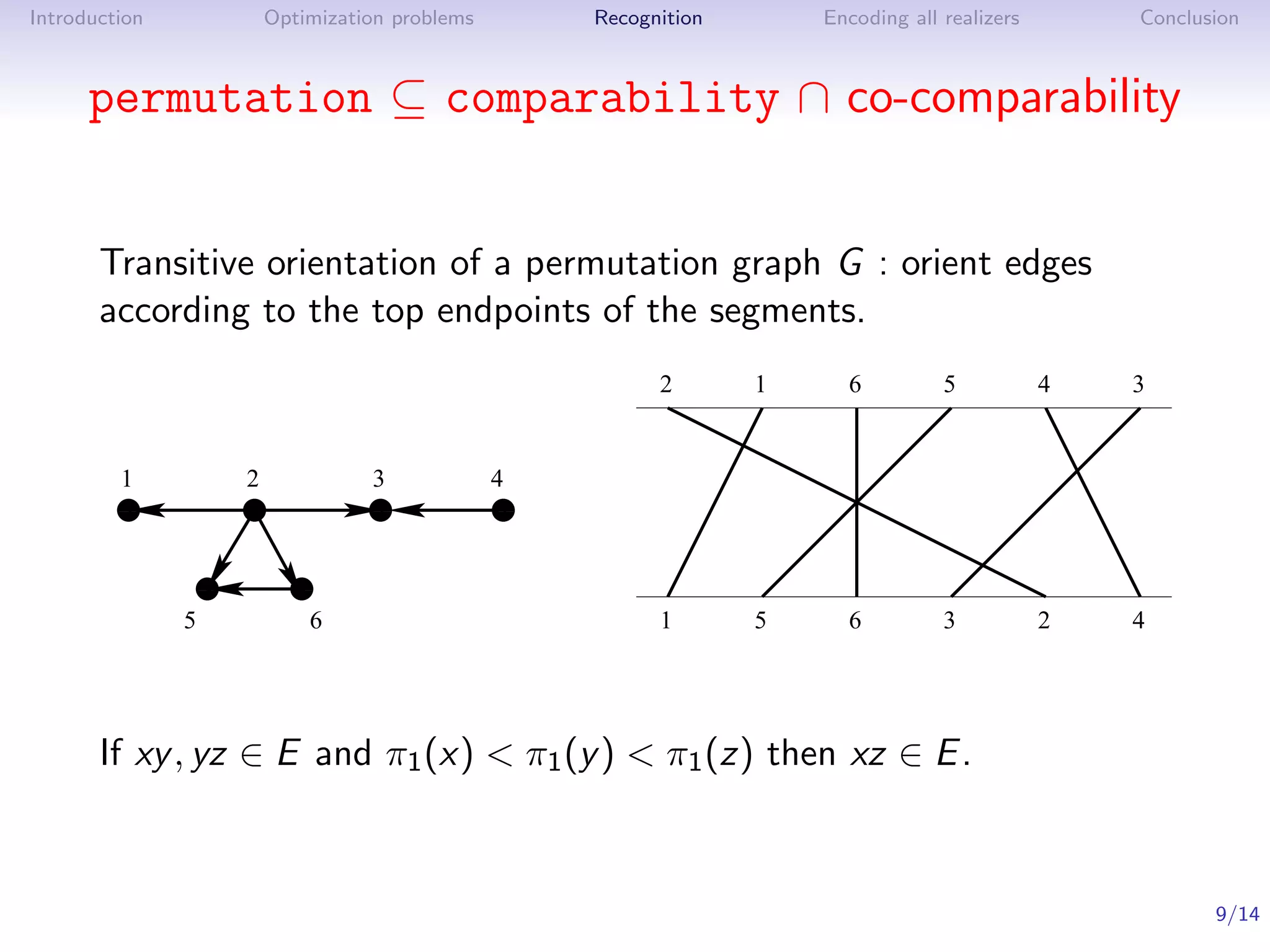
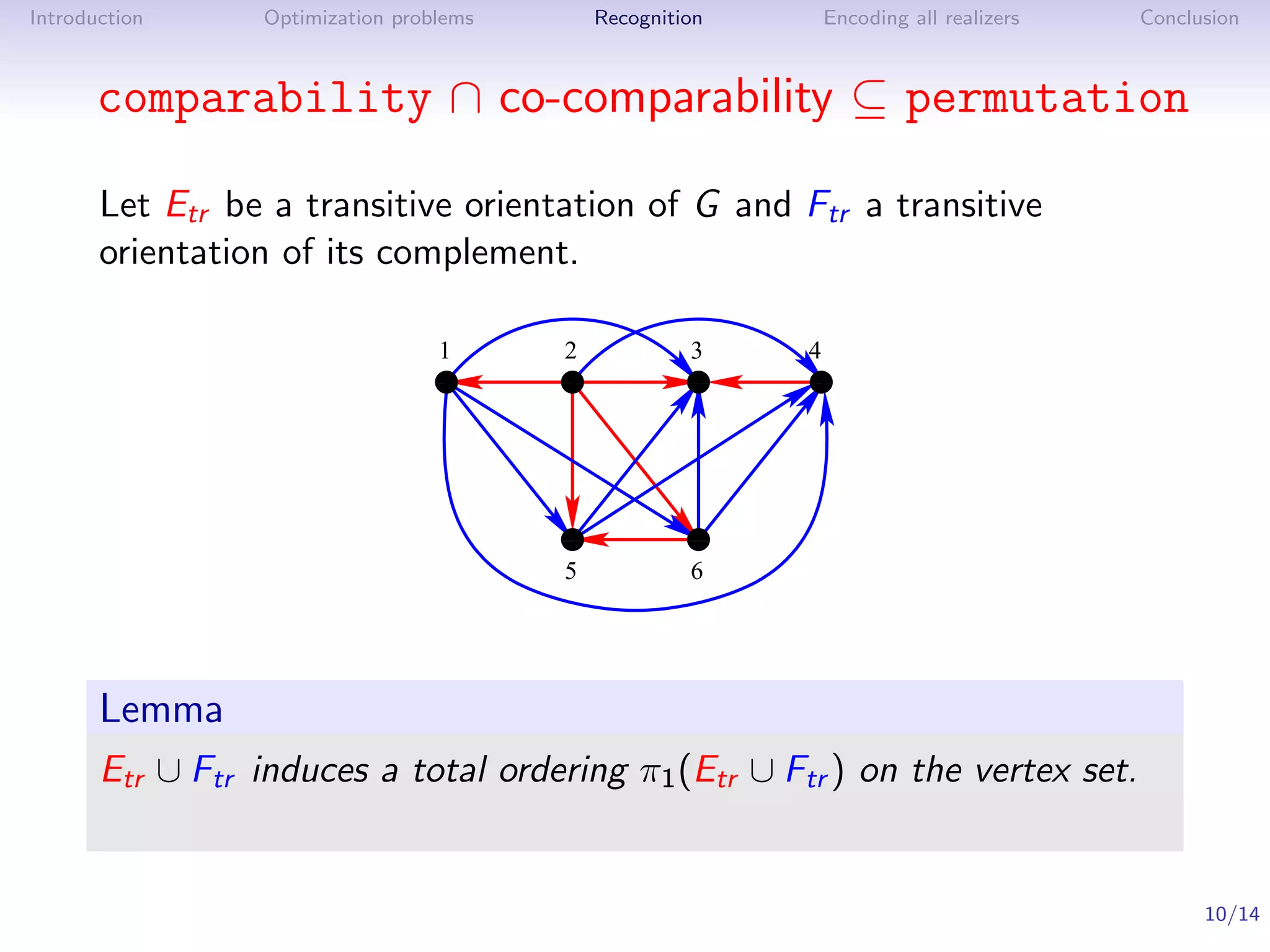
Theorem ([Pnueli, Lempel, Even ’71], see also [Golumbic ’80])
G is a permutation graph if and only if G and G are comparability
graphs.
Algorithm
1. Find a transitive orientation of G and one of G
2. Construct an intersection model for G
In O(n + m) time by [McConnell, Spinrad ’99]
8/14

14. Introduction Optimization problems Recognition Encoding all realizers Conclusion
permutation ⊆ comparability ∩ co-comparability
Transitive orientation of a permutation graph G : orient edges
according to the top endpoints of the segments.
2 1 6 5 4 3
1 2 3 4
1
0 1
0 1
0 11
00
1
0 1
0 1
0 11
00
1
0
1
0 1
0
1
0
5 6 1 5 6 3 2 4
If xy , yz ∈ E and π1 (x) < π1 (y ) < π1 (z) then xz ∈ E .
9/14

15. Introduction Optimization problems Recognition Encoding all realizers Conclusion
permutation ⊆ comparability ∩ co-comparability
Transitive orientation of a permutation graph G : orient edges
according to the top endpoints of the segments.
2 1 6 5 4 3
1 2 3 4
1
0 1
0 1
0 11
00
1
0 1
0 1
0 11
00
1
0
1
0 1
0
1
0
5 6 1 5 6 3 2 4
If xy , yz ∈ E and π1 (x) < π1 (y ) < π1 (z) then xz ∈ E .
9/14

16. Introduction Optimization problems Recognition Encoding all realizers Conclusion
comparability ∩ co-comparability ⊆ permutation
Let Etr be a transitive orientation of G and Ftr a transitive
orientation of its complement.
1 2 3 4
1
0
1
0 1
0
1
0 1
0
1
0 11
00
11
00
1
0 1
0
1
0 1
0
5 6
Lemma
Etr ∪ Ftr induces a total ordering π1 (Etr ∪ Ftr ) on the vertex set.
10/14

17. Introduction Optimization problems Recognition Encoding all realizers Conclusion
comparability ∩ co-comparability ⊆ permutation
Let Etr be a transitive orientation of G and Ftr a transitive
orientation of its complement.
1 2 3 4
1
0
1
0 1
0
1
0 1
0
1
0 11
00
11
00
1
0 1
0
1
0 1
0
5 6
Lemma
Etr ∪ Ftr induces a total ordering π1 (Etr ∪ Ftr ) on the vertex set.
rev (Etr ) ∪ Ftr induces another total ordering π2 (rev (Etr ) ∪ Ftr ).
10/14

18. Introduction Optimization problems Recognition Encoding all realizers Conclusion
A realizer of G
Permutations π1 (Etr ∪ Ftr ) and π2 (rev (Etr ) ∪ Ftr ) form a realizer
of G .
2 1 6 5 4 3
1 2 3 4
1
0 1
0 1
0 11
00
1
0 1
0 1
0 11
00
1
0
1
0 1
0
1
0
1 5 6 3 2 4 5 6
Segments x and y intersect iff (xy ) ∈ Etr and (yx) ∈ rev (Etr ) or
vice-versa ; equivalently, iff xy ∈ E .
11/14

19. Introduction Optimization problems Recognition Encoding all realizers Conclusion
Modules and common intervals
• Substituting a segment (vertex) by the realizer of a
permutation graph (module) produces a new permutation
graph.
• A common interval of π1 and π2 forms a module in G
• Strong modules correspond exactly to strong common
intervals [de Mongolfier 2003]
• A graph is a permutation graphs iff all prime nodes in the
modular decomposition are permutation graphs.
12/14

20. Introduction Optimization problems Recognition Encoding all realizers Conclusion
Modules and common intervals
• Substituting a segment (vertex) by the realizer of a
permutation graph (module) produces a new permutation
graph.
• A common interval of π1 and π2 forms a module in G
• Strong modules correspond exactly to strong common
intervals [de Mongolfier 2003]
• A graph is a permutation graphs iff all prime nodes in the
modular decomposition are permutation graphs.
12/14

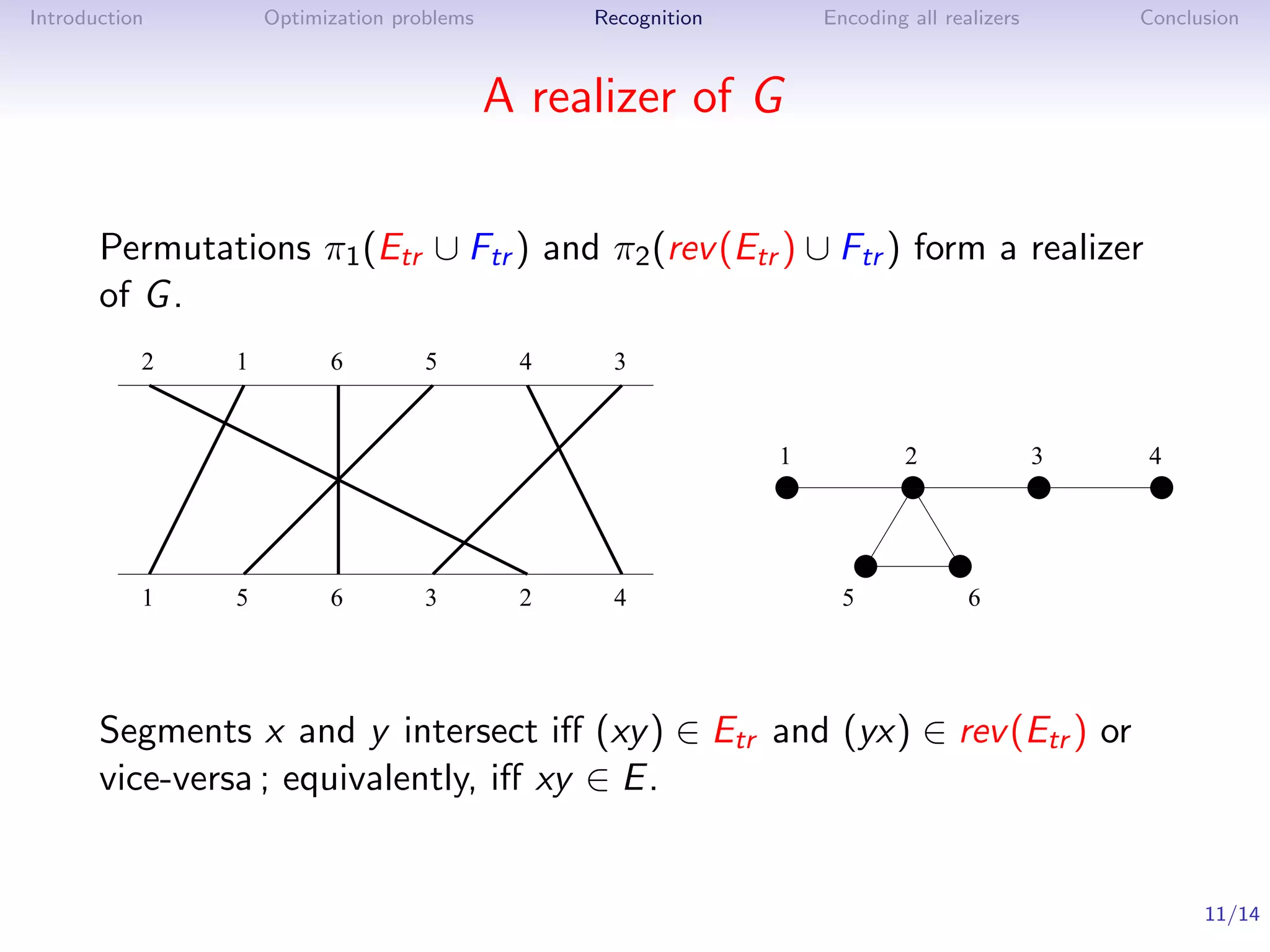
21. Introduction Optimization problems Recognition Encoding all realizers Conclusion
Encoding realizers
1 2 3 4
1
0 1
0 1
0 11
00
1
0 1
0 1
0 11
00
1
0 1
0
Theorem ([Gallai ’67]) 1
0 1
0
5 6
A prime permutation graph has a
unique realizer, up to reversals. prime
1 2 4
3
The modular decomposition tree
+ realizers of prime nodes
parallel 2 3 4
encode all possible realizers of G ,
cf. [Crespelle, Paul 2010].
series 1
5 6
13/14

22. Introduction Optimization problems Recognition Encoding all realizers Conclusion
Conclusion
Summary
• Many optimization problems become polynomial on
permutation graphs
• Representations (intersection models) based on modular
decompositions
Some questions
• Is Bandwidth polynomial or NP-complete on permutation
graphs ?
• What about subgraph isomorphism from parametrized point
of view ?
14/14

23. Introduction Optimization problems Recognition Encoding all realizers Conclusion
Conclusion
Summary
• Many optimization problems become polynomial on
permutation graphs
• Representations (intersection models) based on modular
decompositions
Some questions
• Is Bandwidth polynomial or NP-complete on permutation
graphs ?
• What about subgraph isomorphism from parametrized point
of view ?
Thank you ! Your questions ?
14/14