This document discusses optimization and recognition problems related to permutation graphs, outlining techniques such as dynamic programming and modular decompositions. It includes definitions, basic properties, and theorems on how to solve various graph-related problems efficiently. The conclusion raises questions about the complexity of related problems in this field.






![Introduction Optimization problems Recognition Encoding all realizers Conclusion
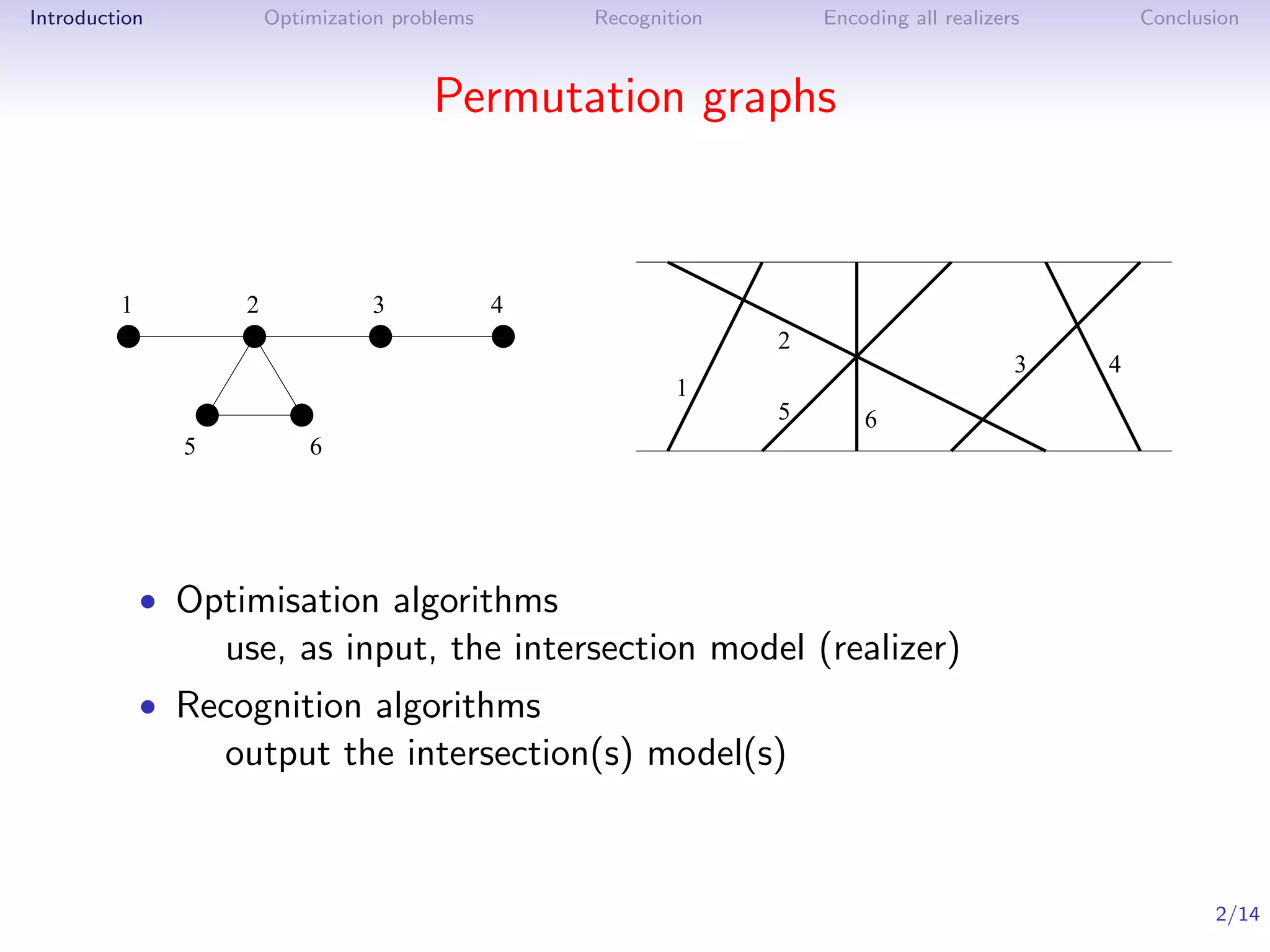
More intersection graph classes
Circle graphs Trapezoid graphs
Books on graph classes : [Golumbic ’80 ; Brandst¨dt, Le, Spinrad
a
’99 ; Spinrad 2003]
5/14](https://image.slidesharecdn.com/05todinca-120623180553-phpapp01/75/AlgoPerm2012-05-Ioan-Todinca-8-2048.jpg)
![Introduction Optimization problems Recognition Encoding all realizers Conclusion
MaxIndependentSet via Dynamic Programming
1 2 3 4 5 6
2 4 3 6 1 5
• Dynamic programming from left to right :
MIS[i] = 1 + max MIS[j]
j left to i
• MaxIndependentSet corresponds to the longest increasing
sequence in a permutation — O(n log n)
• MaxClique : longest decreasing sequence
• Coloring : chromatic number = max clique (perfect graphs)
6/14](https://image.slidesharecdn.com/05todinca-120623180553-phpapp01/75/AlgoPerm2012-05-Ioan-Todinca-9-2048.jpg)
![Introduction Optimization problems Recognition Encoding all realizers Conclusion
Treewidth via dynamic programming on scanlines
1 2 3 4
1
0
1
0 1
0
1
0 1
0
1
0 11
00
11
00 2 1 6 5 4 3
1
0 1
0
1
0 1
0
5 6
12 256 23 34
1 5 6 3 2 4
• Minimal separators correspond to scanlines
• Bags correspond to areas between two scanlines
• Treewidth can be solved in polynomial time [Bodlaender,
Kloks, Kratsch 95 ; Meister 2010]
7/14](https://image.slidesharecdn.com/05todinca-120623180553-phpapp01/75/AlgoPerm2012-05-Ioan-Todinca-10-2048.jpg)
![Introduction Optimization problems Recognition Encoding all realizers Conclusion
Treewidth via dynamic programming on scanlines
1 2 3 4
1
0
1
0 1
0
1
0 1
0
1
0 11
00
11
00 2 1 6 5 4 3
1
0 1
0
1
0 1
0
5 6
12 256 23 34
1 5 6 3 2 4
• Minimal separators correspond to scanlines
• Bags correspond to areas between two scanlines
• Treewidth can be solved in polynomial time [Bodlaender,
Kloks, Kratsch 95 ; Meister 2010]
7/14](https://image.slidesharecdn.com/05todinca-120623180553-phpapp01/75/AlgoPerm2012-05-Ioan-Todinca-11-2048.jpg)
![Introduction Optimization problems Recognition Encoding all realizers Conclusion
Treewidth via dynamic programming on scanlines
1 2 3 4
1
0
1
0 1
0
1
0 1
0
1
0 11
00
11
00 2 1 6 5 4 3
1
0 1
0
1
0 1
0
5 6
12 256 23 34
1 5 6 3 2 4
• Minimal separators correspond to scanlines
• Bags correspond to areas between two scanlines
• Treewidth can be solved in polynomial time [Bodlaender,
Kloks, Kratsch 95 ; Meister 2010]
7/14](https://image.slidesharecdn.com/05todinca-120623180553-phpapp01/75/AlgoPerm2012-05-Ioan-Todinca-12-2048.jpg)
![Introduction Optimization problems Recognition Encoding all realizers Conclusion
Recognition algorithm
Theorem ([Pnueli, Lempel, Even ’71], see also [Golumbic ’80])
G is a permutation graph if and only if G and G are comparability
graphs.
Algorithm
1. Find a transitive orientation of G and one of G
2. Construct an intersection model for G
In O(n + m) time by [McConnell, Spinrad ’99]
8/14](https://image.slidesharecdn.com/05todinca-120623180553-phpapp01/75/AlgoPerm2012-05-Ioan-Todinca-13-2048.jpg)
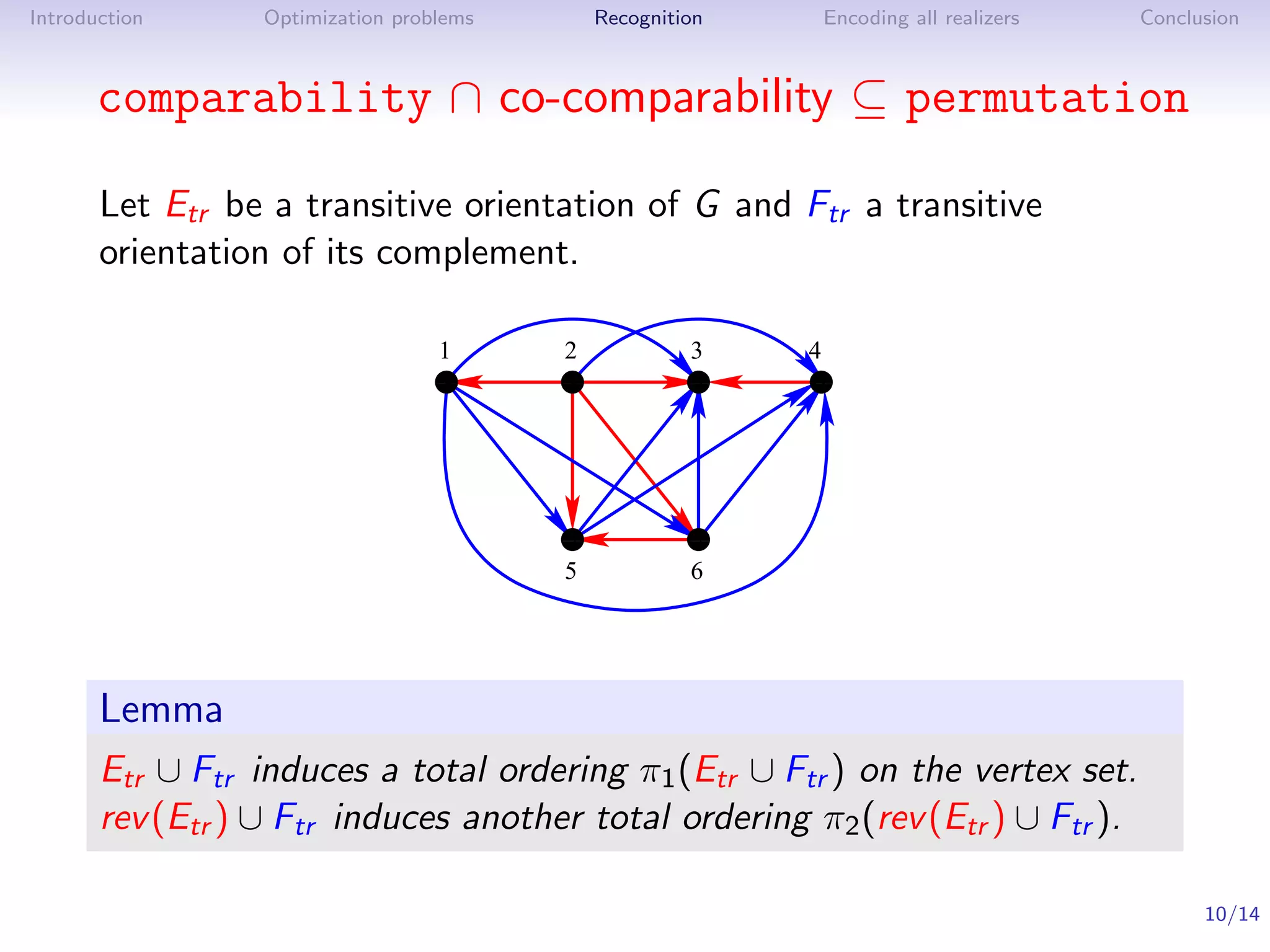
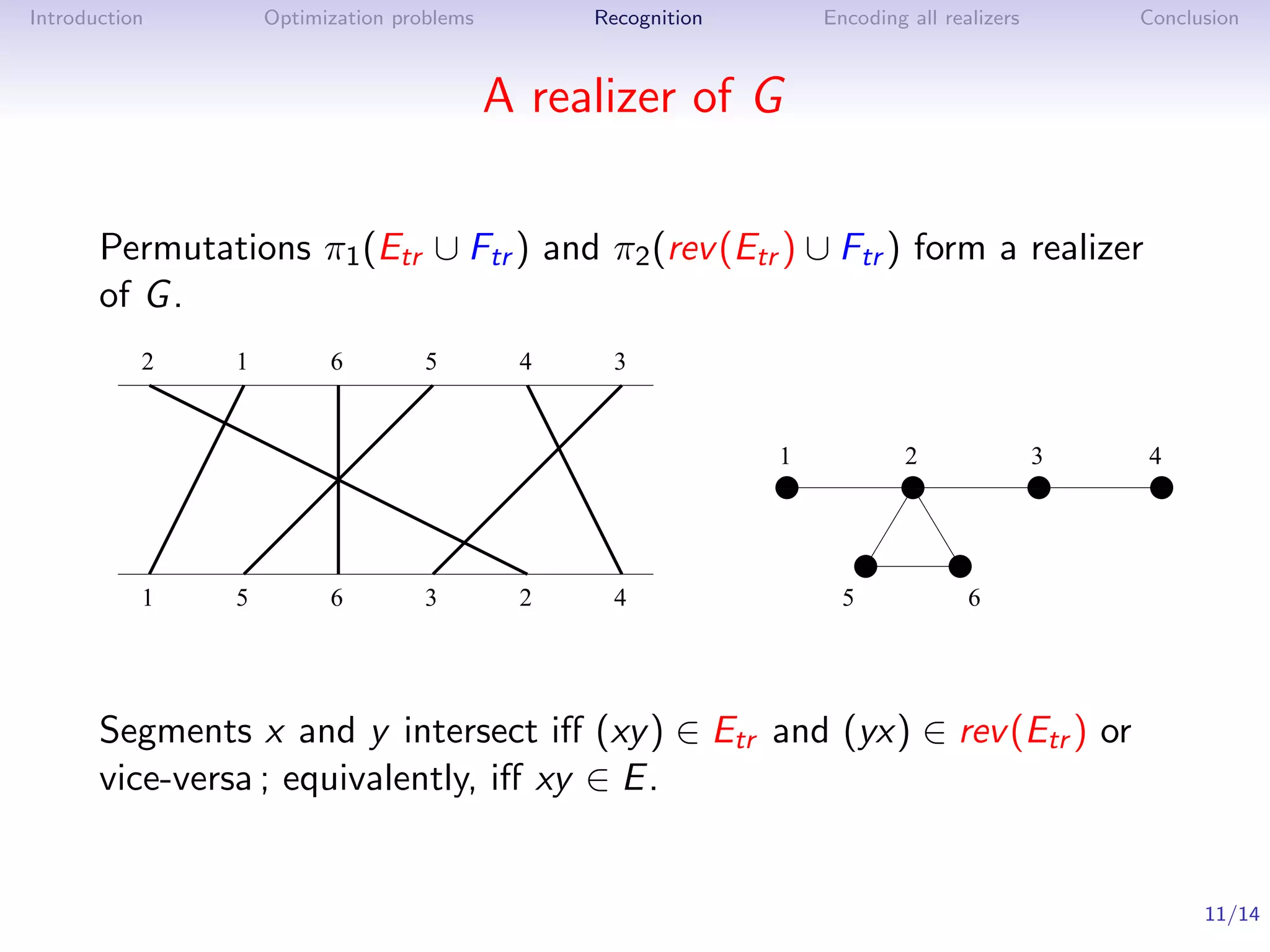
![Introduction Optimization problems Recognition Encoding all realizers Conclusion
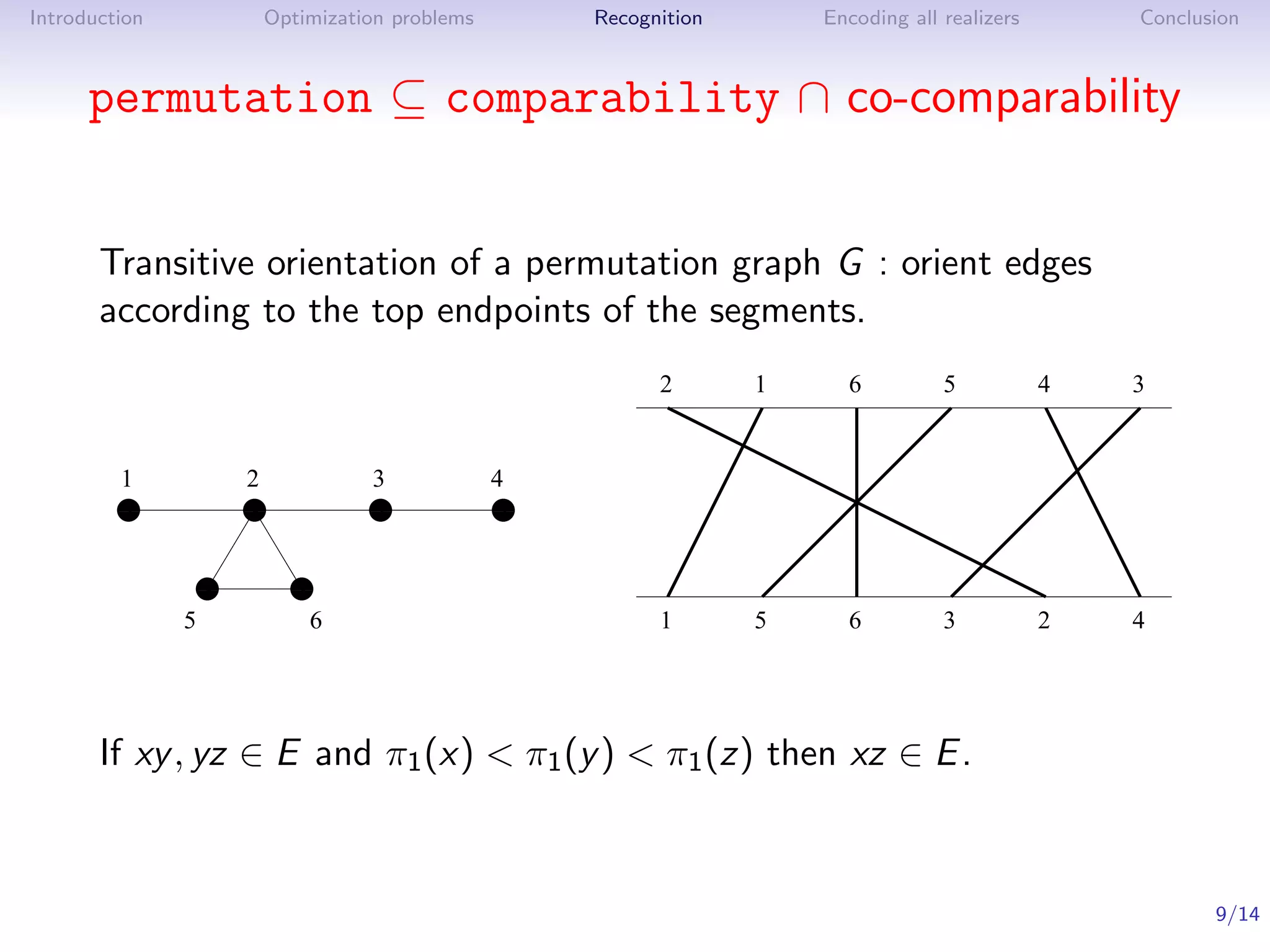
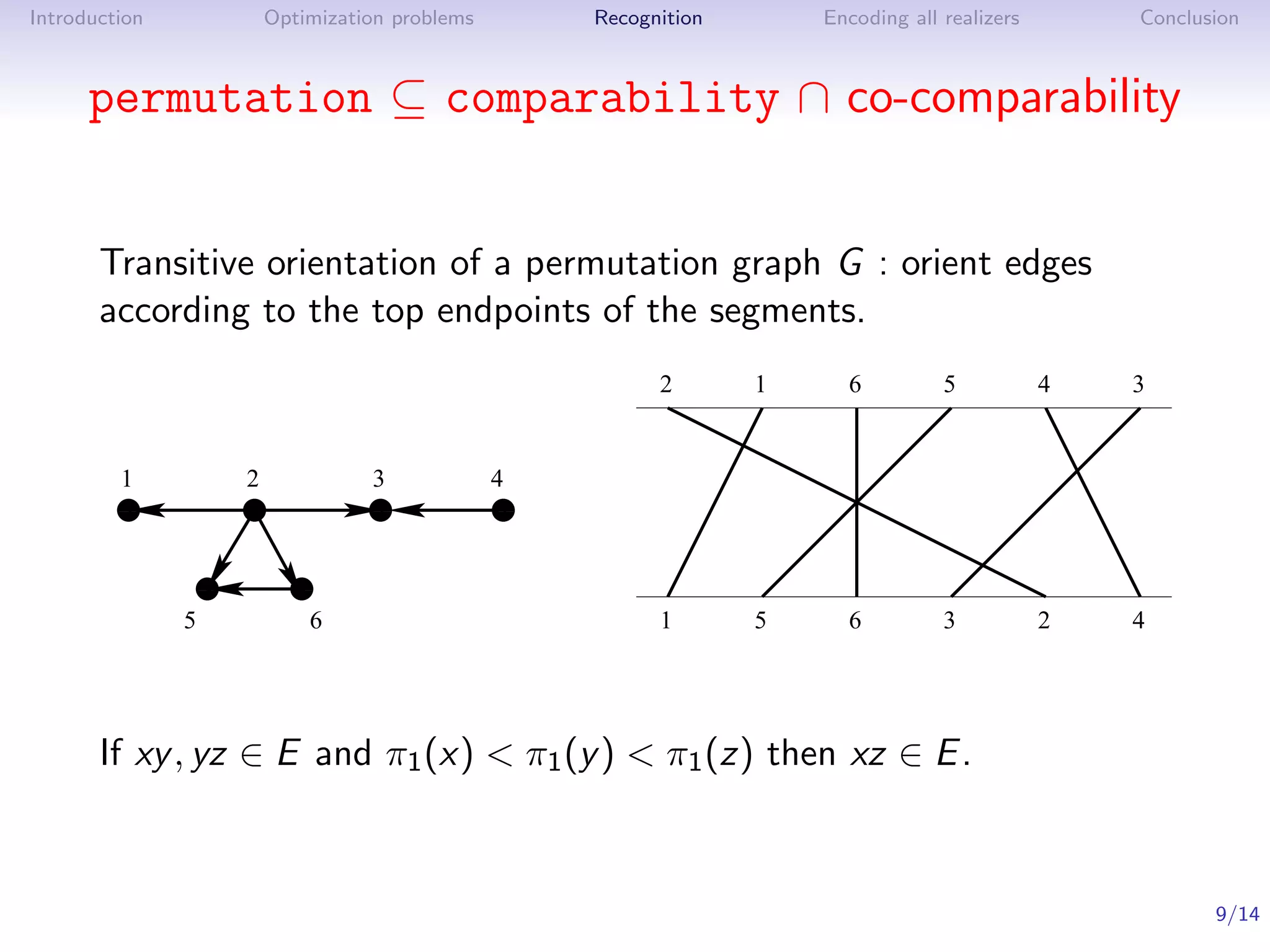
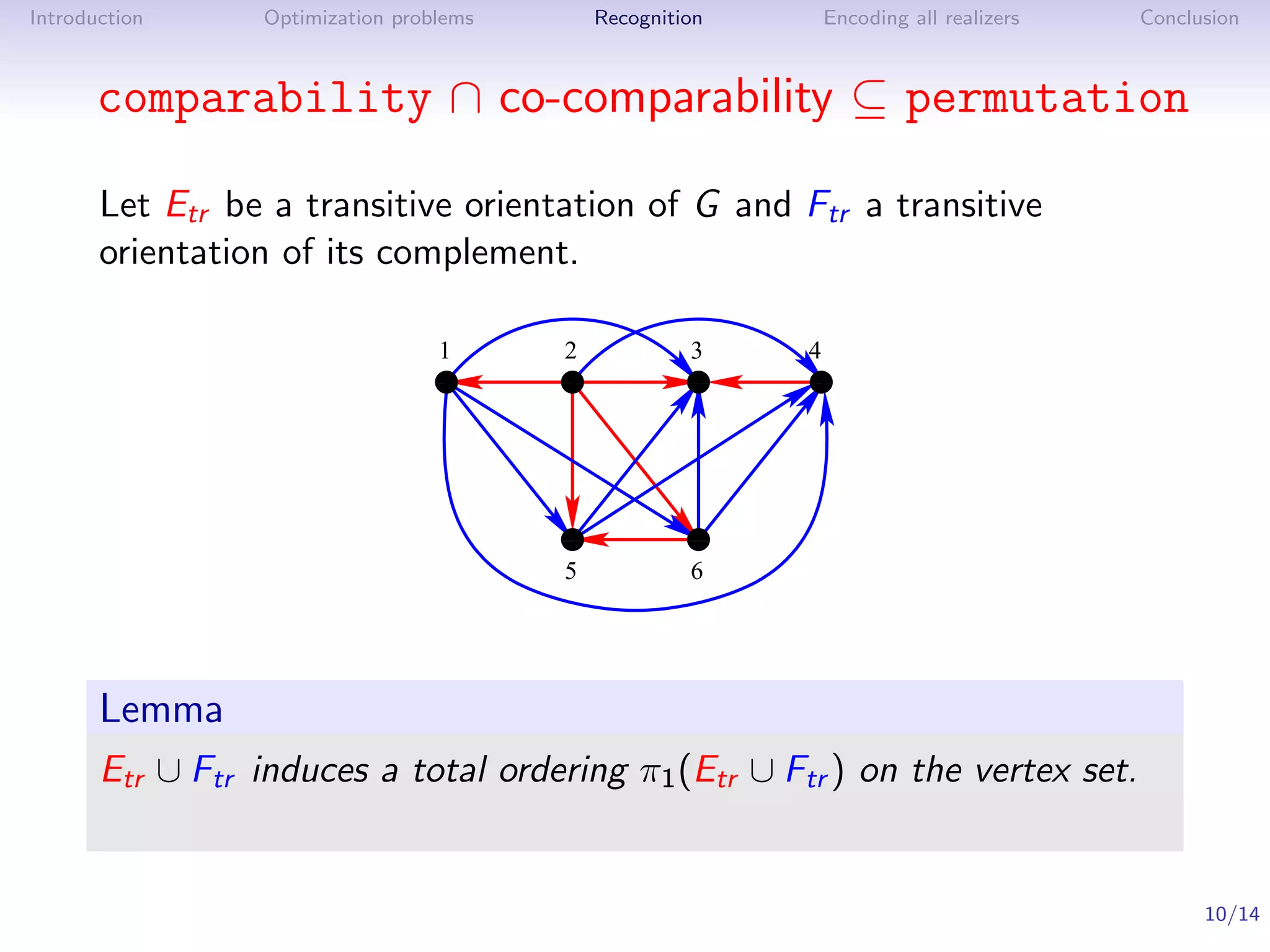
Modules and common intervals
• Substituting a segment (vertex) by the realizer of a
permutation graph (module) produces a new permutation
graph.
• A common interval of π1 and π2 forms a module in G
• Strong modules correspond exactly to strong common
intervals [de Mongolfier 2003]
• A graph is a permutation graphs iff all prime nodes in the
modular decomposition are permutation graphs.
12/14](https://image.slidesharecdn.com/05todinca-120623180553-phpapp01/75/AlgoPerm2012-05-Ioan-Todinca-19-2048.jpg)
![Introduction Optimization problems Recognition Encoding all realizers Conclusion
Modules and common intervals
• Substituting a segment (vertex) by the realizer of a
permutation graph (module) produces a new permutation
graph.
• A common interval of π1 and π2 forms a module in G
• Strong modules correspond exactly to strong common
intervals [de Mongolfier 2003]
• A graph is a permutation graphs iff all prime nodes in the
modular decomposition are permutation graphs.
12/14](https://image.slidesharecdn.com/05todinca-120623180553-phpapp01/75/AlgoPerm2012-05-Ioan-Todinca-20-2048.jpg)
![Introduction Optimization problems Recognition Encoding all realizers Conclusion
Encoding realizers
1 2 3 4
1
0 1
0 1
0 11
00
1
0 1
0 1
0 11
00
1
0 1
0
Theorem ([Gallai ’67]) 1
0 1
0
5 6
A prime permutation graph has a
unique realizer, up to reversals. prime
1 2 4
3
The modular decomposition tree
+ realizers of prime nodes
parallel 2 3 4
encode all possible realizers of G ,
cf. [Crespelle, Paul 2010].
series 1
5 6
13/14](https://image.slidesharecdn.com/05todinca-120623180553-phpapp01/75/AlgoPerm2012-05-Ioan-Todinca-21-2048.jpg)

