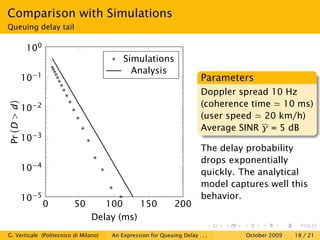
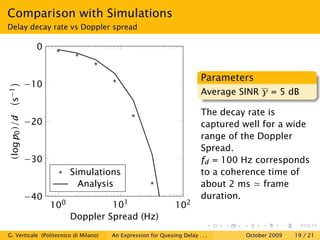
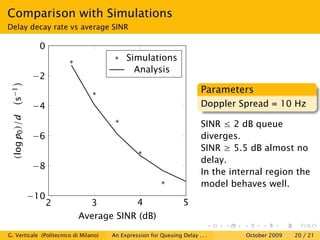
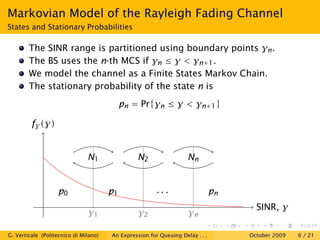
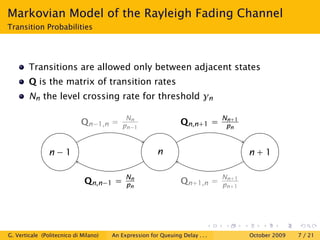
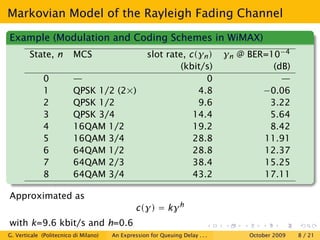
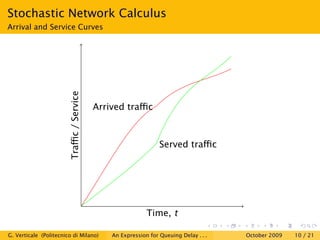
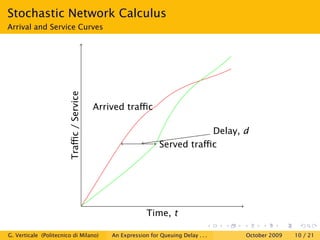
This document is a research paper that uses stochastic network calculus to model a wireless channel subject to Rayleigh fading and obtain an approximate closed-form expression for the probability tail of queuing delay. The paper presents the Markovian model of the Rayleigh fading channel, discusses the spectral gap in Markov chains and stochastic network calculus. It then derives the service envelope of the fading channel and compares the queuing delay expression to simulation results, finding a good match between the analysis and simulations. The conclusion is that stochastic network calculus can be used to successfully study wireless channels.








![Service Envelope of the Fading Channel
Mean and Variance of Service Curve in the Markovian Channel
Theorem
If the channel can be modeled as a reversible Markov Chain, then
λt + e−λt − 1
Var S(t) ≤ 2 Var[c]
λ2
We also provide a linear approximation:
t
Var S(t) ≤ 2 Var[c]
λ
The mean is trivial: E S(t) = E[c]t
G. Verticale (Politecnico di Milano) An Expression for Queuing Delay . . . October 2009 13 / 21](https://image.slidesharecdn.com/q2swinet-pres-091115132533-phpapp02/85/A-Closed-Form-Expression-for-Queuing-Delay-in-Rayleigh-Fading-Channels-Using-Stochastic-Network-Calculus-15-320.jpg)