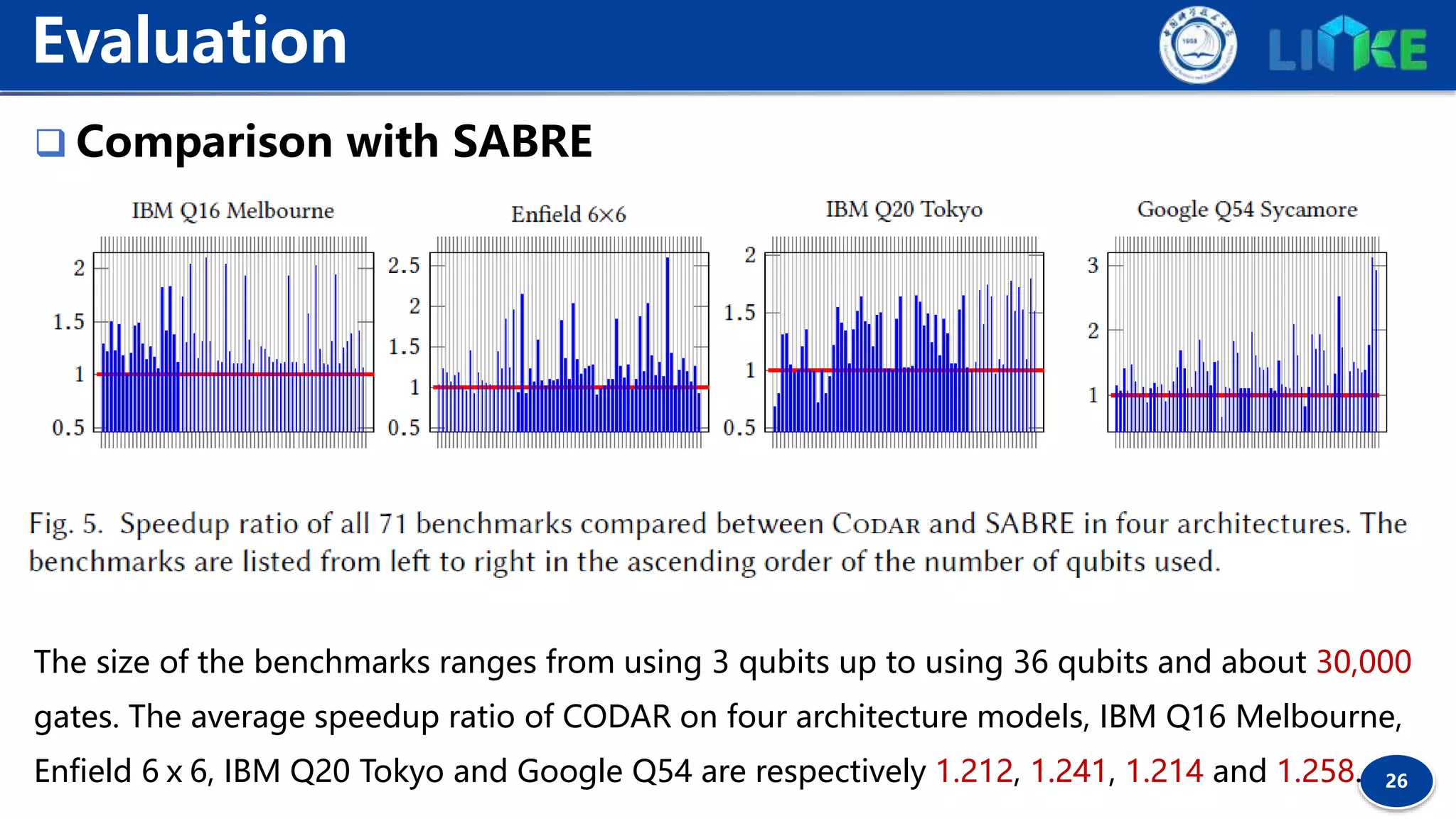
The document discusses a context-sensitive and duration-aware qubit mapping algorithm called Codar for various NISQ devices, aiming to optimize quantum circuits by addressing qubit connection limitations and gate duration differences. It presents a comparative evaluation of Codar's performance across several architectures, showing significant speedup ratios in executing quantum algorithms. Additionally, the document outlines ongoing research efforts focusing on noise effects and high-level algorithmic patterns.

1. 1
COntext-Sensitive and Duration-Aware
Qubit Mapping for Various NISQ Devices
Yu Zhang Hao-wei Deng Quan-xi Li
School of Computer Science & Technology
University of Science & Technology of China
PLanQC 2020, New Orleans, Jan. 19, 2020

2. 2
Quantum
Algorithms
QC: Multidisciplinary Intersection
Quantum
Algorithms
Quantum
Algorithms
Key Potential
Applications
Chemistry
Optimization
Machine
Learning
Material
Science
Unknown
Problems
gartner.com/smarterwithgartner
100-200 qubits
100s-1000s qubits
100s-1000s qubits
100s-1000s qubits
100, 000+ qubits
Algorithm
slgorithms
Quantum
Devices
Trapped Ion
Quantum
Information, UMD
Full software stack
for QC
Program at
higher-levels
of abstraction
Consider various
constraints of
quantum devices
Google’s Sycamore (54-Qubit)
Quantum Supremacy Using a
Programmable Superconducting Processor
Oct 23 2019 Nature
Sep 18, 2019
The opening of the
first IBM Quantum
Computation Center
in Poughkeepsie, NY
 Q53 Rochester
Intel’s 49-Qubit Chip
Tangle Lake
Jan 9 2018
May 5, 2018

3. 3
Most Existing QP Systems
Low-level quantum circuit
qreg q[3];
h q[0];
h q[1];
CX q[1], q[2];
CX q[0], q[2];
H q;
OpenQASM
Host language
+
Embedded DSL
High-level
Quantum
Compilation
ProjectQ
Low-level quantum circuit
Low-level
Quantum
Compilation
Hardware instructions (Pulse)

4. 4
Quantum Chips
 Superconducting  IonQ (Trapped ions)
IBM QX4 Tenerife
IBM Q20
IBM Q16 Melbourne
IonQ Q5
IonQ Q11
IBM Q53 Rochester
Google Q54 Sycamore
Quantum chips have various qubit coupling maps.

5. 5
Qubit Mapping Problem
CNOT
SWAP① CNOT②
Compiler need to insert SWAP into the quantum
circuit to fit the connection limitation in NISQ
hardware.
qreg q[3];
h q[0];
h q[1];
CX q[1], q[2];
CX q[0], q[2];
H q;
OpenQASM
NP-Complete
[CGO2018] Marcos Yukio Siraichi et al. Qubit Allocation.

6. 6
 Superconducting
X, Y, Z, H, S, T CNOT
Gate duration
 1-qubit: 80ns
 2-qubit: ~170ns
 Ion Trap
Ra
q , XX
Gate duration
 1-qubit: 20ms
 2-qubit: ~250ms
Various Quantum System Features

7. 7
How to insert SWAPs
 obtain feasible quantum circuits
for various NISQ devices

8. 8
 Formulate the qubit mapping problem into an equivalent
mathematical problem and apply a (SMT) Solver, e.g.
Unscalable, can only be applied to small-size cases
 Use heuristic search to obtain approximate results
Better in runtime especially when the circuit is in a large scale
Previous Solutions
 Ignore gate/operation duration difference
 Rarely consider the impact of program context on parallelism

9. 9
 Propose a Quantum Abstract Machine to abstract the
characteristics of different NISQ architectures
QAM here is distinct from that in the literature [arxiv1608.03355]， which
refers to an abstract machine architecture for classical/quantum
computations
 Propose a heuristic search algorithm CODAR considering
Gate duration difference
Program context
to explore more parallelism of the quantum program
Our Main Idea
[arxiv1608.03355] Robert S. Smith, Michael J. Curtis, William J. Zeng. A Practical Quantum Instruction
Set Architecture. Feb 2017.
CODAR: COntext-sensitive and Duration-Aware Remapping algorithm

10. 10
Which qubit pair is chosen to swap？
The earlier it can start, the better
Motivating Examples

11. 11
Which qubit pair is chosen to swap？
The earlier it can start, the better
 Impact of Program Context
Motivating Examples
cost 9 cycles
cost 8 cycles
Cycle

12. 12
Which qubit pair is chosen to swap？
The earlier it can start, the better
 Impact of Gate Duration Difference
Motivating Examples
cost 10 cycles
cost 9 cycles

13. 13
maQAM: Multi-architecture Adaptive
Quantum Abstract Machine

14. 14
Parameter info. of QC devices

15. 15
maQAM: Static +Dynamic Parts
Physical qubits，Elementary quantum operations
Qubit coupling map, Gate durations,
Distance between each qubit pair
Qubit map
Commutative front gate set
……

16. 16
Key Design on the CODAR Algorithm

17. 17
 Generate an executable gate sequence for a given input
OpenQASM program by
adjusting the gate sequence
inserting the swap operation
with the program semantics unchanged
Main Idea of CODAR
Fit quantum hardware limitation
Have better parallelism to reduce the weighted depth of the circuit

18. 18
Qubit Lock Mechanism
Each physical qubit has a Qubit Lock Tend.
A qubit's Tend is updated when a gate is
applied to this qubit.
By comparing each qubits' Tend with current time, CODAR is aware of which physical
qubits are occupied by previous gates and remap through free qubits. Different gates
with different duration will update Tend with different value. So CODAR is aware of the
gate duration difference.

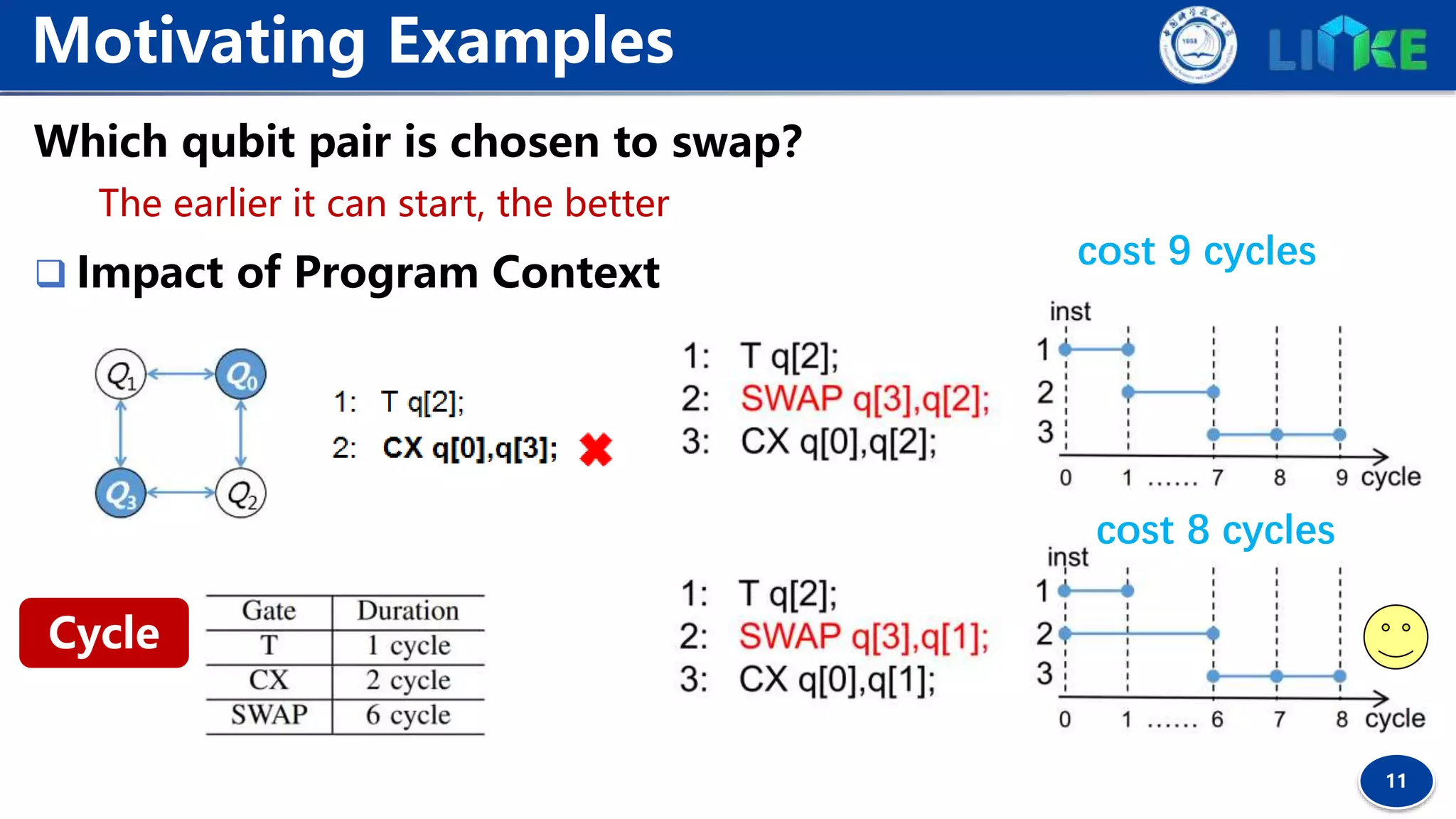
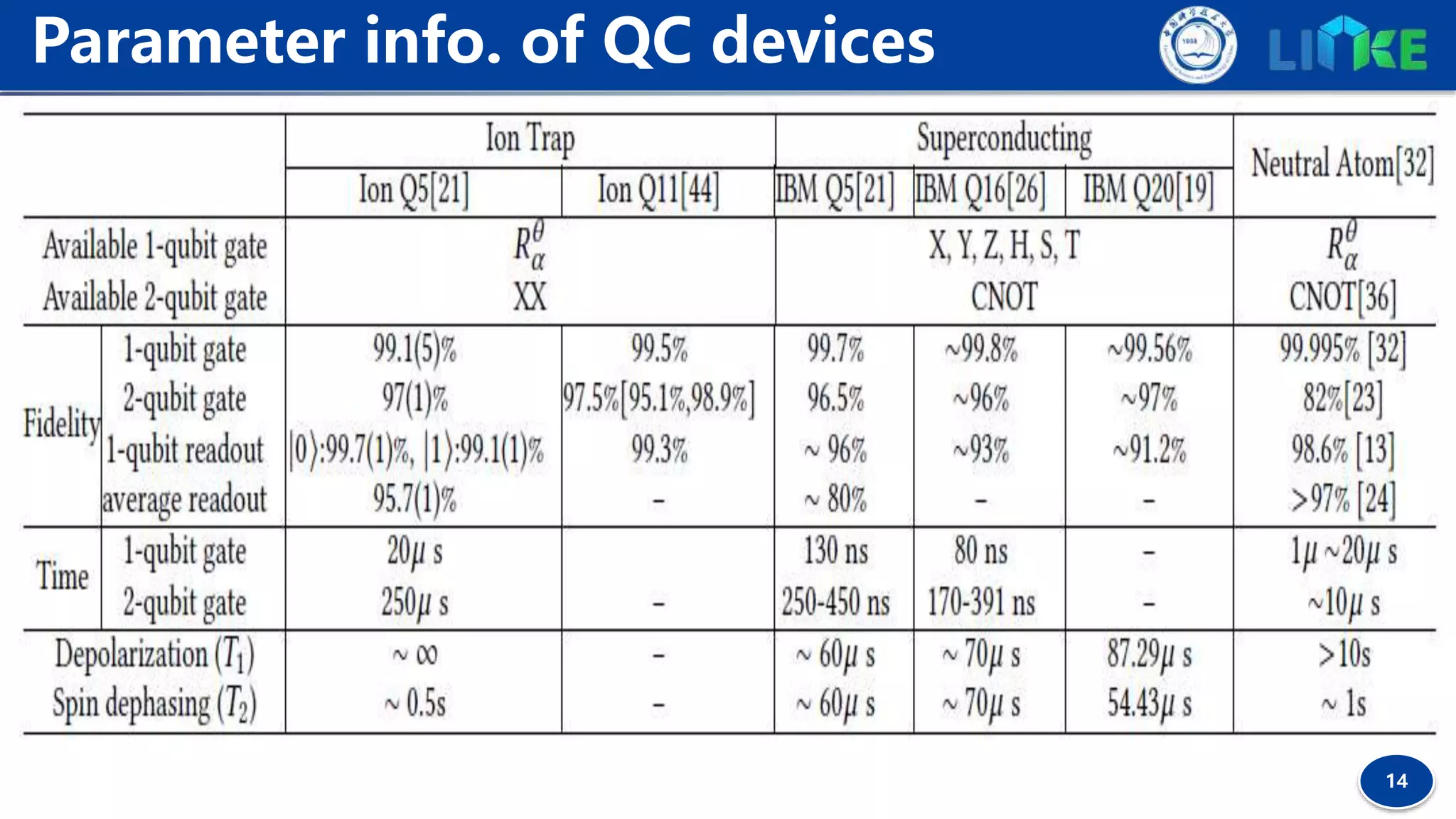
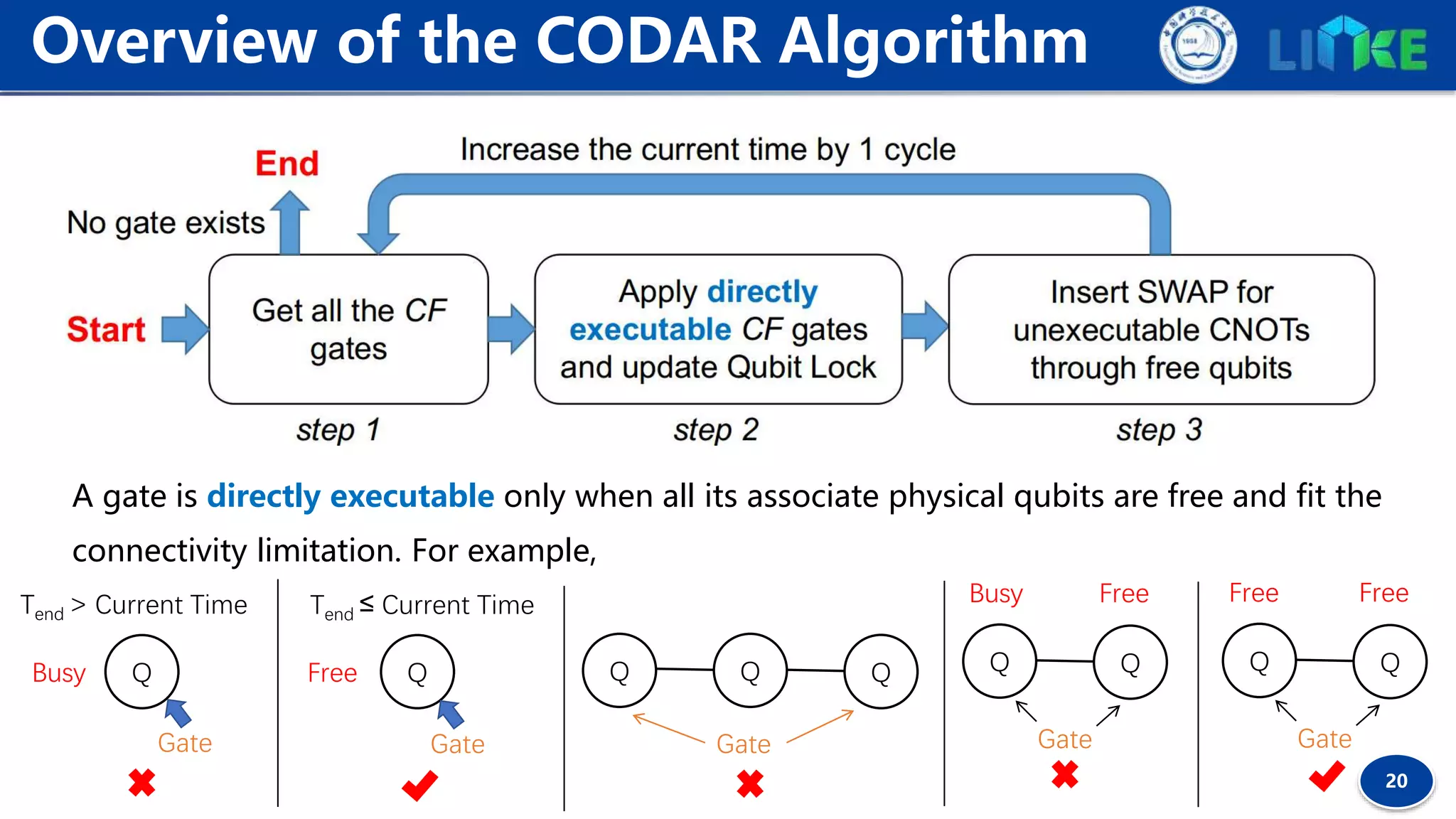
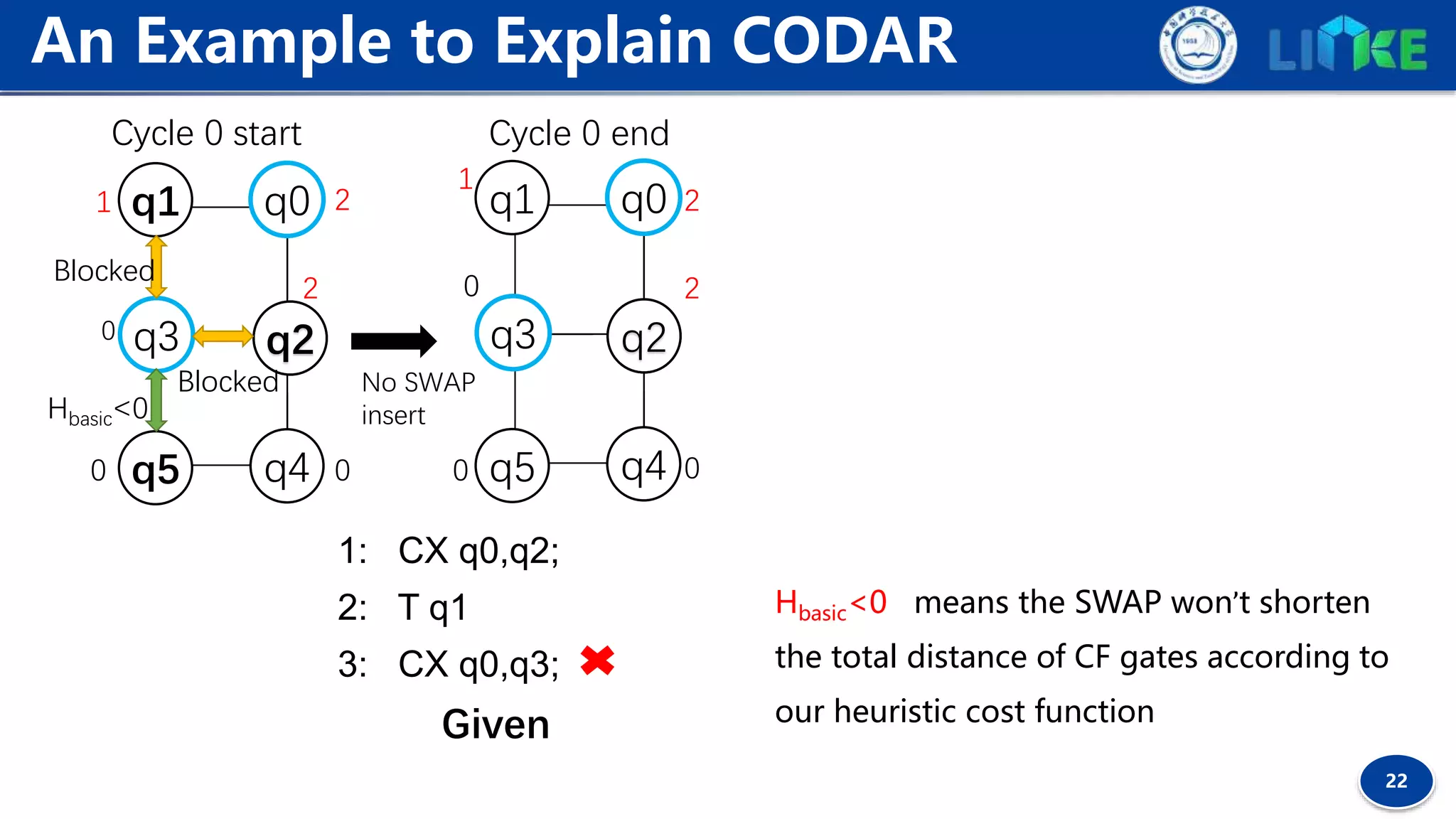
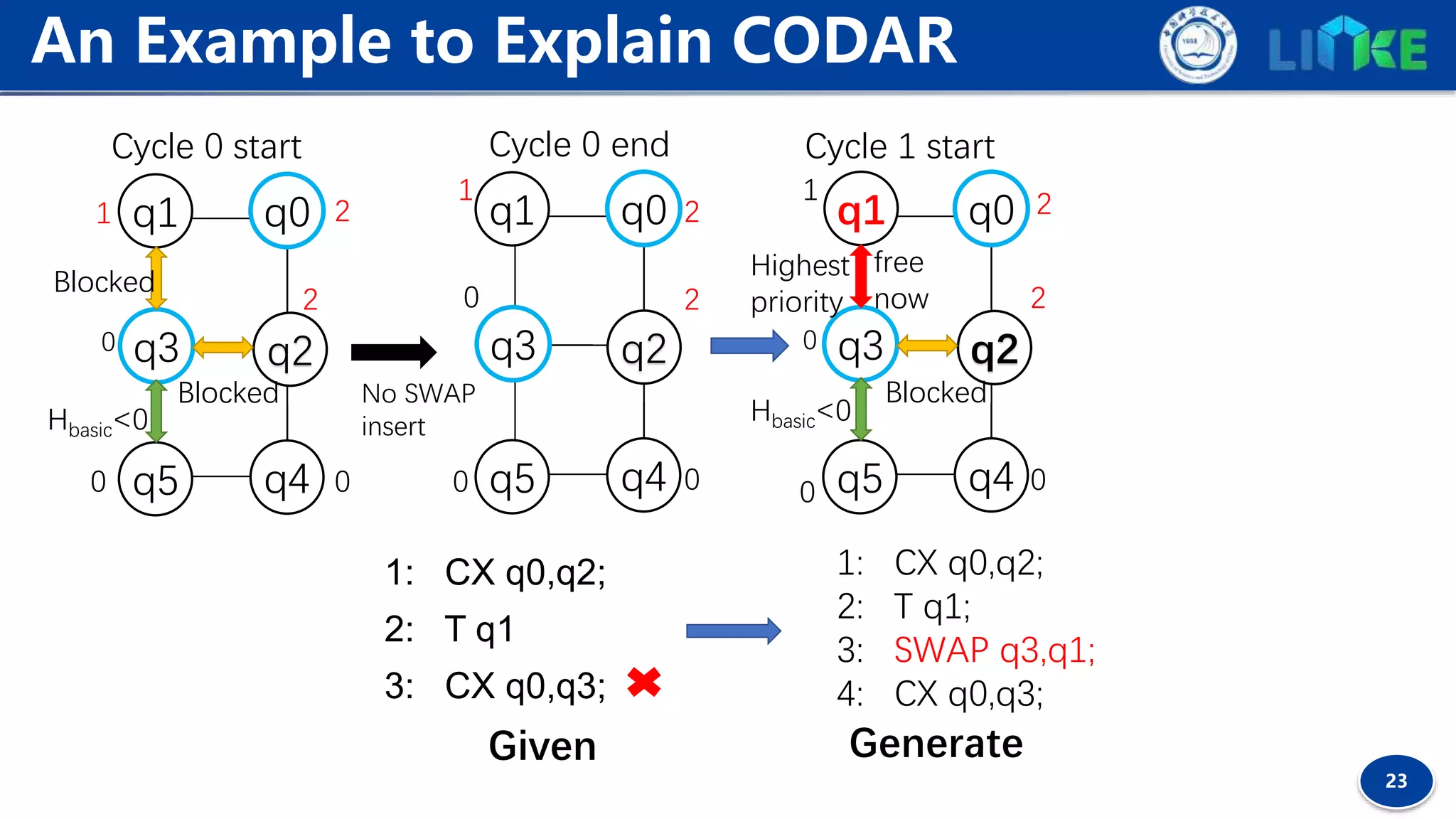
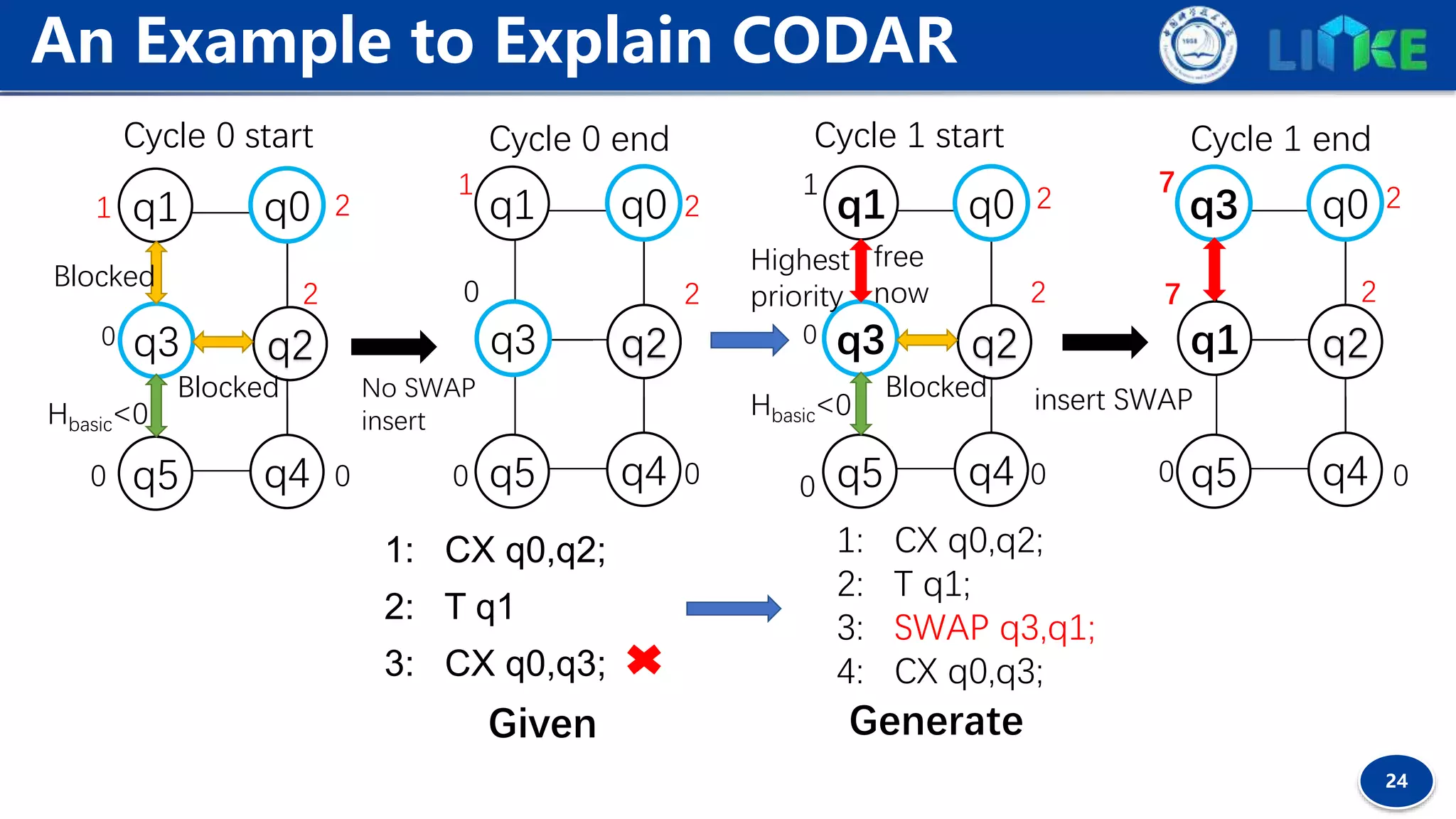
19. 19
 Commutativity between gates gA , gB can be resolved by
checking the relevant unitary operators ΑB=BA.
Commutativity Detection
Definition 1 (Commutative Forward Gate, CF gate). Given a gate sequence I=[g1 , g2 , ..., gk , ...],
∀gk ∈ I, gk is a commutative forward gate iff ∀j, 0 < j < k, gj and gk are commutative.
Choosing CF gates as logically-executable gates can expose more future contextual gates
for the heuristic search to determine better remapping solutions.

20. 20
Overview of the CODAR Algorithm
A gate is directly executable only when all its associate physical qubits are free and fit the
connectivity limitation. For example,
Q
Tend > Current Time
Busy QFree
Tend ≤ Current Time
Gate Gate
QQ Q
Gate
QQ
Gate
Busy Free
QQ
Gate
Free Free

21. 21
An Example to Explain CODAR
Hbasic<0
q5
q1
q2q3
q0
q4
0
0
0
00
0
Blocked
Blocked
Cycle 0
1: CX q0,q2;
2: T q1
3: CX q0,q3;
Given
Hbasic<0 means the SWAP won’t shorten
the total distance of CF gates according to
our heuristic cost function

22. 22
An Example to Explain CODAR
Hbasic<0 means the SWAP won’t shorten
the total distance of CF gates according to
our heuristic cost function
1: CX q0,q2;
2: T q1
3: CX q0,q3;
Given
q5
q1
q2q3
q0
q4
1
0 2
00
2
Hbasic<0
q5
q1
q2q3
q0
q4
1
0
2
00
2
No SWAP
insert
Blocked
Blocked
Cycle 0 endCycle 0 start

23. 23
An Example to Explain CODAR
1: CX q0,q2;
2: T q1
3: CX q0,q3;
1: CX q0,q2;
2: T q1;
3: SWAP q3,q1;
4: CX q0,q3;
Given Generate
q5
q1
q2q3
q0
q4
1
0 2
00
2
q5
q1
q3
q0
q4
1
0
2
00
2
Highest
priority
Hbasic<0
q5
q1
q2q3
q0
q4
1
0
2
00
2
No SWAP
insert
Blocked
Blocked
Hbasic<0
q2
Blocked
free
now
Cycle 0 end Cycle 1 startCycle 0 start

24. 24
An Example to Explain CODAR
q5
q1
q2q3
q0
q4
1
0 2
00
2
q5
q1
q3
q0
q4
1
0
2
00
2
Highest
priority
Hbasic<0
q5
q1
q2q3
q0
q4
1
0
2
00
2
No SWAP
insert
Blocked
Blocked
Hbasic<0
q2
Blocked
free
now
q5
q3
q2q1
q0
q4
7
7 2
0
2
insert SWAP
0
Cycle 0 end Cycle 1 startCycle 0 start Cycle 1 end
1: CX q0,q2;
2: T q1
3: CX q0,q3;
1: CX q0,q2;
2: T q1;
3: SWAP q3,q1;
4: CX q0,q3;
Given Generate

25. 25
Evaluation and Conclution

26. 26
 Comparison with SABRE
Evaluation
The size of the benchmarks ranges from using 3 qubits up to using 36 qubits and about 30,000
gates. The average speedup ratio of CODAR on four architecture models, IBM Q16 Melbourne,
Enfield 6ⅹ6, IBM Q20 Tokyo and Google Q54 are respectively 1.212, 1.241, 1.214 and 1.258.

27. 27
 Conclusion
The design of qubit lock and commutativity detection make CODAR aware
of program context and the gate duration difference, helping CODAR find
the remapping with good parallelism and reduce QC’s weighted depth
 Ongoing and Future Work
The impact of noise: noise of a gate cannot be accumulated sometimes
Are there any noise effect patterns？
The impact of sub-circuit patterns in high-level algorithms
Conclusion and Ongoing Work

28. 28
Yu Zhang (张昱)
yuzhang@ustc.edu.cn
CS@USTC
Thank you and any question?