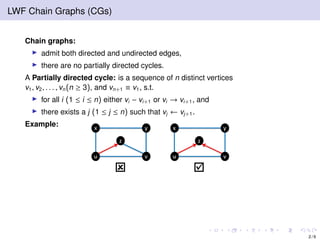
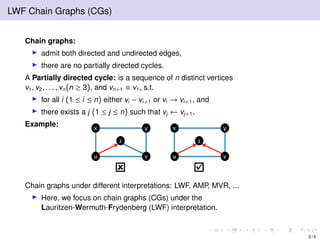
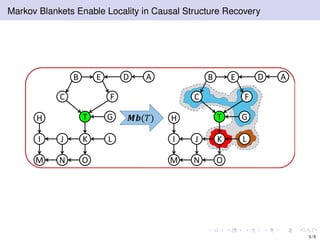
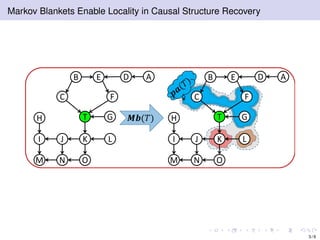
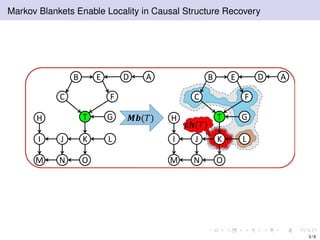
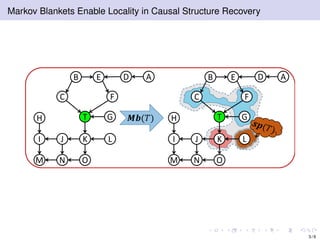
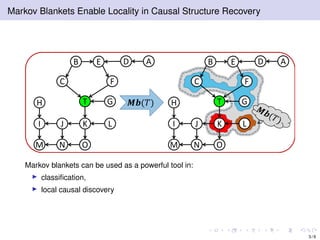
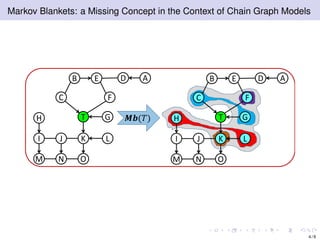
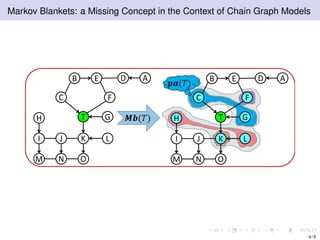
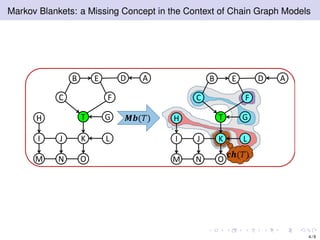
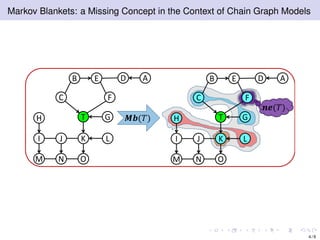
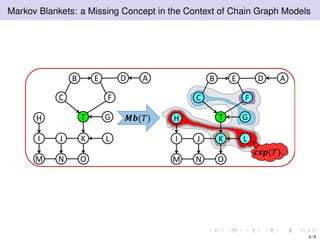
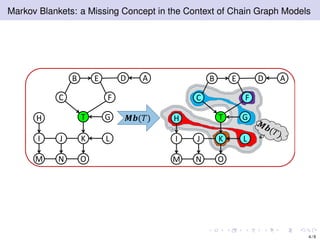
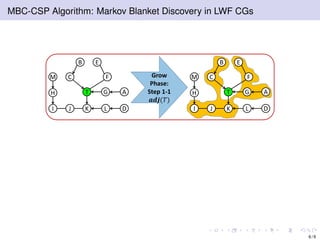
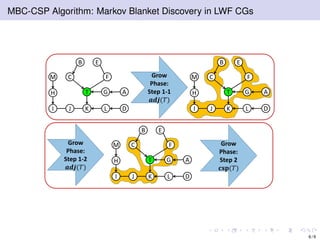
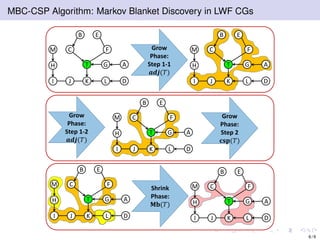
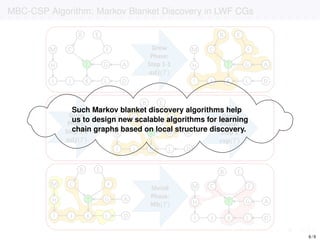
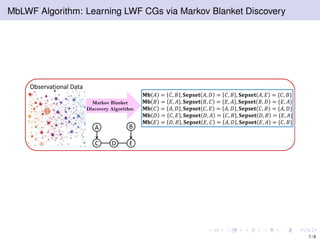
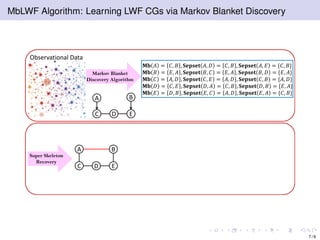
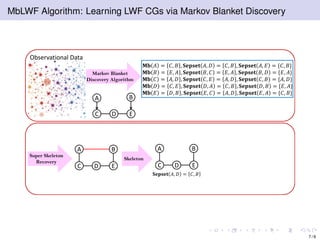
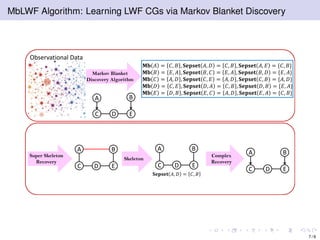
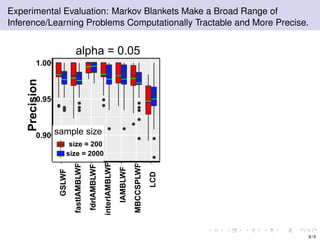
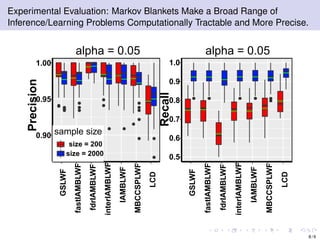
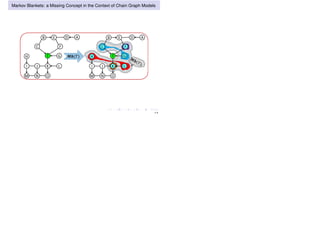
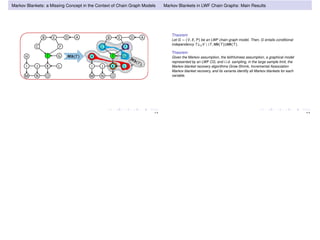
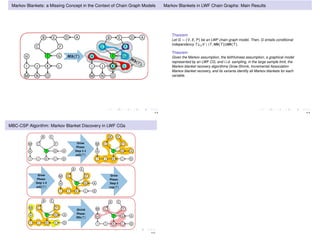
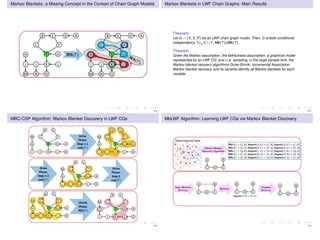
The document discusses learning LWF chain graphs through a Markov blanket discovery approach, emphasizing their capabilities in classifying and discovering local causal structures. It outlines the theoretical framework for Markov blankets, including conditional independencies and algorithmic frameworks for their recovery in LWF chain graphs. Additionally, it highlights the development of new algorithms for scalable Markov blanket discovery and their applications in improving inference and learning problems.

1. Learning LWF Chain Graphs:
A Markov Blanket Discovery Approach
Mohammad Ali Javidian
@ali javidian
Marco Valtorta
@MarcoGV2
Pooyan Jamshidi
@PooyanJamshidi
Department of Computer Science and Engineering
University of South Carolina
UAI 2020
1 / 9

2. LWF Chain Graphs (CGs)
Chain graphs:
admit both directed and undirected edges,
2 / 9

3. LWF Chain Graphs (CGs)
Chain graphs:
admit both directed and undirected edges,
there are no partially directed cycles.
2 / 9

4. LWF Chain Graphs (CGs)
Chain graphs:
admit both directed and undirected edges,
there are no partially directed cycles.
A Partially directed cycle: is a sequence of n distinct vertices
v1, v2, . . . , vn(n ≥ 3), and vn+1 ≡ v1, s.t.
for all i (1 ≤ i ≤ n) either vi − vi+1 or vi → vi+1, and
there exists a j (1 ≤ j ≤ n) such that vj ← vj+1.
2 / 9

5. LWF Chain Graphs (CGs)
Chain graphs:
admit both directed and undirected edges,
there are no partially directed cycles.
A Partially directed cycle: is a sequence of n distinct vertices
v1, v2, . . . , vn(n ≥ 3), and vn+1 ≡ v1, s.t.
for all i (1 ≤ i ≤ n) either vi − vi+1 or vi → vi+1, and
there exists a j (1 ≤ j ≤ n) such that vj ← vj+1.
Example:
2 / 9

6. LWF Chain Graphs (CGs)
Chain graphs:
admit both directed and undirected edges,
there are no partially directed cycles.
A Partially directed cycle: is a sequence of n distinct vertices
v1, v2, . . . , vn(n ≥ 3), and vn+1 ≡ v1, s.t.
for all i (1 ≤ i ≤ n) either vi − vi+1 or vi → vi+1, and
there exists a j (1 ≤ j ≤ n) such that vj ← vj+1.
Example:
Chain graphs under different interpretations: LWF, AMP, MVR, ...
Here, we focus on chain graphs (CGs) under the
Lauritzen-Wermuth-Frydenberg (LWF) interpretation.
2 / 9

7. Markov Blankets Enable Locality in Causal Structure Recovery
H
B
J
ADE
FC
I
OM N
K L
GT 𝑴𝒃(𝑇) H
B
J
ADE
FC
I
OM N
K L
GT
3 / 9

8. Markov Blankets Enable Locality in Causal Structure Recovery
H
B
J
ADE
FC
I
OM N
K L
GT 𝑴𝒃(𝑇) H
B
J
ADE
FC
I
OM N
K L
GT
3 / 9

9. Markov Blankets Enable Locality in Causal Structure Recovery
H
B
J
ADE
FC
I
OM N
K L
GT 𝑴𝒃(𝑇) H
B
J
ADE
FC
I
OM N
K L
GT
𝒄𝒉(𝑇)
3 / 9

10. Markov Blankets Enable Locality in Causal Structure Recovery
H
B
J
ADE
FC
I
OM N
K L
GT 𝑴𝒃(𝑇) H
B
J
ADE
FC
I
OM N
K L
GT
3 / 9

11. Markov Blankets Enable Locality in Causal Structure Recovery
H
B
J
ADE
FC
I
OM N
K L
GT 𝑴𝒃(𝑇) H
B
J
ADE
FC
I
OM N
K L
GT
Markov blankets can be used as a powerful tool in:
classification,
local causal discovery
3 / 9

12. Markov Blankets: a Missing Concept in the Context of Chain Graph Models
H
B
J
ADE
FC
I
OM N
K L
GT H
B
J
ADE
FC
I
OM N
K L
GT𝑴𝒃(𝑇)
4 / 9

13. Markov Blankets: a Missing Concept in the Context of Chain Graph Models
H
B
J
ADE
FC
I
OM N
K L
GT H
B
J
ADE
FC
I
OM N
K L
GT𝑴𝒃(𝑇)
𝒑𝒂(𝑇)
4 / 9

14. Markov Blankets: a Missing Concept in the Context of Chain Graph Models
H
B
J
ADE
FC
I
OM N
K L
GT H
B
J
ADE
FC
I
OM N
K L
GT𝑴𝒃(𝑇)
𝒄𝒉(𝑇)
4 / 9

15. Markov Blankets: a Missing Concept in the Context of Chain Graph Models
H
B
J
ADE
FC
I
OM N
K L
GT H
B
J
ADE
FC
I
OM N
K L
GT𝑴𝒃(𝑇)
𝒏𝒆(𝑇)
4 / 9

16. Markov Blankets: a Missing Concept in the Context of Chain Graph Models
H
B
J
ADE
FC
I
OM N
K L
GT H
B
J
ADE
FC
I
OM N
K L
GT𝑴𝒃(𝑇)
𝒄𝒔𝒑(𝑇)
4 / 9

17. Markov Blankets: a Missing Concept in the Context of Chain Graph Models
H
B
J
ADE
FC
I
OM N
K L
GT H
B
J
ADE
FC
I
OM N
K L
GT𝑴𝒃(𝑇)
4 / 9

18. Markov Blankets in LWF Chain Graphs: Main Results
Theorem (Characterization of Markov Blankets in LWF CGs)
Let G = (V, E, P) be an LWF chain graph model. Then, G entails conditional
independency T⊥⊥pV {T, Mb(T)}|Mb(T), i.e., the Markov blanket of the target
variable T in an LWF CG probabilistically shields T from the rest of the variables.
5 / 9

19. Markov Blankets in LWF Chain Graphs: Main Results
Theorem (Characterization of Markov Blankets in LWF CGs)
Let G = (V, E, P) be an LWF chain graph model. Then, G entails conditional
independency T⊥⊥pV {T, Mb(T)}|Mb(T), i.e., the Markov blanket of the target
variable T in an LWF CG probabilistically shields T from the rest of the variables.
Theorem (Standard algorithms for Markov blanket recovery in LWF CGs)
Given the Markov assumption, the faithfulness assumption, a graphical model
represented by an LWF CG, and i.i.d. sampling, in the large sample limit, the
Markov blanket recovery algorithms Grow-Shrink, Incremental Association
Markov blanket recovery, and its variants identify all Markov blankets for each
variable.
5 / 9

20. Markov Blankets in LWF Chain Graphs: Main Results
Theorem (Characterization of Markov Blankets in LWF CGs)
Let G = (V, E, P) be an LWF chain graph model. Then, G entails conditional
independency T⊥⊥pV {T, Mb(T)}|Mb(T), i.e., the Markov blanket of the target
variable T in an LWF CG probabilistically shields T from the rest of the variables.
Theorem (Standard algorithms for Markov blanket recovery in LWF CGs)
Given the Markov assumption, the faithfulness assumption, a graphical model
represented by an LWF CG, and i.i.d. sampling, in the large sample limit, the
Markov blanket recovery algorithms Grow-Shrink, Incremental Association
Markov blanket recovery, and its variants identify all Markov blankets for each
variable.
The characterization of Markov blankets in chain graphs
enables us to develop new algorithms that are specifically
designed for learning Markov blankets in chain graphs.
5 / 9

21. MBC-CSP Algorithm: Markov Blanket Discovery in LWF CGs
H
B
J
A
E
FC
I
M
K L
GT
D
Grow
Phase:
Step 1-1
𝒂𝒅𝒋(𝑇)
H
B
J
A
E
FC
I
M
K L
GT
D
Grow
Phase:
Step 1-2
𝒂𝒅𝒋(𝑇)
H
B
J
A
E
FC
I
M
K L
GT
D
Grow
Phase:
Step 2
𝐜𝐬𝐩(𝑇)
6 / 9

22. MBC-CSP Algorithm: Markov Blanket Discovery in LWF CGs
H
B
J
A
E
FC
I
M
K L
GT
D
Grow
Phase:
Step 1-1
𝒂𝒅𝒋(𝑇)
H
B
J
A
E
FC
I
M
K L
GT
D
Grow
Phase:
Step 1-2
𝒂𝒅𝒋(𝑇)
H
B
J
A
E
FC
I
M
K L
GT
D
Grow
Phase:
Step 2
𝐜𝐬𝐩(𝑇)
H
B
J
A
E
FC
I
M
K L
GT
D
Grow
Phase:
Step 1-1
𝒂𝒅𝒋(𝑇)
H
B
J
A
E
FC
I
M
K L
GT
D
Grow
Phase:
Step 1-2
𝒂𝒅𝒋(𝑇)
H
B
J
A
E
FC
I
M
K L
GT
D
Grow
Phase:
Step 2
𝐜𝐬𝐩(𝑇)
6 / 9

23. MBC-CSP Algorithm: Markov Blanket Discovery in LWF CGs
H
B
J
A
E
FC
I
M
K L
GT
D
Grow
Phase:
Step 1-1
𝒂𝒅𝒋(𝑇)
H
B
J
A
E
FC
I
M
K L
GT
D
Grow
Phase:
Step 1-2
𝒂𝒅𝒋(𝑇)
H
B
J
A
E
FC
I
M
K L
GT
D
Grow
Phase:
Step 2
𝐜𝐬𝐩(𝑇)
H
B
J
A
E
FC
I
M
K L
GT
D
Grow
Phase:
Step 1-1
𝒂𝒅𝒋(𝑇)
H
B
J
A
E
FC
I
M
K L
GT
D
Grow
Phase:
Step 1-2
𝒂𝒅𝒋(𝑇)
H
B
J
A
E
FC
I
M
K L
GT
D
Grow
Phase:
Step 2
𝐜𝐬𝐩(𝑇)
Shrink
Phase:
𝐌𝐛(𝑇) H
B
J
A
E
FC
I
M
K L
GT
D
H
B
J
A
E
FC
I
M
K L
GT
D
6 / 9

24. MBC-CSP Algorithm: Markov Blanket Discovery in LWF CGs
H
B
J
A
E
FC
I
M
K L
GT
D
Grow
Phase:
Step 1-1
𝒂𝒅𝒋(𝑇)
H
B
J
A
E
FC
I
M
K L
GT
D
Grow
Phase:
Step 1-2
𝒂𝒅𝒋(𝑇)
H
B
J
A
E
FC
I
M
K L
GT
D
Grow
Phase:
Step 2
𝐜𝐬𝐩(𝑇)
H
B
J
A
E
FC
I
M
K L
GT
D
Grow
Phase:
Step 1-1
𝒂𝒅𝒋(𝑇)
H
B
J
A
E
FC
I
M
K L
GT
D
Grow
Phase:
Step 1-2
𝒂𝒅𝒋(𝑇)
H
B
J
A
E
FC
I
M
K L
GT
D
Grow
Phase:
Step 2
𝐜𝐬𝐩(𝑇)
Shrink
Phase:
𝐌𝐛(𝑇) H
B
J
A
E
FC
I
M
K L
GT
D
H
B
J
A
E
FC
I
M
K L
GT
D
Such Markov blanket discovery algorithms help
us to design new scalable algorithms for learning
chain graphs based on local structure discovery.
6 / 9

25. MbLWF Algorithm: Learning LWF CGs via Markov Blanket Discovery
Observational Data
Markov Blanket
Discovery Algorithm
A
DC E
B
𝐌𝐛 𝐴 = 𝐶, 𝐵 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐴, 𝐷 = 𝐶, 𝐵 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐴, 𝐸 = {𝐶, 𝐵}
𝐌𝐛 𝐵 = 𝐸, 𝐴 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐵, 𝐶 = 𝐸, 𝐴 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐵, 𝐷 = {𝐸, 𝐴}
𝐌𝐛 𝐶 = 𝐴, 𝐷 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐶, 𝐸 = 𝐴, 𝐷 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐶, 𝐵 = {𝐴, 𝐷}
𝐌𝐛 𝐷 = 𝐶, 𝐸 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐷, 𝐴 = 𝐶, 𝐵 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐷, 𝐵 = {𝐸, 𝐴}
𝐌𝐛 𝐸 = 𝐷, 𝐵 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐸, 𝐶 = 𝐴, 𝐷 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐸, 𝐴 = {𝐶, 𝐵}
7 / 9

26. MbLWF Algorithm: Learning LWF CGs via Markov Blanket Discovery
Observational Data
Markov Blanket
Discovery Algorithm
A
DC E
B
𝐌𝐛 𝐴 = 𝐶, 𝐵 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐴, 𝐷 = 𝐶, 𝐵 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐴, 𝐸 = {𝐶, 𝐵}
𝐌𝐛 𝐵 = 𝐸, 𝐴 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐵, 𝐶 = 𝐸, 𝐴 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐵, 𝐷 = {𝐸, 𝐴}
𝐌𝐛 𝐶 = 𝐴, 𝐷 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐶, 𝐸 = 𝐴, 𝐷 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐶, 𝐵 = {𝐴, 𝐷}
𝐌𝐛 𝐷 = 𝐶, 𝐸 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐷, 𝐴 = 𝐶, 𝐵 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐷, 𝐵 = {𝐸, 𝐴}
𝐌𝐛 𝐸 = 𝐷, 𝐵 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐸, 𝐶 = 𝐴, 𝐷 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐸, 𝐴 = {𝐶, 𝐵}
A
DC E
B
Super Skeleton
Recovery
7 / 9

27. MbLWF Algorithm: Learning LWF CGs via Markov Blanket Discovery
Observational Data
Markov Blanket
Discovery Algorithm
A
DC E
B
𝐌𝐛 𝐴 = 𝐶, 𝐵 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐴, 𝐷 = 𝐶, 𝐵 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐴, 𝐸 = {𝐶, 𝐵}
𝐌𝐛 𝐵 = 𝐸, 𝐴 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐵, 𝐶 = 𝐸, 𝐴 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐵, 𝐷 = {𝐸, 𝐴}
𝐌𝐛 𝐶 = 𝐴, 𝐷 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐶, 𝐸 = 𝐴, 𝐷 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐶, 𝐵 = {𝐴, 𝐷}
𝐌𝐛 𝐷 = 𝐶, 𝐸 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐷, 𝐴 = 𝐶, 𝐵 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐷, 𝐵 = {𝐸, 𝐴}
𝐌𝐛 𝐸 = 𝐷, 𝐵 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐸, 𝐶 = 𝐴, 𝐷 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐸, 𝐴 = {𝐶, 𝐵}
A
DC E
B
Super Skeleton
Recovery
𝐒𝐞𝐩𝐬𝐞𝐭 𝐴, 𝐷 = 𝐶, 𝐵
Skeleton
A
DC E
B
7 / 9

28. MbLWF Algorithm: Learning LWF CGs via Markov Blanket Discovery
Observational Data
Markov Blanket
Discovery Algorithm
A
DC E
B
𝐌𝐛 𝐴 = 𝐶, 𝐵 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐴, 𝐷 = 𝐶, 𝐵 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐴, 𝐸 = {𝐶, 𝐵}
𝐌𝐛 𝐵 = 𝐸, 𝐴 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐵, 𝐶 = 𝐸, 𝐴 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐵, 𝐷 = {𝐸, 𝐴}
𝐌𝐛 𝐶 = 𝐴, 𝐷 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐶, 𝐸 = 𝐴, 𝐷 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐶, 𝐵 = {𝐴, 𝐷}
𝐌𝐛 𝐷 = 𝐶, 𝐸 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐷, 𝐴 = 𝐶, 𝐵 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐷, 𝐵 = {𝐸, 𝐴}
𝐌𝐛 𝐸 = 𝐷, 𝐵 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐸, 𝐶 = 𝐴, 𝐷 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐸, 𝐴 = {𝐶, 𝐵}
A
DC E
B
Super Skeleton
Recovery
𝐒𝐞𝐩𝐬𝐞𝐭 𝐴, 𝐷 = 𝐶, 𝐵
Skeleton
A
DC E
B
A
DC E
BComplex
Recovery
7 / 9

29. Experimental Evaluation: Markov Blankets Make a Broad Range of
Inference/Learning Problems Computationally Tractable and More Precise.
●●
●●
●
●
●
●
●
●
●
●
● ●
●
●
●
●
●
●
●
●0.90
0.95
1.00 GSLWF
fastIAMBLWF
fdrIAMBLWF
interIAMBLWF
IAMBLWF
MBCCSPLWF
LCD
Precision
sample size
size = 200
size = 2000
alpha = 0.05
8 / 9

30. Experimental Evaluation: Markov Blankets Make a Broad Range of
Inference/Learning Problems Computationally Tractable and More Precise.
●●
●●
●
●
●
●
●
●
●
●
● ●
●
●
●
●
●
●
●
●0.90
0.95
1.00 GSLWF
fastIAMBLWF
fdrIAMBLWF
interIAMBLWF
IAMBLWF
MBCCSPLWF
LCD
Precision
sample size
size = 200
size = 2000
alpha = 0.05
● ● ● ●
●
●
0.5
0.6
0.7
0.8
0.9
1.0
GSLWF
fastIAMBLWF
fdrIAMBLWF
interIAMBLWF
IAMBLWF
MBCCSPLWF
LCD
Recall
alpha = 0.05
8 / 9

31. Markov Blankets: a Missing Concept in the Context of Chain Graph Models
H
B
J
ADE
FC
I
OM N
K L
GT H
B
J
ADE
FC
I
OM N
K L
GT𝑴𝒃(𝑇)
4 / 9

32. Markov Blankets: a Missing Concept in the Context of Chain Graph Models
H
B
J
ADE
FC
I
OM N
K L
GT H
B
J
ADE
FC
I
OM N
K L
GT𝑴𝒃(𝑇)
4 / 9
Markov Blankets in LWF Chain Graphs: Main Results
Theorem
Let G = (V, E, P) be an LWF chain graph model. Then, G entails conditional
independency T⊥⊥pV {T, Mb(T)}|Mb(T).
Theorem
Given the Markov assumption, the faithfulness assumption, a graphical model
represented by an LWF CG, and i.i.d. sampling, in the large sample limit, the
Markov blanket recovery algorithms Grow-Shrink, Incremental Association
Markov blanket recovery, and its variants identify all Markov blankets for each
variable.
5 / 9

33. Markov Blankets: a Missing Concept in the Context of Chain Graph Models
H
B
J
ADE
FC
I
OM N
K L
GT H
B
J
ADE
FC
I
OM N
K L
GT𝑴𝒃(𝑇)
4 / 9
Markov Blankets in LWF Chain Graphs: Main Results
Theorem
Let G = (V, E, P) be an LWF chain graph model. Then, G entails conditional
independency T⊥⊥pV {T, Mb(T)}|Mb(T).
Theorem
Given the Markov assumption, the faithfulness assumption, a graphical model
represented by an LWF CG, and i.i.d. sampling, in the large sample limit, the
Markov blanket recovery algorithms Grow-Shrink, Incremental Association
Markov blanket recovery, and its variants identify all Markov blankets for each
variable.
5 / 9
MBC-CSP Algorithm: Markov Blanket Discovery in LWF CGs
H
B
J
A
E
FC
I
M
K L
GT
D
Grow
Phase:
Step 1-1
𝒂𝒅𝒋(𝑇)
H
B
J
A
E
FC
I
M
K L
GT
D
Grow
Phase:
Step 1-2
𝒂𝒅𝒋(𝑇)
H
B
J
A
E
FC
I
M
K L
GT
D
Grow
Phase:
Step 2
𝐜𝐬𝐩(𝑇)
H
B
J
A
E
FC
I
M
K L
GT
D
Grow
Phase:
Step 1-1
𝒂𝒅𝒋(𝑇)
H
B
J
A
E
FC
I
M
K L
GT
D
Grow
Phase:
Step 1-2
𝒂𝒅𝒋(𝑇)
H
B
J
A
E
FC
I
M
K L
GT
D
Grow
Phase:
Step 2
𝐜𝐬𝐩(𝑇)
Shrink
Phase:
𝐌𝐛(𝑇) H
B
J
A
E
FC
I
M
K L
GT
D
H
B
J
A
E
FC
I
M
K L
GT
D
6 / 9

34. Markov Blankets: a Missing Concept in the Context of Chain Graph Models
H
B
J
ADE
FC
I
OM N
K L
GT H
B
J
ADE
FC
I
OM N
K L
GT𝑴𝒃(𝑇)
4 / 9
Markov Blankets in LWF Chain Graphs: Main Results
Theorem
Let G = (V, E, P) be an LWF chain graph model. Then, G entails conditional
independency T⊥⊥pV {T, Mb(T)}|Mb(T).
Theorem
Given the Markov assumption, the faithfulness assumption, a graphical model
represented by an LWF CG, and i.i.d. sampling, in the large sample limit, the
Markov blanket recovery algorithms Grow-Shrink, Incremental Association
Markov blanket recovery, and its variants identify all Markov blankets for each
variable.
5 / 9
MBC-CSP Algorithm: Markov Blanket Discovery in LWF CGs
H
B
J
A
E
FC
I
M
K L
GT
D
Grow
Phase:
Step 1-1
𝒂𝒅𝒋(𝑇)
H
B
J
A
E
FC
I
M
K L
GT
D
Grow
Phase:
Step 1-2
𝒂𝒅𝒋(𝑇)
H
B
J
A
E
FC
I
M
K L
GT
D
Grow
Phase:
Step 2
𝐜𝐬𝐩(𝑇)
H
B
J
A
E
FC
I
M
K L
GT
D
Grow
Phase:
Step 1-1
𝒂𝒅𝒋(𝑇)
H
B
J
A
E
FC
I
M
K L
GT
D
Grow
Phase:
Step 1-2
𝒂𝒅𝒋(𝑇)
H
B
J
A
E
FC
I
M
K L
GT
D
Grow
Phase:
Step 2
𝐜𝐬𝐩(𝑇)
Shrink
Phase:
𝐌𝐛(𝑇) H
B
J
A
E
FC
I
M
K L
GT
D
H
B
J
A
E
FC
I
M
K L
GT
D
6 / 9
MbLWF Algorithm: Learning LWF CGs via Markov Blanket Discovery
Observational Data
Markov Blanket
Discovery Algorithm
A
DC E
B
𝐌𝐛 𝐴 = 𝐶, 𝐵 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐴, 𝐷 = 𝐶, 𝐵 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐴, 𝐸 = {𝐶, 𝐵}
𝐌𝐛 𝐵 = 𝐸, 𝐴 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐵, 𝐶 = 𝐸, 𝐴 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐵, 𝐷 = {𝐸, 𝐴}
𝐌𝐛 𝐶 = 𝐴, 𝐷 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐶, 𝐸 = 𝐴, 𝐷 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐶, 𝐵 = {𝐴, 𝐷}
𝐌𝐛 𝐷 = 𝐶, 𝐸 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐷, 𝐴 = 𝐶, 𝐵 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐷, 𝐵 = {𝐸, 𝐴}
𝐌𝐛 𝐸 = 𝐷, 𝐵 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐸, 𝐶 = 𝐴, 𝐷 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐸, 𝐴 = {𝐶, 𝐵}
A
DC E
B
Super Skeleton
Recovery
𝐒𝐞𝐩𝐬𝐞𝐭 𝐴, 𝐷 = 𝐶, 𝐵
Skeleton
A
DC E
B
A
DC E
BComplex
Recovery
7 / 9

35. Markov Blankets: a Missing Concept in the Context of Chain Graph Models
H
B
J
ADE
FC
I
OM N
K L
GT H
B
J
ADE
FC
I
OM N
K L
GT𝑴𝒃(𝑇)
4 / 9
Markov Blankets in LWF Chain Graphs: Main Results
Theorem
Let G = (V, E, P) be an LWF chain graph model. Then, G entails conditional
independency T⊥⊥pV {T, Mb(T)}|Mb(T).
Theorem
Given the Markov assumption, the faithfulness assumption, a graphical model
represented by an LWF CG, and i.i.d. sampling, in the large sample limit, the
Markov blanket recovery algorithms Grow-Shrink, Incremental Association
Markov blanket recovery, and its variants identify all Markov blankets for each
variable.
5 / 9
MBC-CSP Algorithm: Markov Blanket Discovery in LWF CGs
H
B
J
A
E
FC
I
M
K L
GT
D
Grow
Phase:
Step 1-1
𝒂𝒅𝒋(𝑇)
H
B
J
A
E
FC
I
M
K L
GT
D
Grow
Phase:
Step 1-2
𝒂𝒅𝒋(𝑇)
H
B
J
A
E
FC
I
M
K L
GT
D
Grow
Phase:
Step 2
𝐜𝐬𝐩(𝑇)
H
B
J
A
E
FC
I
M
K L
GT
D
Grow
Phase:
Step 1-1
𝒂𝒅𝒋(𝑇)
H
B
J
A
E
FC
I
M
K L
GT
D
Grow
Phase:
Step 1-2
𝒂𝒅𝒋(𝑇)
H
B
J
A
E
FC
I
M
K L
GT
D
Grow
Phase:
Step 2
𝐜𝐬𝐩(𝑇)
Shrink
Phase:
𝐌𝐛(𝑇) H
B
J
A
E
FC
I
M
K L
GT
D
H
B
J
A
E
FC
I
M
K L
GT
D
6 / 9
MbLWF Algorithm: Learning LWF CGs via Markov Blanket Discovery
Observational Data
Markov Blanket
Discovery Algorithm
A
DC E
B
𝐌𝐛 𝐴 = 𝐶, 𝐵 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐴, 𝐷 = 𝐶, 𝐵 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐴, 𝐸 = {𝐶, 𝐵}
𝐌𝐛 𝐵 = 𝐸, 𝐴 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐵, 𝐶 = 𝐸, 𝐴 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐵, 𝐷 = {𝐸, 𝐴}
𝐌𝐛 𝐶 = 𝐴, 𝐷 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐶, 𝐸 = 𝐴, 𝐷 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐶, 𝐵 = {𝐴, 𝐷}
𝐌𝐛 𝐷 = 𝐶, 𝐸 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐷, 𝐴 = 𝐶, 𝐵 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐷, 𝐵 = {𝐸, 𝐴}
𝐌𝐛 𝐸 = 𝐷, 𝐵 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐸, 𝐶 = 𝐴, 𝐷 , 𝐒𝐞𝐩𝐬𝐞𝐭 𝐸, 𝐴 = {𝐶, 𝐵}
A
DC E
B
Super Skeleton
Recovery
𝐒𝐞𝐩𝐬𝐞𝐭 𝐴, 𝐷 = 𝐶, 𝐵
Skeleton
A
DC E
B
A
DC E
BComplex
Recovery
7 / 9
All code, data, and supplementary materials are available at:
https://majavid.github.io/structurelearning/blog/2020/uai/