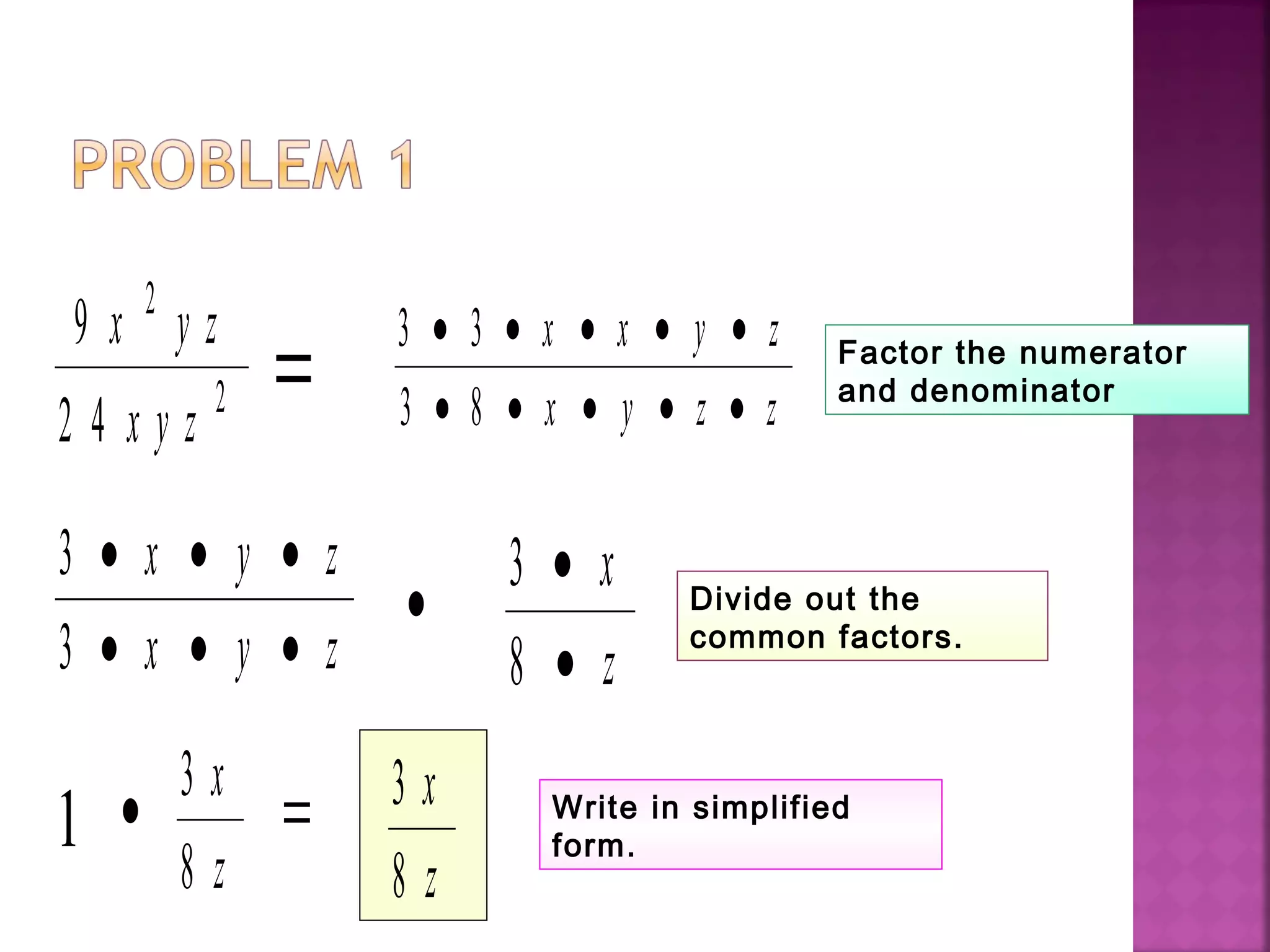
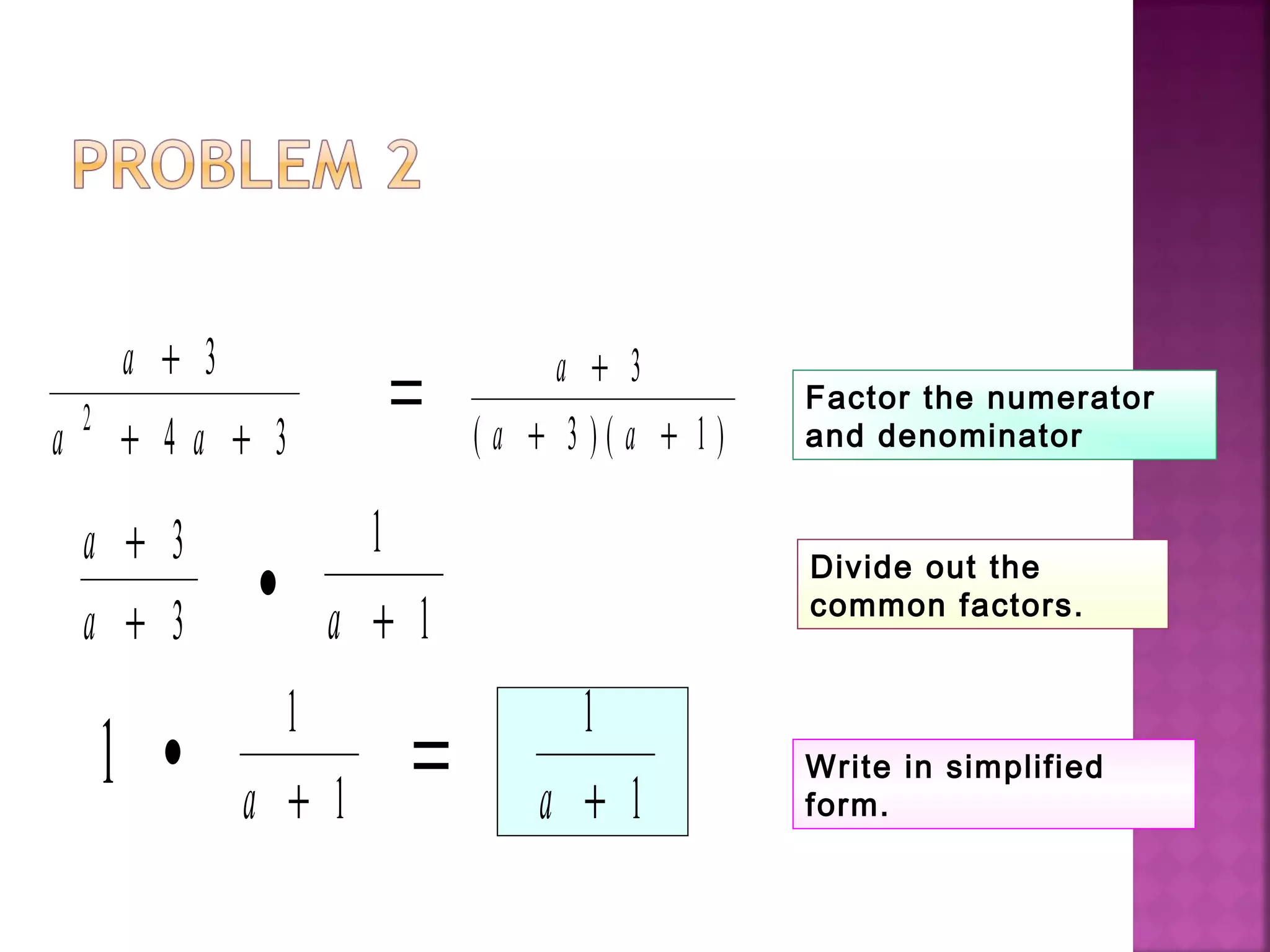
This document provides instructions for simplifying rational expressions by factoring the numerator and denominator and dividing out common factors. It includes examples of simplifying various rational expressions step-by-step. The objective is to be able to put rational expressions into their simplest form by factoring and cancelling out common terms between the numerator and denominator.

1. Simplifying Basic
Rational Expressions
Prepared by:
Sandra
Sanvictores
Leslie Limjuco
Duane

2.  The objective is to be able to simplify a
rational expression
 Another objective is to know how to factor
the numerator and denominator and to,
 Divide out the common factors

3.  Polynomial – an expression of more than two
algebraic terms, especially the sum of several terms
that contain different powers of the same
variable(s).
 Rational expression - a fraction in which the
numerator and/or the denominator are polynomials.
 Domain of a rational expression – the set of all
possible values of the variables.
 Reduced form – a rational expression in which the
numerator and denominator have no factors in
common.

4.  Divide out the
common factors
 Factor the
numerator and
denominator and
then divide the
common factors

5. Step 1 – Identify any factors which are common to both the
numerator and the denominator.
5
5 7
x
x( )−
The numerator and denominator
have a common factor.
The common factor is the five.

6. Step 2 – Divide out the common factors.
The fives can be divided since 5/5 = 1
The x remains in the numerator.
The (x-7) remains in the denominator
5
5 7
x
x( )−
=
x
x − 7

7. Factor the numerator.
Factor the denominator.
Divide out the common factors.
Write in simplified form.
3 9
1 2
2
3
x x
x
+

8. Step 1: Look for common factors
to both terms in the numerator.
3 9
1 2
2
3
x x
x
+ ♦3 is a factor of both 3 and 9.
♦X is a factor of both x2
and x.
Step 2: Factor the numerator.
3 9
1 2
2
3
x x
x
+ 3 3
12 3
x x
x
( )+

9. Step 3: Look for common factors to the
terms in the denominator and factor.
3 9
1 2
2
3
x x
x
+
The denominator only has one term.
The 12 and x3
can be factored.
The 12 can be factored into 3 x 4.
The x3
can be written as x • x2
.
3 9
1 2
2
3
x x
x
+ 3 3
3 4 2
x x
x x
( )+
• • •

10. Step 4: Divide out the common factors. In this
case, the common factors divide to become 1.
3 3
3 4 2
x x
x x
( )+
• • •
Step 5: Write in simplified form.
x
x
+ 3
4 2

11. Simplify the following rational expressions.
1
9
2 4
2
2
.
x y z
x y z
2
3
4 32
.
a
a a
+
+ +
3
3 1 5
7 1 02
.
x
x x
−
− +
4
2 1 5
1 2
2
2
.
x x
x x
− −
− −
5
1 4 3 5 2 1
1 2 3 0 1 8
2
2
.
x x
x x
+ +
+ +

12. 9
2 4
2
2
x y z
x y z
= 3 3
3 8
• • • • •
• • • • •
x x y z
x y z z
3
3
• • •
• • •
x y z
x y z
•
3
8
•
•
x
z
1 •
3
8
x
z
= 3
8
x
z
Factor the numerator
and denominator
Divide out the
common factors.
Write in simplified
form.

13. a
a a
+
+ +
3
4 32 = a
a a
+
+ +
3
3 1( ) ( )
Factor the numerator
and denominator
a
a
+
+
3
3
•
1
1a +
1 •
1
1a +
= 1
1a +
Divide out the
common factors.
Write in simplified
form.

14. 3 1 5
7 1 02
x
x x
−
− +
= 3 5
5 2
( )
( ) ( )
x
x x
−
− −
x
x
−
−
5
5
•
3
2x −
1 •
3
2x −
=
3
2x −
Factor the numerator
and denominator
Divide out the
common factors.
Write in simplified
form.

15. x x
x x
2
2
2 1 5
1 2
− −
− −
=
( ) ( )
( ) ( )
x x
x x
− +
− +
5 3
4 3
x
x
+
+
3
3
•
x
x
−
−
5
4
1 •
x
x
−
−
5
4
=
x
x
−
−
5
4
Factor the numerator
and denominator
Divide out the
common factors.
Write in simplified
form.

16. 1 4 3 5 2 1
1 2 3 0 1 8
2
2
x x
x x
+ +
+ +
=
7 2 5 3
6 2 6 3
2
2
( )
( )
x x
x x
+ +
+ +
( )
( )
2 5 3
2 6 3
2
2
x x
x x
+ +
+ +
•
7
6
1 •
7
6
=
7
6
Factor the numerator
and denominator
Divide out the
common factors.
Write in simplified
form.