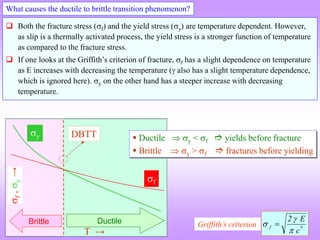
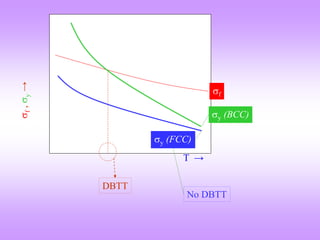
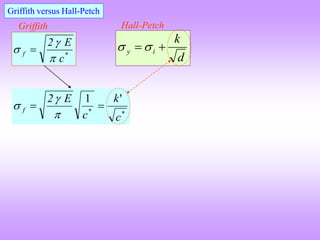
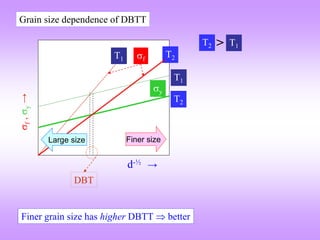
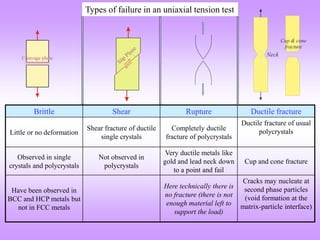
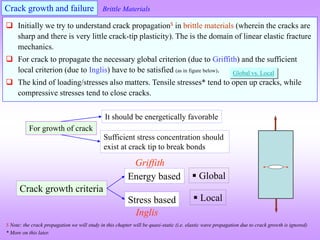
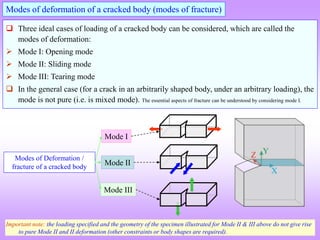
The document provides an overview of fracture mechanics, detailing the difference between brittle and ductile fractures as well as the significance of crack propagation in material failure. It highlights the theoretical strength of materials, the impact of crack geometry, and the factors influencing crack behavior under stress, while outlining the importance of characterizing fracture toughness. Historical context is given, linking concepts to the failures observed in WWII Liberty ships and early significant works in fracture theory.

1. FRACTURE
 Brittle Fracture: criteria for fracture.
 Ductile fracture.
 Ductile to Brittle transition.
Fracture Mechanics
T.L. Anderson
CRC Press, Boca Raton, USA (1995).
Fracture Mechanics
C.T. Sun & Z.-H. Jin
Academic Press, Oxford (2012).
MATERIALS SCIENCE
&
ENGINEERING
Anandh Subramaniam & Kantesh Balani
Materials Science and Engineering (MSE)
Indian Institute of Technology, Kanpur- 208016
Email: anandh@iitk.ac.in, URL: home.iitk.ac.in/~anandh
AN INTRODUCTORY E-BOOK
Part of
http://home.iitk.ac.in/~anandh/E-book.htm
A Learner’s Guide

2. Theoretical fracture strength and cracks
 Let us consider a perfect crystalline material loaded in tension. Failure by fracture can occur
if bonds are broken and fresh surfaces are created.
 If two atomic planes are separated the force required initially increases to a maximum (Fmax)
and then decreases. The maximum stress corresponding to Fmax is the theoretical strength t .
 This stress is given by:
Applied
Force
(F)
→
r →
a0
Cohesive force
0
a
E
t
TFS


 

 E → Young’s modulus of the crystal
  → Surface energy
 a0 → Equilibrium distance between
atomic centres
Fmax
0
 This implies the theoretical fracture strength is in the range of E/10 to E/6*.
 The strength of real materials is of the order of E/100 to E/1000 (i.e. much lower in
magnitude). Tiny cracks are responsible for this (other weak regions in the crystal could also be responsible for this).
 *For Al:
E=70.5 GPa, a0=2.86 Å, (111)= 0.704 N/m.
 t = 13.16 GPa
 Cracks play the same role in fracture (of weakening)
as dislocations play for plastic deformation.
By Energy consideration


2
E
TFS 
By atomistic approach
For many metals  ~ 0.01Ea0

3.  Fracture is related to propagation of cracks, leading to the failure of the
material/component.
 If there are no pre-existing cracks, then a crack needs to nucleate before propagation (to
failure). Crack nucleation$ typically requires higher stress levels than crack propagation.
 A crack is typically a ‘sharp*’ void in a material, which acts like a stress concentrator or
amplifier. Hence, crack is a amplifier of a ‘far field’mean stress. (Cracks themselves do not
produce stresses!). [A crack is a stress amplifier !].
 Cracks in general may have several geometries. Even a circular hole can be considered as a
very ‘blunt’crack. A crack may lie fully enclosed by the material or may have ‘crack faces’
connected to the outer surface.
 Crack propagation leads to the creation of new surface area, which further leads to the
increase in the surface energy of the solid. However, in fracture the surface energy involved
(the fracture surface energy) is typically greater than the intrinsic surface energy as fracture
involves ‘sub-surface’ atoms to some extent. Additionally, the fracture surface energy may
involve terms arising out of energy dissipation due to micro-cracking, phase transformation
and plastic deformation.
Fracture
2a
A crack in a material
Fracture surface energy (f) > Intrinsic surface energy ()
$ Regions of stress concentrations (arising from various sources) ‘help’ in the process.
* More about this sooner
Click here What is meant by failure?

4.  Fracture mechanics is the subject of study, wherein the a materials resistance to fracture is
characterized. In other words the ‘tolerance’ of a material to crack propagation is analyzed.
 Crack propagation can be steady (i.e. slowly increasing crack length with time or load) or
can be catastrophic (unsteady crack propagation, leading to sudden failure of the material)*.
 ‘What dislocation is to slip, crack is to fracture’.
 Under tensile loading if the stress exceeds the yield strength the material, the material
begins to plastically deform. The area under the stress-strain curve is designated as the
toughness in uniaxial tension.
 Similarly, in the presence of cracks we arrive at a material parameter, which characterizes
the toughness of the material in the presence of cracks→ the fracture toughness.
 In most materials, even if the material is macroscopically brittle (i.e. shows very little
plastic deformation in a uniaxial tension test) there might be some ductility at the
microscopic level. This implies that in most materials the crack tip is not ‘infinitely’ sharp,
but is blunted a little. This further avoids the stress singularity at the crack tip as we shall
see later.
Sharp Crack (tip)
Crack after crack tip
blunting process
* One of the important goals of material/component design is to
avoid catastrophic failure. If crack propagation is steady, then we
can practice preventive maintenance (i.e. replace the component
after certain hours of service) → this cannot be done in the case
of catastrophic failure.

5. Breaking
of
Liberty Ships
Cold waters
Welding instead of riveting
High sulphur in steel
Residual stress
Continuity of the structure
Microcracks
 The subject of Fracture mechanics has its origins in the failure of WWII Liberty ships. In
one of the cases the ship virtually broke into two with a loud sound, when it was in the
harbour i.e. not in ‘fighting mode’.
 This was caused by lack of fracture toughness at the weld joint, resulting in the propagation
of ‘brittle’ crack. The full list of factors contributing to this failure is in the figure below.
 The steel of the ship hull underwent a phenomenon known as ‘ductile to brittle transition’
due to the low temperature of the sea water (about which we will learn more in this chapter).

6. 2a
A crack in a material
What is a crack?
Funda Check
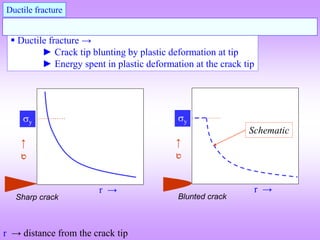
 As we have seen crack is an amplifier of ‘far-field’ mean stress. The sharper the crack-tip,
the higher will be the stresses at the crack-tip. It is a region where atoms are ‘debonded’ and
an internal surface exists (this internal surface may be connected to the external surface).
 Cracks can be sharp in brittle materials, while in ductile materials plastic deformation at the
crack-tip blunts the crack (leading to a lowered stress at the crack tip and further alteration
of nature of the stress distribution).
 Even void or a through hole in the material can be considered a crack. Though often a crack is considered to
be a discontinuity in the material with a ‘sharp’ feature (i.e. the stress amplification factor is large).
 A second phase (usually hard brittle phase) in a lens/needle like geometry can lead to stress
amplification and hence be considered a crack. Further, (in some cases) debonding at the
interface between the second phase and matrix can lead to the formation of an interface
crack.
 As the crack propagates fresh (internal) surface area is created. The fracture surface energy
required for this comes from the strain energy stored in the material (which could further
come from externally applied loads). In ductile materials energy is also expended for plastic
deformation at the crack tip.
 A crack reduces the stiffness of the structure (though this may often be ignored).
Hard second phase in
the material
Though often in figures the crack is shown to have a large lateral
extent, it is usually assumed that the crack does not lead to an
appreciable decrease in the load bearing area [i.e. crack is a local
stress amplifier, rather than a ‘global’ weakener by decreasing
the load bearing area].

7. ~
2a a
Characterization of Cracks
Cracks can be characterized looking into the following aspects.
 Its connection with the external free surface: (i) completely internal, (ii) internal cracks with
connections to the outer surfaces, (iii) Surface cracks.
Cracks with some contact with external surfaces are exposed to outer media and hence may
be prone to oxidation and corrosion (cracking).We will learn about stress corrosion cracking later.
 Crack length (the deleterious effect of a crack further depends on the type of crack (i, ii or
iii as above).
 Crack tip radius (the sharper the crack, the more deleterious it is). Crack tip radius is
dependent of the type of loading and the ductility of the material.
 Crack orientation with respect to geometry and loading.

8. Fracture
Brittle
Ductile
 One of the goals of fracture mechanics is to derive a material property (the fracture
toughness), which can characterize the mechanical behaviour a material with flaws (cracks)
in it.
 Fracture can broadly be classified into Brittle and Ductile fracture. This is usually done
using the macroscopic ductility observed and usually not taking into account the microscale
plasticity, which could be significant. A ductile material is one, which yields before fracture.
 Further, one would like to avoid brittle fracture, wherein crack propagation leading to
failure occurs with very little absorption of energy (in brittle fracture the crack may grow
unstably, without much predictability).
 Three factors have a profound influence on the nature of fracture:
(i) temperature, (ii) strain rate, (iii) the state of stress.
 Materials which behave in a brittle fashion at low temperature may become ductile at high
temperatures. When strain rate is increased (by a few orders of magnitude) a ductile
material may start to behave in a brittle fashion.
Fracture: Important Points
Ductile material : y < f
Promoted by High Strain rate
Triaxial state of State of stress
Low Temperature
Factors affecting
(the nature of) fracture
Strain rate
State of stress
Temperature

9.  Considerable amount of information can be gathered regarding the origin and nature of
fracture by studying the fracture surface.
 The fracture surface has to be maintained in pristine manner (i.e. oxidation, contact damage,
etc. should be avoided) to do fractography.
 It should be noted that a sample which shows very little macroscopic ductility, may display
microscopic ductility (as can be seen in a fractograph).
 Truly brittle samples show faceted cleavage planes, while ductile fracture surface displays a
dimpled appearance.
Fractography
Fracture surface as seen in an SEM*
* The Scanning Electron Microscope (SEM) with a large depth of field is an ideal tool to do fractography.

10. Behaviour described Terms Used
Crystallographic mode Shear Cleavage
Appearance of Fracture surface Fibrous Granular / bright
Strain to fracture Ductile Brittle
Path Transgranular Intergranular
 Fracture can be classified based on: (i) Crystallographic mode, (ii) Appearance of Fracture
surface, (iii) Strain to fracture, (iv) Crack Path, etc. (As in the table below).
 Presence of chemical species at the crack tip can lead to reduced fracture stress and
enhanced crack propagation.
Classification of Fracture (based on various features)

11. Brittle Shear Rupture Ductile fracture
Little or no deformation
Shear fracture of ductile
single crystals
Completely ductile
fracture of polycrystals
Ductile fracture of usual
polycrystals
Observed in single
crystals and polycrystals
Not observed in
polycrystals
Very ductile metals like
gold and lead neck down
to a point and fail
Cup and cone fracture
Have been observed in
BCC and HCP metals but
not in FCC metals
Here technically there is
no fracture (there is not
enough material left to
support the load)
Cracks may nucleate at
second phase particles
(void formation at the
matrix-particle interface)
Slip
Plane
Cleavage plane
Cleavage plane
Types of failure in an uniaxial tension test

12. ‘Early Days’ of the Study of Fracture
  C.E. Inglis (seminal paper in 1913)[1]
 A.A. Griffith (seminal paper in 1920)[2]
 Stress based criterion for crack growth (local)
→ C.E. Inglis.
 Energy based criterion for crack growth (global)
→ A.A. Griffith (Work done on glass very brittle material).
[1] C.E. Inglis, Stresses in a plate due to the presence of cracks and sharp corners, Trans. Inst. Naval Architechts 55 (1913) 219-230.
[2] A.A. Griffith, The phenomena of rupture and flow in solids, Philos. Trans. R. Soc. Lond. A221 (1920) 163-198. → Fat paper!

13. Crack growth and failure
Crack growth criteria
Stress based
Energy based  Global
 Local
Griffith
Inglis
 Initially we try to understand crack propagation$ in brittle materials (wherein the cracks are
sharp and there is very little crack-tip plasticity). The is the domain of linear elastic fracture
mechanics.
 For crack to propagate the necessary global criterion (due to Griffith) and the sufficient
local criterion (due to Inglis) have to be satisfied (as in figure below).
 The kind of loading/stresses also matters. Tensile stresses* tend to open up cracks, while
compressive stresses tend to close cracks.
Global vs. Local
For growth of crack
Sufficient stress concentration should
exist at crack tip to break bonds
It should be energetically favorable
$ Note: the crack propagation we will study in this chapter will be quasi-static (i.e. elastic wave propagation due to crack growth is ignored)
* More on this later.
Brittle Materials

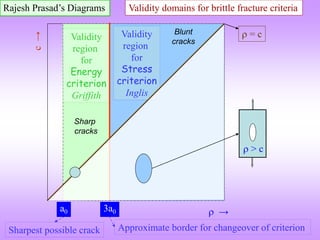
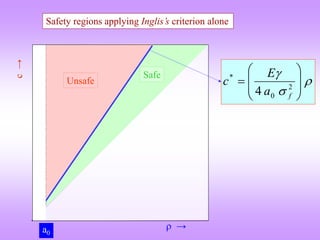
14. Stress based criterion for crack propagation (Inglis criterion)
 In 1913 Inglis observed that the stress concentration around a hole (or a ‘notch’) depended
on the radius of curvature of the notch. I.e. the far field stress (0) is amplified near the hole.
[(max / 0) is the stress concentration factor ()].
 A ‘flattened’ (elliptical) hole can be thought of as a crack.









c
σ
σ 2
1
0
max
 0 → applied “far field” stress
 max → stress at hole/crack tip
  → hole/crack tip radius
 c → length of the hole/crack

c
σ
σ 0
max 2

0
max


σ

 A circular hole has a stress concentration factor of 3 [ = 3].
 From Inglis’s formula it is seen that the ratio of crack length to crack tip radius is important
and not just the length of the crack.
hole crack
Sharper the crack, higher the stress concentration.
For sharp cracks
 = c
For a circular hole








c
c
σ
σ 2
1
0
max
0
max 3σ
σ 
 One way of understanding this formula is that if max
exceeds t (the theoretical fracture stress), then the
material fails.
 This is in spite of the fact that the applied stress is of
much lower magnitude than the theoretical fracture
stress.

15. E
cohesive

 
c
a
E
f
0
4

 
 For a crack to propagate the crack-tip stresses have to do work to break the bonds at the
crack-tip. This implies that the ‘cohesive energy’ has to be overcome.
 If there is no plastic deformation or any other mechanism of dissipation of energy, the work
done (energy) appears as the surface energy (of the crack faces).
 The fracture stress (f) (which is the ‘far field’applied stress) can be computed using this
approach.
 f → fracture stress (applied “far-field”)
  → crack tip radius
 c → length of the crack
 a0 → Interatomic spacing

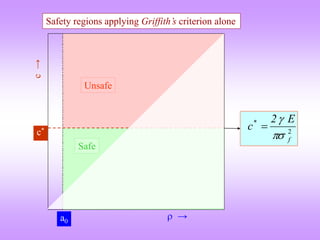
16. Griffith’s criterion for brittle crack propagation
 We have noted that the crack length does not appear ‘independently’ (of the crack tip radius)
in Inglis’s formula. Intuitively we can feel that longer crack must be more deleterious.
 Another point noteworthy in Inglis’s approach is the implicit assumption that sufficient
energy is available in the elastic body to do work to propagate the crack.  (‘What if there is
insufficient energy?’)  (‘What if there is no crack in the body?’). Also, intuitively we can
understand that the energy (which is the elastic energy stored in the body) should be
available in the proximity of the crack tip (i.e. energy available far away from the crack tip
is of no use!).
 Keeping some of these factors in view, Griffith proposed conditions for crack propagation:
(i) bonds at the crack tip must be stressed to the point of failure (as in Inglis’s criterion),
(ii) the amount of strain energy released (by the ‘slight’ unloading of the body due to crack
extension) must be greater than or equal to the surface energy of the crack faces created.
 The second condition can be written as:
dc
dU
dc
dUs 

 Us → strain energy
 U → surface energy
(Energy per unit area: [J/m2])
 dc → (‘infinitesimal’) increase in the
length of the crack (‘c’ is the crack length)
We look at the formulae for Us and U next.
Essentially this is like energy balance (with the ‘=‘ sign) → the surface energy for the extended
crack faces comes from the elastically stored energy (in the fixed displacement case)

17.  The strain energy released on the introduction of a very narrow elliptical double ended
crack of length ‘2c’ in a infinite plate of unit width (depth), under an uniform stress a is
given by the formula as below.
  E
U
U
U a
crack
with
crack
without
2
2
s
c
U
energy
elastic
in
Reduction








 This is because the body with the crack has a lower elastic
energy stored in it as compared to the body without the crack
(additionally, the body with the crack is less stiffer). Also, the
assumption is that the introduction of a crack does not alter
the far-field stresses (or the load bearing area significantly).
 Notes:
 The units of Us is [J/m] (Joules per meter depth of the crack→ as
this is a through crack).
 Though Us has a symbol of energy, it is actually a difference
between two energies
(i.e. two states of a body→ one with a crack and one without).
 Half crack length ‘c’ appears in the formula.
 E is assumed constant in the process (the apparent modulus will decrease
slightly).
 a is the ‘far field’ stress (this may result from displacements
rather than from applied forces see note later).
Should be written with a ve
sign if U = (Ufinal  Uinitial)
For now we assume that these stresses
arise out of ‘applied’ displacements

18.  The computation of the actual energy released is more involved and is given by the formula
as noted before:
 The formula for Us can be appreciated by considering the energy released from a circular
region of diameter 2c as in the figure below. (The region is cylindrical in 3D).
 The energy released is:
 
2
2
region
circular
s c
2
1
U
region
circular
a
from
released
energy
Elastic 

E
a


E
a
2
2
s
c
U



Energy released from this circular region
is given by the formula (1) as above
(not a true value, but to get a feel of the
predominant region involved).
(1)
 For a body in plane strain condition (i.e. ~ thick in the z-direction, into the plane of the
page), E is replaced with E/(12)
 
)
1
(
c
U 2
2
2
s





E
a
Plane stress condition
Plane strain condition
E
a
2
s c
2
c
U 




Hence

19.  The surface energy of the crack of length 2c & unit width/depth is:
c
γ
U f
4
energy
surface
Fracture 
 
 This is the difference in the energy between a body with a crack and one without a crack.
 As pointed out before, the surface energy is the fracture surface energy and not just the
surface free energy. The origin of this energy is contributions from dissipative mechanisms
like plastic deformation, micro-cracking & phase transformation, in addition to the energy
of the ‘broken bonds’.
 The units are Joules per meter depth of the body: [J/m].
[J/m]
Important note
 The “Griffith experiment” is easily understood in displacement control mode (i.e. apply a
constant displacement and ‘see’ what happens to the crack) and is more difficult to
comprehend in the force control mode (by applying constant ‘far-field’ forces).
 In force control mode, the forces do work on the system and hence the ‘energy accounting’
process is more involved.
 Hence, it is better to visualize  as arising from a ‘far field’ applied displacements.
c
f


2
c
U




20.  Now we have the formulae for Us & U to write down the Griffith’s condition:
dc
dU
dc
dUs 
 f
a
E



2
c 2

 LHS increases linearly with c, while RHS is constant.
 The ‘equal to’ (=) represents the bare minimum requirement (i.e. the critical condition) →
the minimum crack size, which will propagate with a ‘balance’ in energy (i.e. between
elastic energy released due to crack extension and the penalty in terms of the fracture
surface energy).
 The critical crack size (c*): (Note that ‘c’is half the crack length internal)
 A crack below this critical size will not propagate under a constant stress a.
 Weather a crack of size greater than or equal to c* will propagate will depend on the Inglis
condition being satisfied at the crack-tip.
 This stress a now becomes the fracture stress (f)→ cracks of length c* will grow
(unstably) if the stress exceeds f (= a)
2
* 2
a
f
E
c



*
f
c
E
2


 
At constant c (= c*)
when  exceeds f then specimen fails
Griffith )
1
(
c
E
2
2
*






f
Plane strain conditions
 E
a
2
s c
2
c
U 




c
f


2
c
U




21.   

















E
a
f
2
2
c
c
4
U
crack
a
of
on
introducti
the
on
energy
in
Change



c →
U
→
0
*






 
c
dc
U
d
*
c
0
c
0
0
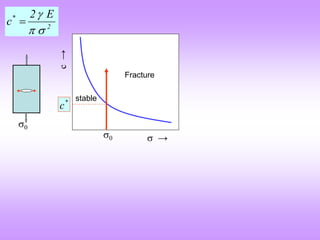
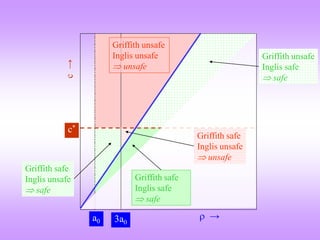
An alternate way of understanding the Griffith’s criterion (energy based)
c
γ
U f
4


E
a
2
2
s
c
U



 This change in energy (U) should be negative with an increase in crack
length (or at worst equal to zero). I.e. (dU/dc) ≤ 0.
 At c* the slope of U vs c curve is zero [(dU/dc)c* = 0]. This is a point
of unstable equilibrium.
 With increasing stress the value of c* decreases (as expected→ more
elastic strain energy stored in the material).
Stable
cracks Unstable cracks
For ready reference
Negative slope
Positive slope
c →
U
→
*
1
c *
2
c

22. Griffith versus Inglis criteria
c
a
E
f
0
4

 
Inglis
*
f
c
E
2


 
Griffith
result
same
the
give
criterion
Inglis
and
s
Griffith'
8a
If 0

 
0
3a Griffith's and Inglis criterion give the same result
the 'Dieter' cross-over criterion
If  

2
f
* E
2
c


 


a
E
c
f








 2
0
*
4
 For very sharp cracks, the available elastic energy near the crack-tip, will determine if the
crack will grow.
 On the other hand if available energy is sufficient, then the ‘sharpness’ of the crack-tip will
determine if the crack will grow.
A sharp crack is limited by availability of energy, while a blunt crack is limited by stress concentration.

24. ‘Modern’ Fracture Mechanics
 G.R. Irwin[1]
 Stress Intensity Factor (K)
Material Parameter  Fracture Toughness (KC)
 Energy Release Rate (G)
Material Parameter  Critical Energy Release Rate (GC)
 J-integral
[1] G.R. Irwin, “Fracture Dynamics”, in: “Fracture of Metals”, ASM, Cleaveland, OH, 1948, pp.147-166.
[2] G.R. Irwin, “Analysis of stresses and strains near the end of a crack traversing a plate, J. Appl. Mech 24 (1957) 361-364.

25.  Historically (in the ‘old times’ ~1910-20) fracture was studied using the Inglis and Griffith
criteria.
 The birth of fracture mechanics (~1950+) led to the concepts of stress intensity factor (K)
and energy release rate (G). Due to Irwin and others.
Fracture Mechanics

26.  G is defined as the total potential energy () decrease during unit crack extension (dc):
Concept of Energy Release Rate (G)
dc
d
G



The potential energy is a difficult quantity to visualize. In the absence of external
tractions (i.e. only displacement boundary conditions are imposed), the potential
energy is equal to the strain energy stored:  = Us.*
* It is better to understand the basics of fracture with fixed boundary conditions (without any surface tractions).
dc
dU
G s

 With displacement boundary conditions only
 Crack growth occurs if G exceeds (or at least equal to) a critical value GC:
C
G
G  For perfectly brittle solids: GC = 2f (i.e. this is equivalent to Griffith’s criterion).

28. Mode I
Mode III
Modes of Deformation /
fracture of a cracked body
Mode II
 Three ideal cases of loading of a cracked body can be considered, which are called the
modes of deformation:
 Mode I: Opening mode
 Mode II: Sliding mode
 Mode III: Tearing mode
 In the general case (for a crack in an arbitrarily shaped body, under an arbitrary loading), the
mode is not pure (i.e. is mixed mode). The essential aspects of fracture can be understood by considering mode I.
Modes of deformation of a cracked body (modes of fracture)
Important note: the loading specified and the geometry of the specimen illustrated for Mode II & III above do not give rise
to pure Mode II and II deformation (other constraints or body shapes are required).

29. Stress fields at crack tips
 For a body subjected far field biaxial stress 0, with a double ended crack of length 2c, the
stress state is given by:


























2
3
2
1
2
2




 Sin
Sin
Cos
r
KI
xx


























2
3
2
1
2
2




 Sin
Sin
Cos
r
KI
yy



















2
3
2
2
2




 Sin
Sin
Cos
r
KI
xy
 Note the inverse square root (of r) singularity at the crack tip. The intensity of the
singularity is captured by KI (the Stress Intensity Factor).
 As no material can withstand infinite stresses (in ductile materials plasticity will intervene),
clearly the solutions are not valid exactly at (& ‘very near’) the crack tip.
 At  = 0 and r → the stresses (xx & yy) should tend to 0. This is not the case, as seen
from the equations ((1) & (2)). This implies that the equations should be used only close to
crack tip (with little errors) or additional terms must be used.
(1)
(2)
(3)
Fig.1

30. Understanding the stress field equation


























2
3
2
1
2
2




 Sin
Sin
Cos
r
KI
xx
r
f
KI
xx



2
)
(

→
 
c
Y
KI 
0

‘Shape factor’ related to ‘Geometry’
Indicates mode I ‘loading’
Half the crack length
 “KI (the Stress Intensity Factor) quantifies the magnitude of the effect of stress singularity at
the crack tip”[1].
 Quadrupling the crack length is equivalent to doubling the stress ‘applied’. Hence, K
captures the combined effect of crack length and loading. The remaining part in equation(1)
is purely the location of a point in (r, ) coordinates (where the stress has to be computed).
 Note that there is no crack tip radius () in the equation! The assumptions used in the
derivation of equations (1-3) are:   = 0,  infinite body,  biaxial loading.
 ‘Y’ is considered in the next page.
[1] Anthony C. Fischer-Cripps, “Introduction to Contact Mechanics”, Springer, 2007.
(1)

31. The Shape factor (Y)
 It is obvious that the geometry of the crack and its relation to the body will play an
important role on its effect on fracture.
 The factor Y depends on the geometry of the specimen with the crack.
 Y=1 for the body considered in Fig.1 (double ended crack in a infinite body).
 Y=1.12 for a surface crack. The value of Y is larger (by 12%) for a surface crack as
additional strain energy is released (in the region marked in orange colour in the figure
below), due to the presence of the free surface.
 Y=2/ for a embedded penny shaped crack.
 Y=0.713 for a surface half-penny crack.

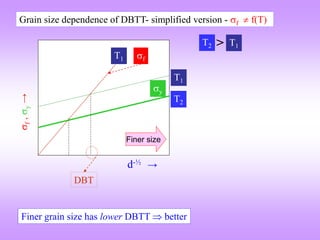
32. Summary of Fracture Criteria
Criterion named after &
[important quantities]
Comments Fracture occurs if Relevant formulae
Inglis Involves crack tip radius
Griffith Involves crack length
Irwin [K] Concept of stress intensity factor.
KI > KIC
(in mode I)
- [G]
Energy release rate based. Same as K based
criterion for elastic bodies.

33.  The crack tip fields consists of two parts: (i) singular part (which blow up near the crack tip)
and (ii) the non-singular part.
 The region near the crack tip, where the singular part can describe the stress fields is the K-
Dominance region. This is the region where the stress intensity factor can be used to
characterize the crack tip stress fields.
Region of K-Dominance

34.  One of the important goals of fracture mechanics is to derive a material parameter, which
characterizes cracks in a material. This will be akin to yield stress (y) in a uniaxial tension
test (i.e. y is the critical value of stress, which if exceeded (  y) then yielding occurs).
 The criterion for fracture in mode I can be written as:
Fracture Toughness (Irwins’s K- Based)
IC
I K
K  Where, KIC is the critical value of stress intensity factor (K) and is known
as Fracture Toughness
 KIC is a material property (like yield stress) and can be determined for different materials
using standard testing methods. KIC is a microstructure sensitive property.
 The focus here is the ‘local’ crack tip region and not ‘global’, as in the case of Griffith’s
approach.
 All the restrictions/assumptions on K will apply to KIC: (i) material has a liner elastic
behaviour (i.e. no plastic deformation or other non-linear behaviour), (ii) inverse square root
singularity exists at crack tip (eq. (1)), (iii) the K-dominance region characterizes the crack
tip.
r
f
KI
xx



2
)
(
 (1)

35. Material KIC [MPam]**
Cast Iron 33
Low carbon steel 77
Stainless steel 220
Al alloy 2024-T3 33
Al alloy 7075-T6 28
Ti-6Al-4V 55
Inconel 600 (Ni based alloy) 110
* We have already noted that fracture toughness is a microstructure sensitive property and hence to get ‘true’value the
microstructure has to be specified.
** Note the strange units for fracture toughness!
[1] Fracture Mechanics, C.T. Sun & Z.-H. Jin, Academic Press, Oxford (2012).
Fracture Toughness* (KIC) for some typical materials [1]

36. Is KIC really a material property like y?
Funda Check
 Ideally, we would like KIC (in mode I loading, KIIC & KIIIC will be the corresponding
material properties under other modes of loading$) to be a material property, independent of
the geometry of the specimen*. In reality, KIC depends on the specimen geometry and
loading conditions.
 The value KIC is especially sensitive to the thickness of the specimen. A thick specimen
represents a state that is closer to plane strain condition, which tends to suppress plastic
deformation and hence promotes crack growth (i.e. the experimentally determined value of
KIC will be lower for a body in plane strain condition). On the other hand, if the specimen is
thin (small value ‘t’ in the figure), plastic deformation can take place and hence the
measured KIC will be higher (in this case if the extent of plastic deformation is large then KI
will no longer be a parameter which characterizes the crack tip accurately).
$ Without reference to mode we can call it KC.
* E.g. Young’s modulus is a material property independent of the geometry of the specimen, while stiffness is the equivalent ‘specimen geometry
dependent’ property..
 To use KIC as a design parameter, we have to use its ‘conservative
value’. Hence, a minimum thickness is prescribed in the standard
sample for the determination of fracture toughness.
 This implies that KIC is the value determined from ‘plane strain tests’.

37. I seem totally messed up with respect to the proliferation of fracture criteria!
How do I understand all this?
 Essentially there are two approaches: global (energy based) and local (stress based).
 For linear elastic materials the energy and stress field approaches can be considered
equivalent.
Q & A

38.  In ductile materials:
 Crack-tip stresses lead to plastic deformation at the crack-tip, which further leads to crack
tip blunting.
 Energy is consumed due to plastic deformation at the crack-tip (which comes from elastic
strain energy). This implies less energy is available for crack growth (& creation of new surfaces).
 Crack-tip blunting leads to a reduced stress amplification at the crack-tip. Blunting will
avoid ‘stress singularity’ at the crack tip and may lead to a maximum stress at a certain
distance from the crack-tip (as in the figure below).
 Crack-tip blunting will lead to an increased resistance to crack propagation (i.e. increased
fracture toughness).
Ductile fracture
* Note: For a material to be classified as ductile it need not
display large strain in a tensile test.
r r

39. What happens to a ‘crack’ in a ductile material?
Funda Check
 High magnitude of crack tip stresses can cause yielding at the crack tip (plastic
deformation).
 This leads to crack tip blunting, which reduces the stress amplification.
 There develops a zone ahead of the crack tip known as the process zone.
What else can happen at the crack tip due to high stresses?
Funda Check
 High magnitude of crack tip stresses can cause:
 phase transformation (tetragonal to monoclinic phase in Yttria stabilized Zirconia),

40. E
c
c
)
(
4
U
energy
in
Change
2
2
p
s



 




*
p
s
f
c
E
)
(
2






Orowan’s modification to the Griffith’s equation to include “plastic energy”
2
3
2
)
10
10
(
~
)
2
1
(
~
J/m
J/m
p
2
s




*
p
f
c
E
2


 

42. Ductile – brittle transition
 Certain materials which are ductile at a given temperature (say room temperature), become
brittle at lower temperatures. The temperature at which this happens is terms as the Ductile
Brittle Transition Temperature (DBTT).
 As obvious, DBT can cause problems in components, which operate in ambient and low
temperature conditions.
 Typically the phenomena is reported in polycrystalline materials. Deformation should be
continuous across grain boundary in polycrystals for them to be ductile. This implies that
five independent slip systems should be operatiave (this is absent in HCP and ionic
materials).
 This phenomenon (ductile to brittle transition) is not observed in FCC metals (they remain
ductile to low temperatures).
 Common BCC metals become brittle at low temperatures (as noted before a decrease in
temperature can be visualized as an increase in strain rate, in terms of the effect on the
mechanical behaviour).
 As we have noted before a ductile material is one which yields before fracture (i.e. its yield
strength is lower in magnitude than its fracture strength).

43.  Both the fracture stress (f) and the yield stress (y) are temperature dependent. However,
as slip is a thermally activated process, the yield stress is a stronger function of temperature
as compared to the fracture stress.
 If one looks at the Griffith’s criterion of fracture, f has a slight dependence on temperature
as E increases with decreasing the temperature ( also has a slight temperature dependence,
which is ignored here). y on the other hand has a steeper increase with decreasing
temperature.
What causes the ductile to brittle transition phenomenon?

f
,

y
→
y
T →
f
DBTT
Ductile
Brittle
 Ductile  y < f  yields before fracture
 Brittle  y > f  fractures before yielding
*
f
c
E
2


 
Griffith’s criterion

44. c
a
E
f
0
4

 
Inglis

45. 
f
,

y
→
y (BCC)
T →
f
DBTT
y (FCC)
No DBTT

46. Griffith versus Hall-Petch
*
f
c
E
2


 
d
k
i
y 
 

Griffith Hall-Petch
*
'
1
c
k
c
E
2
*
f 





47. 
f
,

y
→
y
d-½ →
DBT
T1
T2
T1
T2
f
Grain size dependence of DBTT
Finer size
Large size
Finer grain size has higher DBTT  better
T1
T2 >

48. 
f
,

y
→
y
d-½ →
DBT
T1
T2
T1 f
Grain size dependence of DBTT- simplified version - f  f(T)
Finer size
Finer grain size has lower DBTT  better
T1
T2 >

49. Protection against brittle fracture
 ↓  f ↓  done by chemical adsorbtion of molecules
on the crack surfaces
 Removal of surface cracks  etching of glass
(followed by resin cover)
 Introducing compressive stresses on the surface
 Surface of molten glass solidified by cold air followed by
solidification of the bulk (tempered glass)
→ fracture strength can be increased 2-3 times
 Ion exchange method → smaller cations like Na+ in sodium
silicate glass are replaced by larger cations like K+ on the
surface of glass → higher compressive stresses than tempering
 Shot peening
 Carburizing and Nitriding
 Pre-stressed concrete
*
f
c
E
2


 

50.  Cracks developed during grinding of ceramics extend upto one grain
 use fine grained ceramics (grain size ~ 0.1 m)
 Avoid brittle continuous phase along the grain boundaries
→ path for intergranular fracture (e.g. iron sulphide film along
grain boundaries in steels → Mn added to steel to form spherical
manganese sulphide)

51. Conditions of fracture
Torsion
Fatigue
Tension
Creep
Low temperature Brittle fracture
Temper embrittlement
Hydrogen embrittlement

52. Why do we need a large ductility (say more than 10% tensile elongation)
material, while ‘never’ actually in service component is going to see/need such
large plastic deformation (without the component being classified as ‘failed’).
Funda Check
 Let us take a gear wheel for an example. The matching tolerances between gears are so
small that this kind of plastic deformation is clearly not acceptable.
 In the case of the case carburized gear wheel, the surface is made hard and the interior is
kept ductile (and tough).
 The reason we need such high values of ductility is so that the crack tip gets blunted and the
crack tip stress values are reduced (thus avoiding crack propagation).

53.  →
c
→
Fracture
stable
E
2
c 2
*




*
c
0
0

54. Rajesh Prasad’s Diagrams Validity domains for brittle fracture criteria
Sharpest possible crack Approximate border for changeover of criterion
 →
c
→
a0 3a0
Validity
region
for
Energy
criterion
Griffith
Validity
region
for
Stress
criterion
Inglis
Sharp
cracks
Blunt
cracks
 > c
 = c

55.  →
c
→
a0
c*
Safety regions applying Griffith’s criterion alone
Unsafe
Safe
2
f
* E
2
c




56. Unsafe
Safe
 →
c
→
a0
Safety regions applying Inglis’s criterion alone



a
E
c
f








 2
0
*
4

57.  →
c
→
a0
c*
3a0
Griffith safe
Inglis unsafe
 safe
Griffith unsafe
Inglis safe
 safe
Griffith safe
Inglis unsafe
 unsafe
Griffith unsafe
Inglis unsafe
 unsafe
Griffith safe
Inglis safe
 safe

58. Role of Environment in Fracture
 Stress Corrosion Cracking
 Hydrogen Embrittlement

59.  In stress corrosion cracking the presence of a chemical species can enhance crack
propagation and reduce fracture stress. This phenomenon can lead to sudden failure of
ductile metals, especially at high temperatures. The interplay between stress and corrosion is important here.
 The chemical agent is one which is normally corrosive to the metal/alloy* involved. Certain
combinations of metals and chemicals can lead to disastrous effects (i.e. the good news is that not all
combinations are that bad).
 Similar to a critical value of the stress intensity factor (KIC) in normal fracture mechanics,
we can define a critical stress intensity factor in the presence of a corrosive environment (at the
crack tip) (KISCC). This value as seen from the table below can be much lower than KIC.
 Severe accidents like the explosion of boilers, rupture of
gas pipes, etc. have happened due to this phenomenon.
Stress Corrosion Cracking (SCC)
* Metals are considered here, although other materials are also prone to such effects.
Sudden crack growth on exceeding KISCC
 Unlike KIC, KISCC is not a pure material parameter and is
affected by environmental variables (hence for each environment-
material pair the appropriate KISCC value has to be used).

60. Alloy
KIC
(MN/m3/2)
SCC
environment
KISCC
(MN/m3/2)
13Cr steel 60 3% NaCl 12
18Cr-8Ni 200 42% MgCl2 10
Cu-30Zn 200 NH4OH, pH7 1
Al-3Mg-7Zn 25 Aqueous halides 5
Ti-6Al-1V 60 0.6M KCl 20
http://en.wikipedia.org/wiki/Stress_corrosion_cracking

61.  Another related phenomenon, which can be classified under the broad ambit of SCC is
hydrogen embrittlement.
 Hydrogen may be introduced into the material during processing (welding, pickling,
electroplating, etc.) or in service (from nuclear reactors, corrosive environments, etc.).

63. Q & A What are the characteristics of brittle fracture
Extreme case scenario is considered here:
 Cracks are sharp & no crack tip blunting.
 No energy spent in plastic deformation at the crack tip.
 Fracture surfaces are flat.

64. Q & A What is the difference between plane stress and plane strain as far as fracture goes?
 C

66.  Ductile fracture →
► Crack tip blunting by plastic deformation at tip
► Energy spent in plastic deformation at the crack tip
Ductile fracture

→
y
r →

→
y
r →
Sharp crack Blunted crack
Schematic
r → distance from the crack tip