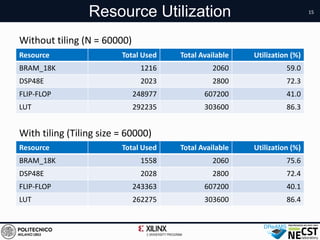
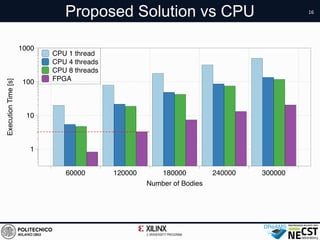
This document describes a hardware acceleration approach for N-body simulations using an FPGA. It presents a semi-dataflow architecture and tiling technique to efficiently compute pairwise forces with reduced data transfers. Evaluation shows the FPGA implementation achieves 4400 million particle-pairs per second, outperforming a CPU and achieving high performance per watt compared to other platforms. Future work involves connecting to the host via PCIe and further optimizing performance per watt.

1. bibbidi N-BObbiDY boo
Magic Acceleration of N-Body Simulation
E. Del Sozzo, M. Rabozzi, M. Nanni, M. D. Santambrogio
emanuele.delsozzo@polimi.it
marco.rabozzi@polimi.it
marco3.nanni@mail.polimi.it
marco.santambrogio@polimi.it
Xilinx Open Hardware 2017 Contest

2. N-Body Simulation 2
F1,2
F1,3
F2,1
F3,1
F2,3
F3,2

3. N-Body Simulation 3

4. A highly scalable and efficient parallel design
for All-Pairs N-Body simulation on FPGA
4
Proposed Solution
semi-dataflow architecture tiling approach

5. 1. Hardware/Software Partitioning
2. Data transfer
3. Semi-dataflow architecture
4. Tiling
5
Implementation

6. Algorithm Overview 6
for each timestep t do
for each body i do
for each body j, j≠i do
PairwiseForce(i,j)
end for
UpdateBody(i)
end for
end for
F1,2
F1,3
F2,1
F2,3
F3,1
F3,2
𝑂(𝑁2
)

7. 7
Force Computation
• Generalize the computation on FPGA
• Save resources

8. 1. Hardware/Software Partitioning
2. Data transfer
3. Semi-dataflow architecture
4. Tiling
8
Implementation

9. • Main issues:
• High amount of data to provide to the accelerator for each
body (i.e. positions, charges)
• A pure dataflow approach would imply a massive memory
traffic
• Store bodies on FPGA BRAMs
• Exploit memory burst
• Reduce memory traffic
• Data packing (512 bits)
9
Data Transfer

10. 1. Hardware/Software Partitioning
2. Data transfer
3. Semi-dataflow architecture
4. Tiling
10
Implementation

11. 11
Semi-Dataflow Architecture
high performance
improvement

12. 1. Hardware/Software Partitioning
2. Data transfer
3. Semi-dataflow architecture
4. Tiling
12
Implementation

13. 13
Tiling
n-body kernel
(48 x 2-body core)
+
TileBuffer I
( position of bodies
to update)
DDR
TileBuffer J
( position and chargeof
referencebodies)
TileBuffer O
||ri j || ||ri j ||
whereG isthegravitational constant,mi isthemassof body i,
and ri j = ri − rj istheposition vector from body i and j. Thisop-
eration, repeated for each body j, wherej , i, may besummarized
asfollows:
TotPairwiseForce(i) =
X
j , i
PairwiseForce(i,j) =
= Gmi ·
X
j , i
mj ri j
||ri j ||3
(2)
Generally,in thecontext of astrophysical simulations,asoftening
factor 2 > 0 isadded to thedenominator [5]. Thepurposeof this
factor isto avoid collisionsbetween bodies, which isreasonableif
thebodiesrepresent galaxies. Asaconsequence, Equation (2) may
berewritten asfollows:
TotPairwiseForce(i) ⇡ Gmi ·
X
j
mj ri j
(||ri j ||2 + 2)3/ 2
8i (3)
1.2 UpdateBody
The second computational step of the simulation updates the in-
formation about position and velocity of each body within the
system. In particular, thesimulation updatesabody by meansof
itstotal pairwiseforceusing an integrator over asmall timestep
dt. To thisend, in order to integrateover time, thesimulation com-
putes the acceleration vector a of each body i starting from the
Tot Pai r wi seFor ce asfollows:
ai ⇡ G ·
X
j
cj ri j
(||ri j ||2 + 2)3/ 2
8i (4)
Then, thesimulation computestheposition r and velocity v of
body i at timet thanksto theacceleration a and thepreviousr and
v, aswell asintegration timestep dt. Heretheformulasdescribing
der to understand what were the main b
mentation. As we expected, the outcom
identi ed the computation of Tot Pai r w
asthebottleneck of All-Pairsapproach. A
hardware-accelerateTot Pai r wi seFor ce
ing in software the Updat eBody functio
have a general implementation on Field
ray (FPGA) suitablefor all theapplicatio
welightly modi ed both theoutput of To
asUpdat eBody function. Thus, theresult
thefollowing:
outi =
X
j , i
cj ri j
(||ri j ||2 +
wherecj isageneric forcecharge(e.g.
tational eld, acoulomb chargein caseof
a consequence, the new formulas of the
following:
8>>>><
>>>>
:
ai (t) = K · ci
mi
·outi (t
vi (t) = vi (t − 1) + ai (
ri (t) = ri (t − 1) + vi (t
whereK istheconstant typical of cert
tional constant, Coulomb constant). Of co
contest, wejust need to multiply for theg
decided to modify thecodein such away
rst of all, to makethecomputation on th
sible,then to avoid sendingunnecessary d
consequence, saving resources(likeDSPs
when apply tiling).Finally,K· ci
mi
can beea
pliedtotheUpdat eBody function.Themo
approach isreported in Algorithm 2, whe
refersto our hardwareacceleration proce

14. 14
Results

15. Resource Total Used Total Available Utilization (%)
BRAM_18K 1558 2060 75.6
DSP48E 2028 2800 72.4
FLIP-FLOP 243363 607200 40.1
LUT 262275 303600 86.4
15
Resource Utilization
Resource Total Used Total Available Utilization (%)
BRAM_18K 1216 2060 59.0
DSP48E 2023 2800 72.3
FLIP-FLOP 248977 607200 41.0
LUT 292235 303600 86.3
Without tiling (N = 60000)
With tiling (Tiling size = 60000)

16. 16
Proposed Solution vs CPU

17. 17
Proposed Solution vs SoA
Platform Type
Cores /
Pipelines
Performance Performance/Power
Ref.
[Mpairs/s] [GFLOPS] [Mpairs/s/W] [GFLOPS/W]
Grape-8 ASIC 2 x 48 - 2 x 480 - 20.5 [4]
Intel i7-6700 CPU 4 766.90 13.80 11.80 0.212
Tegra Kepler GPU 192 192.0 - 96 - [5]
Tesla K80 GPU 2 x 2496 6312 - 63.12 - [5]
8800GTX GPU - ~ 1500 - - - [6]
Cyclone II FPGA 16 - 15.39 - - [7]
Zynq-7020 FPGA 9 1200.5 - 923.46* - [5]
Vectis MAX3 FPGA 1 2978 - 21.3 - [8]
VC707 FPGA 48 4400.45 79.21 220.02 3.96
*Computed from FPGA power consumption only
~ 92% of theoretical performance

18. Future Works
• Connection on the host via PCIe
18
• Improve the design and
enhance performance/watt
• All-pairs n-body simulation demo
Barnes-Hut gravity 200k n-body simulation galaxy

19. Thanks for your attention 19
Bibbidi N-Bobbidy boo at NECST
(https://www.facebook.com/BibbidiNBobbidyboo/)
Bibbidy N-BObbiDY boo at NECST
(https://www.slideshare.net/bibbidyN-BObbiDYboo)
Emanuele Del Sozzo
emanuele.delsozzo@polimi.it
Marco Rabozzi
marco.rabozzi@polimi.it
Marco Nanni
marco3.nanni@mail.polimi.it
Marco D. Santambrogio
marco.santambrogio@polimi.it
@N_BodyAtNECST
(https://twitter.com/N_BodyAtNECST)