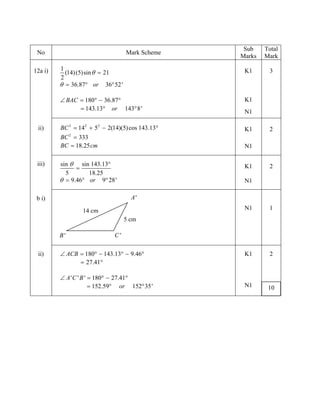
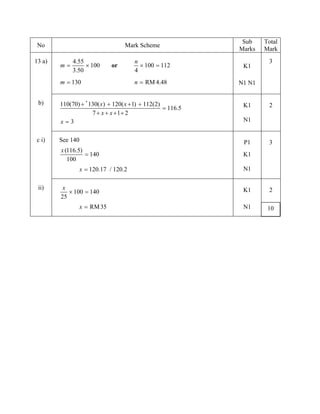
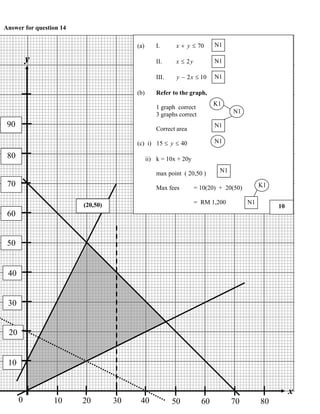
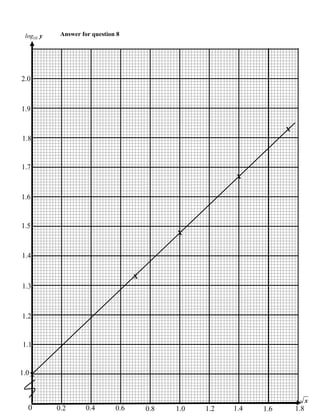
1. The document is a mark scheme for an Additional Mathematics exam that provides the solutions and workings for 8 multiple choice questions. 2. It lists the mark allocation for each part of the questions and shows the step-by-step workings to achieve the full marks. 3. The questions cover topics like algebra, calculus, geometry, sequences and series, and logarithms.

1. SPM TRIAL EXAM 2010
MARK SCHEME ADDITIONAL MATHEMATICS PAPER 2
SECTION A (40 MARKS)
No. Mark Scheme Total
Marks
1 x = 1− 2y P1
2(1 − 2 y ) + y + (1 − 2 y )( y ) = 5
2 2
K1
7y2 − 7y − 3 = 0
− (− 7 ) ± (− 7 )2 − 4(7 )(− 3)
y=
2(7 )
K1
y = 1.324 , − 0.324
N1
x = −1.648 , 1.648
N1
OR
1− x
y=
2
P1
1− x  1− x 
2x 2 +   + x =5
 2   2  K1
7 x 2 − 19 = 0
− (0 ) ± (0)2 − 4(7 )(− 19)
x=
2(7 )
K1
x = −1.648 , 1.648
N1
y = 1.324 , − 0.324
N1
5

2. 2 (a)
(
f ( x ) = − x 2 − 4 x − 21 )
K1
 −4 −4
2 2

= − x 2 − 4 x +   −  − 21

  2   2  

N1
= −( x − 2 ) + 25
2
(b) Max Value = 25 N1
(c) f (x )
25 (2,25)
21
x
-3 2 7
Shape graph N1
Max point N1
f ( x ) intercept or point (0,21) N1
d) f ( x ) = ( x − 2 ) − 25 N1
2
7
3 1 1
a) List of Areas ; xy, xy, xy K1
4 16
1
T2 ÷ T1 = T3 ÷ T2 =
4
1
This is Geometric Progression and r = N1
4
n −1
1 25
b) 12800 ×   =
4 512

3. n −1 K1
1 1
  =
4 262144
n −1 9
1 1
  = 
4 4
n −1 = 9 K1
n = 10
12800 N1
(c) S∞ =
1
1−
4 K1
2 N1
= 17066 cm 2
3
7
4 a)
4 cos 2 − 1 − 1 K1
4 cos 2 − 2
(
2 2 cos 2 − 1 ) N1
2 cos 2θ
b) i)
2
1
π 2π
-1
-2
P1
- shape of cos graph P1
- amplitude (max = 2 and min = -2) P1
- 2 periodic/cycle in 0 ≤ θ ≤ 2π
θ
b) ii) y = 1 − (equation of straight line) K1
π
Number of solution = 4 (without any mistake done) N1
7

4. 5 a)
Score 0–9 10 – 19 20 – 29 30 – 39 40 – 49
Number 3 4 9 9 10 N1
1 
 (35) − 7  P1
b) Q1 = 19.5 +  4 10
 9 
  K1
 
= 21.44
3 
 (35) − 25 
Q3 = 39.5 +  4 10 K1
 10 
 
 
= 40.75
Interquatile range K1
= 40.75 − 21.44
= 19.31 N1
6
6 (a) OQ = OA + AQ K1
OQ = (1 − m ) a + m b N1
~ ~
(b) (
PO + OQ = n PO + OR ) K1
OQ = (1 − n ) a + 3n b
4 N1
5 ~ ~
(c)
4 4  K1
(i)  − n  = 1 − m or 3n = m
5 5 
3 1
m= ,n= N1
11 11 N1
8 3
(ii) OQ = a+ b N1
11 ~ 11 ~
8

5. 2
7
= ∫ ( 2 y − y )dy
2
(a)(i) Area K1
0
2
 y3 
=  y2 − 
 3 0
4 N1
= unit 2
3
1 2
(ii) Area region P = ∫ y dy + ∫ ( 2 y − y )dy
2
K1
0 1
2
1   y3 
=  × 1× 1 +  y 2 −  K1
2   3 1
7 N1
= unit 2
6
4 7 1
(b) Area region Q = − = unit 2
3 6 6 K1
7 1
= :
6 6
=7:1 N1
1
(c) Volume π ∫ ( 2 y − y 2 ) dy
2
=
0 K1
1
 4 y3 y5 
= π − y4 +  K1
 3 5 0
8
= π unit 3 N1
15
10
8 (a) x 0.000 0.7071 1.000 1.414 1.732 N1
log10 y 1.000 1.330 1.477 1.672 1.826 N1
Using the correct, uniform scale and axes P1
All points plotted correctly P1
Line of best fit P1
1 P1
=
(b) log10 y x log10 p + log10 k
3

6. (i) use ∗ c = 10 k
log K1
k = 10.0 N1
1.83 − 1.0 1
(ii) =
use * m = 0.47977= log10 p K1
1.73 − 0 3
N1
p = 27.5
10
9
1  K1
2 π
(a) ∠COD = 
6 
1 N1
= π
= 1.047 rad
3
 1  20 K1
(b) (i) Arc ABC =  π − π  or = π
10
 3  3
1 
Length=
AC 202 − 102 or 20 cos  π rad  K1
6 
20 1
Perimeter = + 20 cos π = cm
π 38.267 N1
3 6
=
(ii) Area of shaded region
1
2
( ) 2
3
2 
102  π − sin π 
3 
K1
= 61.432cm2
N1
1
(c) ∠CDE = =
∠CAD π rad ( alternate segments ) K1
6
Area =
1
2
( ) 1 
102  π 
6 
K1
N1
= 26.183cm2
10

7. 10 (a) T ( 4, 2 ) P1
6+ x 6+ y
= 4, =2 K1
2 2
S ( 2, −2 ) N1
(b) y − 2 2 ( x − 4 )
= K1 K1
= 2x − 6
y N1
3 x + 24 3 y + 24 K1
(c) = 2 or = −2
7 7
 10 38  N1
U − ,− 
 3 3 
K1
(d) ( x − 2) + ( y + 2) = 2
2 2
( x − 4) + ( y − 2)
2 2
N1
3 x 2 + 3 y 2 − 28 x − 20 y + 72 =
0
10
11 (a) (i) P ( X 0=
= ) C0 (0.6)0 (0.4)10 or P ( X 1=
10
= ) 10
C1 (0.6)1 (0.4)9 K1
P ( X ≥ 2) = − [ P ( X = + P( X = ]
1 0) 1)
= 1 ─ 10C0 (0.6)0 (0.4)10 ─ 10C1 (0.6)1 (0.4)9 K1
= 0.9983 N1
2
(ii) 800 × K1
5
N1
= 320
(b)(i) P ( −0.417 ≤ z ≤ 1.25 ) K1
= 1 − 0.3383 − 0.1057
= 0.556 N1
(ii) P ( X > t ) =0.7977
Z = −0.833 P1
t − 4.5
−0.833 = K1
1.2
t = 3.5004
N1
10

8. Sub Total
No Mark Scheme
Marks Mark
1
12a i) (14) (5) sin θ = 21 K1 3
2
θ = ° or 36° 52 '
36.87
∠ BAC 180° − 36.87°
= K1
= ° or 143° 8'
143.13
N1
ii) BC 2 = 142 + 52 − 2(14)(5) cos 143.13° K1 2
BC 2 = 333
BC = 18.25 cm N1
iii) sin θ sin 143.13°
= K1 2
5 18.25
θ = ° or 9° 28'
9.46 N1
b i) A'
14 cm N1 1
5 cm
B' C'
ii) ∠ ACB 180° − 143.13° − 9.46°
= K1 2
= 27.41°
∠ A ' C ' B ' 180° − 27.41°
=
= ° or 152° 35'
152.59 N1 10

9. Sub Total
No Mark Scheme
Marks Mark
13 a) 4.55 n 3
=
m × 100 or × 100 =
112 K1
3.50 4
m = 130 n = RM 4.48 N1 N1
b) 110(70) + * 130( x) + 120( x + 1) + 112(2) K1 2
= 116.5
7 + x + x +1+ 2
x=3 N1
c i) See 140 P1 3
x (116.5)
= 140 K1
100
x = 120.17 / 120.2 N1
ii) x
× 100 =
140 K1 2
25
x = RM 35 N1 10

10. Sub Total
No Mark Scheme
Marks Mark
15 a) v 0 = − 30 ms −1 N1 1
b) − 3t 2 + 21t − 30 > 0 K1 2
( t − 5)( t − 2 ) < 0
2<t<5 N1
c) a = 6t + 21
− K1 3
a 5 = + 21
− 6(5) K1
a 5 = − 9 ms − 2 N1
d) − 3t 3 21t 2 K1 4
S = + − 30t
3 2
21t 2
S =t +
− 3
− 30t
2
21(3) 2
S3 = 3 +
− (3) − 30(3) =
− 22.5 or K1
2
21(5) 2
S5 = +
− (5) 3
− 30(5) =
−12.5
2
Total distance = − 22.5 + (− 22.5) − (−12.5) K1
= 32.5 m N1 10

11. Answer for question 14
(a) I. x + y ≤ 70 N1
y II. x ≤ 2y N1
III. y − 2 x ≤ 10 N1
(b) Refer to the graph,
K1
1 graph correct
3 graphs correct N1
90 Correct area
N1
(c) i) 15 ≤ y ≤ 40 N1
80 ii) k = 10x + 20y
max point ( 20,50 ) N1
70 Max fees = 10(20) + 20(50) K1
(20,50) = RM 1,200 N1
10
60
50
40
30
20
10
x
0 10 20 30 40 50 60 70 80

12. log10 y Answer for question 8
2.0
1.9
X
1.8
1.7
X
1.6
1.5
X
1.4
X
1.3
1.2
1.1
1.0 X
x
0 0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6 1.8