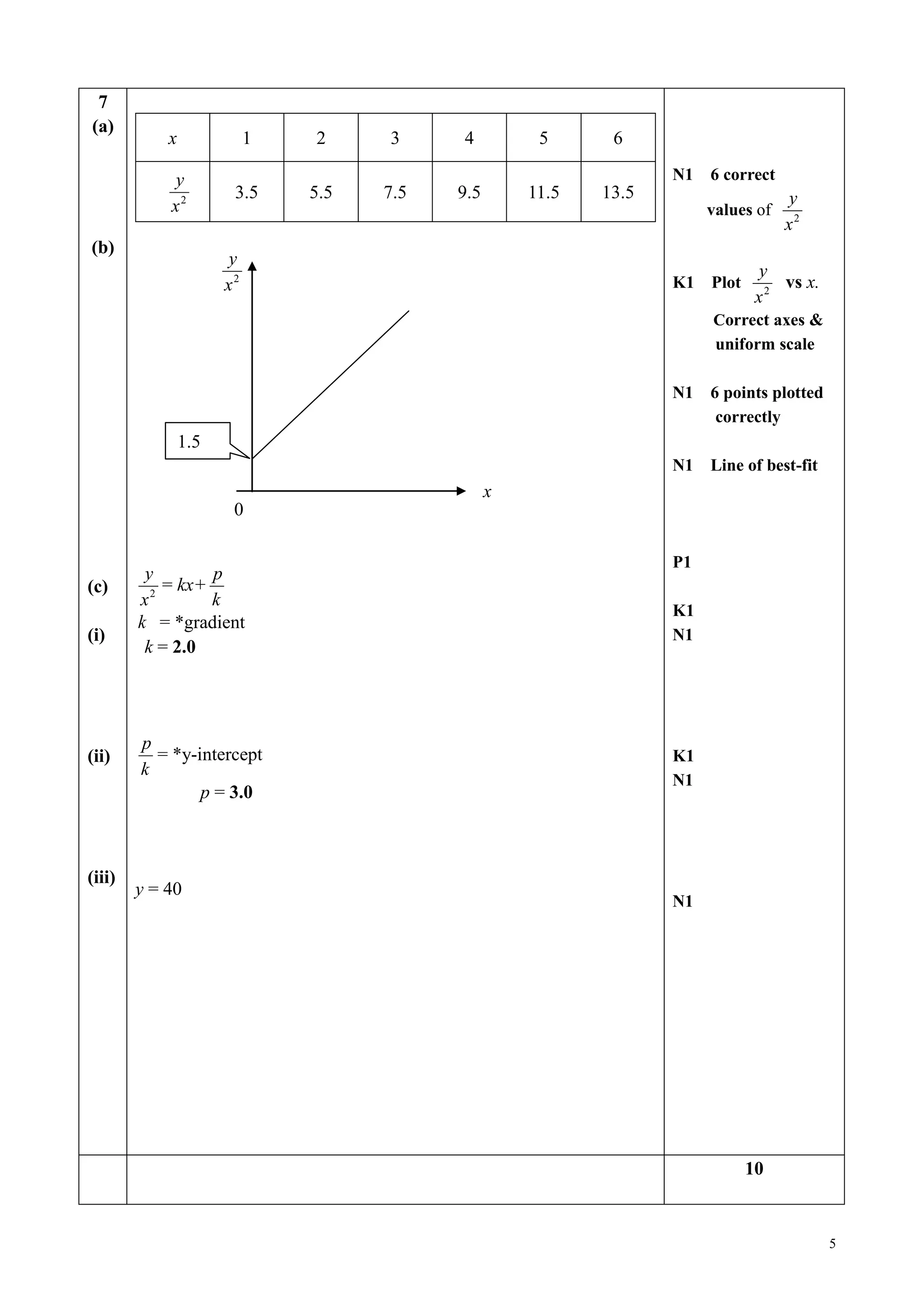
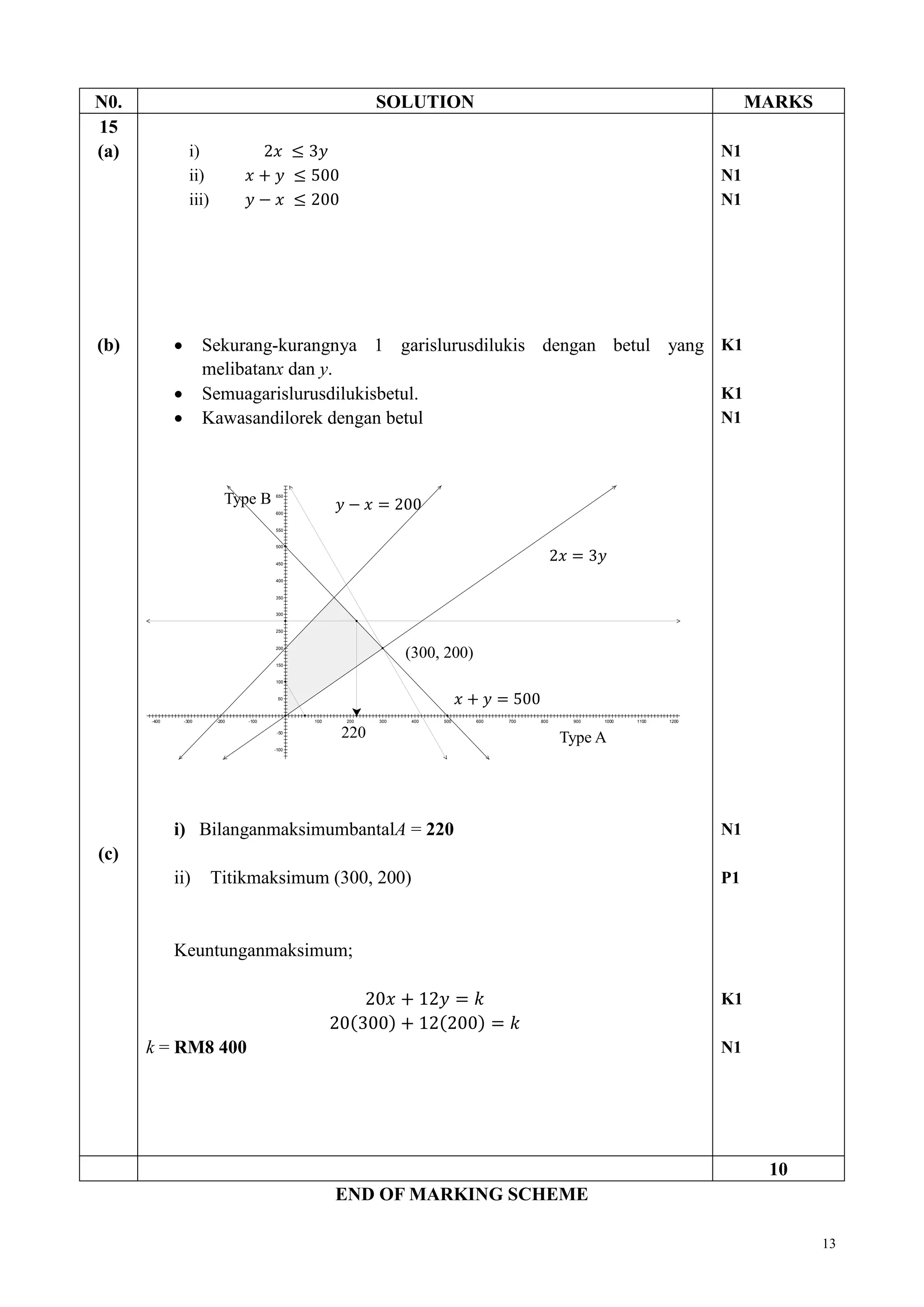
This document is a marking scheme for an Additional Mathematics exam paper. It provides the solutions to questions 1 through 15 on the paper and assigns marks to each part of each question's solution. For multiple part questions, each part is assigned marks. The highest number of marks given for a single part is 7. Overall, this marking scheme evaluates students' work on an Additional Mathematics exam and is used to determine marks and grades for their performance.

1. 1
Nama Pelajar : …………………………………
Tingkatan 5 : …………………….
3472/2
Additional Mathematics
August 2014
MODUL PENINGKATAN PRESTASI TINGKATAN 5
TAHUN 2014
ADDITIONAL MATHEMATICS
Paper 2
( MODUL 2 )
MARKING SCHEME

2. 2
SULIT 3472/2
MARKING SCHEME
ADDITIONAL MATHEMATICS PAPER 2 2014
N0. SOLUTION MARKS
1
x  2y 1 or
1
2
x
y


2 2 x  x  50
2 x  25
x  5 x  5
x  5 and x  5 (both)
y  2 and y  3 (both)
P1
K1 Eliminate x/y
K1 Solve quadratic equation
N1
N1
5
2
(a)
(b)
(i)
(ii)
7
8 (1)(2)
128
T 

10
10
(1)(2 1)
2 1
1023
1023 (3)(7)(5)
107415
S
V




 

1023 0.8
818.4


K1
N1
K1
K1
N1
K1
N1
7
3
(a)
(b)
y =
x

draw the straight line y =
x

Number of solutions = 3
P1 cos shape correct.
P1 Amplitude = 2 [ Maximum = 1
and Minimum = -1 ]
P1
1
1
2
cycle in 0  x   or
N1 For equation
K1 Sketch the straight line
N1
6
-4


3. 3
4
(a)
(b)
10
10
100
x
x




2
2 2
2
4 10
10
1160
x
x
 



10 3
2
6.5
mean



or
2
4
2
2
4


 

K1
N1
K1
N1
K1
N1 N1
7
5
(a)
(b)
5 125
5
5
3
5 5
3
5
3
log log 1
log
log 1
3
log log 3
log 3
125
K V
V
K
K V
K
V
K
V
 
 
 


i)
1( )
2
1 1
3
2 8 2
4 24
x k
f x
m
k
m m
m and k
 

  
  
ii)
1 1
( ) 3
8 2
20
p
p
 
 
K1
K1
N1
K1
K1
N1
K1
N1
8

4. 4
6
(a)
(b)
(3 1)(3 1)
( ) 3 1
3 1
'( ) 3
x x
f x x
x
f x
 
  


i)
2
2
3
2 (2) 3(2)
2
dy
kx x
dx
k
k
 
  
 
ii)
1
2
1
12 (2)
2
1
11
2
normal m
c
y x

 
 
K1
N1
K1
N1
P1
K1
N1
7

5. 5
7
(a)
(b)
(c)
(i)
(ii)
(iii)
x 1 2 3 4 5 6
2
y
x
3.5 5.5 7.5 9.5 11.5 13.5
2
y
x
2
y
x
= kx+
p
k
k = *gradient
k = 2.0
p
k
= *y-intercept
p = 3.0
y = 40
N1 6 correct
values of
2
y
x
K1 Plot
2
y
x
vs x.
Correct axes &
uniform scale
N1 6 points plotted
correctly
N1 Line of best-fit
P1
K1
N1
K1
N1
N1
10
1.5
0
x

6. 6
N0. SOLUTION MARKS
8(a)
i)
ii)
iii)
b)
2
(9 )
3
TS  x
2
PT
QR 
TR  TP  PQQR
PS  PT TS
MS  MR  RS
PS kMS
PS PT TS

 
6x 8y =
k =4
PS  4MS and S is a common point or equivalent
2 2
1 3
6( ) 8( )
2 4
PS
   
     
   
= 45
K1 (TS or QR )
N1
K1
N1
K1
N1
K1
N1
K1
N1
8 9 4
9 4
y x y
x y
   
 
 3 4 
2
9 4
3 4
2
3
2
2
TR
x y
x y
x y
x
y
   
  
    
 
 
 6x 8y
3
( 2 )
2
k x  y
= 6x
= 4y
 6x 8y

7. 7
9
a)
b)
c)
2
2
3 4
3 4 0
( 1)( 4) 0
4, 16
(4,16)
x x
x x
x x
x y
K
 
  
  
 
4
2
y
x


2
2
0
2
3
0
3
2
(4)(2)
8
3
2
8
3
16
3
x dx
x
cm
 
 
  
 
 
  
 


16
2
4
16
2
4
2 2
1
(4) (12)
3
64
2
16 4
64
2 2
256 16
64
2 2
56
ydy
y
 
 
 
 

 
  
 
 
   
 
 
    
 
 
    
 


K1 for solving
quad.eqn.
N1
N1
K1 use area of
rectangle -  ( y) dx
K1 integrate
correctly
and Sub.
the limit
correctly
N1
K1
K1 correct limit
K1 integrate
correctly
N1
10
Area B
Volume A

8. 8
N0. SOLUTION MARKS
10
(a)
(b)
(c)
60o
1.047 rad
8(1.047) OB S  or 8(2.095) BC S  OR 8(3.142) AC S 
= 8.38 = 16.76 = 25.14
Perimeter = 8.38+16.76+8 or Perimeter = 25.14 + 8
= 33.14 = 33.14
Area of OAB = 2 1
(8) (1.047)
2
= 33.50 cm2
Area of triangle OAB = 2 1
(8) sin 60
2
= 27.71
Area of the shaded region = 33.50 – 27.71
= 5.79 cm2
P1
N1
K1 Use s  r
N1
K1
N1
K1 Use formula
1 2
2
A  r 
K1
K1
N1
10

9. 9
N0. SOLUTION MARKS
11
(a)
(i)
(ii)
(b)
(i)
(ii)
X= Students passed Mathematics
p = 0.85 , q = 1- 0.85 = 0.15 , n = 6
P(X =6) = 6 6 0
6 c (0.85) (0.15)
=0.3772
P (Y≥2) = 1 – P(Y=0) – P(Y = 1)
Or = P(Y  2)  P(Y  3) ......... P(Y  6)
= 1 - 6 1 5
1c (0.15) (0.85) - 6 0 6
0 c (0.15) (0.85)
=0.2235
μ= 52 , σ =10
P( 40 < X < 60 ) = P (
40 52
10

< Z <
60 52
10

)
= P( -1.2 < Z < 0.8)
= 0.6731
n = 0.6731 x 500
n = 337
P1
K1 Use P ( X=r ) =
r n r
r
n C p q 
N1
K1
N1
K1 Use Z =

X  
K1
N1
K1
N1
10

10. 10
N0. SOLUTION MARKS
12
(a)
(b)
(c)
(d)
a  k 6t
k 6(2.5)  0
k = 15
2 3 15
2
s  t t
2 3 15
0
2
t t 
t = 7.5 s
2 15t 3t  0
t = 5
Total distance
=
5 7
2 2
3 3
0 5
15 15
2 2
t t
t t
   
      
   
d = 62.5 + 38
= 100.5
K1
N1
K1
K1
N1
K1
N1
K1 (for
Integration;
either one
and
substitute
the limit
5 7
0 5
 or )
K1
(for use and
summation)
N1
10

11. 11
N0.
SOLUTION
MARKS
13
(a)
(b)
(i)
(ii)
(iii)
(i)
KI (PetuaKosinus)
N1
K1 (Petua Sinus)
N1
K1 (GunaPetua Sinus)
K1
N1
K1
K1
N1
10

12. 12
N0.
SOLUTION
MARKS
14
(a)
(b)
(c)
(i)
Lihat 45º
I2012/2010 =
= 124.64
I2014/2010 = 124.64
= 137.10
Q2014 =
= RM685.50
K1
N1
K1
N1
K1
K1
N1
K1
K1
N1
10
i)

13. 13
N0. SOLUTION MARKS
15
(a)
(b)
(c)
i)
ii)
iii)
 Sekurang-kurangnya 1 garislurusdilukis dengan betul yang
melibatanx dan y.
 Semuagarislurusdilukisbetul.
 Kawasandilorek dengan betul
i) BilanganmaksimumbantalA = 220
ii) Titikmaksimum (300, 200)
Keuntunganmaksimum;
k = RM8 400
N1
N1
N1
K1
K1
N1
N1
P1
K1
N1
10
END OF MARKING SCHEME
650
600
550
500
450
400
350
300
250
200
150
100
50
-50
-100
-400 -300 -200 -100 100 200 300 400 500 600 700 800 900 1000 1100 1200
220
(300, 200)
Type B
Type A