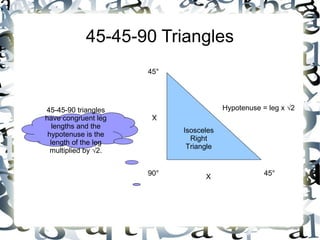
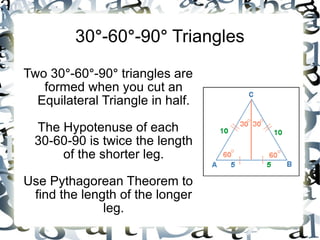
The document discusses different types of triangles and their angle and side properties: 1) It explains 45-45-90 triangles, also known as isosceles right triangles, have two equal leg lengths and a hypotenuse that is √2 times the length of either leg. 2) It discusses 30-60-90 triangles, which have angles of 30, 60, and 90 degrees. The hypotenuse of each triangle is twice the length of the shorter leg, and the longer leg is √3 times the length of the shorter leg. 3) Various properties of special right triangles like the Pythagorean theorem and multiplying square roots are presented to calculate side lengths from angles or other

1. Warm Up: Find the missing angle measurements Right Angle 18 ° Missing Angle Right Angle 54 ° Missing Angle The angles of ALL triangles add up to 180 degrees

2. Special Right Triangles Chapter 11 Section 5

3. Multiplying Square Roots For nonnegative numbers, the square root of a product equals the product of the square roots. This is how you determine answers not on page 746. √ 18 = √ 9 ∙ 2 = √9 ∙ √2 = 3 ∙ √2

4. 45 ° -45 ° -90 ° Triangles Isosceles Right Triangles also known as: 45 ° -45 ° -90 ° triangles. Use the degrees to identify these types of triangles.

5. How 45-45-90 Triangles Work C ² = A² + B² ← Pythagorean Theorem *Isosceles triangles have two equal length legs.* Therefore, A and B are the same length! C² = 2x² ← the length of the leg is now represented by x. C = √2x² ← Undo the square on the c. C = √2 ∙ √x² ← Multiplying Square Roots. C = √2 ∙ x ← The hypotenuse of a 45-45-90 triangle is always √ 2 multiplied by the length of the leg.

6. 45-45-90 Triangles Isosceles Right Triangle 90 ° 45 ° 45 ° X X Hypotenuse = leg x √2 45-45-90 triangles have congruent leg lengths and the hypotenuse is the length of the leg multiplied by √2.

7. What is the Square Root of 2? √ 2 = 1.41423562 So round answers to the nearest tenth unless asked to do otherwise.

8. 30 ° -60 ° -90 ° Triangles Two 30 ° -60 ° -90 ° triangles are formed when you cut an Equilateral Triangle in half. The Hypotenuse of each 30-60-90 is twice the length of the shorter leg. Use Pythagorean Theorem to find the length of the longer leg.

9. 30 ° -60 ° -90 °: Determine Long Leg C ² = A² + B² (2x)² = x² + B² ← B is the length of the long leg. 4x² = x² + B² 3x² = B² ← Minus x ² √ 3x² = B ← Undo square root √ 3 ∙ x = B ← Multiply square root The length of the longer leg = the √3 ∙ the length of the shorter leg.

10. Assignment #35: Handout

11. Cool Website On Triangles http://www.800score.com/content/guide7b2.html