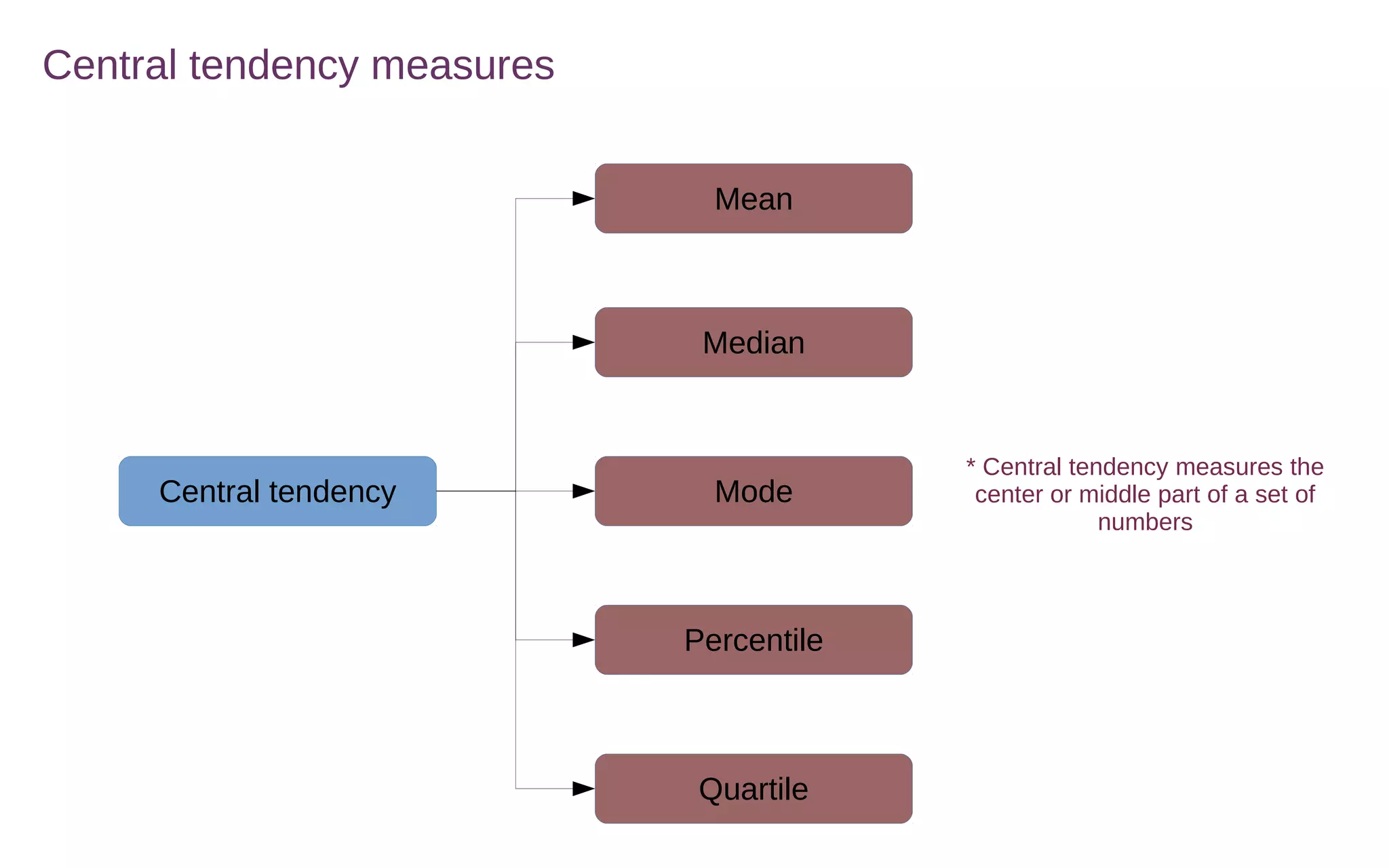
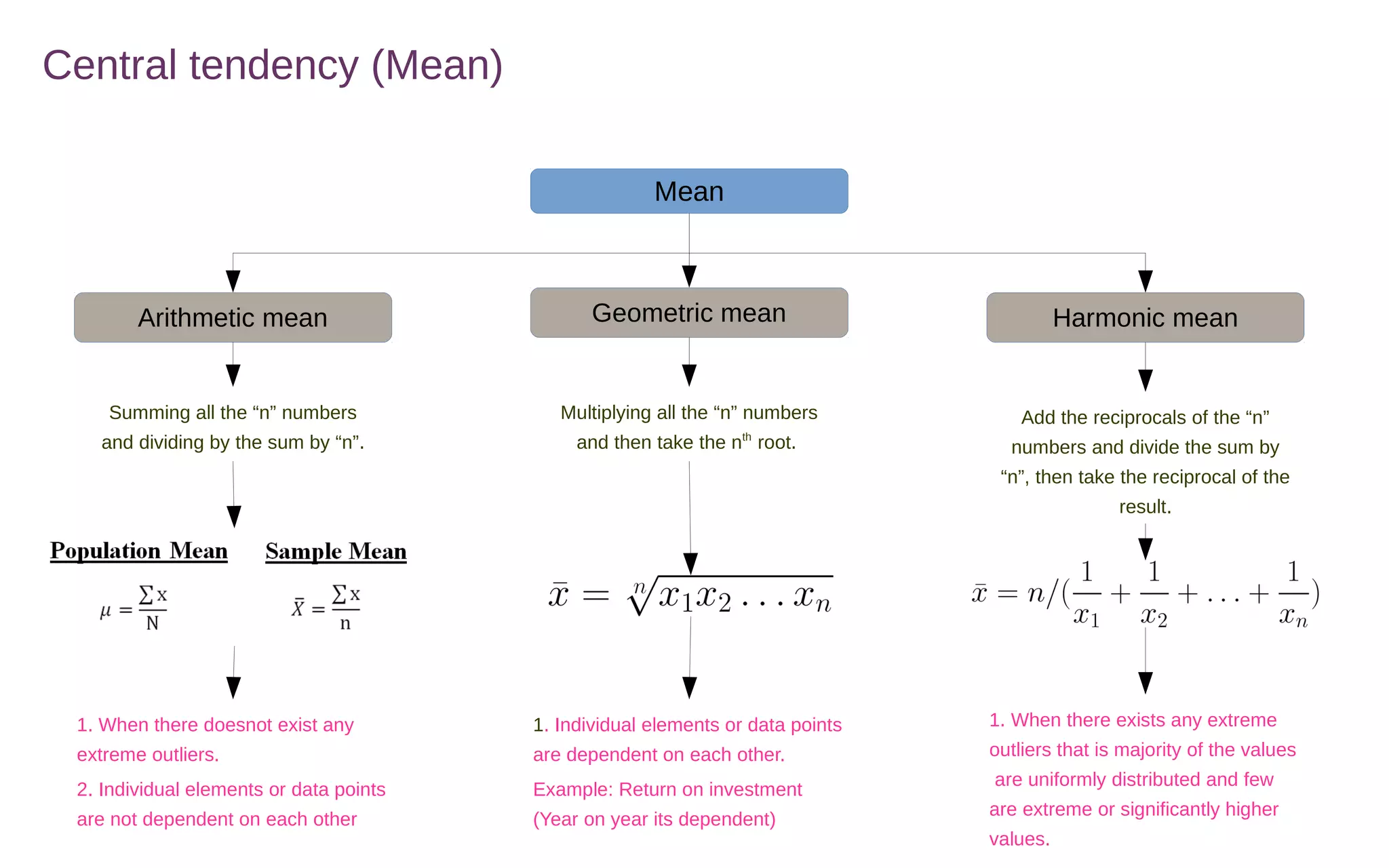
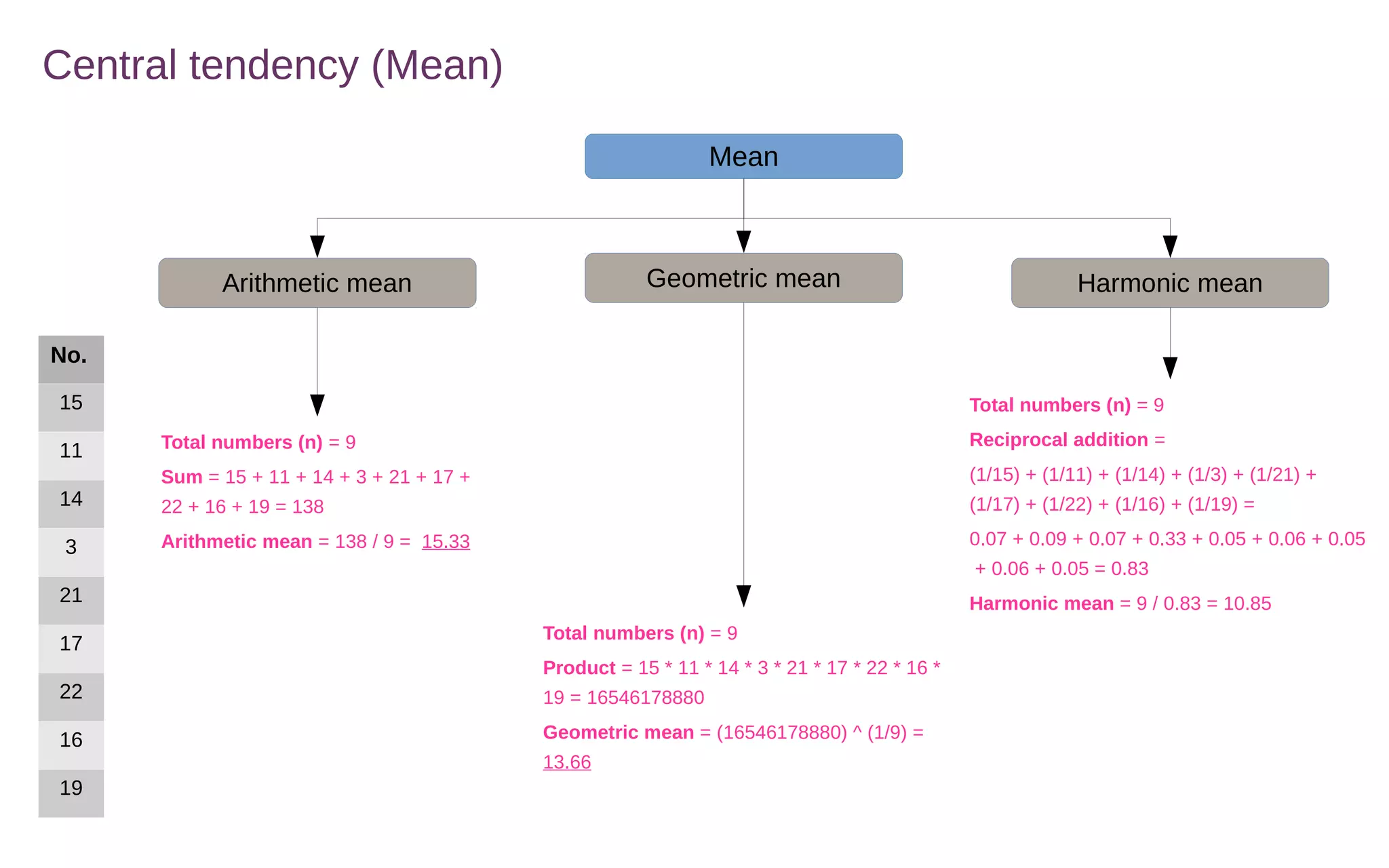
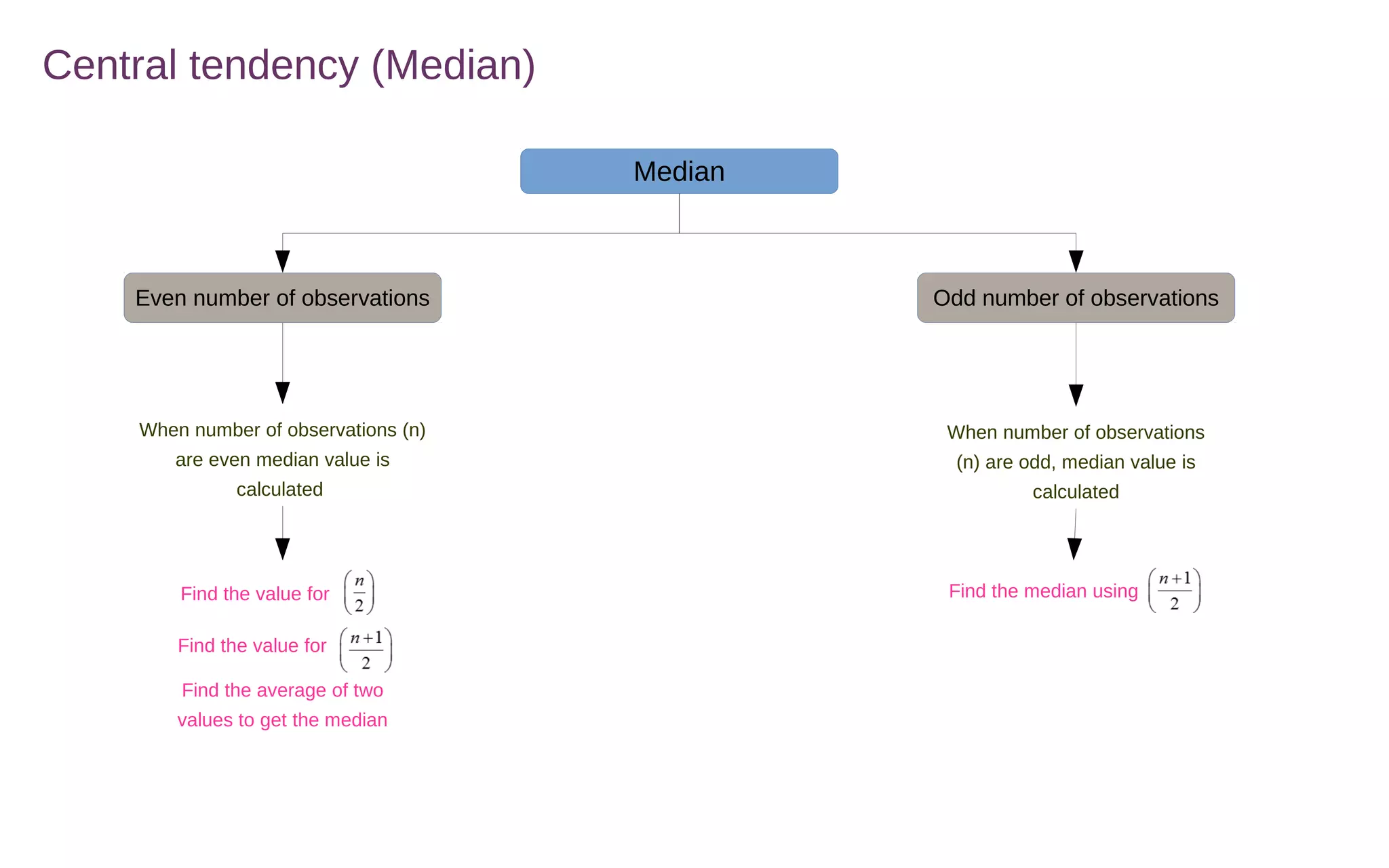
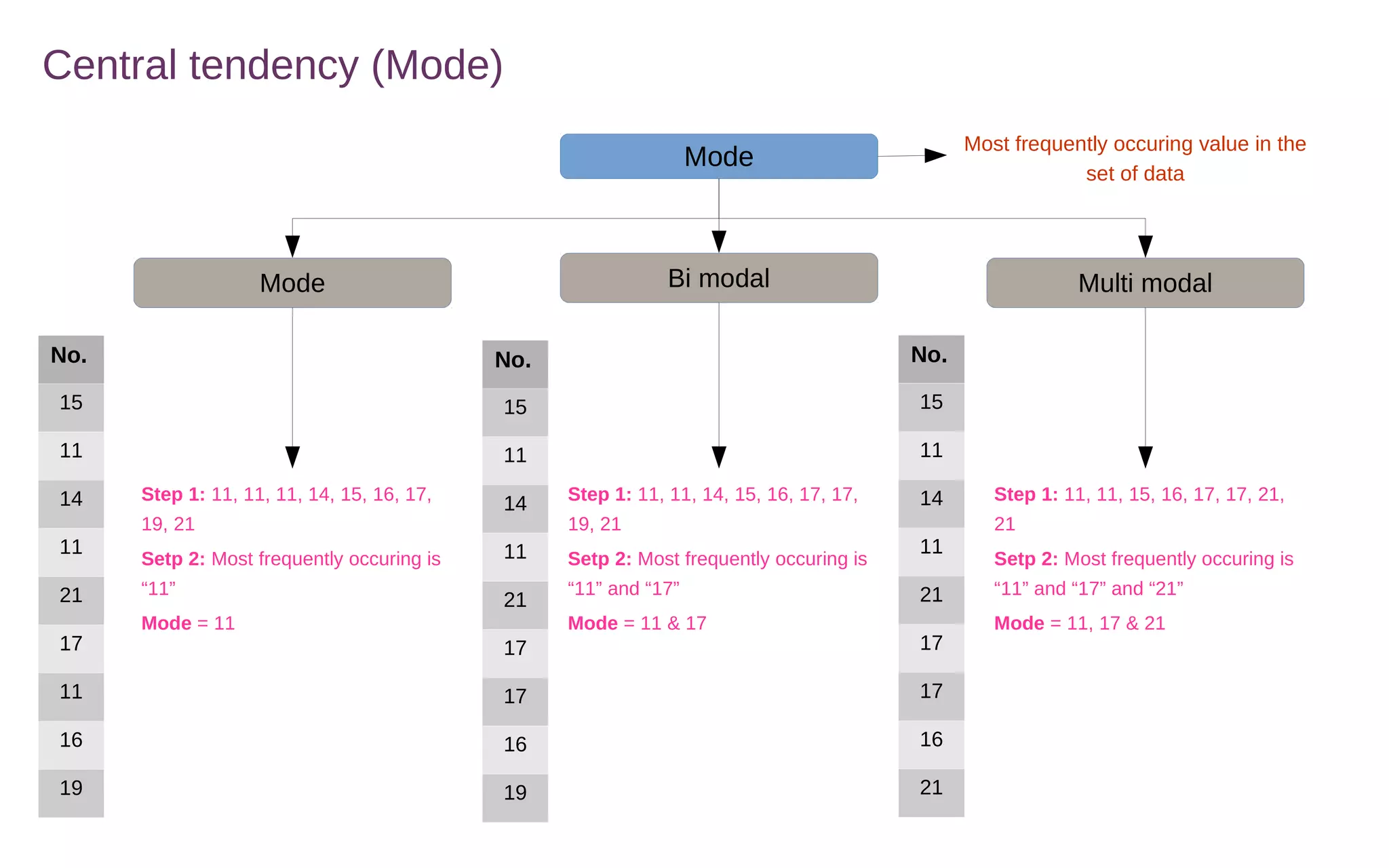
Central tendency measures describe the middle or center of a dataset. The three main measures are the mean, median, and mode. The mean is calculated by adding all values and dividing by the total number of values. The median is the middle value of a sorted list of values. The mode is the most frequently occurring value. Percentiles and quartiles divide a dataset into 100 and 4 equal parts, respectively. The 25th, 50th and 75th percentiles are called the first, second and third quartiles and describe the divisions of the data.

1. Descriptive statistics (Central tendency)

2. Central tendency measures
Central tendency
Mean
Median
Mode
Percentile
Quartile
* Central tendency measures the
center or middle part of a set of
numbers

3. Central tendency (Mean)
Mean
Harmonic meanGeometric meanArithmetic mean
Summing all the “n” numbers
and dividing by the sum by “n”.
Multiplying all the “n” numbers
and then take the nth
root.
Add the reciprocals of the “n”
numbers and divide the sum by
“n”, then take the reciprocal of the
result.
1. When there doesnot exist any
extreme outliers.
2. Individual elements or data points
are not dependent on each other
1. Individual elements or data points
are dependent on each other.
Example: Return on investment
(Year on year its dependent)
1. When there exists any extreme
outliers that is majority of the values
are uniformly distributed and few
are extreme or significantly higher
values.

4. Central tendency (Mean)
Mean
Harmonic meanGeometric meanArithmetic mean
No.
15
11
14
3
21
17
22
16
19
Total numbers (n) = 9
Sum = 15 + 11 + 14 + 3 + 21 + 17 +
22 + 16 + 19 = 138
Arithmetic mean = 138 / 9 = 15.33
Total numbers (n) = 9
Product = 15 * 11 * 14 * 3 * 21 * 17 * 22 * 16 *
19 = 16546178880
Geometric mean = (16546178880) ^ (1/9) =
13.66
Total numbers (n) = 9
Reciprocal addition =
(1/15) + (1/11) + (1/14) + (1/3) + (1/21) +
(1/17) + (1/22) + (1/16) + (1/19) =
0.07 + 0.09 + 0.07 + 0.33 + 0.05 + 0.06 + 0.05
+ 0.06 + 0.05 = 0.83
Harmonic mean = 9 / 0.83 = 10.85

5. Central tendency (Median)
Median
Odd number of observationsEven number of observations
When number of observations
(n) are odd, median value is
calculated
When number of observations (n)
are even median value is
calculated
Find the value for
Find the value for
Find the average of two
values to get the median
Find the median using

6. Central tendency (Median)
Median
Odd number of observationsEven number of observations
Step 1: Arrange the numbers in an ordered
array (Assecding or descending).
Step 2: For odd number of terms find the
middle term.
Step 3: For even number of terms find the
average of middle two terms.
* Median is the middle value in an ordered
array
No.
15
11
14
3
21
17
22
16
19
20
No.
15
11
14
3
21
17
22
16
19
Step 1: 3, 11, 14, 15, 16, 17, 19,
20, 21, 22
Setp 2: Even number of terms (10)
Median: (n/2) = (10/2) = 5
{(n+1)/2} = {(10+1)/2} = 5.5 (Round
= 6)
5th
term = 16 & 6th
term = 17
Median = (16+17) / 2 = 16.5
Step 1: 3, 11, 14, 15, 16, 17, 19, 21,
22
Setp 2: Odd number of terms (9)
Median: (n/2) = (9/2) = 4.5 (Round =
5)
5th
term = 16
Median = 5th
term = 16

7. Central tendency (Mode)
Mode
Multi modalBi modalMode
No.
15
11
14
11
21
17
11
16
19
Most frequently occuring value in the
set of data
Step 1: 11, 11, 11, 14, 15, 16, 17,
19, 21
Setp 2: Most frequently occuring is
“11”
Mode = 11
No.
15
11
14
11
21
17
17
16
19
No.
15
11
14
11
21
17
17
16
21
Step 1: 11, 11, 14, 15, 16, 17, 17,
19, 21
Setp 2: Most frequently occuring is
“11” and “17”
Mode = 11 & 17
Step 1: 11, 11, 15, 16, 17, 17, 21,
21
Setp 2: Most frequently occuring is
“11” and “17” and “21”
Mode = 11, 17 & 21

8. Central tendency (Percentiles)
* Divides the set of data into 100 parts
* There are 99 dividers to separate the set of data into 100 parts.
Example: 20th
percentile means 20% of the data are below the value and 80% of the data are above the value
Step 1: Order the set of numbers into ascending order
Step 2: Calculate the percentile location ( I )
I = (P / 100) * n
P -> Percentile of intrest
I -> Percentile (Data point location)
n -> Total number of data points
Step 3: Determine the location of data point
1. If “I” is a whole number, Pth
percentile is average of (Ith
location and (I + 1)th
location)
2. If “I” is not a whole number, Pth
percentile is (whole number partof “I” + 1)th
location
Example 1: 60th
percentile of 200 numbers
I = (60 / 100) * 200 = 0.6 * 200 = 120 (120 is a whole number, there by 60th
percentile will be the average of 120th
and
121th
number.
Example 2: 35th
percentile of 150 numbers
I = (35 / 100) * 150 = 0.35 * 150 = 52.5 (52.5 is not a whole number, there by whole number part is (52 +1) = 53. 53rd
term is the 35th
percentile

9. Central tendency (Quartiles)
* Divides the set of data into 4 parts.
* There are 3 dividers to separate the set of data into 4 parts.
Q1 = 25th
percentile
Q2 = 50th
percentile or median
Q3 = 75th
percentile
* Percentile formula can be used to calculate value at 25th
, 50th
, and 75th
percentile