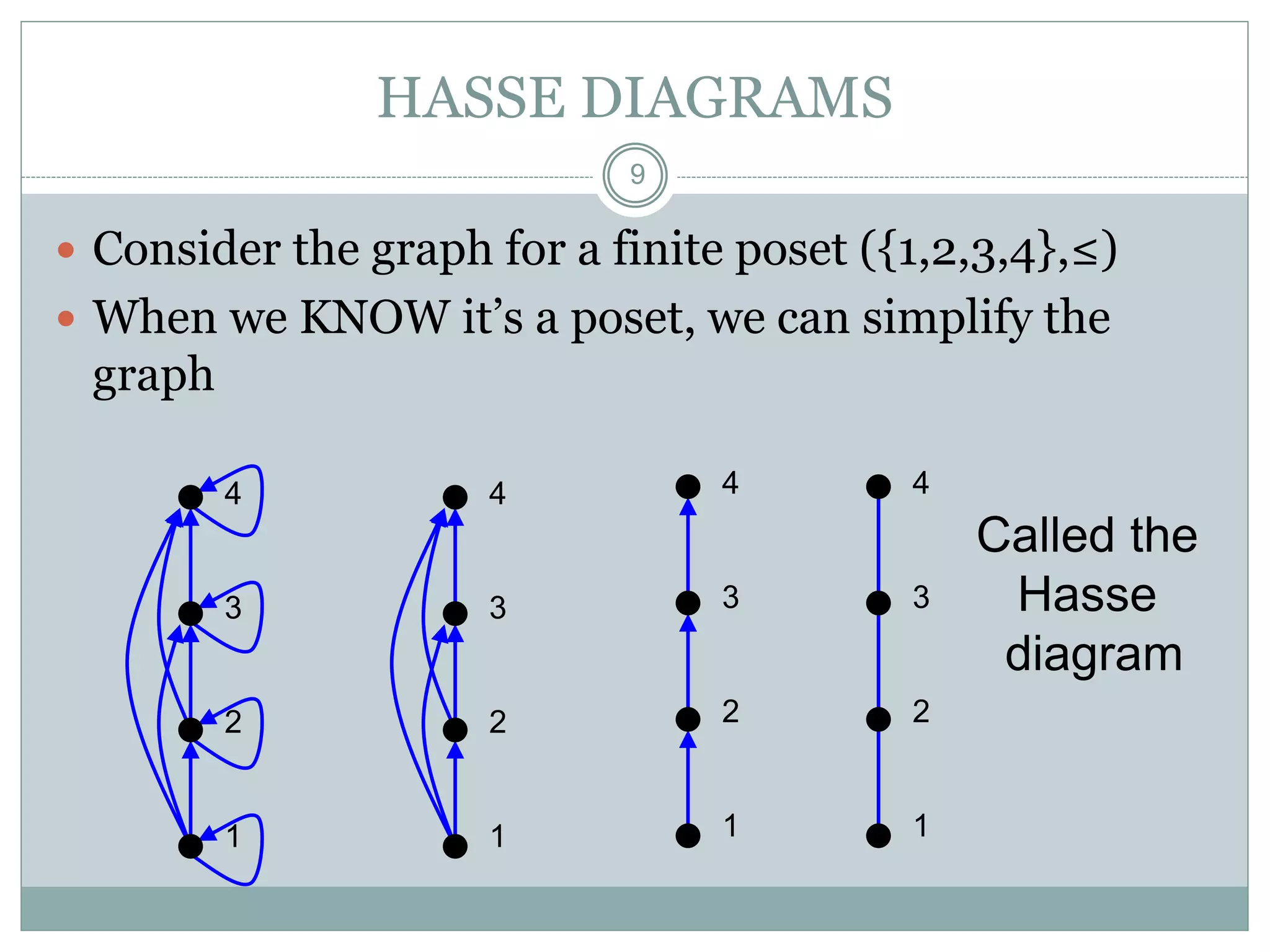
This document defines and provides examples of partial order relations. It discusses the key properties of a partial order being reflexive, antisymmetric, and transitive. Examples are given to show that the relation of greater than or equal to (≥) forms a partial order on integers, while division (|) forms a partial order on positive integers. The document also discusses comparability, total orders, well-ordered sets, and Hasse diagrams which are used to visually represent partial orders.

1. B Y
M E G H A J K U M A R M A L L I C K
M C A
1 S T Y E A R
1 S T S E M E S T E R
M C A / 2 5 0 1 7 / 1 8
1
PARTIAL ORDER RELATION

2. INTRODUCTION
2
 An equivalence relation is a relation that is reflexive,
symmetric, and transitive
 A partial ordering (or partial order) is a relation that is
reflexive, anti -symmetric, and transitive
 Recall that anti-symmetric means that if (a,b)  R, then (b,a) R
unless b = a
 Thus, (a,a) is allowed to be in R
 But since it’s reflexive, all possible (a,a) must be in R
 A set S with a partial ordering R is called a partially
ordered set, or poset
 Denoted by (S,R)

3. PARTIAL ORDERING EXAMPLES
3
 Show that ≥ is a partial order on the set of integers
 It is reflexive: a ≥ a for all a  Z
 It is antisymmetric: if a ≥ b then the only way that
b ≥ a is when b = a
 It is transitive: if a ≥ b and b ≥ c, then a ≥ c
 Note that ≥ is the partial ordering on the set of
integers
 (Z, ≥) is the partially ordered set, or poset

4. SYMBOL USAGE
4
 The symbol  is used to represent any relation
when discussing partial orders
 Not just the less than or equals to relation
 Can represent ≤, ≥,, etc
 Thus, a  b denotes that (a,b)  R
 The poset is (S,)
 The symbol  is used to denote a  b but a ≠ b
 If  represents ≥, then  represents >
 Fonts for this lecture set (specifically for the  and  symbols) are
available on the course website

5. COMPARABILITY
5
 The elements a and b of a poset (S,) are called
comparable if either a  b or b  a.
 Meaning if (a,b)  R or (b,a)  R
 It can’t be both because  is antisymmetric
 Unless a = b, of course
 If neither a  b nor b  a, then a and b are incomparable
 Meaning they are not related to each other
 This is definition 2 in the text
 If all elements in S are comparable, the relation is a
total ordering

6. COMPARABILITY EXAMPLES
6
 Let  be the “divides” operator |
 In the poset (Z+,|), are the integers 3 and 9
comparable?
 Yes, as 3 | 9
 Are 7 and 5 comparable?
 No, as 7 | 5 and 5 | 7
 Thus, as there are pairs of elements in Z+ that are not
comparable, the poset (Z+,|) is a partial order

7. COMPARABILITY EXAMPLES
7
 Let  be the less than or equals operator ≤
 In the poset (Z+,≤), are the integers 3 and 9
comparable?
 Yes, as 3 ≤ 9
 Are 7 and 5 comparable?
 Yes, as 5 ≤ 7
 As all pairs of elements in Z+ are comparable, the
poset (Z+,≤) is a total order
 a.k.a. totally ordered poset, linear order, chain, etc.

8. WELL-ORDERED SETS
8
 (S,) is a well-ordered set if:
 (S,) is a totally ordered poset
 Every non-empty subset of S has at least element
 Example: (Z,≤)
 Is a total ordered poset (every element is comparable to every other
element)
 It has no least element
 Thus, it is not a well-ordered set
 Example: (S,≤) where S = { 1, 2, 3, 4, 5 }
 Is a total ordered poset (every element is comparable to every other
element)
 Has a least element (1)
 Thus, it is a well-ordered set

9. HASSE DIAGRAMS
9
 Consider the graph for a finite poset ({1,2,3,4},≤)
 When we KNOW it’s a poset, we can simplify the
graph
4
3
2
1
4
3
2
1
4
3
2
1
4
3
2
1
Called the
Hasse
diagram

10. HASSE DIAGRAM
10
 For the poset ({1,2,3,4,6,8,12}, |)

11.  I T I S U S E D T O C A L C U L A T E T H E R A N K I N G O F
C O L L E G E S A C R O S S T H E W O R L D .
I T I S A L S O U S E D T O F I N D S C H E D U L E F O R V A R I O U S
S P O R T S .
11
REAL LIFE EXAMPLE

12. 12