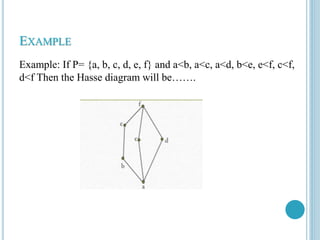
The document defines and provides examples of Hasse diagrams. It can be summarized as: Hasse diagrams are a type of mathematical diagram used to represent finite partially ordered sets. They involve drawing the elements of the set as vertices, and connecting vertices with line segments when one element covers another based on the ordering. Hasse diagrams uniquely determine the partial order and provide an intuitive visualization compared to listing out the ordering relationships. Examples are given of Hasse diagrams for power sets ordered by set inclusion and integer sets ordered by the divides relation.

1. HASSE DIAGRAM
MATHEMATICAL FOUNDATION OF COMPUTER SCIENCE
Nadar Saraswathi College Of Arts & Science - Theni
Nagapandiyammal N
M. Sc (CS)

2. HISTORY :
 Hasse diagrams are named after Helmut Hasse (1898–1979);
according to Garrett Birkhoff (1948), they are so called
because of the effective use Hasse made of them. However
Hasse was not the first to use these diagrams.
 One example that predates Hasse can be found in Henri
Gustav Vogt (1895). Although Hasse diagrams were originally
devised as a technique for making drawings of partially
ordered sets by hand, they have more recently been created
automatically using graph drawing techniques.
 The phrase "Hasse diagram" may also refer to the transitive
reduction as an abstract directed acyclic graph, independently
of any drawing of that graph, but this usage is eschewed here.

3. A "GOOD" HASSE DIAGRAM
 Although Hasse diagrams are simple as well as intuitive tools for
dealing with finite posets, it turns out to be rather difficult to draw
"good" diagrams. The reason is that there will in
 general be many possible ways to draw a Hasse diagram for a given
poset. The simple technique of just starting with the minimal
elements of an order and then drawing greater elements
 incrementally often produces quite poor results: symmetries and
internal structure of the order are easily lost.
 The following example demonstrates the issue. Consider the power
set of a 4-element set ordered by inclusion . Below are four different
Hasse diagrams for this partial order. Each
 subset has a node labelled with a binary encoding that shows
whether a certain element is in the subset (1) or not (0):

4. PARTIALLY ORDERED SETS
A partial order is a binary relation “≤” over a set P
which is reflexive, anti-symmetric, and transitive,
i.e., which satisfies for all a, b, and c in P
• a ≤ a (reflexivity);
• if a ≤ b and b ≤ a then a = b (anti-symmetry);
• if a ≤ b and b ≤ c then a ≤ c (transitivity). A set with a
partial order is called partially ordered set or poset.

5.  The power set of A = {a, b, c} consists of the family of
eight subsets: P(A): { , {a}, {b}, {c}, {a, b}, {a, c}, {b, c},
{a, b, c}} then, set inclusion relation “⊆ ” is a partial order
on P(A)
 Reflexive: Clearly any set in P(A) is a subset of itself.
Hence ⊆ is reflexive.
• Anti-symmetric: For any sets B and C in P(A) satisfying
B ⊆ C and C ⊆ B we have B = C. Hence ⊆ is anti-
symmetric.
• Transitive: For any three sets B, C and D in p(A) satisfying
B ⊆ C and C ⊆ D we have B ⊆ D. Hence ⊆ is transitive.
Hence ⊆ is a partial order on P(A).

6. HASSE DIAGRAM
 In order theory, a Hasse diagram is a type of
mathematical diagram used to represent a finite
partially ordered set, in the form of a drawing of its
transitive reduction.
 Concretely, for a partially ordered set (S, ≤) one
represents each element of S as a vertex in the plane and
draws a line segment or curve that goes upward from x
to y whenever y covers x (that is, whenever x < y and
there is no z such that
x < z < y).
 These curves may cross each other but must not touch
any vertices other than their endpoints. Such a diagram,
with labeled vertices, uniquely determines its partial
order.

7. EXAMPLE
Example: If P= {a, b, c, d, e, f} and a<b, a<c, a<d, b<e, e<f, c<f,
d<f Then the Hasse diagram will be…….

8.  Let A = {1, 2, 3, 9, 18} and consider the ‘divides’
relation A:
For all a, b ∈ A, a | b  b = ka for some integer k.
 The directed graph for the given relation is -> -> ->

9. LET’S CONSTRUCT A HASSE DIAGRAM………

10. THE END