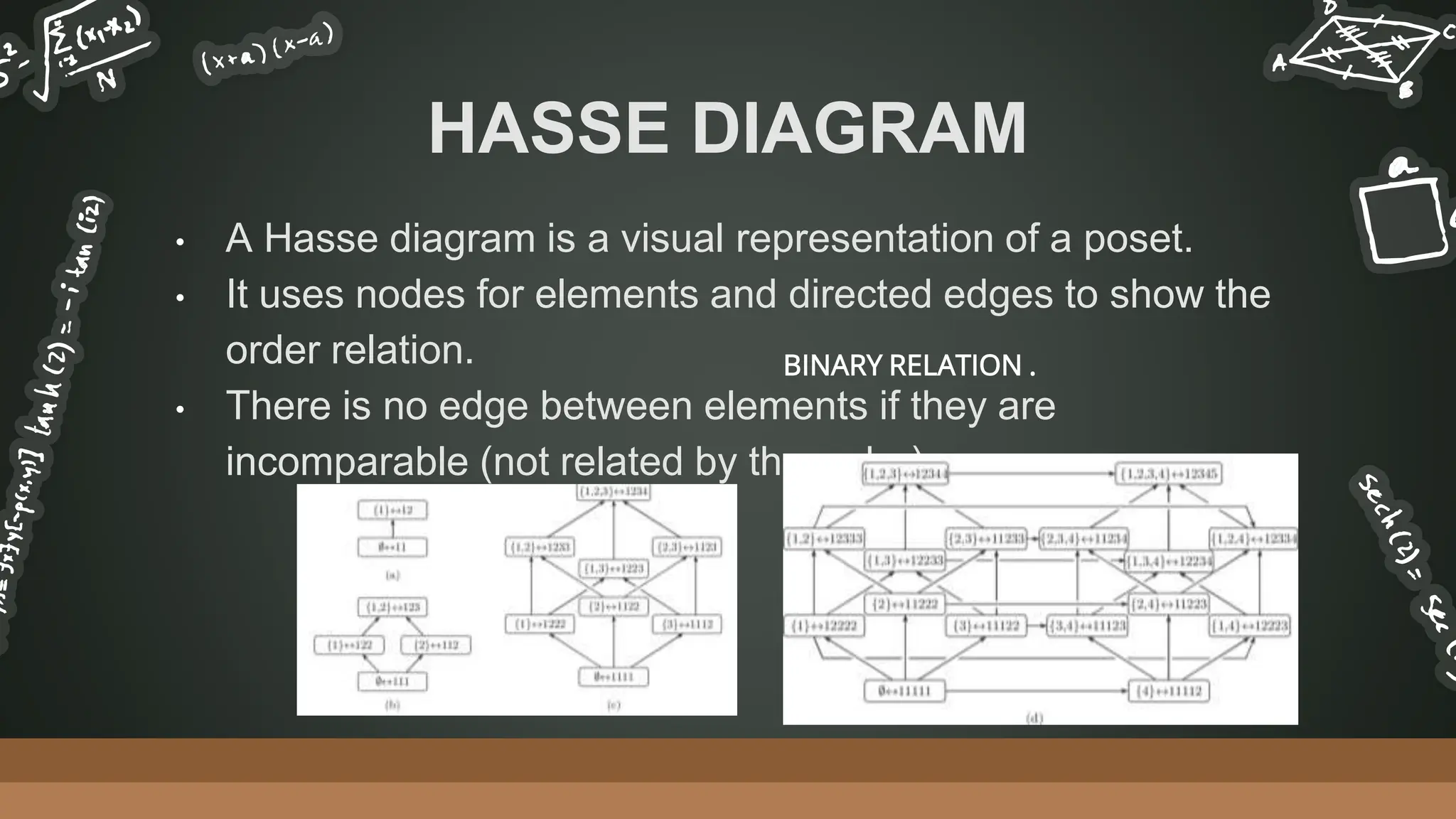
This document defines and explains different types of relations. It begins by defining a binary relation as a subset of the Cartesian product of two sets that specifies which ordered pairs are related. It then discusses various types of relations like reflexive, symmetric, transitive, and equivalence relations. The document also covers inverse relations, composite relations, equivalence classes, partitions of sets, partial order relations, partially ordered sets, and Hasse diagrams.

1. RELATION
AND ITS TYPE
RACHIT MEENA
BY-

2. 01
02
TOPICS
WHAT IS RELATION ?
BINARY RELATION .
03
04
05
06
07
08
INVERSE RELATION .
COMPOSITE RELATION .
TYPES OF RELATION.
EQUIVALENCE CLASS.
PROPERTIES OF EQUIVALENCE
CLASSES.
PARTITION OF A SET.
09 PARTIAL ORDER RELATION
10
PARTIALLY ORDERED SETS
(POSETS)
11 HASSE DIAGRAM

3. WHAT IS RELATION ?
Here's the basic idea:
Imagine you have a bunch of friends (set
A) and a group of movies (set B). A
relation in BCA math is like figuring out
who likes which movie. It's all about
connections between things!
‘A set of ordered pairs is defined as a
relation.’

4. BINARY RELATIONS
•A binary relation on two sets A and B
is a subset of the cartesian product A
x B.
•It specifies which ordered pairs (a, b)
are related, where a ∈ a and b ∈ b.

5. TYPES
Reflexive: Symmetric: Transitive:
Equivalence
:
Every element in A
is related to itself.
(a, a) ∈ R for all a ∈
A
A relation that is
reflexive,
symmetric, and
transitive.
If (a, b) ∈ R, then
(b, a) ∈ R.
If (a, b) ∈ R and (b,
c) ∈ R, then (a, c) ∈
R.
TYPES OF RELATIONS

6. • The inverse of a relation R on sets A and B,
denoted by R^-1, is a relation on B and A such
that (b, a) ∈ R^-1 if and only if (a, b) ∈ R.
• It reverses the order of the related elements.
INVERSE RELATION

7. • The composite relation of two
relations R on A x B and S on B x C,
denoted by S o R, is a relation on A
x C.
COMPOSITE RELATION

8. • An equivalence class of an equivalence relation
R on a set A is a collection of all elements in A
that are equivalent to each other under R.
• It groups elements based on the relation
EQUIVALENCE CLASSES

9. • Reflexive: Every element in A belongs to exactly
one equivalence class.
• Disjoint: No two equivalence classes have
common elements.
• Complete: The union of all equivalence classes
covers the entire set A.
PROPERTIES OF EQUIVALENCE
CLASSES

10. A partition of a set A is a collection of non-empty
subsets of A such that:
• The subsets are disjoint (no common
elements).
• The union of all subsets covers the entire set
A.
PARTITION OF A SET

11. A partial order relation (poset) on a set A is a binary relation ≤
that is:
• Reflexive: (a, a) ≤ a for all a ∈ A
• Antisymmetric: If (a, b) ≤ b and (b, a) ≤ a, then a = b.
• Transitive: If (a, b) ≤ b and (b, c) ≤ c, then (a, c) ≤ c.
PARTIAL ORDER RELATION

12. • A partially ordered set (poset) is a set A
equipped with a partial order relation ≤.
• We denote it as (A, ≤).
PARTIALLY ORDERED SETS
(POSETS)

13. • A Hasse diagram is a visual representation of a poset.
• It uses nodes for elements and directed edges to show the
order relation.
• There is no edge between elements if they are
incomparable (not related by the order).
HASSE DIAGRAM
BINARY RELATION .

14. CREDITS: This presentation template was created by Slidesgo, and includes icons
by Flaticon, and infographics & images by Freepik
Thanks!
BY-
Rachit Meena .
B.C.A 1ST YEAR .
Rachitmeena129@gmail.com