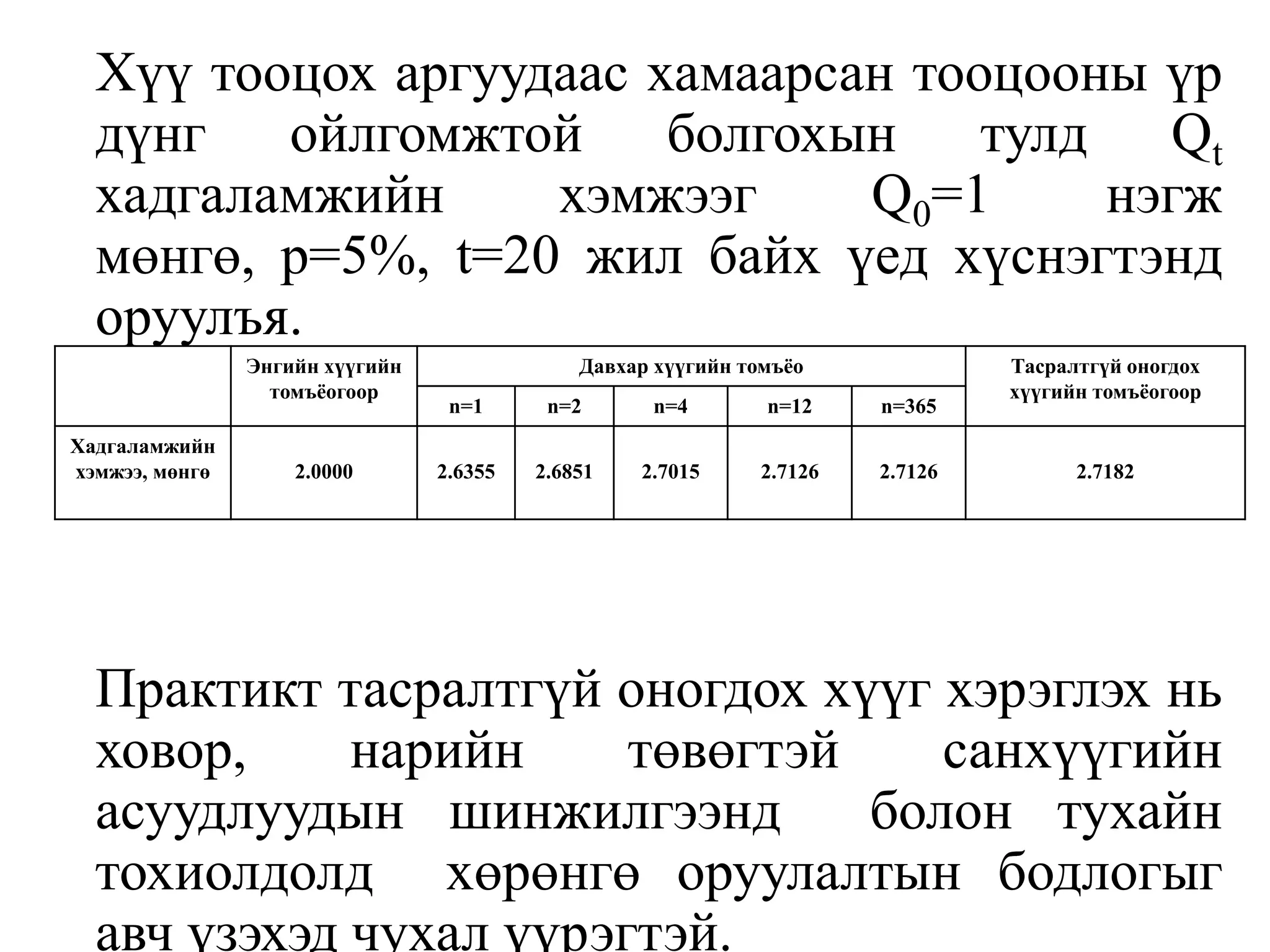
Документ обсуждает последовательности и пределы функций, включая определения и теоремы о предельных значениях и непрерывности. Рассматриваются примеры и теоремы, связанные с ограничениями и поведением функций при стремлении к определенным значениям. Упоминается также применение этих концепций в различных областях, таких как финансы и статистика.

1. Лекц №2Тоон дараалал ба функцийн хязгаар

2. Натурал тоо n бүхэнд хnтоо харгалзуулвалх1, х2,…,хп,...(1)гэсэн тоон олонлог үүснэ. Үүнийг тоон дараалал гэх ба хn-г дарааллын ерөнхий гишүүн гэнэ.Жишээ нь: 1,8,27,...,n3,... дарааллын ерөнхий гишүүн хn=n3 байна.

3. Тодорхойлолт: Дурын бага авахад гэсэн бүх дугааруудад тэнцэтгэл биш үргэлж биелэгдэж байх дугаар олдож байвал а тоог (1) дарааллын хязгаар гэж нэрлээдгэж тэмдэглэнэ.

4. (1) дарааллын хязгаар а байна гэдгийг уг дараалал а руу тэмүүлж байна гэх бөгөөд заримдаа үед гэж тэмдэглэдэг. Дарааллын хязгаар төгсгөлөг байвал түүнийг нийлдэг дараалал гэнэ. цэгийг агуулж байгаа дурын (а,b) завсрыгцэгийн орчин гэдэг.

5. Хэрэв (1) дараалал а гэсэн төгсгөлөг хязгаартай бол -ийн хувьд тэнцэл биш биелэгдэх ёстой. Эндээс буюу гэсэн тэнцэл биш гарна.

6. Тодорхойлолт: у =f(х) функц а цэгийн ямар нэг орчинд тодорхойлогдсон байг. Хэрвээ хичнээн ч бага байж болох тоо авахад (2) тэнцэтгэл бишийг хангасан бүх х-ийн хувьд (3)биелэгдэж байхаар тоо олдох бол А тоог f(х) функцийн үеийн хязгаар гэнэ.

7. Жишээ: у = 3х+1 функц үед 7 уруу тэмүүлнэ. Бодолт:

8. Зарим функцийн хувьд х нь а уруу нэг талаас нь тэмүүлэхэд нэг янз, нөгөө талаас нь тэмүүлэхэд өөр янзын хязгаартай байдаг. Иймд өрөөсгөл хязгаар гэдэг ойлголт орж ирдэг. Хэрэв у=f(х) функцийн х нь аруу зөвхөн баруун талаас нь тэмүүлэхэд b1гэсэн хязгаартай байвал түүнийг у=f(х) функцийн a цэг дээрхи баруун өрөөсгөл хязгаар гэж нэрлээдгэж тэмдэглэнэ.

9. Үүнтэй нэгэн адилаар зүүн өрөөсгөл хязгаар байна. Хэрэв у=f(х) функц үед төгсгөлөг A хязгаартай байвал байна. Үүний урвүу өгүүлбэр мөн хүчинтэй.

10. Тодорхойлолт: Тэг рүү тэмүүлдэг хувьсах хэмжигдэхүүнийг багасаж барагдашгүй хэмжигдэхүүн гэнэ. Хэрэв хувьсах хэмжигдэхүүн багасаж барагдашгүй бол

11. Багасаж барагдашгүй хэмжигдэхүүн ба хувьсах хэмжигдэхүүний хязгаарын хоорондын холбоог тогтоосон теоремыг авч үзье. Теорем:Хэрэв хувьсах хэмжигдэхүүн u ба тогтмол тоо а хоёрын ялгавар нь багасаж барагдашгүй хэмжигдэхүүн байвал а нь u-ийн хязгаар болох ба урвуугаар, хэрэв бол(4)байна. Энд а нь багасаж барагдашгүй хэмжигдэхүүн.

12. Багасаж барагдашгүй хэмжигдэхүүний зарим чанарыг дурдъя. 1. Төгсгөлөг тооны багасаж барагдашгүй хэмжигдэхүүний алгебрын нийлбэр багасаж барагдашгүй хэмжигдэхүүн байна.

13. 2. Дурын тооны багасаж барагдашгүй хэмжигдэхүүний үржвэр багасаж барагдашгүй хэмжигдэхүүн байна.Тодорхойлолт: Хувьсах хэмжигдэхүүн u-ийн бүх утгууд абсолют хэмжээгээрээ ямар нэг төгсгөлөг тоо М-ээс ихгүй бол u-г зааглагдсан хувьсах хэмжигдэхүүн гэнэ.

14. 3.Багасаж барагдашгүй хэмжигдэхүүнийг зааглагдсан хэмжигдэхүүнээр үржихэд багасаж барагдашгүй хэмжигдэхүүн гарна.Тодорхойлолт: Хязгааргүй уруу тэмүүлж байгаа хувьсах хэмжигдэхүүнийг ихсэж барагдашгүй хэмжигдэхүүн гэнэ.

15. 4. Хэрэв u ихсэж барагдашгүй хэмжигдэхүүн бол түүний урвуу хэмжигдэхүүн нь багасаж барагдашгүй хэмжигдэхүүн байна.

16. Хязгаарын тухай үндсэн теоремууд

17. Теорем: Хэрэв хувьсах хэмжигдэхүүн хязгаартай байвал тэр нь цор ганц байна.Теорем: Хувьсах хэмжигдэхүүн төгсгөлөг хязгаартай бол зааглагдсан байна.

18. Теорем: Тус бүрдээ төгсгөлөг хязгаартай тодорхой тооны функцүүдийн алгебрын нийлбэрийн хязгаар нэмэгдэхүүн тус , бүрийн хязгаарын алгебрын нийлбэртэй тэнцүү байна.

19. Теорем: Бүгдээрээ төгсгөлтэй хязгаартай төгсгөлөг тоон функцийн үржвэрийн хязгаар үржигдэхүүн тус бүрийн хязгаарын үржвэртэй тэнцэнэ.

20. Мөрдлөгөө: Тогтмол тоон үржигдэхүүнийг хязгаарын тэмдгийн өмнө гаргаж болно. Теорем: Хэрэв бол ноогдворын хязгаар хүртвэрийн хязгаарыг хуваарийн хязгаарт харьцуулсантай тэнцүү.

21. Ж:

22. Теорем: Хэрэв u, v, w хувьсах хэмжигдэхүүнүүдийн хувьд гэсэн тэнцэтгэл биш биелэгдэх бөгөөд u,vнь нэгэн ижил атоо руу тэмүүлж байвал wнь мөн а хязгаартай байна. Теорем: Монотон зааглагдсан хувьсах хэмжигдэхүүн хязгаартай байна.

23. Хязгаарын онолд 1 ба 2-р гайхамшигт хязгаар гэж нэрлэгддэг дараахь хоёр хязгаар чухал үүрэг гүйцэтгэдэг.

24. етоог бактерийн үржил, цацрагийн задрал, хүн амын өсөлт зэрэг процессуудад шинжилгээ хийх, статистик, физик, биологи, химийн болон бусад хэрэглээний олон бодлого бодоход хэрэглэдэг. Тасралтгүй оногдох хүүгийн бодлогыг авч үзье. Банкны хадгаламжинд анх Q0нэгж мөнгө хийв. Банк жил тутамд р%хүү төлдөг. T жилийн дараахи Qtхадгаламжийн хэмжээ олох шаардлагатай.

25. Энгийн хүүг ашиглах үед хадгаламжийн хэмжээ жил бүр адилхан хэмжээгээр өснө. Ө.х: Практикт ихэвчлэн давхар хүүгхэрэглэдэг. Хэрэв хадгаламжийн хүүг жилд нэг удаа бус харин n удаа бодвол жил бүр p%-иар өсөж байгаа учир жилийн хэсэгт -иар өснө. t жилийн хувьдntудаа өсөхөд хадгаламжийн хэмжээ болно. Хадгаламжийн хүүг сар болгон (n=12), улирал тутамд (n=4)…г.м (n->) бодож болно.

26. Хүү тооцох аргуудаас хамаарсан тооцооны үр дүнг ойлгомжтой болгохын тулд Qtхадгаламжийн хэмжээг Q0=1 нэгж мөнгө, p=5%, t=20 жил байх үед хүснэгтэнд оруулъя.Практикт тасралтгүй оногдох хүүг хэрэглэх нь ховор, нарийн төвөгтэй санхүүгийн асуудлуудын шинжилгээнд болон тухайн тохиолдолд хөрөнгө оруулалтын бодлогыг авч үзэхэд чухал үүрэгтэй.

27. Функцийн тасралтгүй чанар

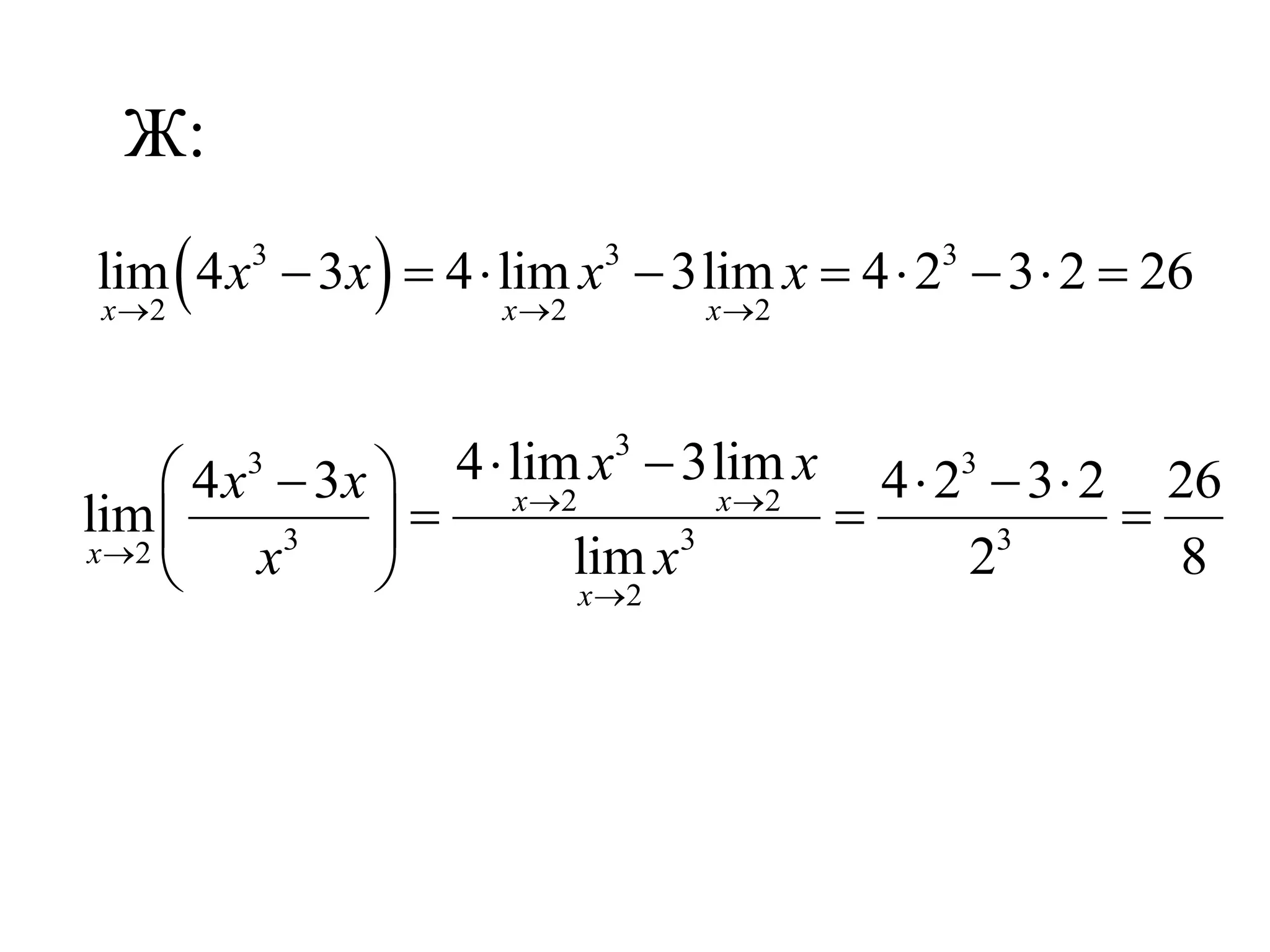
28. у=f(х) функц х = х0 цэг дээр ба түүний орчинд тодорхойлогдсон бөгөөд y0=f(x0) байг.[а,b] хэрчим дээр тодорхойлогдсон у=f(х) функц авч цэг дээр утгыг бодвол y0=f(x0) болох ба х0–д байхаар өөрчлөлт өгвөл функцийнн утга нь болно. Энэ үедялгаврыг у = f(x) функцын x0цэг дээрхи өөрчлөлт гэнэ.

29. Тодорхойлолт1: Хэрэв у = f(х) функц х = х0 цэг ба түүний орчинд тодорхойлогдож байвал у = f(х) функцыг х = х0 цэг дээр тасралтгүй функц гэнэ. Ө.х: аргументын багасаж барагдашгүй өөрчлөлтөнд функцын багасаж барагдашгүй өөрчлөлт харгалзаж байвал у = f(х) функцыг х = х0 цэг дээр тасралтгүй гэдэг.

30. Тодорхойлолт2: Хэрэв у = f(х) функцын х аргументх0уруутэмүүлэхэд байвал уул функцыг х = х0цэг дээр тасралтгүй гэнэ. Хэрэв нөхцөл биелэгдэж байвал f(х)-ыг х = х0цэг дээр баруун талаасаатасралтгүйбол зүүн талаасаа тасралтгүй функц гэнэ.

31. Тодорхойлолт3: Хэрэв у = f(х) функц ямар нэг (а,b) завсрын бүх цэгүүд дээр тасралтгүй бөгөөд х = а цэг дээр баруун талаасаа, х = b дээр зүүн талаасаа тасралтгүй байвал түүнийг [а,b] хэрчим дээр тасралтгүй гэдэг. Хэрэв х = х0 цэг дээр у = f(х) функцын тасралтгүй чанар алдагдаж байвал х0 цэгийг уг функцын тасралтын цэг гэнэ.

32. Теорем 1 Хэрэв [а,b] хэрчим дээр монотон у = f(х) функц утгуудын олонлог ямар нэг Ү завсрыг бүхэлд нь дүүргэж байвал у = f(х) нь [а,b] хэрчим дээр тасралтгүй байна. Энэ теоремыг ашиглан үндсэн элементар функцүүд тодорхойлогдох муж дээрээ тасралтгүй, мөн тасралтгүй функцүүд дээр үйлдэл хийхэд мөн тасралтгүй функц гарна.

33. Теорем 2: Хэрэв f(х), g(х) функцүүд х = х0 цэг дээр тасралтгүй болf(х) ± g(х), f(х) • g(х) ба хэрэв байвал функцүүд x =x0цэг дээр тасралтгүй байна.Теорем 3: Хэрэв функц х = х0 цэг дээр тасралтгүй u = f(у) функц дээр тасралтгүй байвал давхар функц х = х0 цэг дээр тасралтгүй байна,

34. Чанар1. Хэрэв (а,b) хэрчим дээр тодорхойлогдсон тасралтгүй y=f(x)функц хэрчмийн төгсгөлийн цэгүүд дээр эсрэг тэмдэгтэй утга авдаг бол f(с) = 0 байх х = с цэг [а,b] хэрчмээс ядаж нэг олдоно.Энэ чанарыг геометр утга нь тасралтгүй муруй Оx тэнхлэгийн нэг талаас нөгөөд гарахдаа түүнийг ядаж нэг удаа огтлоно. y a b x

35. Чанар2:Хэрэв[а,b]хэрчим дээр тодорхойлогдсон у = f(х) функц тасралтгүй бөгөөдбол А,В хоёрын хоорондох дурын с утгыг функц (а, b) хэрчмийн ямар нэг С цэг дээр заавал авна.Чанар3: Хэрэв у = f(х) функц [а, b] дээр тодорхойлогдсон бөгөөд тасралтгүй бол энэ хэрчим дээр зааглагдсан байна. Ө.хбайх m,М тоонууд олдоно.

36. Чанар4: Битүү завсар дээр тодорхойлогдсон бөгөөд тасралтгүй функц энэ завсар дээр хамгийн их ба бага утгаа заавал авна.

37. Багасаж барагдашгүй хэмжигдэхүүнийг жиших Багасаж барагдашгүй хэмжигдэхүүн α,β-г нэгэн ижил х аргументын функцүүд бөгөөд х->а үед тэг рүү тэмүүлдэг гэж үзье.Тодорхойлолт1: Хэрэв харьцаа тэгээс ялгаатай хязгаартай, өөрөөр хэлбэл: байвал тэдгээрийг ижил эрэмбийн багасаж барагдашгүй хэмжигдэхүүн гэнэ.

38. Жишээ1. α=sin x,β= 2х ба х->0 гэе.Бодолт. Тэгвэлболох тул sinx, 2x нь х->0 үед ижил эрэмбийн багасаж барагдашгүй хэмжигдэхүүн байна.

39. Тодорхойлолт 2: Хэрэв харьцаа тэг рүү тэмүүлж байвал, Ө.х бол β-г α-аас дээд эрэмбийн багасаж барагдашгүй хэмжигдэхүүн гэнэ. Хэрэв бол α-г β-тэй харьцуулахад к эрэмбийн багасаж барагдашгүй хэмжигдэхүүн гэнэ.

40. Тодорхойлолт 3: Хэрэв багасаж барагдашгүй хэмжигдэхүүн α,β хоёрын харьцааны хязгаар 1-тэй тэнцүү бол тэдгээрийг эн чацуу багасаж барагдашгүй хэмжигдэхүүн гэх бөгөөд α ~ β гэж тэмдэглэнэ.Теорем1 Хэрэв α,βхоёр эн чацуу багасаж барагдашгүй хэмжигдэхүүн бол α-β нь α-аас ч, β-аас ч дээд эрэмбийн багасаж барагдашгүй байна.

41. Хэрэв α ~ α1, β~β1 бабол байна. Өөрөөрхэлбэл багасаж барагдашгүй хэмжигдэхүүнүүдийн харьцааны хязгаар тэдгээрийг эн чацуу хэмжигдэхүүнээр солиход өөрчлөгдөхгүй.

42. Жишээ: хязгаарыг олъё. Бодолт. х->0 үедtg3x~3х, sin4х ~ 4хучирэнчацуу багасаж барагдашгүй хэмжигдэхүүнээр соливолболно.