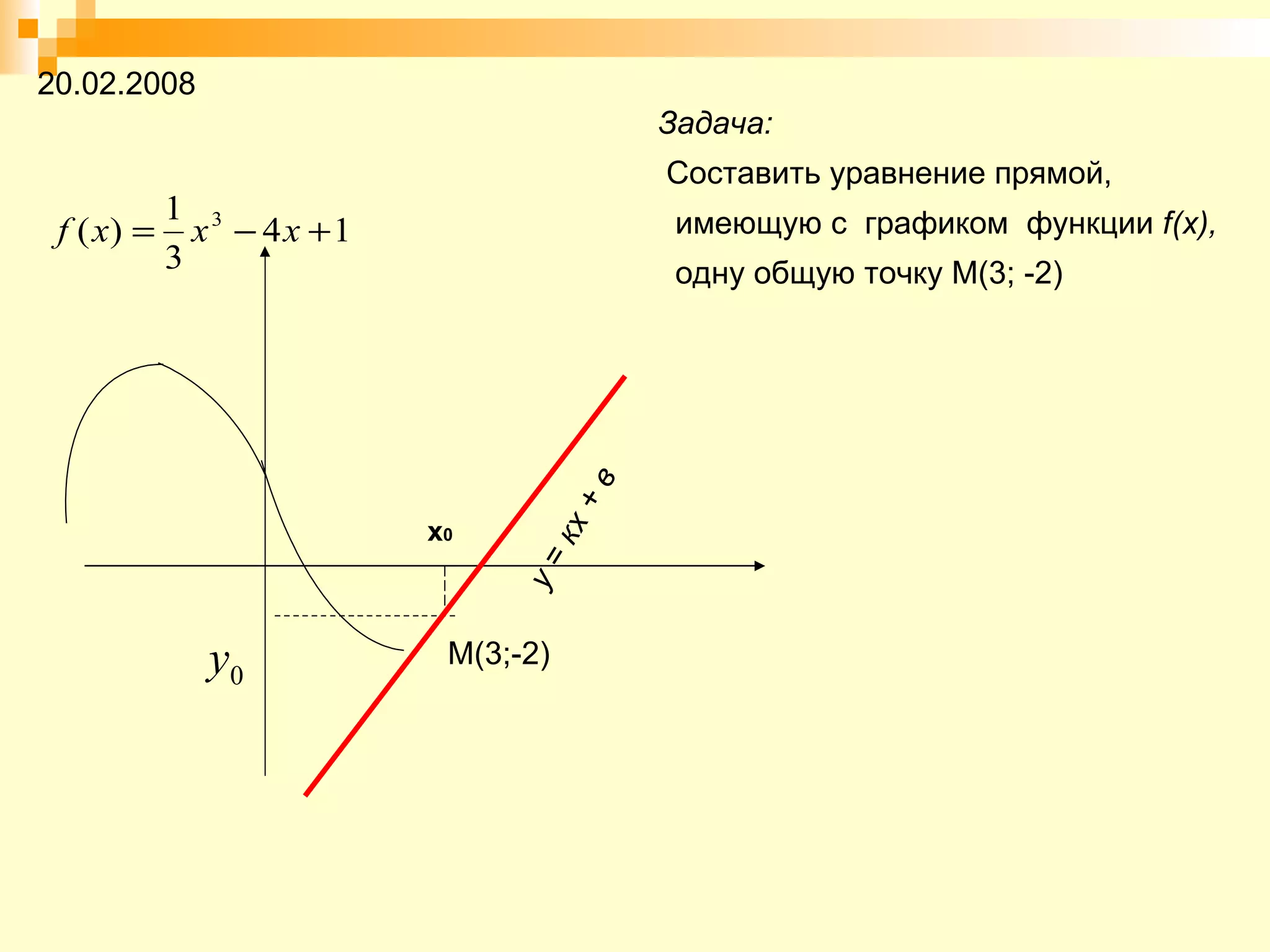
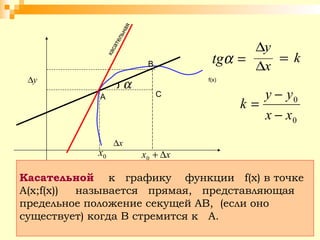
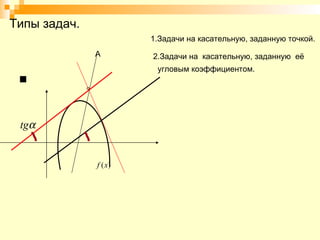
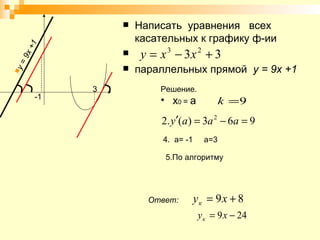
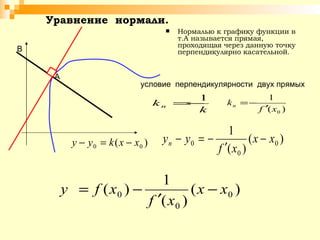
Документ описывает урок математики, посвященный составлению уравнений касательной и нормали к графику функции, с фокусом на геометрическом смысле производной. Рассматриваются алгоритмы решения задач и типы задач, включая то, как находить уравнения касательной и нормали в заданной точке. Также представлены задания на дом для практики изученного материала.

1. М(3;-2) х 0 у = кх + в Задача: Составить уравнение прямой, имеющую с графиком функции f(x) , одну общую точку М(3; -2) 20.02.2008

2. Уравнение касательной и нормали к графику функции. 10 класс Физико-математический профиль Учитель Ласкевич С.В.

3. Цель урока: 1)узнать как составлять уравнение касательной к графику 2)Подготовиться к самостоятельному распознаванию типа ключевых задач для решения задач, требующих исследовательских умений. 3)научиться решать задачи по теме. Девиз урока: «Решай, ищи, твори и мысли» Планируемый результат урока: Уметь составлять уравнение касательной и нормали к графику функции. Научиться распознавать опорные типы задач, для решения более сложных.

4. Касательной к графику функции f ( x ) в точке А(х; f (х)) называется прямая, представляющая предельное положение секущей АВ, (если оно существует) когда В стремится к А. f(x) A B С касательная

5. f(x) A B х 0 х 0 + х касательная Угловой коэффициент касательной получается из углового коэффициента секущей в процессе предельного перехода от В k А но условие В -> А можно заменить условием С

6. Значение производной функции y = f ( x ) в точке касания Х 0 равно угловому коэффициенту касательной к графику ф-ии y = f ( x ) в т Х 0 . - Геометрический смысл производной

7. Пусть в точке А проведена касательная Уравнение любой прямой проходящей через данную точку имеет вид Или

8. Решение исходной задачи. Решение. Алгоритм составления уравнения касательной: 1. 2. 3. 4. М (3,-2) Составьте уравнение касательной к графику функции в точке M(3; – 2).

9. Типы задач. 1.Задачи на касательную, заданную точкой. 2.Задачи на касательную, заданную её угловым коэффициентом. А

10. Если функция дифференцируема в т х=а то в этой точке к графику можно провести касательную и обратно: если в х=а к графику y = f ( x ) можно провести невертикальную касательную , то. функция дифференцируема в т х=а - Это позволяет по графику ф-ии находить точки в ко­торых ф-ия имеет или не имеет производную.

11. Написать уравнения всех касательных к графику ф-ии параллельных прямой у = 9х +1 -1 3 у = 9х +1 Решение. х 0 = а 4. а= -1 а=3 5.По алгоритму Ответ:

12. Уравнение нормали. Нормалью к графику функции в т.А называется прямая, проходящая через данную точку перпендикулярно касательной. А В условие перпендикулярности двух прямых

13. Решить самостоятельно. 1). Составить уравнение нормали к кривой в точке (2; 8). Ответ. 2 ) . При каком значении параметра « р» касательная к графику функции в точке (1;1) образует с осью ох угол равный Ответ:

14. Решение задач.(устно) Найти значение производной в точке х, если угловой коэффициент касательной к графику этой функции в т.х равен 0,18. Найти тангенс угла наклона к оси абсцисс касательной в точке (2;2) к графику функции

15. Итог урока. Что называется касательной к графику функции? Что называется нормалью к графику функции? Назвать алгоритм составления уравнения касательной и нормали. В чём состоит геометрический смысл производной?

16. Задание на дом. Ананченко К.О п.70 № 465 Всем спасибо.