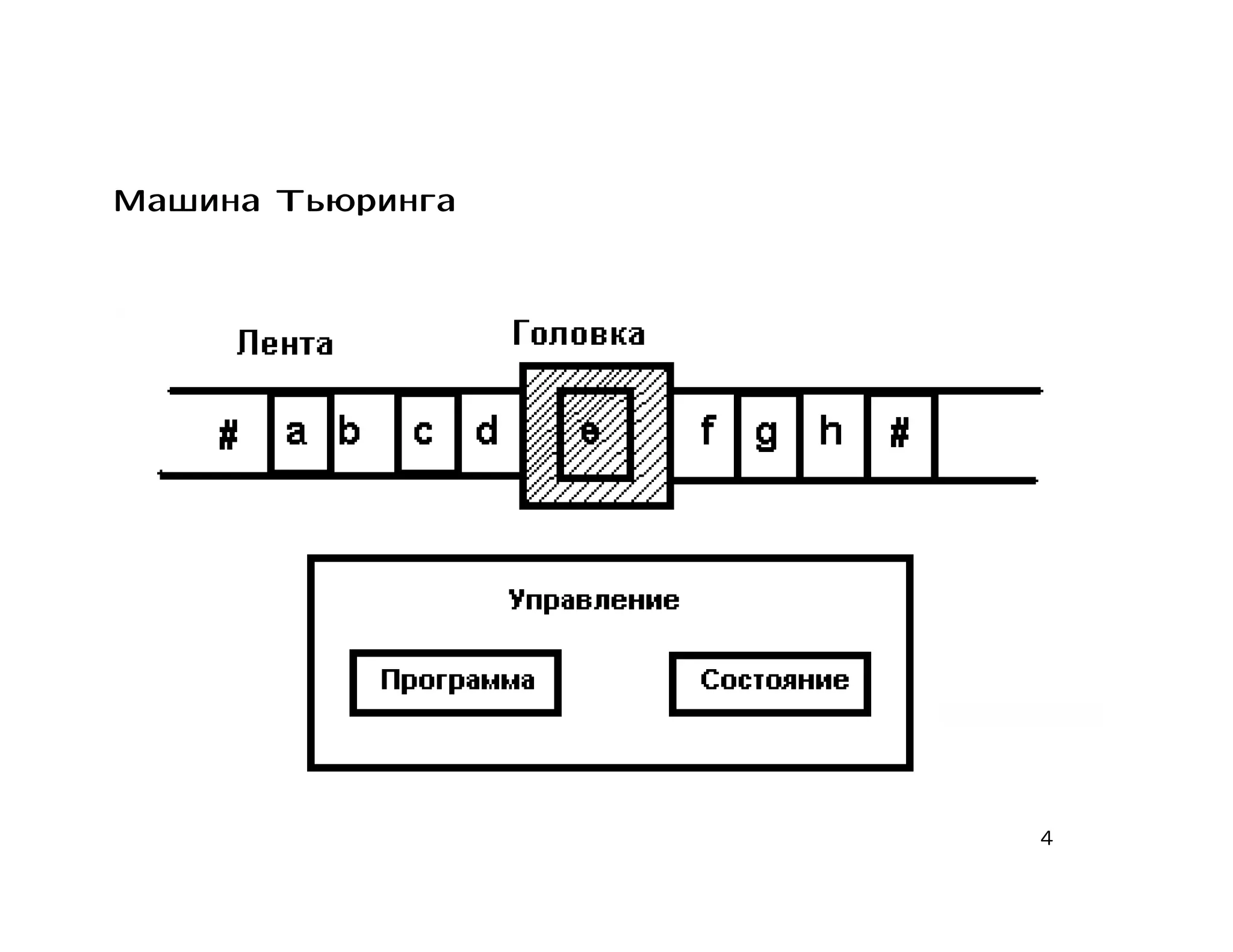
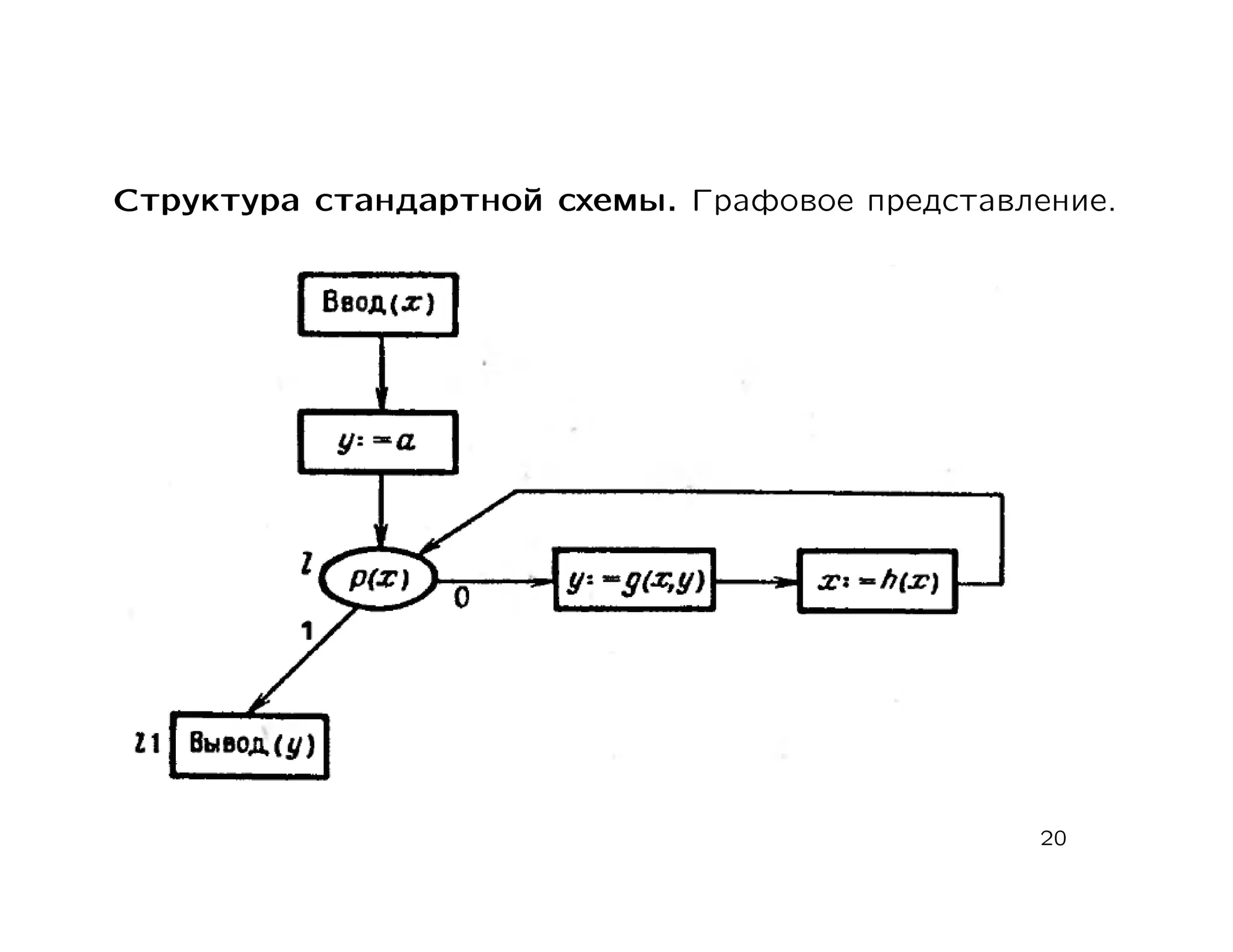
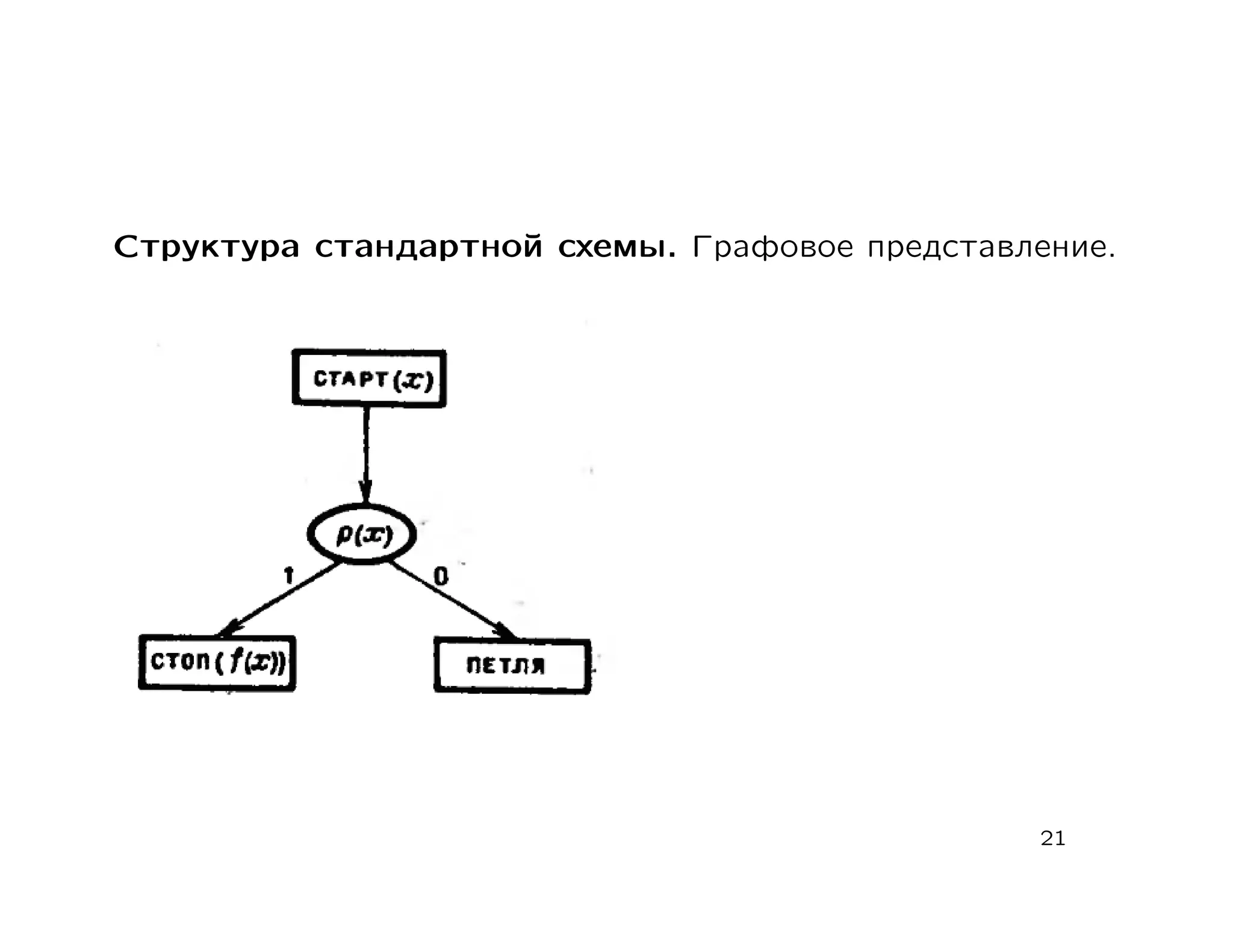
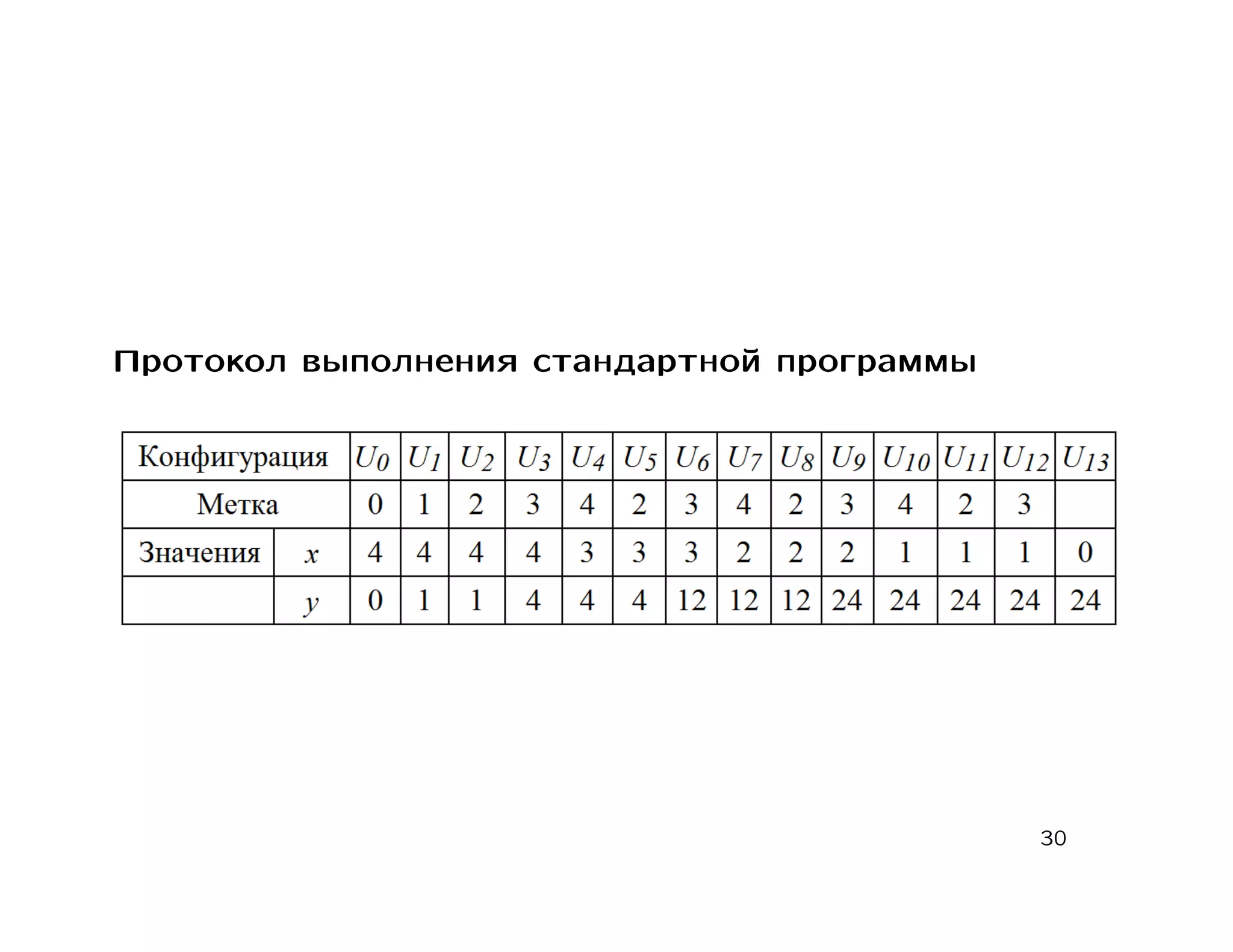
Документ представляет собой лекцию о теории вычислительных процессов, в которой обсуждаются машины Тьюринга, вычислимые функции и алгоритмические проблемы. Основное внимание уделяется конструктивным свойствам машин Тьюринга, алгоритмическим проблемам и различным типам схем программ. В конце представляется список литературы для дальнейшего изучения темы.

1. Хакасский государственный университет им. Н.Ф. Катанова
Теория вычислительных процессов
Лекция: Схемы программ:
алгоритмические проблемы, стандартные
схемы
Николай Гребенщиков, www.grebenshikov.ru

2. Вычислимость
Вычислимая функция - функция, которой можно задать
способ ее вычисления. (формула, алгоритм).
Машина Тьюринга - абстрактная математическая машина.
Тезис Тьюринга: для каждой функции, для которой суще-
ствует алгоритм нахождения ее значения, может быть по-
строена машина Тьюринга.
Эмпирический термин алгоритм ⇒ Тезиз не доказан!
Но опровергающие примеры также отсутствуют.
1

3. Машина Тьюринга - словарная функция:
• V - алфавит;
• Q конечное непустое множество символов, называемых
состояниями машины (Q V = );
• q0 выделенный элемент множества Q, называемый на-
чальным состоянием;
• # специальный пустой символ, не принадлежащий
ни V, ни Q;
• I программа машины.
2

4. Программа машины Тьюринга - конечное множество ко-
манд.
Команда: qa → q a d, где q, q ∈ Q, a, a ∈ V {#}; → вспо-
могательный символ-разделитель; d элемент множества
{l, r, }.
Никакие две команды не могут иметь одинаковую пару пер-
вых двух символов!
3

5. Машина Тьюринга
4

6. Работа машины Тьюринга
1. считывание символа, находящегося против головки;
2. поиск команды qa → q a d, в которой q текущее состо-
яние, считанный символ;
3. выполнение команды
Машина останавливается в том и только в том случае, если
на очередном шаге ни одна из команд не применима.
Результат работы заключительное слово на ленте оста-
новившейся машины.
5

7. Свойства машины Тьюринга
1. конструктивность МТ есть конечный объект, постро-
енный по определенным правилам из базовых объектов;
2. конечность нахождение значений для значений аргу-
ментов, для которых она определена, состоит из конеч-
ного числа шагов;
3. однозначность результат единственным образом опре-
деляется начальным словом;
4. массовость машина работает с любым начальным
словом, составленным из символов ее алфавита.
6

8. Автоматизация программирования - одна из целей изуче-
ния теоретического программирования.
Алгоритмические проблемы:
• узнать будет ли программа работать бесконечно;
• дают ли две программы одинаковый результат;
• является ли программа синтаксически правильной;
7

9. Алгоритмическая проблема, как проблема принадлеж-
ности множеству. Разрешимость. Перечислимость.
Пусть V – алфавит, M ⊆ V – множество слов в V .
Характеристическая функция множества M :
FM : V ∗ → {0, 1}, всюду определенный на V ∗ : FM (a) = 1, если
a ∈ M , и FM (a) = 0, если a ∈ M .
/
Частичная характеристическая функция множества M :
HM : V ∗ → {1}, определенная только для слов из M и имею-
щая вид HM (a) = 1 для всех a ∈ M .
8

10. Важные теоремы
1. Множество M ⊆ V ∗ разрешимо тогда и только тогда, ко-
гда M и его дополнение M = V ∗M перечислимы.
2. Проблема остановки машины Тьюринга неразрешима.
3. Проблема зацикливания машины Тьюринга не является
частично разрешимой.
9

11. Универсальная машина Тьюринга c 2003 Jin Wicked, USA.
10

12. Схема программы - математическая модель программы,
описывающая строение программы, или точнее строение мно-
жества программ, где конкретные операции и функции заме-
нены абстрактными функциональными и предикатными сим-
волами.
11

13. Классы схемы программ
• Стандартные
• Рекурсивные
• Обогащенные
• Структурированные
12

14. Стандартные схемы программ - характеризуются базисом
и структурой.
13

15. Базис стандартных схем
• Переменные - X = {x, x1, x2, . . . , y, y1, y2, . . . , z, z1, z2, . . .}
• Функциональные символы -
F = {f (0), f (1), f (2), . . . , g (0), g (1), g (2), . . . , f (0), h(1), h(2), . . .}.
f 0, g 0, h0, . . . - константы, и обозначаются a, b, c, . . .
• Предикатные символы - P = {p(0), p(1), p(2), . . . , q (0), q (1), q (2)}.
p0, q 0, . . . - логические константы.
• Специальные символы - {start, stop, . . .}
14

16. Базис стандартных схем. Термы.
Термы (функциональные выражения) - слова, построенные
из переменных, функциональных и специальных символов по
следующим правилам:
• односимвольные слова, состоящие из переменных или кон-
стант, являются термами;
• слово τ вида f (n)(τ1, τ2, . . . , τn), где τ1, τ2, . . . , τn - термы,
является термом;
• те и только те слова, о которых говорится в п.п. 1,2,
являются термами.
Примеры термов: , f : (0), , f (1)(), g (2)(x, h(2)(y, a)).
15

17. Базис стандартных схем. Тесты.
Тесты (логические выражения) логические константы и сло-
ва вида p(n)(τ1, τ2, . . . , τn).
Примеры: p(0), p(1)(x), q (3)(x, y, z), p(1)(f (2)(x, y)).
Допускается в функциональных и логических выражениях
опускать индексы местности, если это не приводит к дву-
смысленности или противоречию.
16

18. Базис стандартных схем. Операторы.
• начальный оператор - слово вида start(x1, x2, . . . , xk ), где
k ≥ 0, а x1, x2, . . . , xk - переменные, называемые результа-
том этого оператора;
• заключительный оператор - слово вида stop(τ1, τ2, . . . , τn),
где n ≥ 0, а τ1, τ2, . . . , τn - термы; вхождения переменных
в термы τ называются аргументами этого оператора;
• оператор присваивания - слово вида x := τ , где x – пе-
ременная (результат оператора), а τ - терм; вхождения
переменных в термы называются аргументами этого опе-
ратора;
17

19. • условный оператор (тест) - логическое выражение; вхож-
дения переменных в логическое выражение называются
аргументами этого оператора;
• оператор петли - односимвольное слово loop.

20. Пример базиса стандартных схем
Подкласс V 1
{x1, x2}, {a, f (1)}, {p(1)}, {start, stop, (, ), :=, , },
{start(x1, x2); x1 := f (x1), x2 := f (x2),
x1 := a, x2 := a, p(1), p(x2), stop(x1, x2)}
18

21. Структура стандартной схемы. Графовое представление.
Стандартной схемой в базисе В - конечный размеченный ори-
ентированный граф без свободных дуг и с вершинами сле-
дующих пяти видов:
1. Начальная вершина (ровно одна) помечена начальным
оператором. Из нее выходит ровно одна дуга. Нет дуг,
ведущих к начальной вершине.
2. Заключительная вершина (может быть несколько). По-
мечена заключительным оператором. Из нее не выходит
ни одной дуги.
19

22. 3. Вершина-преобразователь. Помечена оператором присва-
ивания. Из нее выходит ровно одна дуга.
4. Вершина-распознаватель. Помечена условным операто-
ром (называемым условием данной вершины). Из нее вы-
ходит ровно две дуги, помеченные 1 (левая) и 0 (правая).
5. Вершина-петля. Помечена оператором петли. Из нее не
выходит ни одной дуги.

23. Структура стандартной схемы. Графовое представление.
20

24. Структура стандартной схемы. Графовое представление.
21

25. Структура стандартной схемы. Линейная форма.
Множество операторов необходимо расширить {goto, if, then, else}
0: start(х) goto 1,
1: у:=а goto 2,
2: if р(х) then 5 else 3,
3: у:=g(x,y) goto 4,
4: х:=h(x) goto 2,
5: stop(у).
22

26. Структура стандартной схемы. Сокращенная линейная фор-
ма.
start(х),
у:=а,
2: if р(х) then 5 else 3,
3: у:=g(x,y),
х:=h(x) goto 2,
5: stop(у).
23

27. Интерпретация стандартной схемы c базисом B в области
интерпретации D называется функция I, которая сопостав-
ляет:
1. каждой переменной x из базиса B - некоторый элемент
d = I(x) из области интерпретации D;
2. каждой константе a из базиса B - некоторый элемент
d = I(a) из области интерпретации D;
3. каждому функциональному символу f (n) - всюду опреде-
ленную функцию F (n) = I(f (n));
24

28. 4. каждой логической константе p(0) - один символ множе-
ства {0, 1};
5. каждому предикатному символу p(n) - всюду определен-
ный предикат P (n) = I(p(n)).

29. Стандартная программа - пара (S, I), где S - стандартная
схема, а I ее интерпертация.
Память схемы XS конечное множество переменных схемы S.
Состоянием памяти программы (S, I) называют функцию W :
XS → D, которая каждой переменной x из памяти схемы S
сопоставляет элемент W (x) из области интерпретации D.
Значение терма τ при интерпретации I и состоянии памяти
W (обозначим τI (W )) определяется следующим образом:
• если τ = x, x – переменная, то τI (W ) = W (x);
25

30. • если τ = a, a – константа, то τI (W ) = I(a);
• если τ = f (n)(τ1, τ2, . . . , τn), то
τI (W ) = I(f (n))(τ1I (W ), τ2I (W ), . . . , τnI (W ));
• если p = (n)(τ1, τ2, . . . , τn), то
pI (W ) = I(p(n))(τ1I (W ), τ2I (W ), ...τnI (W )), n ≥ 0

31. Выполнение стандартной программы
Конфигурация программы - пара U = (L, W ), где L - метка
вершины схемы S, а W - состояние ее памяти.
протоколом выполнения программы (ПВП) - конечная или
бесконечная последовательность конфигураций
(U0, U1, . . . , Ui, Ui+1, . . .) выполнения программы (S, I)
U 0 = (0, W0), W0 – начальное состояние памяти схемы S при
интерпретации I.
26

32. Выполнение стандартной программы Пусть Ui = (ki, Wi)
- i-я конфигурация ПВП, а O - оператор схемы S в вершине
с меткой ki, тогда Ui+1 = (ki+1, Wi+1)
• O = start(τ1, . . . , τn) и следующая вершина с меткой L, то
ki+1 = L и Wi+1 = Wi;
• O = x := τ и следующая вершина с меткой L, то ki+1 =
L, Wi+1 = Wi, Wi+1(x) = τI (Wi);
• O - условный оператор p и pI (Wi) = ∆, где ∆ ∈ {0, 1}и
следующая вершина с меткой L, то ki+1 = L и Wi+1 = Wi;
27

33. • O - оператор петли, то ki+1 = ki и Wi+1 = Wi, так что
протокол бесконечен.

34. Результат выполнения стандартной программы val(S, I)
выполнения программы (S, I) - последовательность значений
τ1I (W ), τ2I (W ), . . . , τnI (W ) из последней конфигурации прото-
коле, где O = stop(τ1, τ2, . . . τm)
28

35. Пример интерпретации
I1(x) = 4; I1(y) = 0; I1(a) = 1;
I1(g) = G, где G - функция умножения чисел, т. е. G(d1, d2) =
d1 ∗ d2 ;
I1(h) = H, где H - функция вычитания единицы, т. е. H(d) =
d − 1;
I1(p) = P 1, где P1 - предикат равно 0 , т.е. P1(d) = 1, если
d = 0.
29

36. Протокол выполнения стандартной программы
30

37. Список литературы
• Рабинович Е.В. Теория вычислительных процессов. Раз-
дел “Стандартные схемы” .
• Котов В.Е., Сабельфельд В.К. Теория схем программ. -
М.: Наука, 1991. - 248 с. сс.1-91.
31