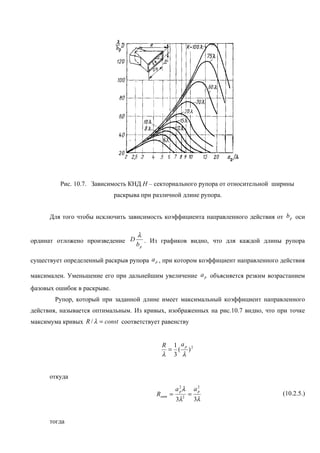
Документ обсуждает анализ работы секториального рупора в цилиндрической системе координат, включая формулы для описания компонентов поля и фазовых искажений. Приведены приближенные формулы для определения максимального фазового сдвига, а также зависимость коэффициента направленного действия от параметров рупора. Установлены оптимальные соотношения между длиной рупора и его раскрытием для достижения максимального коэффициента направленного действия.

1. 10.2.1. H – плоскостной секториальный рупор.
Для нахождения структуры поля в рупоре используем цилиндрическую систему координат
y, ρ , ϕ .
Волна H 10 будет иметь компоненты H ρ , H ϕ , и E y .
Рис. 10.5. Цилиндрическая система координат для анализа секториальных рупоров.
Решая систему уравнений Максвелла и используя асимптотические выражения функций
Ганкеля для больших значений аргумента kρ , получаем следующие значения для составляющих
поля
ρ0 π ϕ − j ( kρ −ψ
E y = E0 cos( )e 0 )
ρ 2 ϕ0
H ϕ = − E y / 120π (10.2.1.)
E0 ρ0 π ϕ − j ( kρ −ψ
Hρ = − j sin( )e 0 )
240ϕ 0 kρ ρ 2 ϕ0
H y = Eϕ = E ρ = 0 .
Здесь E 0 − напряженность электрического поля в точке рупора с координатами y = 0, ϕ = 0,
ρ = ρ 0 причем ρ 0 >> λ .
Формулы (10.2.1.) показывают, что при больших kρ составляющая H ρ → 0 и поле в
рупоре представляет собой поперечную электромагнитную цилиндрическую волну. Вследствие
того, что у большинства применяемых рупоров раскрыв плоский, а волна в рупоре
цилиндрическая, поле в раскрыве не будет синфазным.
Для определения фазовых искажений в раскрыве рассмотрим продольное сечение рупора.
Дуга окружности с центром в вершине рупора О проходит по фронту волны и, следовательно,
является линией равных фаз. В произвольной точке M ′ , имеющей координату x , фаза поля
отстает от фазы в середине раскрыва (в точке O ′ ) на угол

2. 2π 2π 2π x 2 x4
∆ϕ x = (OM ′ − R ) = ( R 2 + x 2 − R) = ( − 3 + )
λ λ λ 2R 8R
Рис. 10.6. К определению фазовых искажений в раскрыве рупора.
Так как обычно в рупорах x << R , то можно ограничиться первым членом разложения
πx 2
∆ϕ k = (10.2.2.)
λR
πa 2
p
∆ϕ max = (10.2.3.)
4λ R
Формула (10.2.2.) и (10.2.3.) является приближенными. Ими можно пользоваться, когда
R > a p / 2 или ϕ 0 < 45 0 . В применяемых рупорах эти условия обычно выполняются.
Иногда удобно максимальные фазовые ошибки в раскрыве рупора определять через его
длину и половину угла раскрыва ϕ 0 .
2πR (1 − cos ϕ 0 )
∆ϕ max =
cos ϕ 0
Формула верна при любых R и ϕ 0 .
Из формулы (10.2.3.) видно, что при заданной a p поле в раскрыве будет тем меньше
отличаться от синфазного, чем больше длина рупора R . Габаритные ограничения требуют
нахождения компромиссного решения, т.е. определения такой длины рупора, при которой
максимальный фазовый сдвиг в его раскрыве не будет превышать некоторой допустимой
величины. Эта величина обычно определяется наибольшим значением коэффициента
направленного действия, которое можно получить от рупора заданной длины. Для H −
3π
секториального рупора максимально допустимый фазовый сдвиг составляет ∆ϕ max = , что
4
соответствует следующему соотношению между оптимальной длиной рупора, размером раскрыва
a p и длиной волны λ :

3. a2
p
Rопт =
3λ
Для определения распределения амплитуд поля в раскрыве рупора примем
ϕ x′
ρ ≈ R, ≈ , Hϕ ≈ −H x
2ϕ 0 a p
Таким образом, поле в раскрыве H − секториального рупора окончательно представим
выражениями
 πx 2
πx ′ − j
 E y = E 0 cos( )e λ R
 ap
 H = − E / 120π
 x y
Диаграмма направленности в плоскости E
kb p
sin( sin θ )
1 + cosθ 2
FE (θ ) = (10.2.4.)
2 kb p
sin θ
2
Характерные зависимости коэффициента направленного действия от относительного
раскрыва рупора a p / λ для различных длин рупора приведены ниже.

4. Рис. 10.7. Зависимость КНД Н – секториального рупора от относительной ширины
раскрыва при различной длине рупора.
Для того чтобы исключить зависимость коэффициента направленного действия от b p оси
λ
ординат отложено произведение D . Из графиков видно, что для каждой длины рупора
bp
существует определенный раскрыв рупора a p , при котором коэффициент направленного действия
максимален. Уменьшение его при дальнейшим увеличение a p объясняется резким возрастанием
фазовых ошибок в раскрыве.
Рупор, который при заданной длине имеет максимальный коэффициент направленного
действия, называется оптимальным. Из кривых, изображенных на рис.10.7 видно, что при точке
максимума кривых R / λ = const соответствует равенству
R 1 ap 2
= ( )
λ 3 λ
откуда
a2λ
p a2
p
Rопт = = (10.2.5.)
3λ2 3λ
тогда

5. 3
∆ϕ max = π .
4
Если длину рупора взять больше Rопт , то при той же площади раскрыва коэффициента
направленного действия возрастает, но не очень сильно. Точкам максимума коэффициента
направленного действия соответствует коэффициент использования площади раскрыва ν = 0.64 .
Если длину рупора непрерывно увеличивать, то в пределе при R → ∞ мы получим
синфазное поле в раскрыве рупора. Коэффициент использования синфазной площадки с
косинусоидальным распределением амплитуды поля равен ν = 0.81 . Таким образом увеличение
длины рупора по сравнению с его оптимальной длиной не может повысить коэффициент
направленного действия более чем на 20%.
Коэффициент полезного действия рупорных антенн вследствие малых потерь практически
может быть принят за единицу.