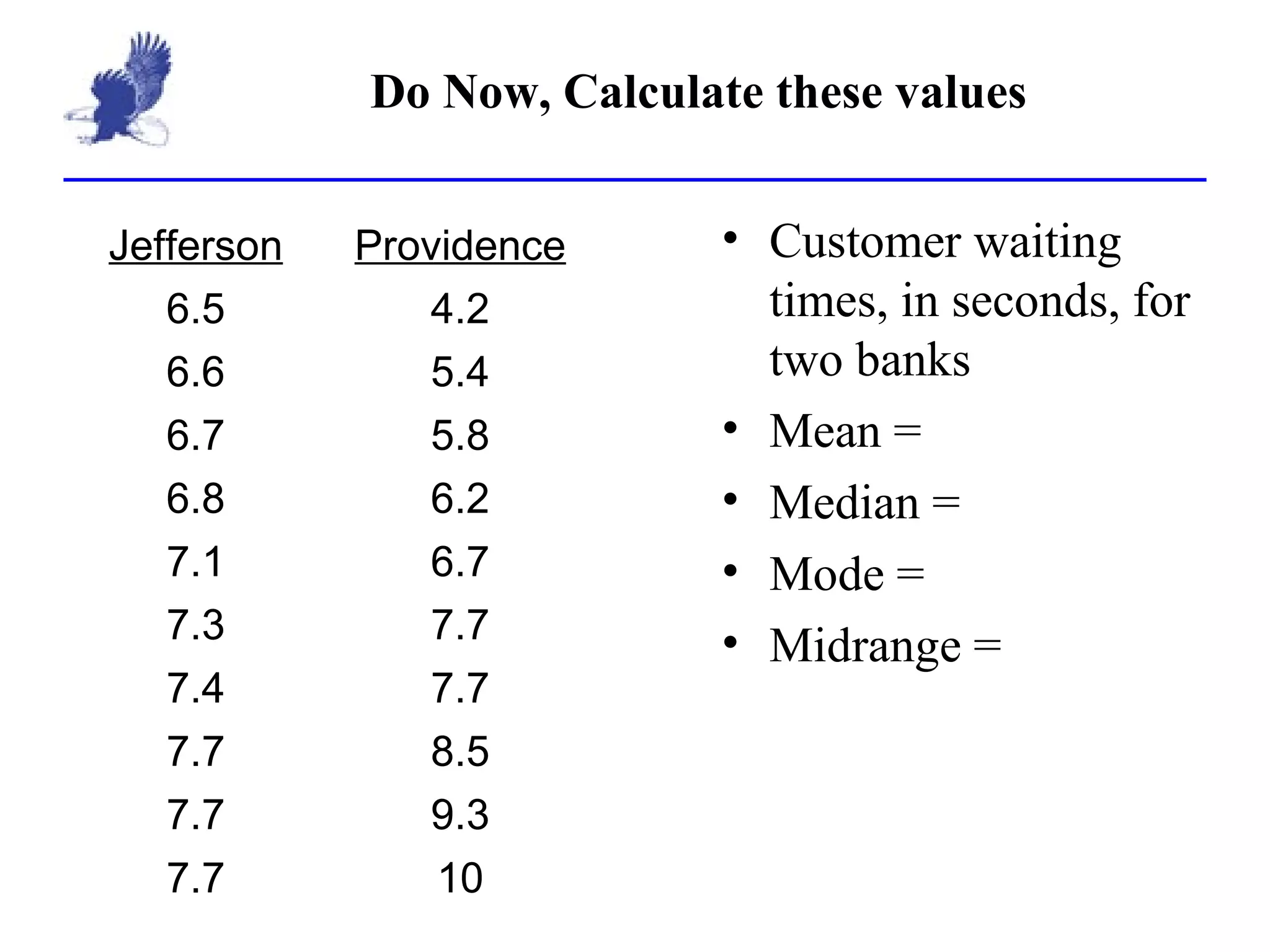
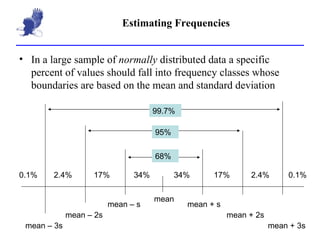
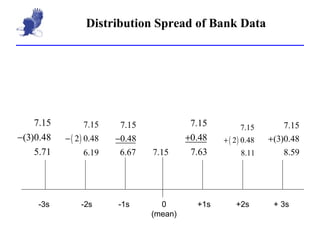
The document discusses measures of central tendency and variation such as mean, median, mode, range, standard deviation, and variance. It provides examples of calculating standard deviation and using the mean and standard deviation to build a normal distribution frequency table. Standard deviation measures how far values are from the mean, with about 2/3 of values within 1 standard deviation and 95% within 2 standard deviations of the mean. Outliers are values more than 2 standard deviations from the mean.

1. Do Now, Calculate these values Customer waiting times, in seconds, for two banks Mean = Median = Mode = Midrange = Providence Jefferson 10 7.7 9.3 7.7 8.5 7.7 7.7 7.4 7.7 7.3 6.7 7.1 6.2 6.8 5.8 6.7 5.4 6.6 4.2 6.5

2. Measures of Variation We need to measure the variation in such a way that Data in which values that are close together should have a small measurement Values that are spread apart should have a high measurement Range Standard deviation Variance

3. Range maximum - minimum Jefferson: Providence:

4. Standard Deviation “Measurement of variation of values about their mean” Standard deviation based on a sample : Abbreviated s Same units as the original values Sample variance = s 2

5. Population Standard Deviation Standard deviation of the entire population: Abbreviated σ (lower-case sigma) Same units as the original values Population variance = σ 2

6. Standard Deviation Interpretation “Average distance from the mean” About 2/3 of the values should fall within 1 standard deviation of the mean Can be estimated with the Range rule of thumb :

7. Calculating a Standard Deviation Find the mean For each value Subtract the mean from the value Square the difference Add the squares from step 2b. Divide that sum buy one less than number of samples Find the square root of the quotient

8. Live Example: Jefferson Valley 7.7 7.7 7.7 6.5 7.4 7.3 7.1 6.8 6.7 6.6

9. Your turn: Providence 6.2 5.8 5.4 4.2 6.7 7.7 10 9.3 8.5 7.7

10. Rounding Round to one more decimal place that the original data. E.g., the mean of 14 15 9 16 and 12 would be 13.2 E.g., the mean of 1.04, 2.17, and 3.79 would be 2.333 Except for ‘well-know’ decimals 0.25, 0.75, 0.5 Round the standard deviation to one more place that the mean

11. Homework Find the standard deviation of Super Bowl Points Use the range rule of thumb to estimate the standard deviation of motor vehicle deaths and Sunspot number

12. Uses Standard Deviation Interpretation “Average distance from the mean” About 2/3 of the values should fall within 1 standard deviation of the mean Uses Identify outliers and determining what is “unusual” Frequency Tables Curving

13. Estimating Frequencies In a large sample of normally distributed data a specific percent of values should fall into frequency classes whose boundaries are based on the mean and standard deviation mean mean + s mean + 2s mean + 3s mean – 3s mean – 2s mean – s 34% 34% 17% 17% 2.4% 2.4% 0.1% 0.1% 68% 95% 99.7%

14. Distribution Spread of Bank Data 0 (mean) +1s +2s + 3s -3s -2s -1s

15. Outliers and Unusual Values 5% is considered the boundary for being unusual Values are considered outliers or unusual if they are beyond 2 standard deviations from the mean. mean mean + 2s mean – 2s 2.5% 2.5% 95%

16. Outliers and Unusual Values Outliers and/or unusual values are usually investigated Different category Bad data “Bad day” Outliers and/or unusual values might be trimmed from the list

17. Frequency Table We can use the mean and standard deviation as the boundary of our frequency classes If the data is normally distributed 68% of our samples should be within one standard deviation of the mean 95% should be within two standard deviations 99.7 should be within three standard deviations

18. Building a Frequency Table Create a table of six classes Find the mean and standard deviation Use the mean as the lower class fourth class Add the standard deviation to the mean to get the LCL for the fifth classes, add it again for the LCL for the sixth the mean. Subtract the standard deviation from the mean to get the LCL for the third class, subtract it again to get the LCL for the second class. The first class has no LCL Fill in the UCLs; the sixth class has no UCL Fill in the frequencies

19. IQ Scores The mean and standard deviation for IQ scores is 100 and 15, respectively. Create a frequency table for the following IQ scores: 100 111 122 95 83 95 109 93 102 110 86 98 120 108 117 94 101 105 104 72

20. IQ Frequency Table Frequency UCB LCB

21. Using Mean and Std Dev to curve a tests 25 55 59 59 63 71 71 74 80 80 80 83 84 84 87 88 95 95 100 100 X-bar is 77, s is 18 Use s divided by 3 for grade boundaries C+ B B+ A F D D+ C A+

22. Your Turn Define distribution spread and a frequency table using the following values: 50 140 104 75 55 22 75 39 90 45 110 62 90 35 200 90 Are there any “unusual values? What is the “theoretical” percent of values that fall within 1 sigma? What is the actual percent of values that fall within 1 sigma?

23. IQ Frequency Table Frequency UCB LCB

24. Homework The mean adult male height is 69 inches; the standard deviation is 3.5 The mean adult female height is 64 inched; the standard deviation is 3 On the next slide use these values to create a frequency table of your opinion poll data. Identify outliers/unusual values

25. Frequency Table: Male Frequency UCB LCB

26. Frequency Table: Female Frequency UCB LCB