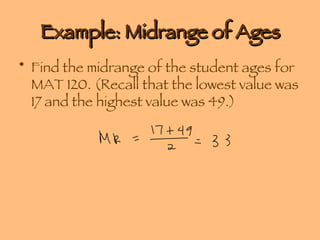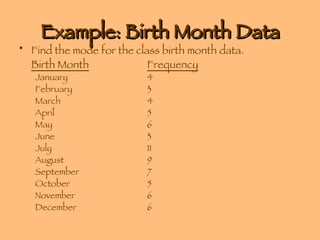
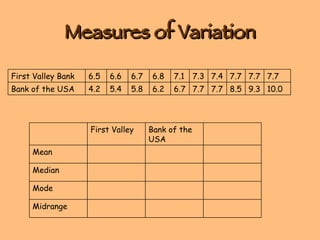
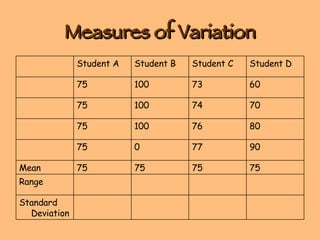
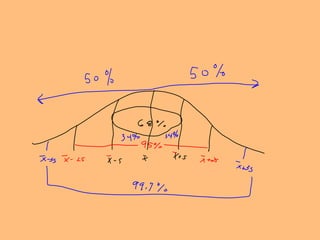
This document provides an overview of key concepts in descriptive statistics including: - Parameters describe populations while statistics describe samples - Measures of central tendency include the mean, median, and mode - Measures of variation/dispersion include range, variance, standard deviation, and coefficient of variation - The empirical rule describes how many data points fall within a certain number of standard deviations from the mean for a normal distribution

1. Chapter 3: Data Description

2. Parameter vs. Statistic A statistic is a characteristic or measure obtained by using the data values from a sample. A parameter is a characteristic or measure obtained by using all the data values for a specific population.

3. Parameter vs. Statistic In statistics Greek letters are used to denote parameters and Roman letters are used to denote statistics. Assume that the data are obtained from samples unless otherwise specified.

4. Measures of Central Tendency: Mean The mean is the sum of the values, divided by the total number of values. The symbol represents the sample mean where n represents the total number of values in the sample.

5. Measures of Central Tendency: Mean For a population the Greek letter  is used for the mean. _________________________________ where N represents the total number of values in the population.

6. Example: Chief Justices The lengths of service (in years) of eight of the Chief Justices of the Supreme Court are 7, 1, 5, 35, 28, 10, 15, 22. Find the mean.

7. What Makes the Mean a Center? 1 5 7 10 15 22 28 35

8. Measures of Central Tendency: Mean The mean should be rounded to one more decimal place that occurs in the raw data.

9. Measures of Central Tendency: Mean To estimate the mean from a frequency distribution, use the class midpoint to represent each class. ____________________________

10. Example: Mean Age of 120 Students Approximate the mean age for students in MAT 120. Class Frequency( ) Midpoint( ) ______ 15 – 19 16 20 – 24 34 25 – 29 12 30 – 34 5 35 – 39 1 40 – 44 0 45 – 49 1

11. Measures of Central Tendency: Median The median is the midpoint of the data array. To find the median, the data must be arranged in order.

12. Example: Supreme Court Justices Find the median value for the lengths of service for the sample of Supreme Court Justices 7, 1, 5, 35, 28, 10, 15, 22.

13. Example: Hospital System Example: The number of hospitals for the five largest hospital systems is shown here. Find the median. 340, 75, 123, 259, 151

14. Measures of Central Tendency: Mode The value that occurs most often in a set of data is called the mode . Find the mode for 5, 6, 2, 4, 2, 3, 6, 4, 1, 2 A set of data that has two modes is called bimodal. A data set may also have no mode.

15. Example: Birth Month Data Find the mode for the class birth month data. Birth Month Frequency January 4 February 3 March 4 April 5 May 6 June 3 July 11 August 9 September 7 October 5 November 6 December 6

16. Measures of Central Tendency: Mode The mode for grouped data is the modal class . The modal class is the class with the largest frequency. Age Distribution of MAT 120 Students Classes Frequencies 15 –19 16 20 –24 34 25 –29 12 30 –34 5 35 –39 1 40 –44 0 45 –49 1

17. Measures of Central Tendency: Midrange The midrange is defined as the sum of the lowest and highest values in the data set, divided by 2. The symbol MR is used for the midrange. _____ = _________________

18. Example: Midrange of Ages Find the midrange of the student ages for MAT 120. (Recall that the lowest value was 17 and the highest value was 49.)

19. Measures of Central Tendency: Weighted Mean Find the weighted mean of a variable X by multiplying each value by its corresponding weight and dividing the sum of the products by the sum of the weights __________________________________

20. Example: Weighted Mean Example: An instructor grades exams 20%; term paper, 30%; final exam, 50%. A student had grades of 83, 72, and 90, respectively, for exams, term paper, and final exam. Find the student’s final average.

21. Example: Weighted Mean Example: A student has the following grades for the Fall term: MAT 120 (3 hrs), A; BIO 210 (4 hrs), B; HIS 201, 3 (hrs) C; SOC 101 (3 hrs), A; CPT 170 (3 hrs), A. Calculate the student’s GPA for the fall term.

22. Example: Weighted Mean Example: In a dental survey of third grade students, this distribution was obtained for the number of cavities found. Find the average number of cavities. Number of Students Number of Cavities 12 0 8 1 5 2 5 3

24. Measures of Variation 10.0 9.3 8.5 7.7 7.7 6.7 6.2 5.8 5.4 4.2 Bank of the USA 7.7 7.7 7.7 7.4 7.3 7.1 6.8 6.7 6.6 6.5 First Valley Bank Midrange Mode Median Mean Bank of the USA First Valley

25. Back-to-Back Stem & Leaf Plot First Valley Bank Bank of the USA 10.0 9.3 8.5 7.7 7.7 6.7 6.2 5.8 5.4 4.2 Bank of the USA 7.7 7.7 7.7 7.4 7.3 7.1 6.8 6.7 6.6 6.5 First Valley Bank

26. Range The range is the highest value minus the lowest value. The symbol R is used for the range. ____________________ The range is affected by extremely high or low values. The range is easy to compute. Example: Determine the range for the First Valley Bank and the Bank of USA. Range First Valley _______ Bank of USA _______

27. Measures of Variation Standard Deviation Range 75 75 75 75 Mean 90 77 0 75 80 76 100 75 70 74 100 75 60 73 100 75 Student D Student C Student B Student A

28. Deriving the Variation and Standard Deviation Formulas

29. Population Variance & Standard Deviation The variance is the average of the squares of the distance each value is from the mean. The symbol for the population variance is  2 . The formula for the population variance is ______________________________ The standard deviation is the square root of the variance. The symbol for the population standard deviation is  . The formula for the population standard deviation is ____________________.

30. Sample Variance & Standard Deviation The formula for the sample variance, denoted by s 2 is _____________ The standard deviation for a sample is ____=______ =____________

31. Example: Use your calculator to determine the standard deviation and variance for the First Valley Bank and the Bank of USA. Variance Standard Deviation First Valley _______ _________ Bank of USA_______ _________

32. Finding the Standard Deviation From a Frequency Distribution Example: Use your calculator to approximate the variance and standard deviation for the age for students in MAT 120. Class Frequency (___) Midpoint (____) _______ 15 – 19 16 20 – 24 34 25 – 29 12 30 – 34 5 35 – 39 1 40 – 44 0 45 – 49 1

33. Coefficient of Variation The coefficient of variation is the standard deviation divided by the mean. It allows one to compare standard deviations when the units are different. _________________________

34. Example The average score on an English final exam was 85, with a standard deviation of 5. The average score on a history final exam was 110 with a standard deviation of 8. Which class was more variable?

35. Chebyshev’s Theorem The proportion of values from a data set that will fall within k standard deviations of the mean will be at least __________, where k is a number greater than 1.

36. Empirical Rule – For data that is bell-shaped, the following statements make up the Empirical Rule. Approximately 68% of the data values will fall within 1 standard deviation of the mean. Approximately 95% of the data values will fall within 2 standard deviations of the mean Approximately 99.7% of the data values will fall within 3 standard deviations of the mean

38. Empirical Rule Example A study of the number of paid sick days taken per year by employees results in a mound-shaped distribution with a mean of 8.7 and a standard deviation or 3. According to the empirical rule, what percentage of employees were taking between 2.7 and 14.7 paid sick days per year?

39. Example A bakery makes loaves of rye bread that have an average weight of 28 ounces and a standard deviation of 0.8 ounce. The distribution of weights is mound shaped. About 95% of the loaves will have weights that lie within what interval?

40. Example A bakery makes loaves of rye bread that have an average weight of 28 ounces and a standard deviation of 0.8 ounce. The distribution of weights is mound shaped. Nearly all the loaves will have weights that lie within what interval?

41. Example A bakery makes loaves of rye bread that have an average weight of 28 ounces and a standard deviation of 0.8 ounce. The distribution of weights is mound shaped. Approximately what percentage of loaves will weigh more than 28.8 ounces?

42. Example A taxi company has found that its fares average $7.80 with a standard deviation of $1.40. What can we say about the percentage of fares that are between $5.00 and $10.60 if A. The distribution of fares is mound shaped?

43. A taxi company has found that its fares average $7.80 with a standard deviation of $1.40. What can we say about the percentage of fares that are between $5.00 and $10.60 if B. The distribution of fares in not mound shaped?

44. Example: A pharmaceutical company manufactures capsules that contain an average of 507 grams of vitamin C. The standard deviation is 3 grams. At least 96 percent of the capsules will contain what amount of vitamin C?

45. Measures of Position A z-score or standard score for a value is obtained by subtracting the mean from the value and dividing the result by the standard deviation. The formula is _________________________ ____________ ____________

46. The z-score represents the number of standard deviations that a data value falls above or below the mean.

47. Example A student scores 60 on a mathematics test that has a mean of 54 and a standard deviation of 3, and she scores 80 on a history test with a mean of 75 and a standard deviation of 2. On which test did she perform better?

48. Percentiles Percentiles divide the data set into 100 equal groups. The percentile corresponding to a given value X is computed using the following formula ______________________

49. Find a Data Value Corresponding to a Given Percentile Arrange the data in order from highest to lowest Substitute into the formula __________ where __________ and ____________ If c is not a whole number, round up to the next whole number. Starting at the lowest value, count over to the number that corresponds to the rounded-up value. If c is a whole number, use the value halfway between the c th and (c + 1) th values when counting up from the lowest value.

50. Example The data given are weights are in pounds. 78, 82, 86, 88, 92, 97 Find the percentile rank of each weight in the data set. What value corresponds to the 30th percentile?

51. Example a. Find the percentile rank for each test score in the data set. 12, 28, 35, 42, 47, 49, 50 What value corresponds to the 60th percentile?