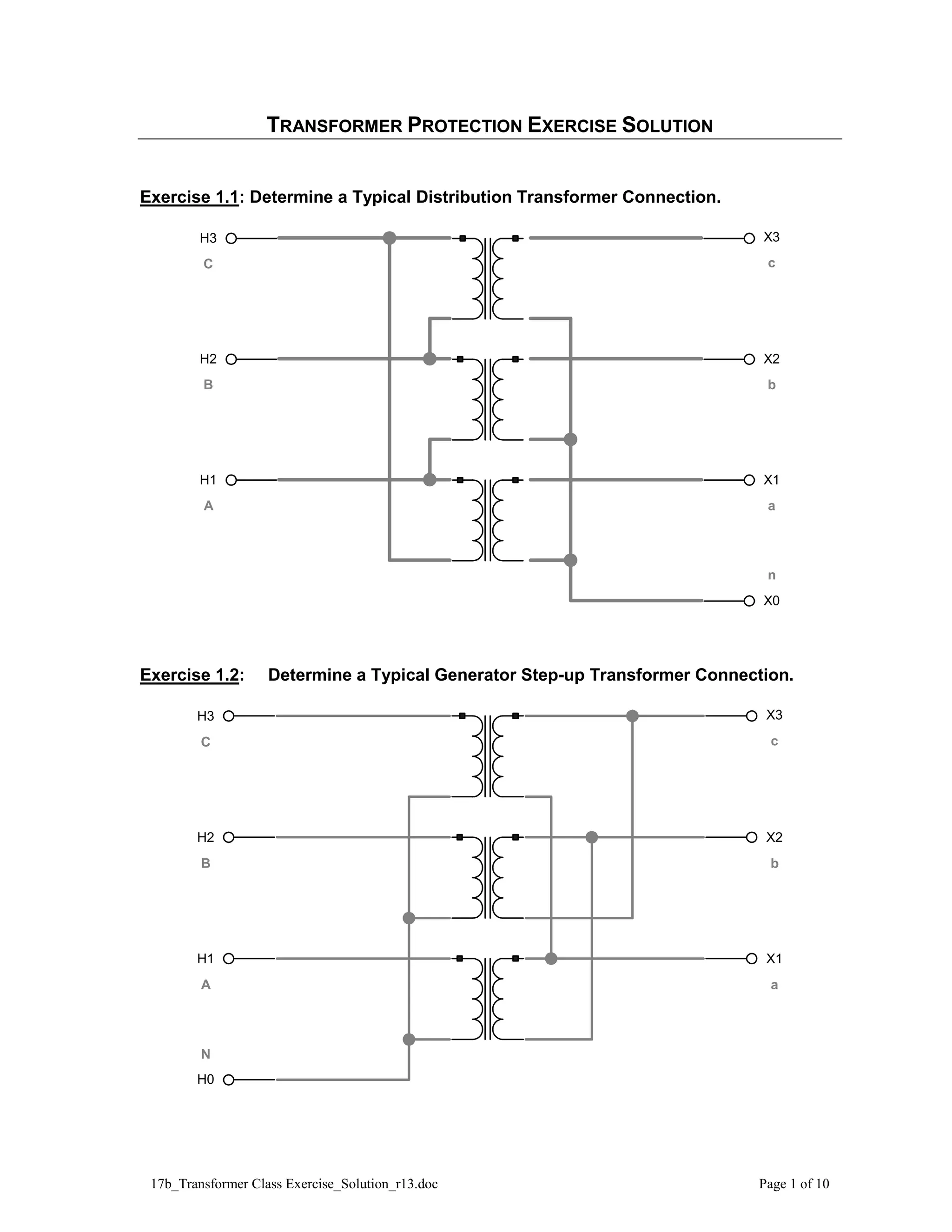
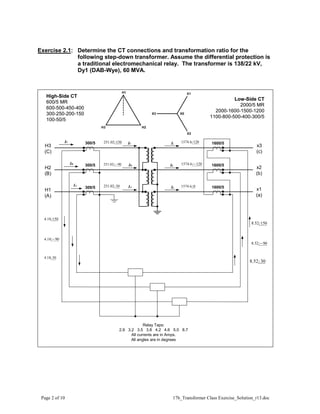
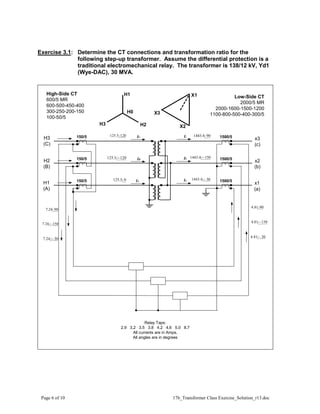
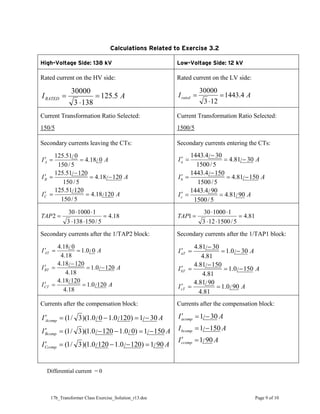
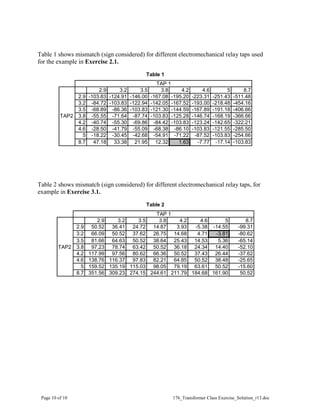
This document provides solutions to exercises related to transformer protection. Exercise 1 asks students to determine typical distribution and generator step-up transformer connections. Exercise 2 involves calculating currents and selecting CT ratios and relay taps for a 138/22 kV transformer. Exercise 3 repeats these calculations for a 138/12 kV transformer. The exercises help students learn to analyze transformer connections and settings for differential relay protection.

1. 17b_Transformer Class Exercise_Solution_r13.doc Page 1 of 10
TRANSFORMER PROTECTION EXERCISE SOLUTION
Exercise 1.1: Determine a Typical Distribution Transformer Connection.
H3
H2
H1
X3
X2
X1
X0
C
B
A
c
b
a
n
Exercise 1.2: Determine a Typical Generator Step-up Transformer Connection.
H3
H2
H1
X3
X2
X1
H0
C
B
A
c
b
a
N

2. Page 2 of 10 17b_Transformer Class Exercise_Solution_r13.doc
Exercise 2.1: Determine the CT connections and transformation ratio for the
following step-down transformer. Assume the differential protection is
a traditional electromechanical relay. The transformer is 138/22 kV,
Dy1 (DAB-Wye), 60 MVA.
H1
(A)
H2
(B)
H3
(C)
x1
(a)
x2
(b)
x3
(c)
H1
H2
H3
X2
X3
X1
X0
Ib
Ia
Ic
IC
IB
IA
Relay Taps:
2.9 3.2 3.5 3.8 4.2 4.6 5.0 8.7
All currents are in Amps.
All angles are in degrees
300/5
300/5
300/5
1600/5
1600/5
1600/5
150
/
02
.
251
90
/
02
.
251 −
30
/
02
.
251
150
/
18
.
4
90
/
18
.
4 −
30
/
18
.
4
150
/
52
.
8
90
/
52
.
8 −
30
/
52
.
8
120
/
6
.
1574
120
/
6
.
1574 −
0
/
6
.
1574
High-Side CT
600/5 MR
600-500-450-400
300-250-200-150
100-50/5
Low-Side CT
2000/5 MR
2000-1600-1500-1200
1100-800-500-400-300/5
High-Side CT
600/5 MR
600-500-450-400
300-250-200-150
100-50/5
Low-Side CT
2000/5 MR
2000-1600-1500-1200
1100-800-500-400-300/5
IC
IB
IA

3. 17b_Transformer Class Exercise_Solution_r13.doc Page 3 of 10
Calculations for Exercise 2.1
High-Voltage Side: 138 kV Low-Voltage Side: 22 kV
Current transformers must be connected in:
Y . Draw the connection diagram on the
figure.
Current transformers must be connected in:
DELTA. Draw the connection diagram on
the figure.
Rated current on the HV side:
A
IRATED 02
.
251
138
3
60000
=
⋅
=
Rated current on the LV side:
A
Irated 6
.
1574
22
3
60000
=
⋅
=
Current Transformation Ratio Selected:
300/5
Current Transformation Ratio Selected:
1600/5
Secondary currents entering the relays:
A
I
A
I
A
I
C
B
A
150
/
18
.
4
5
/
300
150
/
02
.
251
90
/
18
.
4
5
/
300
90
/
02
.
251
30
/
18
.
4
5
/
300
30
/
02
.
251
=
=
′
−
=
−
=
′
=
=
′
Secondary currents leaving the relays:
A
I
A
I
A
I
c
b
a
150
/
52
.
8
5
/
1600
150
/
6
.
1574
3
90
/
52
.
8
5
/
1600
90
/
6
.
1574
3
30
/
52
.
8
5
/
1600
30
/
6
.
1574
3
=
⋅
=
′
−
=
−
⋅
=
′
=
⋅
=
′
Differential current before balancing with the relay’s TAP compensation = |8.52-4.18| = 4.34 A
TAP Selection: 4.2 TAP Selection: 8.7
Mismatch: %
63
.
1
100
2
.
4
7
.
8
2
.
4
7
.
8
18
.
4
52
.
8
M =
⋅
−
= (See Table I at the end of this section).

4. Page 4 of 10 17b_Transformer Class Exercise_Solution_r13.doc
Exercise 2.2: Determine the TAP value and the compensation matrix for each side of
the differential protection shown in the figure. Determine the value of
current for each branch of the circuit. Fill in all the blanks. The
transformer is 138/22 kV, Dy1 (DAB-Wye), 60 MVA.
H1
(A)
H2
(B)
H3
(C)
x1
(a)
x2
(b)
x3
(c)
1/TAP1
COMPENSATION
MATRIX
COMPENSATION
MATRIX
DIFF.
TAP1= TAP2=
4.18 4.92
1 0 0
0 1 0
1
0
0
1 -1 0
0 1 -1
1
0
-1
All currents are in Amps.
All angles are in degrees
300/5
300/5
300/5
1600/5
1600/5
1600/5
1/TAP2
150
/
02
.
251
90
/
02
.
251 −
30
/
02
.
251
150
/
18
.
4
90
/
18
.
4 −
30
/
18
.
4
150
/
0
.
1
90
/
0
.
1 −
30
/
0
.
1
120
/
0
.
1
120
/
0
.
1 −
0
/
0
.
1
150
/
0
.
1
90
/
0
.
1 −
30
/
0
.
1
150
/
0
.
1
90
/
0
.
1 −
30
/
0
.
1
120
/
92
.
4
120
/
92
.
4 −
0
/
92
.
4
120
/
6
.
1574
120
/
6
.
1574 −
0
/
6
.
1574
⋅
3
1
⋅
1

5. 17b_Transformer Class Exercise_Solution_r13.doc Page 5 of 10
Calculations Related to Exercise 2.2
High-Voltage Side: 138 kV Low-Voltage Side: 22 kV
Rated current on the HV side:
A
IRATED 02
.
251
138
3
60000
=
⋅
=
Rated current on the LV side:
A
Irated 6
.
1574
22
3
60000
=
⋅
=
Current Transformation Ratio Selected:
300/5
Current Transformation Ratio Selected:
1600/5
Secondary currents leaving the CT’s:
A
I
A
I
A
I
C
B
A
150
/
18
.
4
5
/
300
150
/
02
.
251
90
/
18
.
4
5
/
300
90
/
02
.
251
30
/
18
.
4
5
/
300
30
/
02
.
251
=
=
′
−
=
−
=
′
=
=
′
Secondary currents entering the CT’s:
A
I
A
I
A
I
c
b
a
120
/
92
.
4
5
/
1600
120
/
6
.
1574
120
/
92
.
4
5
/
1600
120
/
6
.
1574
0
/
92
.
4
5
/
1600
0
/
6
.
1574
=
=
′
−
=
−
=
′
=
=
′
18
.
4
5
/
300
138
3
1
1000
60
1 =
⋅
⋅
⋅
⋅
=
TAP 92
.
4
5
/
300
22
3
1
1000
60
2 =
⋅
⋅
⋅
⋅
=
TAP
Secondary currents after the 1/TAP1 block:
A
I
A
I
A
I
CT
BT
AT
150
/
0
.
1
18
.
4
150
/
18
.
4
90
/
0
.
1
18
.
4
90
/
18
.
4
30
/
0
.
1
18
.
4
30
/
18
.
4
=
=
′
−
=
−
=
′
=
=
′
Secondary currents after the 1/TAP2 block:
A
I
A
I
A
I
cT
bT
aT
120
/
0
.
1
92
.
4
120
/
92
.
4
120
/
0
.
1
92
.
4
120
/
92
.
4
0
/
0
.
1
92
.
4
0
/
92
.
4
=
=
′
−
=
−
=
′
=
=
′
Currents after the compensation block:
A
I
A
I
A
I
Ccomp
Bcomp
Acomp
150
/
1
90
/
1
30
/
1
=
′
−
=
′
=
′
Currents after the compensation block:
A
I
A
I
A
I
ccomp
bcomp
acomp
150
/
1
)
0
/
0
.
1
120
/
0
.
1
)(
3
/
1
(
90
/
1
)
120
/
0
.
1
120
/
0
.
1
)(
3
/
1
(
30
/
1
)
120
/
0
.
1
0
/
0
.
1
)(
3
/
1
(
=
−
=
′
−
=
−
−
=
′
=
−
−
=
′
Differential Current = 0

6. Page 6 of 10 17b_Transformer Class Exercise_Solution_r13.doc
Exercise 3.1: Determine the CT connections and transformation ratio for the
following step-up transformer. Assume the differential protection is a
traditional electromechanical relay. The transformer is 138/12 kV, Yd1
(Wye-DAC), 30 MVA.
H1
H2 X2
X3
X1
H0
x3
(c)
x2
(b)
x1
(a)
H3
(C)
H2
(B)
H1
(A)
IB
IC
IA Ia
Ib
Ic 1500/5
1500/5
1500/5
90
/
4
.
1443
150
/
4
.
1443 −
30
/
4
.
1443 −
90
/
81
.
4
150
/
81
.
4 −
30
/
81
.
4 −
90
/
24
.
7
150
/
24
.
7 −
30
/
24
.
7 −
0
/
5
.
125
120
/
5
.
125 −
120
/
5
.
125
H3
150/5
150/5
150/5
Relay Taps:
2.9 3.2 3.5 3.8 4.2 4.6 5.0 8.7
All currents are in Amps.
All angles are in degrees
High-Side CT
600/5 MR
600-500-450-400
300-250-200-150
100-50/5
Low-Side CT
2000/5 MR
2000-1600-1500-1200
1100-800-500-400-300/5

7. 17b_Transformer Class Exercise_Solution_r13.doc Page 7 of 10
Calculations for Exercise 3.1
High-Voltage Side: 138 kV Low-Voltage Side: 12 kV
Current transformers must be connected in:
DELTA. Draw the connection diagram on
the figure.
Current transformers must be connected in:
Y . Draw the connection diagram on the
figure.
Rated current on the HV side:
A
IRATED 5
.
125
138
3
30000
=
⋅
=
Rated current on the LV side:
A
Irated 4
.
1443
12
3
30000
=
⋅
=
Current Transformation Ratio Selected:
150/5
Current Transformation Ratio Selected:
1500/5
Secondary currents entering the relays:
A
I
A
I
A
I
C
B
A
90
/
24
.
7
5
/
150
90
/
5
.
125
3
150
/
24
.
7
5
/
150
150
/
5
.
125
3
30
/
24
.
7
5
/
150
30
/
5
.
125
3
=
⋅
=
′
−
=
−
⋅
=
′
−
=
−
⋅
=
′
Secondary currents leaving the relays:
A
I
A
I
A
I
c
b
a
90
/
81
.
4
5
/
1500
90
/
4
.
1443
150
/
81
.
4
5
/
1500
150
/
4
.
1443
30
/
81
.
4
5
/
1500
30
/
4
.
1443
=
=
′
−
=
−
=
′
−
=
−
=
′
Differential current before balancing with the relays’ TAP compensation = |7.24-4.81|=2.43 A
TAP Selection: 5.0 TAP Selection: 3.2
Mismatch: %
.
.
.
.
.
.
.
M 8
3
100
0
5
24
7
2
3
81
4
0
5
24
7
=
⋅
−
= (See Table II at the end of this section)

8. Page 8 of 10 17b_Transformer Class Exercise_Solution_r13.doc
Exercise 3.2: Determine the TAP value and the compensation matrix for each side of
the differential protection shown in the figure. Determine the value of
current for each branch of the circuit. Fill in all the blanks. The
transformer is 138/12 kV, Yd1 (Wye-DAC), 30 MVA.
x1
(a)
x2
(b)
x3
(c)
H1
(A)
H2
(B)
H3
(C)
COMPENSATION
MATRIX
COMPENSATION
MATRIX
DIFF.
TAP1=
TAP2=
4.81
4.18
All currents are in Amps.
All angles are in degrees
1500/5
1500/5
1500/5
150/5
150/5
150/5
1/TAP2
90
/
4
.
1443
150
/
4
.
1443 −
30
/
4
.
1443 −
90
/
81
.
4
150
/
81
.
4 −
30
/
81
.
4 −
90
/
0
.
1
150
/
0
.
1 −
30
/
0
.
1 −
120
/
0
.
1
120
/
0
.
1 −
0
/
0
.
1
120
/
18
.
4
120
/
18
.
4 −
0
/
18
.
4
120
/
5
.
125
120
/
5
.
125 −
0
/
5
.
125
1/TAP1
1 0 0
0 1 0
1
0
0
⋅
1
1 0 -1
-1 1 0
1
-1
0
⋅
3
1
30
/
0
.
1 −
150
/
0
.
1 −
90
/
0
.
1
30
/
0
.
1 −
150
/
0
.
1 −
90
/
0
.
1

9. 17b_Transformer Class Exercise_Solution_r13.doc Page 9 of 10
Calculations Related to Exercise 3.2
High-Voltage Side: 138 kV Low-Voltage Side: 12 kV
Rated current on the HV side:
A
IRATED 5
.
125
138
3
30000
=
⋅
=
Rated current on the LV side:
A
Irated 4
.
1443
12
3
30000
=
⋅
=
Current Transformation Ratio Selected:
150/5
Current Transformation Ratio Selected:
1500/5
Secondary currents leaving the CTs:
A
I
A
I
A
I
C
B
A
120
/
18
.
4
5
/
150
120
/
51
.
125
120
/
18
.
4
5
/
150
120
/
51
.
125
0
/
18
.
4
5
/
150
0
/
51
.
125
=
=
′
−
=
−
=
′
=
=
′
Secondary currents entering the CTs:
A
I
A
I
A
I
c
b
a
90
/
81
.
4
5
/
1500
90
/
4
.
1443
150
/
81
.
4
5
/
1500
150
/
4
.
1443
30
/
81
.
4
5
/
1500
30
/
4
.
1443
=
=
′
−
=
−
=
′
−
=
−
=
′
18
.
4
5
/
150
138
3
1
1000
30
2 =
⋅
⋅
⋅
⋅
=
TAP 81
.
4
5
/
1500
12
3
1
1000
30
1 =
⋅
⋅
⋅
⋅
=
TAP
Secondary currents after the 1/TAP2 block:
A
I
A
I
A
I
CT
BT
AT
120
/
0
.
1
18
.
4
120
/
18
.
4
120
/
0
.
1
18
.
4
120
/
18
.
4
0
/
0
.
1
18
.
4
0
/
18
.
4
=
=
′
−
=
−
=
′
=
=
′
Secondary currents after the 1/TAP1 block:
A
I
A
I
A
I
cT
bT
aT
90
/
0
.
1
81
.
4
90
/
81
.
4
150
/
0
.
1
81
.
4
150
/
81
.
4
30
/
0
.
1
81
.
4
30
/
81
.
4
=
=
′
−
=
−
=
′
−
=
−
=
′
Currents after the compensation block:
A
I
A
I
A
I
Ccomp
Bcomp
Acomp
90
/
1
)
120
/
0
.
1
120
/
0
.
1
)(
3
/
1
(
150
/
1
)
0
/
0
.
1
120
/
0
.
1
)(
3
/
1
(
30
/
1
)
120
/
0
.
1
0
/
0
.
1
)(
3
/
1
(
=
−
−
=
′
−
=
−
−
=
′
−
=
−
=
′
Currents after the compensation block:
A
I
A
I
A
I
ccomp
bcomp
acomp
90
/
1
150
/
1
30
/
1
=
′
−
=
−
=
′
Differential current = 0

10. Page 10 of 10 17b_Transformer Class Exercise_Solution_r13.doc
Table 1 shows mismatch (sign considered) for different electromechanical relay taps used
for the example in Exercise 2.1.
Table 1
Table 2 shows mismatch (sign considered) for different electromechanical relay taps, for
example in Exercise 3.1.
Table 2
2.9 3.2 3.5 3.8 4.2 4.6 5 8.7
2.9 -103.83 -124.91 -146.00 -167.08 -195.20 -223.31 -251.43 -511.48
3.2 -84.72 -103.83 -122.94 -142.05 -167.52 -193.00 -218.48 -454.16
3.5 -68.89 -86.36 -103.83 -121.30 -144.59 -167.89 -191.18 -406.66
TAP2 3.8 -55.55 -71.64 -87.74 -103.83 -125.28 -146.74 -168.19 -366.66
4.2 -40.74 -55.30 -69.86 -84.42 -103.83 -123.24 -142.65 -322.21
4.6 -28.50 -41.79 -55.09 -68.38 -86.10 -103.83 -121.55 -285.50
5 -18.22 -30.45 -42.68 -54.91 -71.22 -87.52 -103.83 -254.66
8.7 47.18 33.38 21.95 12.32 1.63 -7.77 -17.14 -103.83
TAP 1
2.9 3.2 3.5 3.8 4.2 4.6 5 8.7
2.9 50.52 36.41 24.72 14.87 3.93 -5.38 -14.55 -99.31
3.2 66.09 50.52 37.62 26.75 14.68 4.71 -3.81 -80.62
3.5 81.66 64.63 50.52 38.64 25.43 14.53 5.36 -65.14
TAP2 3.8 97.23 78.74 63.42 50.52 36.18 24.34 14.40 -52.10
4.2 117.99 97.56 80.62 66.36 50.52 37.43 26.44 -37.62
4.6 138.76 116.37 97.83 82.21 64.85 50.52 38.48 -25.65
5 159.52 135.19 115.03 98.05 79.19 63.61 50.52 -15.60
8.7 351.56 309.23 274.15 244.61 211.79 184.68 161.90 50.52
TAP 1