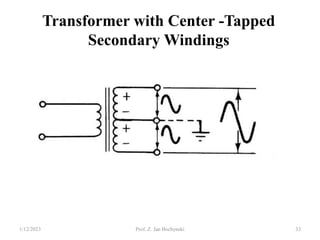
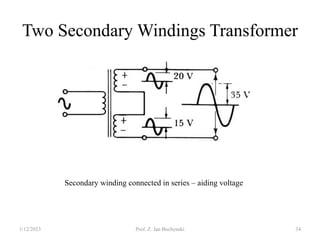
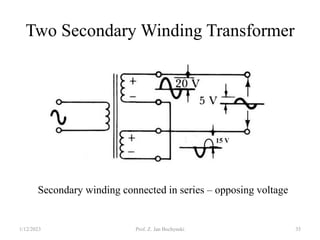
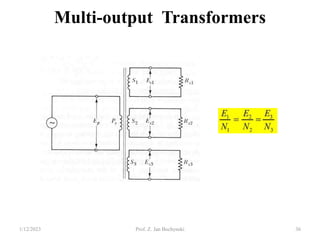
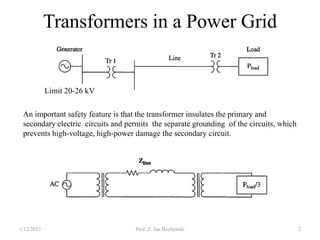
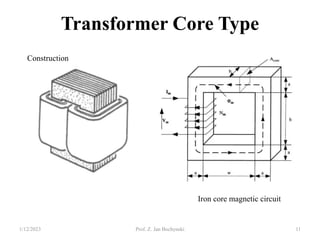
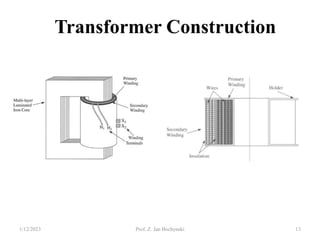
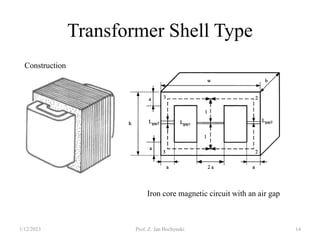
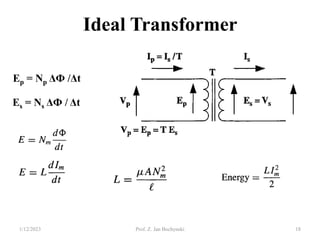
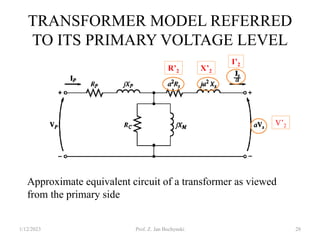
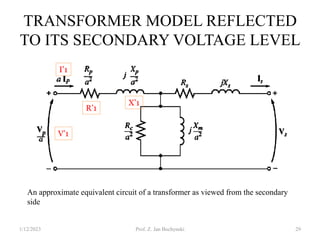
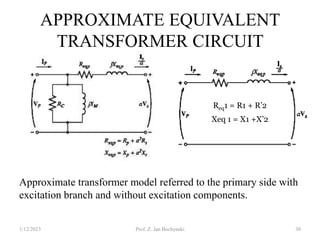
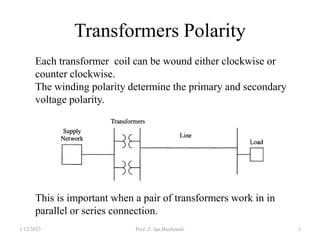
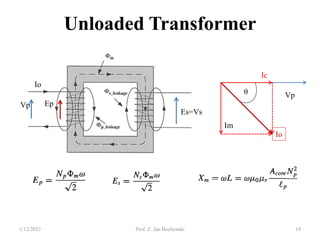
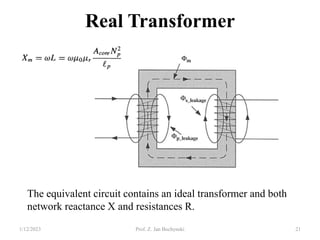
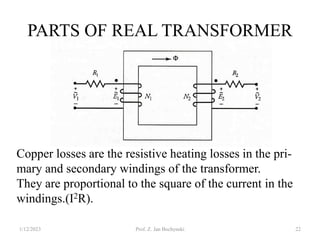
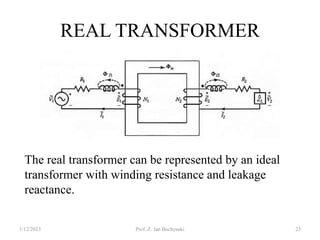
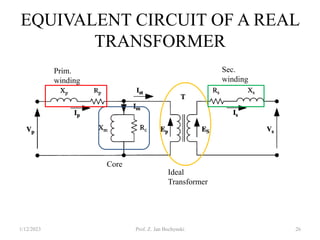
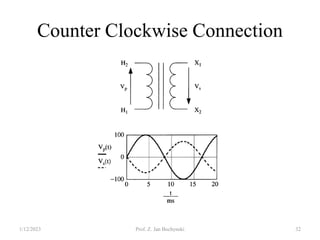
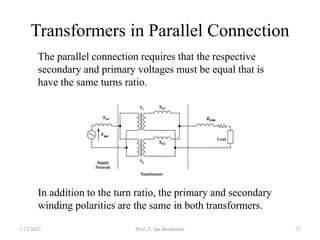
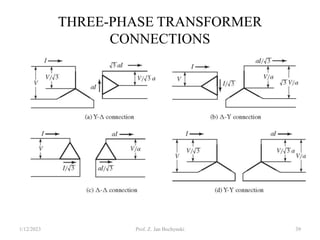
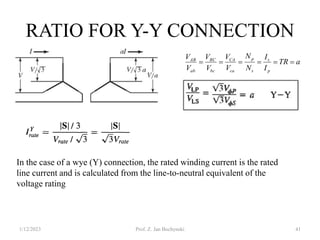
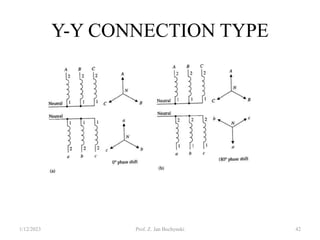
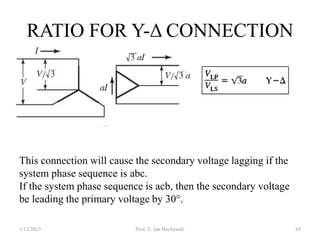
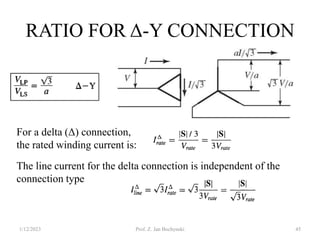
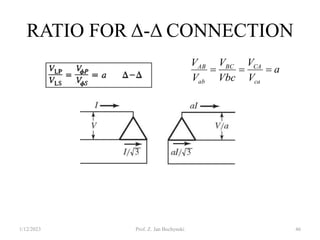
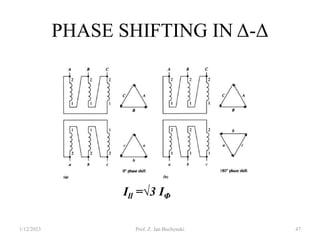
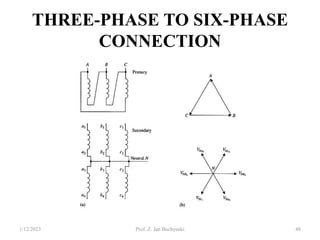
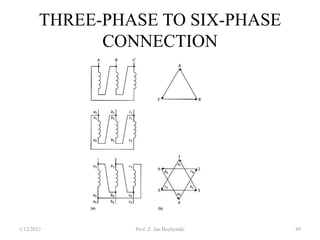
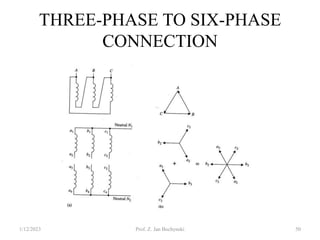
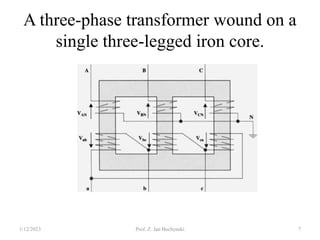
- Transformers allow the transfer of power between circuits at different voltage levels through electromagnetic induction. They work by changing the voltage and current in opposite proportions while keeping power constant. - An ideal transformer has no losses, but a real transformer is modeled with winding resistances and leakage reactances to account for energy losses. - Transformers can be connected in various configurations depending on the application, including wye-wye, wye-delta, delta-delta, etc. Proper transformer selection and connection is important for voltage regulation and power transmission efficiency.

1. TRANSFORMERS
FUNDAMENTALS
NYU EE 3824 ENERGY
CONVERSION SYSTEMS
INSTRUCTOR Prof. Z. Jan Bochynski
1/12/2023 Prof. Z. Jan Bochynski 1

2. Transformers in a Power Grid
An important safety feature is that the transformer insulates the primary and
secondary electric circuits and permits the separate grounding of the circuits, which
prevents high-voltage, high-power damage the secondary circuit.
Limit 20-26 kV
1/12/2023 Prof. Z. Jan Bochynski 2

3. Transformers Polarity
Each transformer coil can be wound either clockwise or
counter clockwise.
The winding polarity determine the primary and secondary
voltage polarity.
This is important when a pair of transformers work in in
parallel or series connection.
1/12/2023 Prof. Z. Jan Bochynski 3

4. THREE-PHASE TRANSFORMERS
1/12/2023 Prof. Z. Jan Bochynski 4

5. Large oil-cooled high-voltage
transformer
1/12/2023 Prof. Z. Jan Bochynski 5

6. Three-phase Transformer
1/12/2023 Prof. Z. Jan Bochynski 6

7. A three-phase transformer wound on a
single three-legged iron core.
1/12/2023 Prof. Z. Jan Bochynski 7

8. Transformers in Electronics
1/12/2023 Prof. Z. Jan Bochynski 8
Transformer allows matching impedance to obtain a maximum
power in electronic devices
Transformers allows electrical isolation between systems

9. TRANSFORMER PROPERTIES
1/12/2023 Prof. Z. Jan Bochynski 9
Transformer works only when a magnetic flux changes
Transformer does not convert energy
Transformer transmits power from one network to another
Transformer increasing voltage decreasing current and vice
versa
Transformer allows phase conversion in secondary circuit

10. Transformer Lamination
1/12/2023 Prof. Z. Jan Bochynski 10

11. Transformer Core Type
Construction
Iron core magnetic circuit
1/12/2023 Prof. Z. Jan Bochynski 11

12. Transformer Winding
1/12/2023 Prof. Z. Jan Bochynski 12

13. Transformer Construction
1/12/2023 Prof. Z. Jan Bochynski 13

14. Transformer Shell Type
Construction
Iron core magnetic circuit with an air gap
1/12/2023 Prof. Z. Jan Bochynski 14

15. H1
H2
X1
X2
Transformer Ratio
Transformer turns ratio
Ns
Np
Es
Ep

Ns
Np
Es
Ep

1/12/2023 Prof. Z. Jan Bochynski 15
Φ
Es = Ep (Ns /Np)
The secondary (output voltage )

16. Power, Currents, Voltage, Flux
1/12/2023 Prof. Z. Jan Bochynski 16
]
[
44
.
4
4
11
.
1 V
N
f
N
f
E m
m
rms 








17. IDEAL TRANSFORMER
1/12/2023 Prof. Z. Jan Bochynski 17

m 
E1
4.44 fN1

TR  a 
e1
e2

N1
N2

i2
i1

18. Ideal Transformer
Es = Ns ΔФ / Δt
Ep = Np ΔФ /Δt
1/12/2023 Prof. Z. Jan Bochynski 18

19. Unloaded Transformer
Vp
Ic
Im
Io
θ
Io
Vp Ep
Es=Vs
1/12/2023 Prof. Z. Jan Bochynski 19

20. NO-LOAD CURRENTS
1/12/2023 Prof. Z. Jan Bochynski 20
Iex
Ic = Ih+e VP
Im
Φ
The magnetization current Im is the current required to produce the
flux Φ in the transformer core.
The core-loss current Ih+e is the current required to make up for
hysteresis and eddy current losses
The fundamental component of the magnetization current lags the
voltage applied to the core by 90°.
The total no-load current in the core is called the excitation current of the
transformer. This current is the sum of the magnetization current and the core-
loss current in the core:
Iex = Im + Ih+e

21. Real Transformer
The equivalent circuit contains an ideal transformer and both
network reactance X and resistances R.
1/12/2023 Prof. Z. Jan Bochynski 21

22. PARTS OF REAL TRANSFORMER
1/12/2023 Prof. Z. Jan Bochynski 22
Copper losses are the resistive heating losses in the pri-
mary and secondary windings of the transformer.
They are proportional to the square of the current in the
windings.(I2R).

23. REAL TRANSFORMER
1/12/2023 Prof. Z. Jan Bochynski 23
The real transformer can be represented by an ideal
transformer with winding resistance and leakage
reactance.

24. Loaded Transformer
Ns
Np
Is
Ip 

1/12/2023 Prof. Z. Jan Bochynski 24

25. LEAKAGE FLUXES
1/12/2023 Prof. Z. Jan Bochynski 25
The leakage fluxes ΦLP and ΦLS
are fluxes that escape the core and
pass through only one of the
transformer windings. They
produce a self-inductance L in the
primary and secondary coils, and
the effects of this inductance must
be accounted in calculation.
Φs = ΦM + ΦLS
ΦP = ΦM + ΦLS

26. EQUIVALENT CIRCUIT OF A REAL
TRANSFORMER
1/12/2023 Prof. Z. Jan Bochynski 26
Ideal
Transformer
Sec.
winding
Prim.
winding
Core

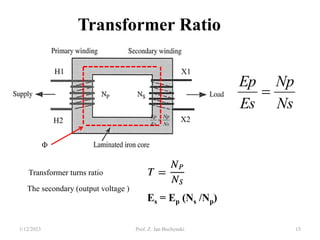
27. Real Transformer Equivalent Circuit
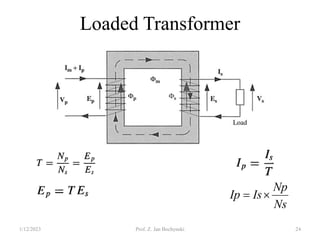
Ep =4.44 Фm f Np [V]
Es = 4.44 Фm f Ns [V]
Ф (Wb), f (Hz)
Ep = Vp + ΔVp = Vp + (IoRp + Io Xp )
Vp = Ep - ΔVp = Ep + (IoRp + Io Xp )
1/12/2023 Prof. Z. Jan Bochynski 27

28. TRANSFORMER MODEL REFERRED
TO ITS PRIMARY VOLTAGE LEVEL
1/12/2023 Prof. Z. Jan Bochynski 28
Approximate equivalent circuit of a transformer as viewed
from the primary side
R’2 X’2
I’2
V’2

29. TRANSFORMER MODEL REFLECTED
TO ITS SECONDARY VOLTAGE LEVEL
1/12/2023 Prof. Z. Jan Bochynski 29
An approximate equivalent circuit of a transformer as viewed from the secondary
side
R’1
X’1
I’1
V’1

30. APPROXIMATE EQUIVALENT
TRANSFORMER CIRCUIT
1/12/2023 Prof. Z. Jan Bochynski 30
Approximate transformer model referred to the primary side with
excitation branch and without excitation components.
Req1 = R1 + R’2
Xeq 1 = X1 +X’2

31. Clockwise Connection
1/12/2023 Prof. Z. Jan Bochynski 31

32. Counter Clockwise Connection
1/12/2023 Prof. Z. Jan Bochynski 32

33. Transformer with Center -Tapped
Secondary Windings
1/12/2023 Prof. Z. Jan Bochynski 33

34. Two Secondary Windings Transformer
Secondary winding connected in series – aiding voltage
1/12/2023 Prof. Z. Jan Bochynski 34

35. Two Secondary Winding Transformer
Secondary winding connected in series – opposing voltage
1/12/2023 Prof. Z. Jan Bochynski 35

36. Multi-output Transformers
1/12/2023 Prof. Z. Jan Bochynski 36

37. Transformers in Parallel Connection
In addition to the turn ratio, the primary and secondary
winding polarities are the same in both transformers.
The parallel connection requires that the respective
secondary and primary voltages must be equal that is
have the same turns ratio.
1/12/2023 Prof. Z. Jan Bochynski 37

38. CONDITIONS FOR
TRANSFORMERS IN PARALLEL
1/12/2023 Prof. Z. Jan Bochynski 38
The condition for connecting two transformers in parallel:
1. Two transformers must the same turns ratios
2. The nominal voltage and current ratings must be the same
3. The equivalent resistance, reactance, and impedance must be
the same
4. The polarities must be the same
5. Two transformers must have the same construction of core or
shell type.

39. THREE-PHASE TRANSFORMER
CONNECTIONS
1/12/2023 Prof. Z. Jan Bochynski 39

40. TRANSFORMERS CONNECTIONS
1/12/2023 Prof. Z. Jan Bochynski 40
wye-wye (Y-Y) Seldom used, unbalanced and 3rd harmonics problems
wye-wye-delta (Y-Y-Δ)
Frequently is used to interconnect high voltage networks
(240 kV/345 kV). The delta winding filters the 3rd
harmonics, equalizes the unbalanced current, and
provides a path for ground current
wye-delta (Y-Δ) Frequently is used as step down (345 kV/69 kV)
delta-delta (Δ-Δ)
Used for medium voltage (15 kV), one of the
transformers can be removed (open delta)
delta-wye (Δ-Y) Step-up transformer in a generation station

41. RATIO FOR Y-Y CONNECTION
1/12/2023 Prof. Z. Jan Bochynski 41
In the case of a wye (Y) connection, the rated winding current is the rated
line current and is calculated from the line-to-neutral equivalent of the
voltage rating
a
TR
I
I
N
N
V
V
V
V
V
V
p
s
s
p
ca
CA
bc
BC
ab
AB







42. Y-Y CONNECTION TYPE
1/12/2023 Prof. Z. Jan Bochynski 42

43. RATIO FOR Y-Δ CONNECTION
1/12/2023 Prof. Z. Jan Bochynski 43
This connection will cause the secondary voltage lagging if the
system phase sequence is abc.
If the system phase sequence is acb, then the secondary voltage
be leading the primary voltage by 30°.

44. PHASE SHIFTING IN Y-Δ
1/12/2023 Prof. Z. Jan Bochynski 44
l
l
l
l
l
l
l
l
V
V
V
V
V
/
V
V
V
V
V
a
2
2
2
1
2
1
3
3
3









VΦ = Vll /√3
3
a
V
V
ab
AB


45. RATIO FOR Δ-Y CONNECTION
1/12/2023 Prof. Z. Jan Bochynski 45
For a delta (Δ) connection,
the rated winding current is:
The line current for the delta connection is independent of the
connection type

46. RATIO FOR Δ-Δ CONNECTION
1/12/2023 Prof. Z. Jan Bochynski 46
a
V
V
Vbc
V
V
V
ca
CA
BC
ab
AB




47. PHASE SHIFTING IN Δ-Δ
1/12/2023 Prof. Z. Jan Bochynski 47
Ill =√3 IΦ

48. THREE-PHASE TO SIX-PHASE
CONNECTION
1/12/2023 Prof. Z. Jan Bochynski 48

49. THREE-PHASE TO SIX-PHASE
CONNECTION
1/12/2023 Prof. Z. Jan Bochynski 49

50. THREE-PHASE TO SIX-PHASE
CONNECTION
1/12/2023 Prof. Z. Jan Bochynski 50

51. Examples
1/12/2023 Prof. Z. Jan Bochynski 51

52. Example 1
The transformer has alternating input
of 100 V. The number of turns on
each winding are NP = 375, NS1 =
750, NS2 = 500, NS3 = 75.
1. Determine the output voltage from
each secondary winding.
2. Find the total output if all of three
secondary windings were connected in
series-adding.
1/12/2023 Prof. Z. Jan Bochynski 52

53. Solution
Example 1
1/12/2023 Prof. Z. Jan Bochynski 53

54. EXAMPLE 2
The three secondary in Problem 1 have following loads
attached: RS1 =1 kΩ, RS2 = 500 Ω, and RS3 = 100 Ω.
Assuming that the transformer is 100 % efficient find
the total primary current Ip.
1/12/2023 Prof. Z. Jan Bochynski 54

55. Solution Example 2
For the secondary winding in coil 1 current is
Is1 =Es1/Rs1 = 200V/1kV = 200 mA
Ip =Is x Ns / Np
Ip1 =Is1 x Ns1 / Np = 200 mA x (750/375 ) = 400 mA
1/12/2023 Prof. Z. Jan Bochynski 55

56. Example 3
The transformer input max voltage is 100 V, frequency 400 Hz
and the primary winding has 375 turns.
Determine the pick value of the flux Φ.
1/12/2023 Prof. Z. Jan Bochynski 56

57. Solution Example 3
Wb
Wb
Hz
V
N
f
E
p
p
m

150
10
150
375
400
44
.
4
100
44
.
4
6












1/12/2023 Prof. Z. Jan Bochynski 57

58. Example 4
1/12/2023 Prof. Z. Jan Bochynski 58
A transformer with two secondary windings has these turns
data: N1 = 4000, N2 = 1000, N3 = 500. The primary rms
voltage is 120 V. The secondary voltage is V2 = 30<00 and
V3 = 15<00. The secondary windings loads are: Z2 = 3 +j 4;
and Z3 = 5 +j 0.
Compute the followings:
1. Current in all three windings
2. Active power in the primary circuit
3. Apparent power in the primary winding
4. Reactive power in the primary winding
5. Power factor of the system

59. 1/12/2023 Prof. Z. Jan Bochynski 59
Solution Example 4
I2 = E2/Z2 = 30<00 / (3+j4) = 6<-53.10 A
I3 = E3/Z3 = 15<00 / (5+j00) = 3<00 A
Since the primary power is equal to the secondary power
I1 x N1 = I2 x N2 + I3 x N3
I1 x 4000 =(6<-53.10) x 1000 + 3 x 500
I1 = 1.276 – j 1.2 =1.75<-43.260 A
Apparent power of the source is
S1 = E1 x I1* = (120<00) (1.75<+43.260) = 153 + j 144 VA
Active power P = 153 W
Reactive power Q = 144 VAR
P.F. = cos 43.260 = 0.728 leading