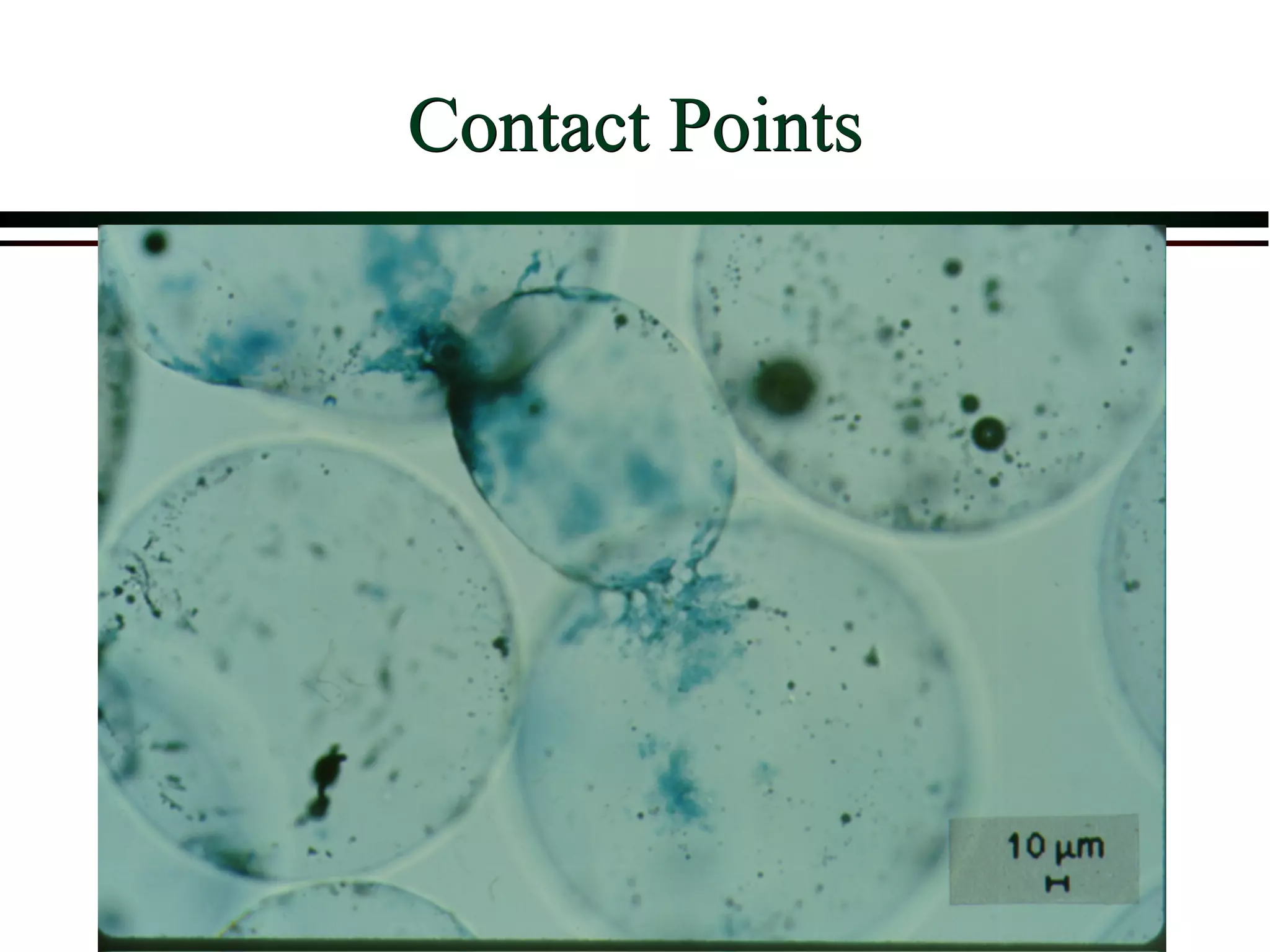
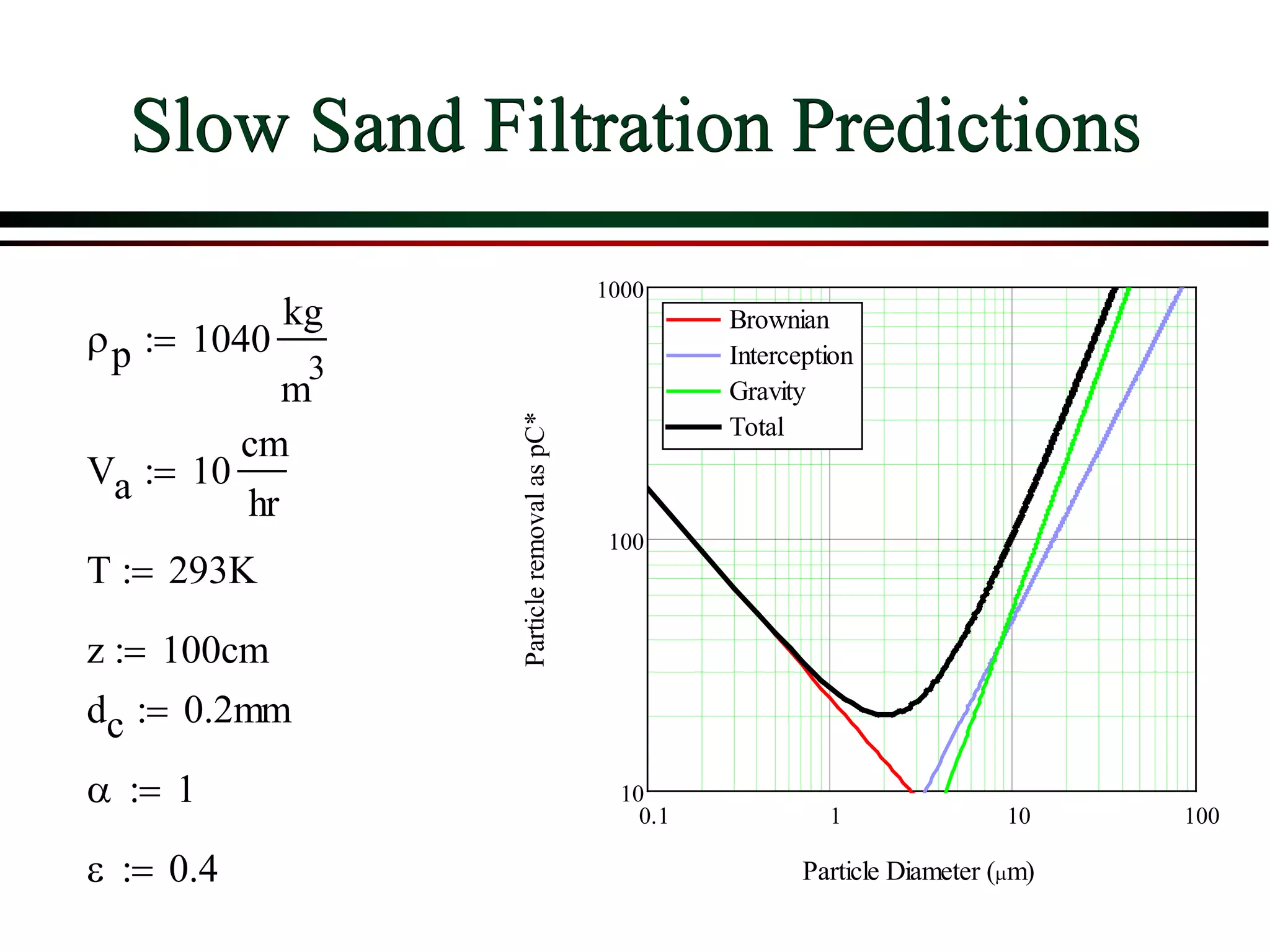
This document provides an overview of filtration theory and processes. It defines filtration as the removal of solids suspended in a liquid by passing the liquid through a porous medium that retains the solids. Various filter types and operating mechanisms are described, including depth filtration, cake filtration, and clarification. Key factors that affect filtration rates such as pressure, viscosity, permeability, and particle size are also discussed. Dimensionless parameters important to modeling filtration like the Reynolds number are introduced.

2. FILTRATION
FILTRATION

3. FILTRATION
Filtration Theory
On removing little particles
with big particles

4. Filters Galore
“Bio” Sand
Rapid Sand
Cartridge
Bag
Pot
Candle
Diatomaceous earth filter
Slow Sand
Rough

5. Introduction
Filtration by description is a process by which
suspended solid particles in a liquid medium are
separated from that liquid by passing the liquid
through a porous, medium (e.g., a sand bed) capable
of entrapping the suspended particles.
A pressure gradient generated across the filter bed is
the driving force for filtration to take place.

6. Introduction continued
 There is to some extent an overlapping description of
filtration and sedimentation during separation process.
 However the two processes (filtration and sedimentation)
work by quite different mechanisms.
 Filtration operates entirely on particle or droplet size (and,
to some extent, shape), such that particles below a certain
size will pass through the barrier, while larger particles are
retained on or in the barrier for later removal.
 The separating size is a characteristic of the barrier, the
filter medium

7. Introduction continued
 Sedimentation, on the other hand, operates on the density of the
particle or droplet, or, more correctly, on the density difference
between the suspended particle and the suspending fluid.
 It is the force of gravity working on this density difference (or the
much higher centrifugal force operating in a centrifuge) that causes
separation by sedimentation – either of a solid from its suspension, or
of a lighter solid from a heavier one.
 Particle size also has a part to play in sedimentation – a larger particle
will settle faster than a smaller one, of the same density.
 This topic will be discussed in details later.

8. What is FILTRATION??
• As alluded earlier, this may be defined as the removal of
solids, suspended in a fluid, by passage through a porous
medium on or in which the solids are retained.
• If the recovery of the solids is desired the operation is
termed cake filtration.
• If recovery of the solids is not important but a particle free
fluid required, the operation is termed clarification.
• In the latter process, the concentration of solids do not
usually exceed 1%.

9. Pressure Gradient Generation in
Filtration Operations
The pressure gradient in filtration can be
produced in a variety of ways including:
• Gravity
• Vacuum
• high pressure
• centrifugal forces

10. Classification of Solid-Liquid
Separation Processes
Solid-Liquid Separation Processes
Using Density Using Pressure Gradient
As a Driving Force As a Driving Force
Sedimentation Flotation Centrifugation Deep-Bed Cake Cross Flow
Thickening Filtration Filtration Filtration
Fixed Wall Rotating Wall
Centrifugation Centrifugation

11. Filter Medium
The filter medium is the element that produces
the filtering action. Examples include:
• filter screens and supporting septa (e.g., a fabric
screen);
• beds of particulate materials (e.g., sand, coal);
• beds of solids screened from the solid-liquid
suspension (e.g., biosolids in sludge thickening) or a
slurry (e.g., diatomaceous earth).

12. Types of Filtration Operations
 Cross-flow filtration, in which a septum is responsible for
the filtering action (e.g., microscreens);
 Depth (or deep-bed) filtration, in which the particles are
removed throughout the filter bed or in a significant portion
of it (e.g. sand filters);
 Cake filtration, in which the particles are removed on the
surface of a cake formed by the solids accumulating on a
septum (e.g., rotary vacuum filters).

13. Classification of Filtration
Systems
 Filtration systems can be classified according to:
• type of operation (batch vs. continuous)
• direction of fluid flow with respect of filter medium
(perpendicular vs. parallel)
• type of filter medium (e.g., screen, deep bed, cake)
• location within the filter medium where particle deposition
occurs
• flow rate or pressure control during filtration (e.g., constant
pressure drop)

14. Filtration Operations
 Batch or semicontinuous filtration
• Periodical removal of solids is required (e.g., through
backwashing)
• Pressure across and/or flow rate through filter change with
time
 Continuous filtration
• Solids are continuously removed
• Pressure across and/or flow rate through filter are relatively
constant with time

15. Clarification
 This may be achieved by surface filtration or by
depth filtration.
 In surface filtration the pore size of the filter
determines the size of particles passing through or
being retained. The life of such filters depends on the
number of pores available for passage of the fluid.
 Once a particle is trapped at the entrance to a pore
then that pore is unavailable for transport of fluid.

16. Clarification(CONTINUE)
 In depth filtration the particles are very much
smaller than the pore size of the filter.
 Because of this, the filters must be of sufficient
depth that even the smallest particle in a slurry
will pass through the filter.
 Clarification may be carried out by the use of
thick media which allows the arrest of particles by
entrapment, impingement and electrostatic effects.

17. Cake Filtration
 In this case, recovery of the solids is also
important.
 Generally the solids form a cake on the surface of
the medium and the clarified liquid is discharged
from the filter.
 The actual filtration is carried out by the cake of
solids themselves.
 In such cases the solids may completely penetrate
the septum until deposition of an effective cake
occurs.
 Until this time cloudy filtrate may be recycled.

18. Process Variables Affecting
Filtration
Flow rate of slurry
Type of slurry and solid particles contained in it
• Liquid viscosity
• Liquid density
• Solid concentration
• Particle size distribution
• Surface charge of particles
• Type and/or shape or particles

19. Process Variables Continued
 Type and properties of filter medium
• Medium average particle size and shape
• Medium particle size distribution
• Medium surface charge
• Medium density
• Medium void fraction (porosity)
• Mesh size opening
 Height of filter medium
 Allowable pressure drop across filter

20. Particle Removal Mechanisms
Involved in Filtration
 Mechanical straining
 Sedimentation on filter medium
 Impaction with filter medium
 Interception by contact with filter medium
 Flocculation
 Adhesion / adsorption
• Chemical adsorption
• Physical adsorption

21. What is then the
Theory of Filtration??
 Flow of fluids through a porous medium
 Some solid material is retained either on the surface or adsorbed within the material matrix of
the filter bed
 The filtrate continues to the collection vessel
 This can be described by the following equation:
Q = B x PA
Z L
Where Q is the volumetric flow rate, A is the area of the filter bed, L is the thickness, P is the
pressure difference across the bed causing flow, Z is the viscosity of the fluid and B is the
permeability coefficient. The permeability coefficient may be related to the
 powder properties of the bed by the equation:
B = E³/5(1-E)² S○²
Where E is the porosity of the bed and S○ is the specific surface area.

22. Factors affecting filtration rate
Any factor which affects one of the terms on the right hand side of
the above equation will affect the filtration rate.
 Pressure:
- In cake filtration, deposition of solids over a finite period
increases the bed depth (L).
- If the pressure remains constant the rate of filtration will
decrease.
- In pressure filtration it is usual to employ a low initial pressure
which is progressively increased as filtration proceeds.
- In this way, the rate of filtration is held constant.

23. Factors (continued)
 Viscosity
- Higher pressures are required for maintaining
a given flow rate of a thick liquid than for
maintaining the same flow rate of a less viscous
liquid.
- In some operations hot filtration is employed to
reduce the viscosity of the slurry.

24. Factors (continued)
 Permeability Coefficient
- The permeability coefficient may be explained in terms of its
two variables, E and S
- When filtering a slurry, the porosity of the cake depends on the
way in which the particles are deposited or packed.
- A fast rate of deposition, given by concentrated slurries or
higher flow rates may give a cake of higher porosity.
- Alternatively, a broad particle size distribution may reduce the
porosity of the cake because particles will tend to separate on
deposition, thus reducing even packing of particles.
 In clarification, high permeability and filtration rate oppose
good particle retention.

25. Factors (continued)
 The remainder of the energy is lost as: -
- Elastic deformation of particles.
- Transport of material in the milling chamber.
- Friction between the particles.
- Friction between the particles and the mill.
- Heat.
- Vibration and noise.
• A number of empirical equations have, however, been
proposed such as:

26. Factors (continued)
• In a depth filter, the path followed by the liquid
through the filter is tortuous.
• Changes in direction and velocity (tortuisity) occur
as the liquid passes through the pore system of the
filter.
• Increase in velocity decreases the opportunity for
contact and retention of the particles by the medium

27. Factors (continued)
• The rate of filtration is found to be inversely
proportional to the resistance of the solids
cake.
• Slurry, gelatinous or highly compressible
materials form impermeable cakes with
high resistance to liquid flow.
• Filter aids generally reduce this resistance.

28. Categorizing Filters
 Straining
Particles to be removed are larger than the pore size
Clog rapidly
 Depth Filtration
Particles to be removed may be much smaller than the
pore size
Require attachment
Can handle more solids before developing excessive
head loss
Filtration model coming…
All filters remove more particles near the filter inlet

29. The “if it is dirty, filter it” Myth
The common misconception is that if the
water is dirty then you should filter it to
clean it
But filters can’t handle very dirty water
without clogging quickly

30. Developing a Filtration Model
Iwasaki (1937) developed relationships describing
the performance of deep bed filters.
0=
dC
C
dz
λ−
C is the particle concentration [number/L3]
λ0 is the initial filter coefficient [1/L]
z is the media depth [L]
The particle’s chances of being caught are the same at
all depths in the filter; pC* is proportional to depth
0=
dC
dz
C
λ−
0
0
0
=
C z
C
dC
dz
C
λ−∫ ∫ 0
0
ln =
C
z
C
λ
 
−  
 
( ) 0
0
1
log *
ln 10
C
pC z
C
λ
 
− = = 
 
0
*
C
C
C
=

31. Graphing Filter Performance
1 2 3 4
0.2
0.4
0.6
0.8
1
Removed
t
1 2 3 4
0
0.2
0.4
0.6
0.8
1
p Remaining( )
t
p x( ) log x( )−:=
This graph gives the
impression that you can
reach 100% removal 1 2 3 4
0
1
2
p Remaining( )
t
Where is 99.9% removal?

32. Particle Removal Mechanisms in
Filters
Transport to a surface depends on
Attachment
Molecular diffusion
Inertia
Gravity
Interception
Straining
London van der Waals
collector

33. Filtration Performance: Dimensional
Analysis
What is the parameter we are interested in
measuring or determining filtration?
_________________
How could we make performance
dimensionless? ____________
What are the important forces?
Effluent concentration
C/C0 or pC*
Inertia London van der Waals Electrostatic
Viscous
Need to create dimensionless force ratios!
Gravitational Thermal

34. Dimensionless Force Ratios
Reynolds Number
Froude Number
Weber Number
Mach Number
 Pressure/Drag Coefficients
 (dependent parameters that we measure experimentally)
Re
Vlr
m
=
Fr
V
gl
=
( )
2
2
Cp
p
Vr
- D
=
σ
ρlV
W
2
=
c
V
M =
AV
d
2
Drag2
C
ρ
=
2
fu
V
l
m=
fg gr=
2
f
l
s
s
=
2
f vE
c
l
r
=
2
fi
V
l
r=
( )p g zrD + D

35. What is the Reynolds number for
filtration flow?
 What are the possible length scales?
• Void size (collector size) max of 0.7 mm in RSF
• Particle size
 Velocities
• V0 varies between 0.1 m/hr (SSF) and 10 m/hr (RSF)
 Take the largest length scale and highest velocity to
find max Re
 For particle transport the length scale is the particle
size and that is much smaller than the collector size
( )3
2
6
10 0.7 10
3600
Re 2
10
m hr
m
hr s
m
s
−
−
 
× 
 = =
 
 
 
Re
Vl
ν
=

36. Choose viscosity!
In Fluid Mechanics inertia is a significant “force”
for most problems
In porous media filtration viscosity is more
important than inertia.
We will use viscosity as the repeating parameter
and get a different set of dimensionless force ratios
Inertia
Gravitational
Viscous
Thermal
Viscous

37. Gravity
2
g
0
( )
=
18
p w pgd
V
ρ ρ
µ
−
Π
2
g
( )
=
18
p w pgd
v
ρ ρ
µ
−
vpore
g
0
=
gv
V
Π
Gravity only helps when
the streamline has a
_________ component.horizontal
2
fu
V
l
µ=
fg gr=
g =
gf
fµ
Π
g
0
2
=
p
g
V
d
ρ
µ
∆
Π
2
g
0
( )
=
p w pgd
V
ρ ρ
µ
−
Π
velocities forces
Use this definition

38. Diffusion (Brownian Motion)
kB=1.38 x 10-23 J/°K
T = absolute temperature
vpore
Br
03
B
p c
k T
d V dπµ
Π =
3
B
p
k T
D
dπµ
=
2
L
T
 
 
 
d
c
D
v
d
∝
dc is diameter of the collector
Diffusion velocity is
high when the particle
diameter is ________.small

39. London van der Waals
The London Group is a measure of the
attractive force
It is only effective at extremely short range
(less than 1 nm) and thus is NOT
responsible for transport to the collector
H is the Hamaker’s constant

Lo 2
p 0
4H
=
9 d Vπµ
Π
20
= 0.75 10H J−
×
Van der Waals force
Viscous force

40. What about Electrostatic
repulsion/attraction?
Modelers have not succeeded in describing
filter performance when electrostatic
repulsion is significant
Models tend to predict no particle removal
if electrostatic repulsion is significant.
Electrostatic repulsion/attraction is only
effective at very short distances and thus is
involved in attachment, not transport

41. Geometric Parameters
What are the length scales that are related to particle
capture by a filter?
 ______________
 __________________________
 ______________
 Porosity (void volume/filter volume) (ε)
Create dimensionless groups
Choose the repeating length ________
Filter depth (z)
Collector diameter (media size) (dc)
Particle diameter (dp)
p
R
c
d
d
Π = z
c
z
d
Π =
(dc)
Number of collectors! Π.z
3 1 ε−( )⋅
2 ln 10( )⋅
z
d.c






⋅:=
Definition used in model

42. Write the functional relationship
( ),g Br* , , ,R zpC f ε= Π Π Π Π
( ),g Br* , ,z RpC f ε=Π Π Π Π
If we double depth of filter what does pC* do? ___________doubles
How do we get more detail on this functional relationship?
Empirical measurements
Numerical models

43. Numerical Models
Trajectory analysis
A series of modeling attempts with
refinements over the past decades
Began with a “single collector” model that
modeled London and electrostatic forces as
an attachment efficiency term (α)
( ), ,g Br* ,z RpC f ε=Π Π Π Π α

44. Filtration Model
γ ε( ) 1 ε−( )
1
3
:=
A.s ε( ) 2 1 γ ε( )5
−( )⋅
2 3 γ ε( )⋅− 3 γ ε( )5
⋅+ 2 γ ε( )6
⋅−
:=
Π.g d.p( )
d.p
2
ρ.p ρ.w−( )⋅ g⋅
18 µ⋅ V.a⋅
:=
Π.R d.p( )
d.p
d.c
:=
Π.z
3 1 ε−( )⋅
2 ln 10( )⋅
z
d.c






⋅:=
Π.Br d.p( )
k.b T⋅
3 π⋅ µ⋅ d.p⋅ V.a⋅ d.c⋅
:=
Porosity
Geometry
Force ratios

45. Transport Equations
ηBr dp( )
3
4
As ε( )
1
3
⋅ ΠR dp( )
1
6
−
⋅ ΠBr dp( )
2
3
⋅:=
ηR dp( )
1
21.5
As ε( )⋅ ΠR dp( )
1.425
⋅:=
ηg dp( ) 0.31 Πg dp( )⋅:=
η dp( ) ηBr dp( ) ηR dp( )+ ηg dp( )+:=
pC d.p( ) Π.z α⋅ η d.p( )⋅:=
Brownian motion
Interception
Gravity
Total is sum of parts
Transport is additive

46. Filtration Technologies
 Slow (Filters→English→Slow sand→“Biosand”)
First filters used for municipal water treatment
However, these were unable to treat the turbid waters of the Ohio
and Mississippi Rivers effectively
Can be used after Roughening the filters
 Rapid (Mechanical→American→Rapid sand)
Used in Conventional Water Treatment Facilities
Used after coagulation/flocculation/sedimentation
High flow rates→clog daily→hydraulic cleaning
 Ceramic are usually used for commercial filtering
processes.

47. Rapid Sand Filter
(Conventional US Treatment)
Sand
Gravel
Influent
Drain
Effluent Wash water
Anthracite
Size
(mm)
0.70
0.45 - 0.55
5 - 60
Specific
Gravity
1.6
2.65
2.65
Depth
(cm)
30
45
45

48. Filter Design
 Filter media
silica sand and anthracite coal
non-uniform media will stratify with _______ particles
at the top
 Flow rates
60 - 240 m/day
 Backwash rates
set to obtain a bed porosity of 0.65 to 0.70
typically 1200 m/day
smaller
Compare with sedimentation

49. Sand
Gravel
Influent
Drain
Effluent Wash water
Anthracite
Backwash
Wash water is
treated water!
WHY?
Only clean water
should ever be on
bottom of filter!

50. 0.1 1 10 100
0.1
1
10
100
Brownian
Interception
Gravity
Total
Particle Diameter (µm)
ParticleremovalaspC*
Rapid Sand predicted performance
ρp 1040
kg
m
3
:=
Va 5
m
hr
:=
T 293K:=
z 45cm:=
dc 0.45mm:=
α 1:=
ε 0.4:=
Not very good at removing particles that
haven’t been flocculated

51. Slow Sand Filtration
 First filters to be used on a widespread basis
 Fine sand with an effective size of 0.2 mm
 Low flow rates (2.5-10 m/day)
 Schmutzdecke (_____ ____) forms on top of the
filter
causes high head loss
must be removed periodically
 Used without coagulation/flocculation!
 Turbidity should always be less than 50 NTU with
a much lower average to prevent rapid clogging
filter cake
Compare with sedimentation

52. Slow Sand Filtration Mechanisms
Protozoan predators (only
effective for bacteria removal,
not virus or protozoan removal)
Aluminum (natural sticky
coatings)
Attachment to previously
removed particles
No evidence of removal by
biofilms

53. Typical Performance of SSF Fed
Cayuga Lake Water
0.05
0.1
1
0 1 2 3 4 5
Time (days)
FractionofinfluentE.coli
remainingintheeffluent
Filter performance doesn’t improve if the filter
only receives distilled water
(Daily samples)

54. Particle Removal by Size
0.001
0.01
0.1
1
0.8 1 10Particle diameter (µm)
control
3 mM azide
Fractionofinfluentparticles
remainingintheeffluent
Effect of
the Chrysophyte
What is the physical-
chemical mechanism?

55. Techniques to Increase Particle
Attachment Efficiency
Make the particles stickier
The technique used in conventional water
treatment plants
Control coagulant dose and other coagulant aids
(cationic polymers)
Make the filter media stickier
Biofilms in slow sand filters?
Mystery sticky agent present in surface waters
that is imported into slow sand filters?

56. Cayuga Lake Seston Extract
Concentrate particles from Cayuga Lake
Acidify with 1 N HCl
Centrifuge
Centrate contains polymer
Neutralize to form flocs

57. Seston Extract Analysis
11%
13%
17%
56%
volatile solids
Al
Na
Fe
P
S
Si
Ca
other metals
other nonvolatile solids
How much Aluminum should be added to a filter?
carbon
16%
I discovered
aluminum!

58. 0
1
2
3
4
5
6
7
0 2 4 6 8 10
time (days)
E.coliremaining(pC*
control
4
20
100
end azide
Horizontal bars
indicate when
polymer feed was
operational for each
filter.
E. coli Removal as a Function of
Time and Al Application Rate
pC* is proportional to accumulated mass of Aluminum in filter
2
mmol Al
m day⋅
No E. coli detected20 cm deep filter columns

59. Slow Sand Filtration Predictions
ρp 1040
kg
m
3
:=
Va 10
cm
hr
:=
T 293K:=
z 100cm:=
dc 0.2mm:=
α 1:=
ε 0.4:=
0.1 1 10 100
10
100
1000
Brownian
Interception
Gravity
Total
Particle Diameter (µm)
ParticleremovalaspC*

60. How deep must a filter (SSF) be to
remove 99.9999% of bacteria?
 Assume α is 1 and dc is
0.2 mm, V0 = 10 cm/hr
 pC* is ____
 z is ________________
 What does this mean?
23 cm for pC* of 6
6
Suggests that the 20 cm deep experimental filter
was operating at theoretical limit
pC 1µm( ) 25.709= for z of 1 m
Typical SSF performance is 95% bacteria removal
Only about 5 cm of the filters are doing anything!

61. Head Loss Produced by Aluminum
0
0.2
0.4
0.6
0.8
1
0 50 100 150
Total Al applied
headloss(m)
3.9
20 2
mmol Al
m day⋅
2
mmol Al
m

62. Aluminum feed methods
Alum must be dissolved until it is blended
with the main filter feed above the filter
column
Alum flocs are ineffective at enhancing
filter performance
The diffusion dilemma (alum microflocs
will diffuse efficiently and be removed at
the top of the filter)
0.1 1 10
1
10
100
particle diameter
ParticleremovalaspC*
pCPe dp( )
pCR dp( )
pCg dp( )
pC dp( )
dp
µm

63. Performance Deterioration after Al
feed stops?
Hypotheses
Decays with time
Sites are used up
Washes out of filter
Research results
Not yet clear which
mechanism is
responsible – further
testing required
0
1
2
3
4
5
6
7
0 2 4 6 8 10
time (days)
E.coliremaining(pC*)
control
4
20
100
end azide
Horizontalbars
indicate when
polymer feed was
operationalfor each

64. Sticky Media vs. Sticky Particles
 Sticky Media
Potentially treat filter
media at the beginning
of each filter run
No need to add
coagulants to water for
low turbidity waters
Filter will capture
particles much more
efficiently
 Sticky Particles
Easier to add coagulant
to water than to coat
the filter media

65. The BioSand Filter Craze
 Patented “new idea” of slow sand filtration
without flow control and called it “BioSand”
 Filters are being installed around the world as
Point of Use treatment devices
 Cost is somewhere between $25 and $150 per
household ($13/person based on project near
Copan Ruins, Honduras)
 The per person cost is comparable to the cost to
build centralized treatment using the AguaClara
model

66. “BioSand” Performance

67. “BioSand” Performance
Pore volume is 18 Liters
Volume of a bucket is ____________
Highly variable field performance even
after initial ripening period
http://www.iwaponline.com/wst/05403/0001/054030001.pdf
Field tests on 8 NTU water
in the DR

68. Field Performance of “BioSand”
Table 2 pH, turbidity and E. coli levels in raw and BSF filter waters
in the field
Parameter raw filtered
Mean pH (n =47) 7.4 8.0
Mean turbidity (NTU) (n=47) 8.1 1.3
Mean log10 E. coli MPN/100mL (n=55) 1.7 0.6
http://www.iwaponline.com/wst/05403/0001/054030001.pdf

69. Potters for Peace Pots
 Colloidal silver-enhanced ceramic water purifier
(CWP)
 After firing the filter is coated with colloidal
silver.
 This combination of fine pore size, and the
bactericidal properties of colloidal silver produce
an effective filter
 Filter units are sold for about $10-15 with the
basic plastic receptacle
 Replacement filter elements cost about $4.00
What is the turbidity range that these filters can handle?
How do you wash the filter? What water do you use?

70. Horizontal Roughing Filters
1m/hr filtration rate (through 5+ m of
media)
Usage of HRFs for large schemes has been
limited due to high capital cost and
operational problems in cleaning the filters.
Equivalent surface loading = 10 m/day

71. Roughing Filters
 Filtration through roughing gravity filters at low filtration
rates (12-48 m/day) produces water with low particulate
concentrations, which allow for further treatment in slow
sand filters without the danger of solids overload.
 In large-scale horizontal-flow filter plants, the large pores
enable particles to be most efficiently transported
downward, although particle transport causes part of the
agglomerated solids to move down towards the filter
bottom. Thus, the pore space at the bottom starts to act as a
sludge storage basin, and the roughing filters need to be
drained periodically. Further development of drainage
methods is needed to improve efficiency in this area.

72. Roughing Filters
 Roughing filters remove particulate of colloidal size
without addition of flocculants, large solids storage
capacity at low head loss, and a simple technology.
 But there are only 11 articles on the topic listed in
 (see articles per year)
 They have not devised a cleaning method that works
Size comparison to floc/sed systems?

73. Multistage Filtration
 The “Other” low tech option for
communities using surface waters
 Uses no coagulants
 Gravel roughing filters
 Polished with slow sand filters
 Large capital costs for construction
 No chemical costs
 Labor intensive operation
What is the tank area of a multistage filtration
plant in comparison with an AguaClara plant?

74. Conclusions…
Many different filtration technologies are
available, especially for POU
Filters are well suited for taking clean water
and making it cleaner. They are not able to
treat very turbid surface waters
Pretreat using flocculation/sedimentation
(AguaClara) or roughing filters (high capital
cost and maintenance problems)

75. Conclusions
Filters could remove particles more
efficiently if the _________ efficiency were
increased
SSF remove particles by two mechanisms
____________
______________________________________
Completely at the mercy of the raw water!
We need to learn what is required to make
ALL of the filter media “sticky” in SSF and
in RSF
Predation
Sticky aluminum polymer that coats the sand
attachment

76. References
 Ken Sutherland, (2008). Filters and Filtration Handbook, 5th Edition
 Tobiason, J. E. and C. R. O'Melia (1988). "Physicochemical Aspects of
Particle Removal in Depth Filtration." Journal American Water Works
Association 80(12): 54-64.
 Yao, K.-M., M. T. Habibian, et al. (1971). "Water and Waste Water Filtration:
Concepts and Applications." Environmental Science and Technology 5(11):
1105.
 M.A. Elliott*, C.E. Stauber, F. Koksal, K.R. Liang, D.K. Huslage, F.A.
DiGiano, M.D. Sobsey. (2006) The operation, flow conditions and microbial
reductions of an intermittently operated, household-scale slow sand filter

77. Any Questions or Additions

78. THANK YOU

79.  Define the following terms:
[Filtration, etc]
Respond to the following questions:
Give a detailed account of ………………
Explain in details the process of …………..
Describe in details with examples the…………
With examples, illustrate the pharmaceutical applications of ……

80. Group work discussional questions:
Explain in details the process of………
Describe with examples in details the…………..
With examples, illustrate the pharmaceutical applications of…….

81. Contact Points