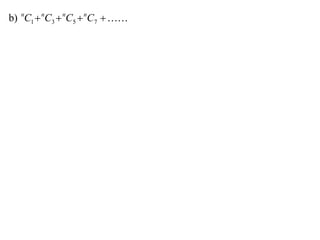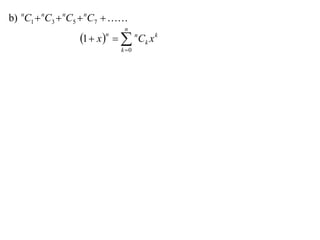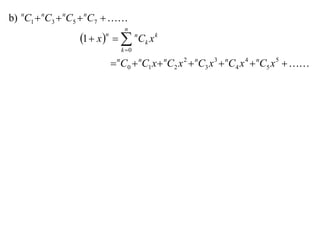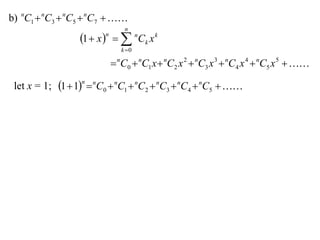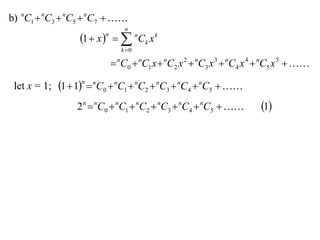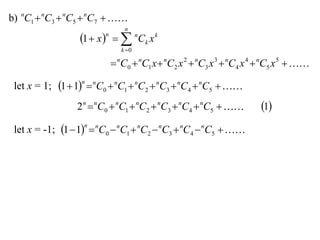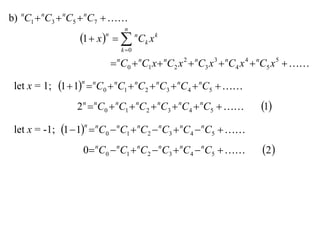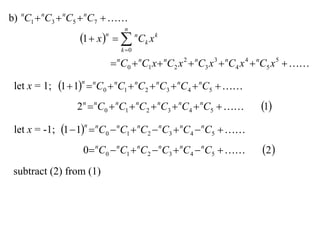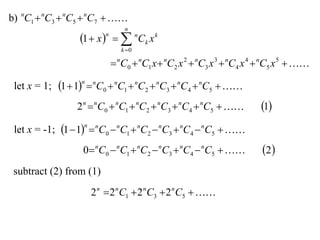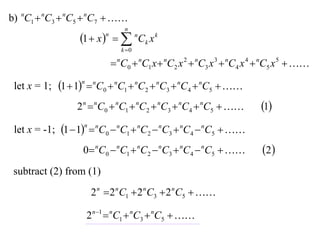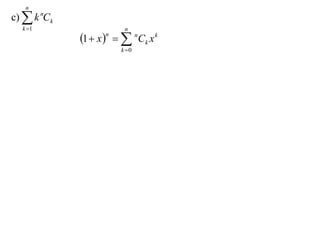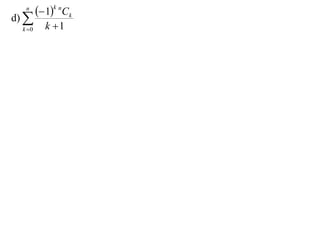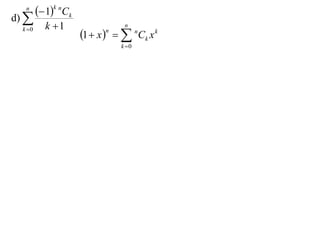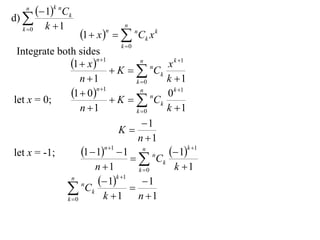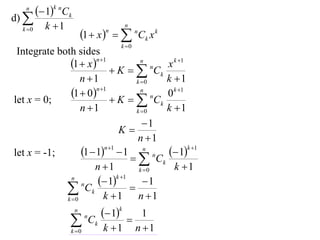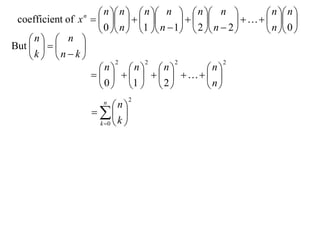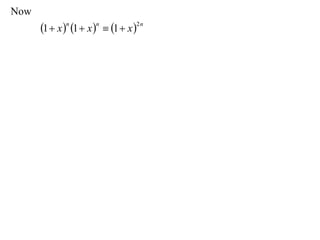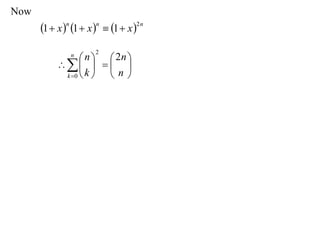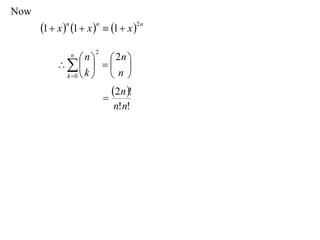The document discusses relationships between binomial coefficients. It introduces the binomial theorem, which expresses (1 + x)n as the sum of terms involving binomial coefficients nCk and powers of x from k = 0 to k = n. It provides two examples: (1) Finding the sum of all binomial coefficients from k = 1 to n, which equals 2n - 1. (2) Finding the sum of binomial coefficients with odd indices, which can be determined by subtracting equations obtained by setting x = 1 and x = -1 in the binomial theorem.

1. Relationships Between
Binomial Coefficients

2. Relationships Between
Binomial Coefficients
Binomial Theorem

3. Relationships Between
Binomial Coefficients
n
Binomial Theorem 1  x n 
 n
Ck x k
k 0

4. Relationships Between
Binomial Coefficients
n
Binomial Theorem 1  x n 
 n
Ck x k
k 0
 nC0  nC1 x  nC2 x 2   nCk x k   nCn x n

5. Relationships Between
Binomial Coefficients
n
Binomial Theorem 1  x n 
 n
Ck x k
k 0
 nC0  nC1 x  nC2 x 2   nCk x k   nCn x n
e.g. (i) Find the values of;
n
a) nCk
k 1

6. Relationships Between
Binomial Coefficients
n
Binomial Theorem 1  x n 
 n
Ck x k
k 0
 nC0  nC1 x  nC2 x 2   nCk x k   nCn x n
e.g. (i) Find the values of;
n n
a) Ck n
1  x    nCk x k
n
k 1 k 0

7. Relationships Between
Binomial Coefficients
n
Binomial Theorem 1  x n 
 n
Ck x k
k 0
 nC0  nC1 x  nC2 x 2   nCk x k   nCn x n
e.g. (i) Find the values of;
n n
a) Ck n
1  x    nCk x k
n
k 1 k 0
n
let x = 1; 1  1n   nCk 1k
k 0

8. Relationships Between
Binomial Coefficients
n
Binomial Theorem 1  x n 
 n
Ck x k
k 0
 nC0  nC1 x  nC2 x 2   nCk x k   nCn x n
e.g. (i) Find the values of;
n n
a) Ck n
1  x    nCk x k
n
k 1 k 0
n
let x = 1; 1  1n   nCk 1k
k 0
n
2 n   nCk
k 0

9. Relationships Between
Binomial Coefficients
n
Binomial Theorem 1  x n 
 n
Ck x k
k 0
 nC0  nC1 x  nC2 x 2   nCk x k   nCn x n
e.g. (i) Find the values of;
n n
a) Ck n
1  x    nCk x k
n
k 1 k 0
n
let x = 1; 1  1n   nCk 1k
k 0
n
2 n   nCk
k 0
n
2 n  n C0   n C k
k 1

10. Relationships Between
Binomial Coefficients
n
Binomial Theorem 1  x n 
 n
Ck x k
k 0
 nC0  nC1 x  nC2 x 2   nCk x k   nCn x n
e.g. (i) Find the values of;
n n
a) Ck
n
n
1  x    Ck x
n n k
 n
C k  2 n  n C0
k 1 k 0 k 1
n
let x = 1; 1  1n   nCk 1k
k 0
n
2 n   nCk
k 0
n
2 n  n C0   n C k
k 1

11. Relationships Between
Binomial Coefficients
n
Binomial Theorem 1  x n 
 n
Ck x k
k 0
 nC0  nC1 x  nC2 x 2   nCk x k   nCn x n
e.g. (i) Find the values of;
n n
a) Ck
n
n
1  x    Ck x
n n k
 n
C k  2 n  n C0
k 1 k 0 k 1
n n
let x = 1; 1  1n   nCk 1k  n
Ck  2 n  1
k 0 k 1
n
2 n   nCk
k 0
n
2 n  n C0   n C k
k 1

12. b) nC1  nC3  nC5  nC7  

13. b) nC1  nC3  nC5  nC7  
n
1  x    nCk x k
n
k 0

14. b) nC1  nC3  nC5  nC7  
n
1  x    nCk x k
n
k 0
 nC0  nC1 x  nC2 x 2  nC3 x 3  nC4 x 4  nC5 x 5  

15. b) nC1  nC3  nC5  nC7  
n
1  x    nCk x k
n
k 0
 nC0  nC1 x  nC2 x 2  nC3 x 3  nC4 x 4  nC5 x 5  
let x = 1; 1  1  nC0  nC1  nC2  nC3  nC4  nC5  
n

16. b) nC1  nC3  nC5  nC7  
n
1  x    nCk x k
n
k 0
 nC0  nC1 x  nC2 x 2  nC3 x 3  nC4 x 4  nC5 x 5  
let x = 1; 1  1  nC0  nC1  nC2  nC3  nC4  nC5  
n
2 n  nC0  nC1  nC2  nC3  nC4  nC5   1

17. b) nC1  nC3  nC5  nC7  
n
1  x    nCk x k
n
k 0
 nC0  nC1 x  nC2 x 2  nC3 x 3  nC4 x 4  nC5 x 5  
let x = 1; 1  1  nC0  nC1  nC2  nC3  nC4  nC5  
n
2 n  nC0  nC1  nC2  nC3  nC4  nC5   1
let x = -1; 1  1  nC0  nC1  nC2  nC3  nC4  nC5  
n

18. b) nC1  nC3  nC5  nC7  
n
1  x    nCk x k
n
k 0
 nC0  nC1 x  nC2 x 2  nC3 x 3  nC4 x 4  nC5 x 5  
let x = 1; 1  1  nC0  nC1  nC2  nC3  nC4  nC5  
n
2 n  nC0  nC1  nC2  nC3  nC4  nC5   1
let x = -1; 1  1  nC0  nC1  nC2  nC3  nC4  nC5  
n
0 nC0  nC1  nC2  nC3  nC4  nC5   2 

19. b) nC1  nC3  nC5  nC7  
n
1  x    nCk x k
n
k 0
 nC0  nC1 x  nC2 x 2  nC3 x 3  nC4 x 4  nC5 x 5  
let x = 1; 1  1  nC0  nC1  nC2  nC3  nC4  nC5  
n
2 n  nC0  nC1  nC2  nC3  nC4  nC5   1
let x = -1; 1  1  nC0  nC1  nC2  nC3  nC4  nC5  
n
0 nC0  nC1  nC2  nC3  nC4  nC5   2 
subtract (2) from (1)

20. b) nC1  nC3  nC5  nC7  
n
1  x    nCk x k
n
k 0
 nC0  nC1 x  nC2 x 2  nC3 x 3  nC4 x 4  nC5 x 5  
let x = 1; 1  1  nC0  nC1  nC2  nC3  nC4  nC5  
n
2 n  nC0  nC1  nC2  nC3  nC4  nC5   1
let x = -1; 1  1  nC0  nC1  nC2  nC3  nC4  nC5  
n
0 nC0  nC1  nC2  nC3  nC4  nC5   2 
subtract (2) from (1)
2 n  2 n C1  2 n C3  2 n C5  

21. b) nC1  nC3  nC5  nC7  
n
1  x    nCk x k
n
k 0
 nC0  nC1 x  nC2 x 2  nC3 x 3  nC4 x 4  nC5 x 5  
let x = 1; 1  1  nC0  nC1  nC2  nC3  nC4  nC5  
n
2 n  nC0  nC1  nC2  nC3  nC4  nC5   1
let x = -1; 1  1  nC0  nC1  nC2  nC3  nC4  nC5  
n
0 nC0  nC1  nC2  nC3  nC4  nC5   2 
subtract (2) from (1)
2 n  2 n C1  2 n C3  2 n C5  
2 n 1  nC1  nC3  nC5  

22. n
c)  k nCk
k 1

23. n
c)  k nCk
k 1 n
1  x    nCk x k
n
k 0

24. n
c)  k nCk
k 1 n
1  x    nCk x k
n
k 0
Differentiate both sides

25. n
c)  k nCk
k 1 n
1  x    nCk x k
n
k 0
Differentiate both sides
n
n1  x    k nCk x k 1
n 1
k 0

26. n
c)  k nCk
k 1 n
1  x    nCk x k
n
k 0
Differentiate both sides
n
n1  x    k nCk x k 1
n 1
k 0
n
n1  1   k nCk
n 1
let x = 1;
k 0

27. n
c)  k nCk
k 1 n
1  x    nCk x k
n
k 0
Differentiate both sides
n
n1  x    k nCk x k 1
n 1
k 0
n
n1  1   k nCk
n 1
let x = 1;
k 0
n
n 2  0  C0   k nCk
n 1 n
k 1

28. n
c)  k nCk
k 1 n
1  x    nCk x k
n
k 0
Differentiate both sides
n
n1  x    k nCk x k 1
n 1
k 0
n
n1  1   k nCk
n 1
let x = 1;
k 0
n
n 2  0  C0   k nCk
n 1 n
k 1
n
k C  n 2 
n n 1
k
k 1

29. n
 1k nCk
d) 
k 0 k 1

30. n
 1k nCk
d) 
k 1 n
1  x    nCk x k
k 0 n
k 0

31. n
 1k nCk
d) 
k 1 n
1  x    nCk x k
k 0 n
k 0
Integrate both sides

32. n
 1k nCk
d) 
k 1 n
1  x    nCk x k
k 0 n
k 0
Integrate both sides
1  x n1 n
x k 1
 K   Ck n
n 1 k 0 k 1

33. n
 1k nCk
d) 
k 1 n
1  x    nCk x k
k 0 n
k 0
Integrate both sides
1  x n1 n
x k 1
 K   nCk
n 1 k 0 k 1
1  0n 1 n
0 k 1
let x = 0;  K   nCk
n 1 k 0 k 1

34. n
 1k nCk
d) 
k 1 n
1  x    nCk x k
k 0 n
k 0
Integrate both sides
1  x n1 n
x k 1
 K   nCk
n 1 k 0 k 1
1  0n 1 n
0 k 1
let x = 0;  K   nCk
n 1 k 0 k 1
1
K
n 1

35. n
 1k nCk
d) 
k 1 n
1  x    nCk x k
k 0 n
k 0
Integrate both sides
1  x n1  K  n nC x k 1
n 1
 k k 1
k 0
1  0n 1  K  n nC 0 k 1
let x = 0;
n 1
 k k 1
k 0
1
K
n 1
1  1n 1  1  n nC  1k 1
 k k 1
let x = -1;
n 1 k 0

36. n
 1k nCk
d) 
k 1 n
1  x    nCk x k
k 0 n
k 0
Integrate both sides
1  x n1  K  n nC x k 1
n 1
 k k 1
k 0
1  0n 1  K  n nC 0 k 1
let x = 0;
n 1
 k k 1
k 0
1
K
n 1
1  1n 1  1  n nC  1k 1
 k k 1
let x = -1;
n 1 k 0
n
 1k 1   1
 Ck k  1 n  1
k 0
n

37. n
 1k nCk
d) 
k 1 n
1  x    nCk x k
k 0 n
k 0
Integrate both sides
1  x n1  K  n nC x k 1
n 1
 k k 1
k 0
1  0n 1  K  n nC 0 k 1
let x = 0;
n 1
 k k 1
k 0
1
K
n 1
1  1n 1  1  n nC  1k 1
 k k 1
let x = -1;
n 1 k 0
n
 1k 1   1
 Ck k  1 n  1
k 0
n
n
 1k  1
 Ck
n
k 0 k 1 n 1

38. ii  By equating the coefficients of x n on both sides of the identity;
1  x  1  x   1  x 
n n 2n
show that;
 n  2n !
n 2
  k   n!2
k 0 


39. ii  By equating the coefficients of x n on both sides of the identity;
1  x n 1  x n  1  x 2 n
show that;
 n  2n !
n 2
  k   n!2

n k 0 
1  x n   nCk x k
k 0

40. ii  By equating the coefficients of x n on both sides of the identity;
1  x n 1  x n  1  x 2 n
show that;
 n  2n !
n 2
  k   n!2

n k 0 
1  x n   nCk x k
k 0
 C  nC1 x  nC2 x 2   nCn  2 x n  2  nCn 1 x n 1  nCn x n
n
0

41. ii  By equating the coefficients of x n on both sides of the identity;
1  x n 1  x n  1  x 2 n
show that;
 n  2n !
n 2
  k   n!2

n k 0 
1  x n   nCk x k
k 0
 C  nC1 x  nC2 x 2   nCn  2 x n  2  nCn 1 x n 1  nCn x n
n
0
coefficient of x n in 1  x  1  x 
n n

42. ii  By equating the coefficients of x n on both sides of the identity;
1  x n 1  x n  1  x 2 n
show that;
 n  2n !
n 2
  k   n!2

n k 0 
1  x n   nCk x k
k 0
 C  nC1 x  nC2 x 2   nCn  2 x n  2  nCn 1 x n 1  nCn x n
n
0
coefficient of x n in 1  x  1  x 
n n
 nC0  nC1 x nC2 x 2   nCn2 x n2  nCn1 x n1  nCn x n 
  nC0  nC1 x  nC2 x 2   nCn2 x n2  nCn1 x n1  nCn x n 

43. ii  By equating the coefficients of x n on both sides of the identity;
1  x n 1  x n  1  x 2 n
show that;
 n  2n !
n 2
  k   n!2

n k 0 
1  x n   nCk x k
k 0
 C  nC1 x  nC2 x 2   nCn  2 x n  2  nCn 1 x n 1  nCn x n
n
0
coefficient of x n in 1  x  1  x 
n n
 nC0  nC1 x nC2 x 2   nCn2 x n2  nCn1 x n1  nCn x n 
  nC0  nC1 x  nC2 x 2   nCn2 x n2  nCn1 x n1  nCn x n 
 n  n  n
    x
 0  n 
 n  n2  n  2  n  n1  n   n  n  n 
  x  x   x  x   x  
 n  2 2  n  1 1   n   0 

44. ii  By equating the coefficients of x n on both sides of the identity;
1  x n 1  x n  1  x 2 n
show that;
 n  2n !
n 2
  k   n!2

n k 0 
1  x n   nCk x k
k 0
 C  nC1 x  nC2 x 2   nCn  2 x n  2  nCn 1 x n 1  nCn x n
n
0
coefficient of x n in 1  x  1  x 
n n
 nC0  nC1 x nC2 x 2   nCn2 x n2  nCn1 x n1  nCn x n 
  nC0  nC1 x  nC2 x 2   nCn2 x n2  nCn1 x n1  nCn x n 
 n  n  n  n   n  n1
    x    x x
 0  n  1   n  1

45. ii  By equating the coefficients of x n on both sides of the identity;
1  x n 1  x n  1  x 2 n
show that;
 n  2n !
n 2
  k   n!2

n k 0 
1  x n   nCk x k
k 0
 C  nC1 x  nC2 x 2   nCn  2 x n  2  nCn 1 x n 1  nCn x n
n
0
coefficient of x n in 1  x  1  x 
n n
 nC0  nC1 x nC2 x 2   nCn2 x n2  nCn1 x n1  nCn x n 
  nC0  nC1 x  nC2 x 2   nCn2 x n2  nCn1 x n1  nCn x n 
 n  n  n  n   n  n1  n  2  n  n2
    x    x x   x  x
 0  n  1   n  1  2  n  2

46. ii  By equating the coefficients of x n on both sides of the identity;
1  x n 1  x n  1  x 2 n
show that;
 n  2n !
n 2
  k   n!2

n k 0 
1  x n   nCk x k
k 0
 C  nC1 x  nC2 x 2   nCn  2 x n  2  nCn 1 x n 1  nCn x n
n
0
coefficient of x n in 1  x  1  x 
n n
 nC0  nC1 x nC2 x 2   nCn2 x n2  nCn1 x n1  nCn x n 
  nC0  nC1 x  nC2 x 2   nCn2 x n2  nCn1 x n1  nCn x n 
 n  n  n  n   n  n1  n  2  n  n2
    x    x x   x  x
 0  n  1   n  1  2  n  2
 n  n2  n  2  n  n1  n   n  n  n 
  x  x   x  x   x  
 n  2 2  n  1 1   n   0 

47.  n  n   n  n   n  n   n  n 
coefficient of x       
n
          
 0  n  1  n  1  2  n  2   n  0 

48.  n  n   n  n   n  n   n  n 
coefficient of x       
n
          
 0  n  1  n  1  2  n  2   n  0 
n  n 
But     
k  n  k 

49.  n  n   n  n   n  n   n  n 
coefficient of x       
n
          
 0  n  1  n  1  2  n  2   n  0 
n  n 
But     
k  n  k  2 2 2 2
 n n n  n
           
 0  1   2  n

50.  n  n   n  n   n  n   n  n 
coefficient of x       
n
          
 0  n  1  n  1  2  n  2   n  0 
n  n 
But     
k  n  k  2 2 2 2
 n n n  n
           
 0  1   2  n
2
n
n
  
k 0  k 

51.  n  n   n  n   n  n   n  n 
coefficient of x       
n
          
 0  n  1  n  1  2  n  2   n  0 
n  n 
But     
k  n  k  2 2 2 2
 n n n  n
           
 0  1   2  n
2
n
n
  
k 0  k 
coefficient of x n in 1  x 
2n

52.  n  n   n  n   n  n   n  n 
coefficient of x       
n
          
 0  n  1  n  1  2  n  2   n  0 
n  n 
But     
k  n  k  2 2 2 2
 n n n  n
           
 0  1   2  n
2
n
n
  
k 0  k 
coefficient of x n in 1  x 
2n
 2n   2n   2n  2  2n  n  2n  2 n
1  x 
2n
     x   x     x     x
0   1   2  n  2n 

53.  n  n   n  n   n  n   n  n 
coefficient of x       
n
          
 0  n  1  n  1  2  n  2   n  0 
n  n 
But     
k  n  k  2 2 2 2
 n n n  n
           
 0  1   2  n
2
n
n
  
k 0  k 
coefficient of x n in 1  x 
2n
 2n   2n   2n  2  2n  n  2n  2 n
1  x 
2n
     x   x     x     x
0   1   2  n  2n 

54.  n  n   n  n   n  n   n  n 
coefficient of x       
n
          
 0  n  1  n  1  2  n  2   n  0 
n  n 
But     
k  n  k  2 2 2 2
 n n n  n
           
 0  1   2  n
2
n
n
  
k 0  k 
coefficient of x n in 1  x 
2n
 2n   2n   2n  2  2n  n  2n  2 n
1  x 
2n
     x   x     x     x
0   1   2  n  2n 
 2n 
coefficient of x   
n
n

55. Now
1  x n 1  x n  1  x 2 n

56. Now
1  x n 1  x n  1  x 2 n
2
n
 n   2n 
     
k 0  k  n

57. Now
1  x n 1  x n  1  x 2 n
2
n
 n   2n 
     
k 0  k  n
2n !

n!n!

58. Now
1  x n 1  x n  1  x 2 n
2
n
 n   2n 
     
k 0  k  n
2n !

n!n!
2n !

n!2

59. Now
1  x n 1  x n  1  x 2 n
2
n
 n   2n 
     
k 0  k  n

2n ! Exercise 5F;
n!n! 4, 5, 6, 8, 10,15
2n !

n!2 + worksheets