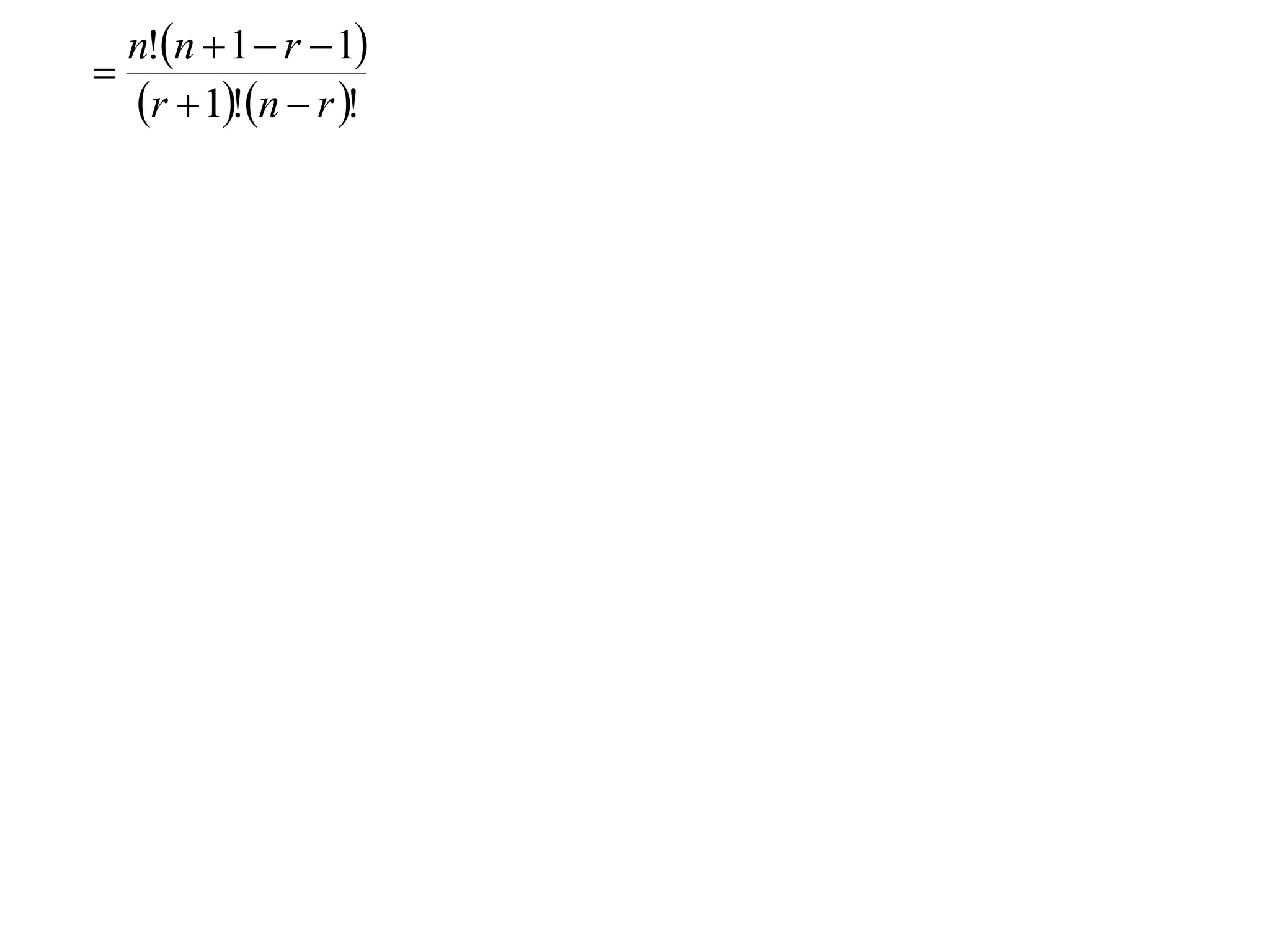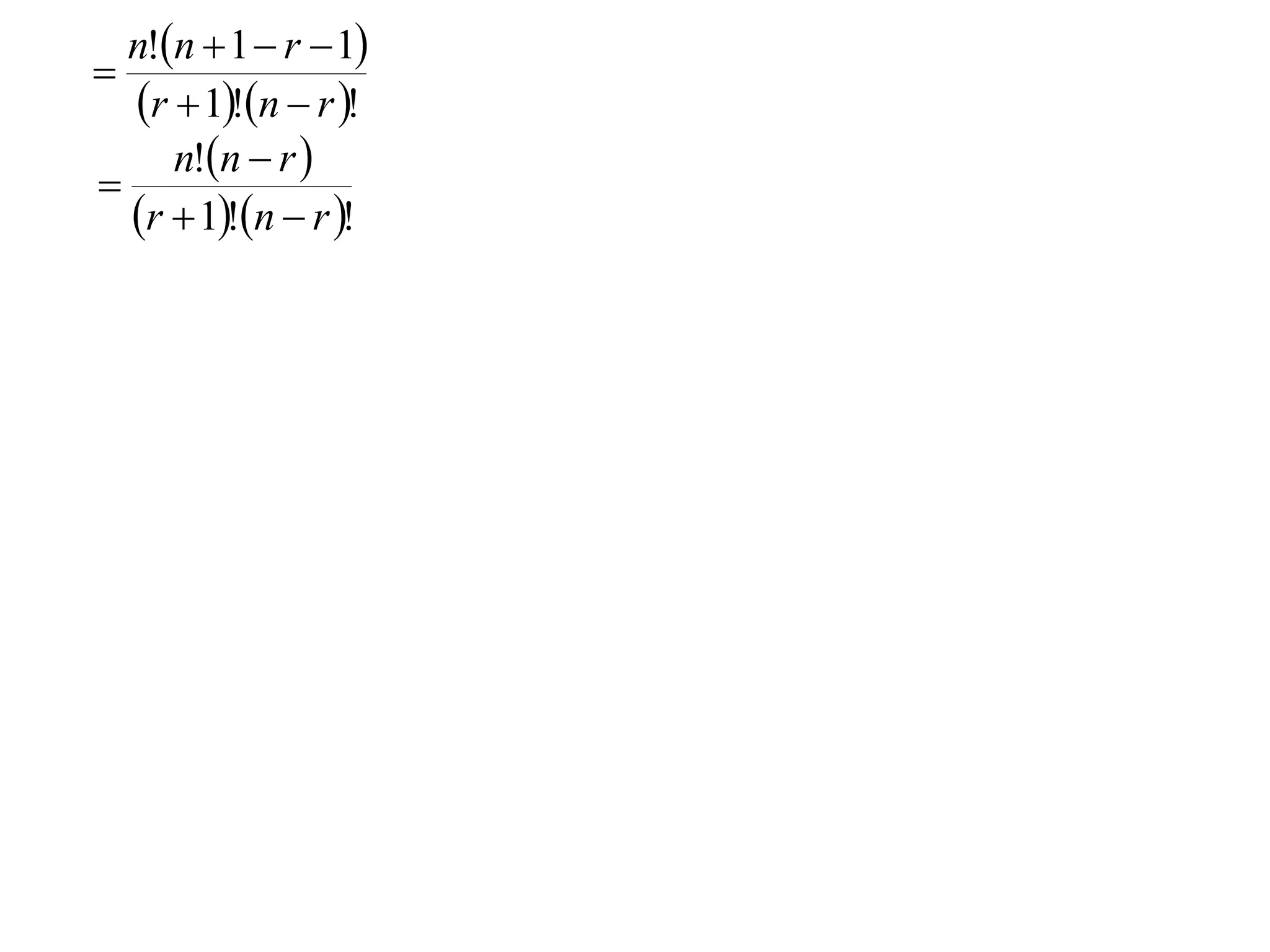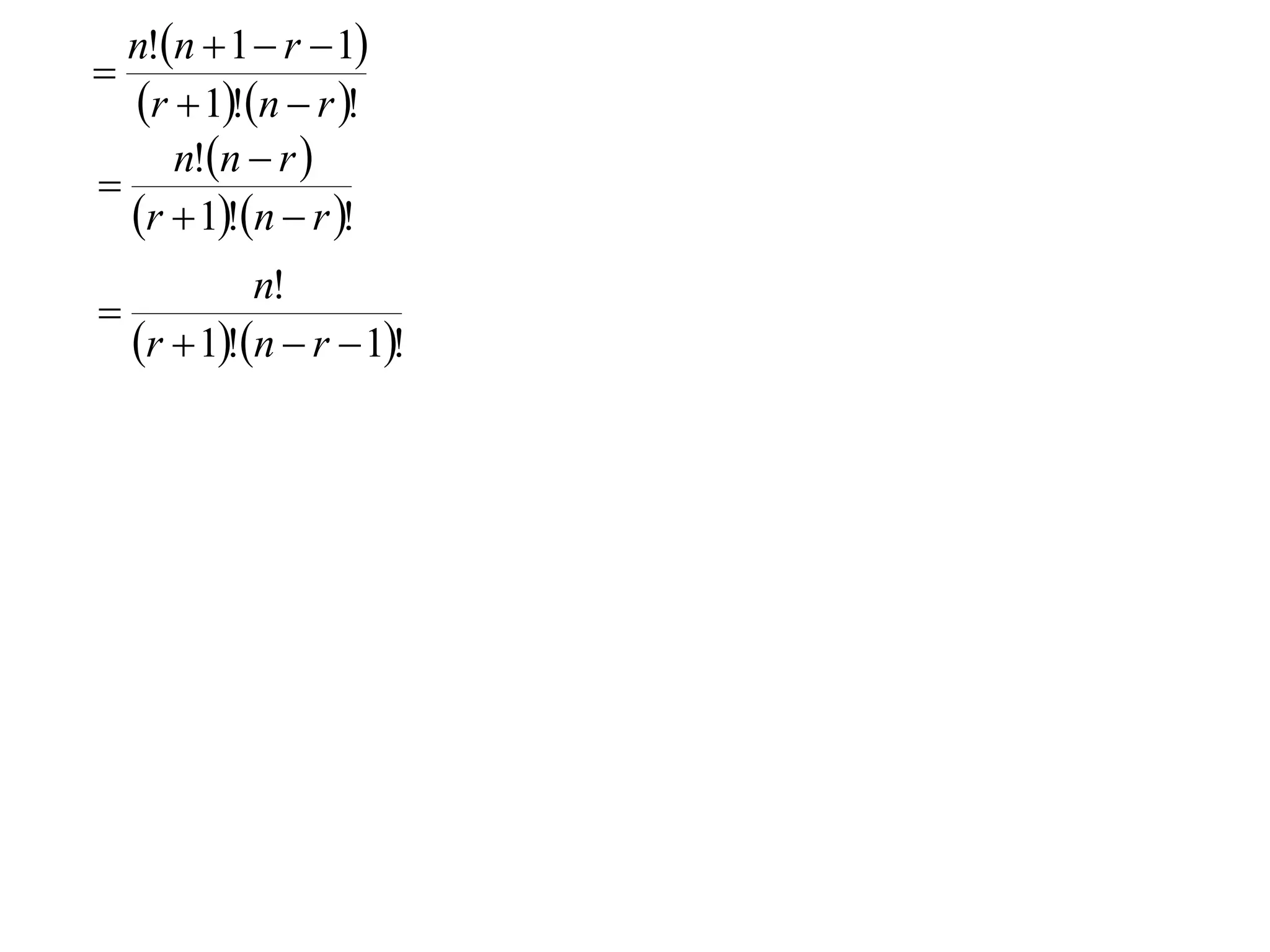The document proves a formula for calculating binomial coefficients without using Pascal's triangle. It does so through a multi-step proof by induction. First, it shows the formula holds for k=0. Then it assumes the formula holds for some integer k=r, and shows it also holds for k=r+1. Therefore, by induction the formula holds for all positive integer values of k. The document also explains how this relates to the binomial theorem for expanding binomial expressions.

1. Calculating Coefficients
without Pascal’s Triangle

2. Calculating Coefficients
without Pascal’s Triangle
n!
n
Ck 
k!n  k !

3. Calculating Coefficients
without Pascal’s Triangle
n!
n
Ck 
k!n  k !
Proof

4. Calculating Coefficients
without Pascal’s Triangle
n!
n
Ck 
k!n  k !
Proof
Step 1: Prove true for k = 0

5. Calculating Coefficients
without Pascal’s Triangle
n!
n
Ck 
k!n  k !
Proof
Step 1: Prove true for k = 0
LHS  nC0
1

6. Calculating Coefficients
without Pascal’s Triangle
n!
n
Ck 
k!n  k !
Proof
Step 1: Prove true for k = 0
n!
LHS  nC0 RHS 
0!n!
1
n!

n!
1

7. Calculating Coefficients
without Pascal’s Triangle
n!
n
Ck 
k!n  k !
Proof
Step 1: Prove true for k = 0
n!
LHS  nC0 RHS 
0!n!
1
n!

n!
 LHS  RHS 1

8. Calculating Coefficients
without Pascal’s Triangle
n!
n
Ck 
k!n  k !
Proof
Step 1: Prove true for k = 0
n!
LHS  nC0 RHS 
0!n!
1
n!

n!
 LHS  RHS 1
Hence the result is true for k = 0

9. Step 2 : Assume the result is true for k  r where r is an integer  0

10. Step 2 : Assume the result is true for k  r where r is an integer  0
n!
i.e.n Cr 
r!n  r !

11. Step 2 : Assume the result is true for k  r where r is an integer  0
n!
i.e.n Cr 
r!n  r !
Step 3 : Prove the result is true for k  r  1

12. Step 2 : Assume the result is true for k  r where r is an integer  0
n!
i.e.n Cr 
r!n  r !
Step 3 : Prove the result is true for k  r  1
n!
i.e.n Cr 1 
r  1!n  r  1!

13. Step 2 : Assume the result is true for k  r where r is an integer  0
n!
i.e.n Cr 
r!n  r !
Step 3 : Prove the result is true for k  r  1
n!
i.e.n Cr 1 
r  1!n  r  1!
Proof

14. Step 2 : Assume the result is true for k  r where r is an integer  0
n!
i.e.n Cr 
r!n  r !
Step 3 : Prove the result is true for k  r  1
n!
i.e.n Cr 1 
r  1!n  r  1!
Proof
n 1
Cr 1  nCr  nCr 1

15. Step 2 : Assume the result is true for k  r where r is an integer  0
n!
i.e.n Cr 
r!n  r !
Step 3 : Prove the result is true for k  r  1
n!
i.e.n Cr 1 
r  1!n  r  1!
Proof
n 1
Cr 1  nCr  nCr 1
n
Cr 1  n1Cr 1  nCr

16. Step 2 : Assume the result is true for k  r where r is an integer  0
n!
i.e.n Cr 
r!n  r !
Step 3 : Prove the result is true for k  r  1
n!
i.e.n Cr 1 
r  1!n  r  1!
Proof
n 1
Cr 1  nCr  nCr 1
n
Cr 1  n1Cr 1  nCr
n  1! n!
 
r  1!n  r ! r!n  r!

17. Step 2 : Assume the result is true for k  r where r is an integer  0
n!
i.e.n Cr 
r!n  r !
Step 3 : Prove the result is true for k  r  1
n!
i.e.n Cr 1 
r  1!n  r  1!
Proof
n 1
Cr 1  nCr  nCr 1
n
Cr 1  n1Cr 1  nCr
n  1! n!
 
r  1!n  r ! r!n  r!
n  1!n!r  1

r  1!n  r !

18. Step 2 : Assume the result is true for k  r where r is an integer  0
n!
i.e.n Cr 
r!n  r !
Step 3 : Prove the result is true for k  r  1
n!
i.e.n Cr 1 
r  1!n  r  1!
Proof
n 1
Cr 1  nCr  nCr 1
n
Cr 1  n1Cr 1  nCr
n  1! n!
 
r  1!n  r ! r!n  r!
n  1!n!r  1

r  1!n  r !
n!n  1  r  1

r  1!n  r !

19. n!n  1  r  1

r  1!n  r !

20. n!n  1  r  1

r  1!n  r !
n!n  r 

r  1!n  r !

21. n!n  1  r  1

r  1!n  r !
n!n  r 

r  1!n  r !
n!

r  1!n  r  1!

22. n!n  1  r  1

r  1!n  r !
n!n  r 

r  1!n  r !
n!

r  1!n  r  1!
Hence the result is true for k = r + 1 if it is also true for k = r

23. n!n  1  r  1

r  1!n  r !
n!n  r 

r  1!n  r !
n!

r  1!n  r  1!
Hence the result is true for k = r + 1 if it is also true for k = r
Step 4: Hence the result is true for all positive integral values of n
by induction

24. The Binomial Theorem

25. The Binomial Theorem
1  x n  nC0  nC1 x  nC2 x 2   nCk x k   nCn x n

26. The Binomial Theorem
1  x n  nC0  nC1 x  nC2 x 2   nCk x k   nCn x n
n
  nCk x k
k 0

27. The Binomial Theorem
1  x n  nC0  nC1 x  nC2 x 2   nCk x k   nCn x n
n
  nCk x k
k 0
n!
where Ck 
n
and n is a positive integer
k!n  k !

28. The Binomial Theorem
1  x n  nC0  nC1 x  nC2 x 2   nCk x k   nCn x n
n
  nCk x k
k 0
n!
where Ck 
n
and n is a positive integer
k!n  k !
NOTE: there are (n + 1) terms

29. The Binomial Theorem
1  x n  nC0  nC1 x  nC2 x 2   nCk x k   nCn x n
n
  nCk x k
k 0
n!
where Ck  n
and n is a positive integer
k!n  k !
NOTE: there are (n + 1) terms
This extends to; n
a  b    n C k a n  k b k
n
k 0

30. The Binomial Theorem
1  x n  nC0  nC1 x  nC2 x 2   nCk x k   nCn x n
n
  nCk x k
k 0
n!
where Ck  n
and n is a positive integer
k!n  k !
NOTE: there are (n + 1) terms
This extends to; n
a  b    n C k a n  k b k
n
k 0
e.g . Evaluate 11C4

31. The Binomial Theorem
1  x n  nC0  nC1 x  nC2 x 2   nCk x k   nCn x n
n
  nCk x k
k 0
n!
where Ck  n
and n is a positive integer
k!n  k !
NOTE: there are (n + 1) terms
This extends to; n
a  b    n C k a n  k b k
n
k 0
11!
e.g . Evaluate 11C4 11
C4 
4!7!

32. The Binomial Theorem
1  x n  nC0  nC1 x  nC2 x 2   nCk x k   nCn x n
n
  nCk x k
k 0
n!
where Ck  n
and n is a positive integer
k!n  k !
NOTE: there are (n + 1) terms
This extends to; n
a  b    n C k a n  k b k
n
k 0
11!
e.g . Evaluate 11C4 11
C4 
4!7!
1110  9  8

4  3  2 1

33. The Binomial Theorem
1  x n  nC0  nC1 x  nC2 x 2   nCk x k   nCn x n
n
  nCk x k
k 0
n!
where Ck  n
and n is a positive integer
k!n  k !
NOTE: there are (n + 1) terms
This extends to; n
a  b    n C k a n  k b k
n
k 0
11!
e.g . Evaluate 11C4 11
C4 
4!7!
1110  9  8

4  3  2 1

34. The Binomial Theorem
1  x n  nC0  nC1 x  nC2 x 2   nCk x k   nCn x n
n
  nCk x k
k 0
n!
where Ck  n
and n is a positive integer
k!n  k !
NOTE: there are (n + 1) terms
This extends to; n
a  b    n C k a n  k b k
n
k 0
11!
e.g . Evaluate 11C4 11
C4 
4!7! 3
1110  9  8

4  3  2 1

35. The Binomial Theorem
1  x n  nC0  nC1 x  nC2 x 2   nCk x k   nCn x n
n
  nCk x k
k 0
n!
where Ck  n
and n is a positive integer
k!n  k !
NOTE: there are (n + 1) terms
This extends to; n
a  b    n C k a n  k b k
n
k 0
11!
e.g . Evaluate 11C4 11
C4 
4!7! 3
1110  9  8

4  3  2 1
 330

36. (ii) Find the value of n so that;

37. (ii) Find the value of n so that;
a) nC5  nC8

38. (ii) Find the value of n so that;
a) nC5  nC8
n
Ck  nCnk

39. (ii) Find the value of n so that;
a) nC5  nC8
n
Ck  nCnk
8  n  5
n  13

40. (ii) Find the value of n so that;
a) nC5  nC8 b) nC7  nC8  20C8
n
Ck  nCnk
8  n  5
n  13

41. (ii) Find the value of n so that;
a) nC5  nC8 b) nC7  nC8  20C8
n 1
n
Ck  Cnk
n
Ck  n1Ck 1  nCk
8  n  5
n  13

42. (ii) Find the value of n so that;
a) nC5  nC8 b) nC7  nC8  20C8
n 1
n
Ck  Cnk
n
Ck  n1Ck 1  nCk
8  n  5 n  19
n  13

43. (ii) Find the value of n so that;
a) nC5  nC8 b) nC7  nC8  20C8
n 1
n
Ck  Cnk
n
Ck  n1Ck 1  nCk
8  n  5 n  19
n  13
11
iii  Find the 5th term in the expansion of  5a  3 
 
 b

44. (ii) Find the value of n so that;
a) nC5  nC8 b) nC7  nC8  20C8
n 1
n
Ck  Cnk
n
Ck  n1Ck 1  nCk
8  n  5 n  19
n  13
11
iii  Find the 5th term in the expansion of  5a  3 
 
 b
k
11 k  3 
Tk 1  Ck 5a    
11
 b

45. (ii) Find the value of n so that;
a) nC5  nC8 b) nC7  nC8  20C8
n 1
n
Ck  Cnk
n
Ck  n1Ck 1  nCk
8  n  5 n  19
n  13
11
iii  Find the 5th term in the expansion of  5a  3 
 
 b
k
11 k  3 
Tk 1  Ck 5a    
11
 b
4
7 3
T5  C4 5a    
11
 b

46. (ii) Find the value of n so that;
a) nC5  nC8 b) nC7  nC8  20C8
n 1
n
Ck  Cnk
n
Ck  n1Ck 1  nCk
8  n  5 n  19
n  13
11
iii  Find the 5th term in the expansion of  5a  3 
 
 b
k
11 k  3 
Tk 1  Ck 5a    
11
 b
4
7 3
T5  C4 5a    
11
 b
11
C 4 5 7 34 a 7

b4

47. (ii) Find the value of n so that;
a) nC5  nC8 b) nC7  nC8  20C8
n 1
n
Ck  Cnk
n
Ck  n1Ck 1  nCk
8  n  5 n  19
n  13
11
iii  Find the 5th term in the expansion of  5a  3 
 
 b
k
11 k  3 
Tk 1  Ck 5a    
11
 b
4
7 3
T5  C4 5a    
11
 b
11
C 4 5 7 34 a 7
 unsimplified
b4

48. (ii) Find the value of n so that;
a) nC5  nC8 b) nC7  nC8  20C8
n 1
n
Ck  Cnk
n
Ck  n1Ck 1  nCk
8  n  5 n  19
n  13
11
iii  Find the 5th term in the expansion of  5a  3 
 
 b
k
11 k  3 
Tk 1  Ck 5a    
11
 b
4
7 3
T5  C4 5a    
11

330  78125  81a 7
 b b4
11
C 4 5 7 34 a 7
 unsimplified
b4

49. (ii) Find the value of n so that;
a) nC5  nC8 b) nC7  nC8  20C8
n 1
n
Ck  Cnk
n
Ck  n1Ck 1  nCk
8  n  5 n  19
n  13
11
iii  Find the 5th term in the expansion of  5a  3 
 
 b
k
11 k  3 
Tk 1  Ck 5a    
11
 b
4
7 3
T5  C4 5a    
11

330  78125  81a 7
 b b4
11
C 4 5 7 34 a 7 2088281250a 7
 unsimplified 
b4 b4

50. 9
iv  Obtain the term independent of x in  3x 2  1 
 
 2x 

51. 9
iv  Obtain the term independent of x in  3x 2  1 
 
k
 2x 
Tk 1  Ck 3 x 
2 9 k  1 
 
9
 2x 

52. 9
iv  Obtain the term independent of x in  3x 2  1 
 
k
 2x 
Tk 1  Ck 3 x 
 1 
2 9 k
 
9
 2x 
term independent of x means term with x 0

53. 9
iv  Obtain the term independent of x in  3x 2  1 
 
k
 2x 
Tk 1  Ck 3 x 
 1 
2 9 k
 
9
 2x 
term independent of x means term with x 0
x  x 
2 9 k 1 k
 x0

54. 9
iv  Obtain the term independent of x in  3x 2  1 
 
k
 2x 
Tk 1  Ck 3 x 
 1 
2 9 k
 
9
 2x 
term independent of x means term with x 0
x  x 
2 9 k 1 k
 x0
x182 k  x k  x 0
18  3k  0
k 6

55. 9
iv  Obtain the term independent of x in  3x 2  1 
 
k
 2x 
Tk 1  Ck 3 x 
 1 2 9 k
 
9
 2x 
term independent of x means term with x 0
x  x 
2 9 k 1 k
 x0
x182 k  x k  x 0
18  3k  0
6 k 6
T7  C6 3 x
9

2 3  1 
 
 2x 

56. 9
iv  Obtain the term independent of x in  3x 2  1 
 
k
 2x 
Tk 1  Ck 3 x 
 1 2 9 k
 
9
 2x 
term independent of x means term with x 0
x  x 
2 9 k 1 k
 x0
x182 k  x k  x 0
18  3k  0
6 k 6
T7  C6 3 x
9

2 3  1 
 
 2x 
9
C6 33
 6
2

57. 9
iv  Obtain the term independent of x in  3x 2  1 
 
k
 2x 
Tk 1  Ck 3 x 
 1 2 9 k
 
9
 2x 
term independent of x means term with x 0
x  x 
2 9 k 1 k
 x0
x182 k  x k  x 0
18  3k  0
6 k 6
T7  C6 3 x
9

2 3  1 
 
 2x 
9
C6 33
 6
2 Exercise 5D; 2, 3, 5, 7, 9, 10ac, 12ac, 13,
14, 15ac, 19, 25