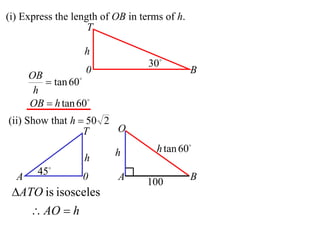
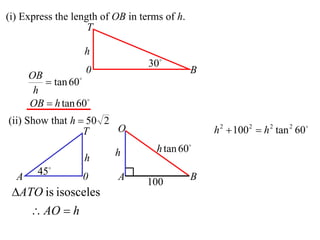
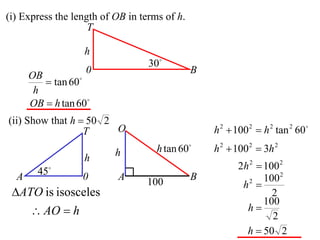
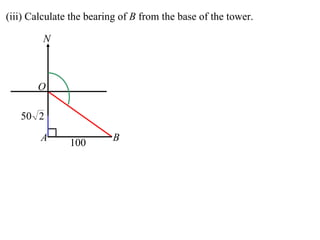
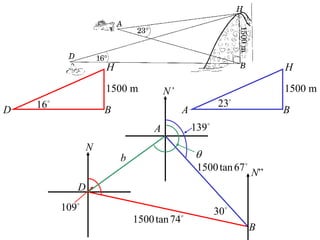
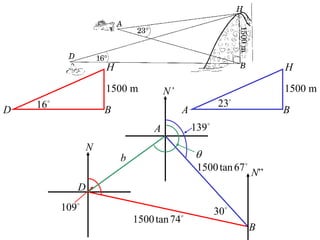
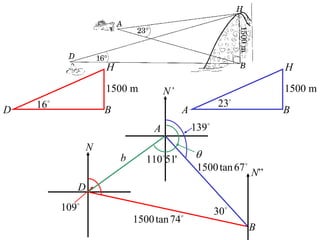
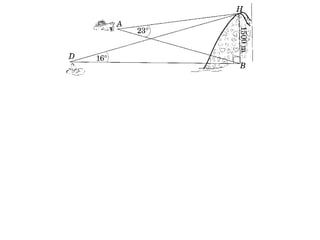
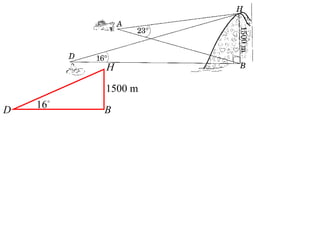
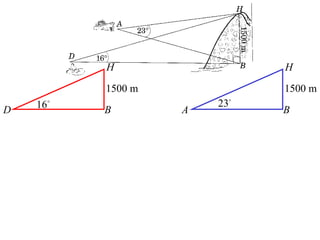
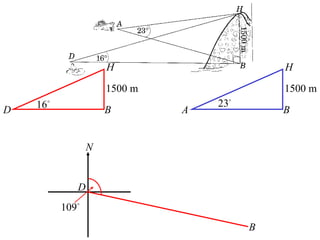
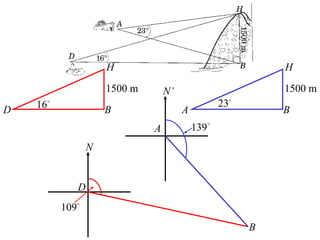
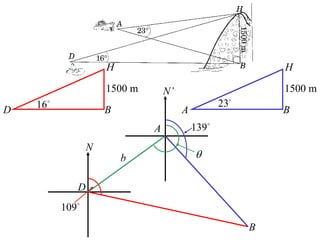
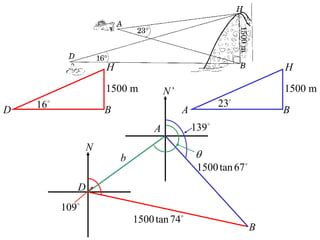
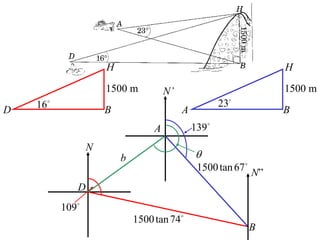
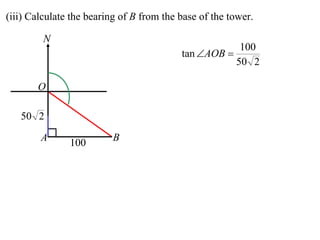
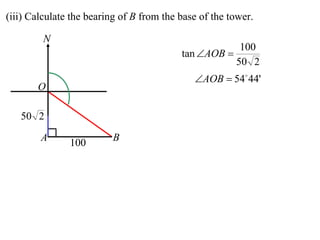
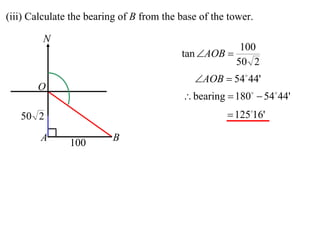
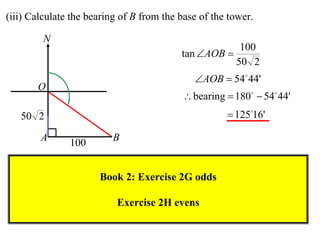
The document discusses trigonometry concepts related to 3D shapes and solving problems involving angles of elevation. Specifically: - When doing 3D trigonometry, it is often useful to redraw shapes in 2D to analyze them. - A worked example problem is shown to find the distance and bearing between a life raft (David's position) and a search vessel (Anna's position) based on angles of elevation they each observe of a mountain peak. - Applying trigonometric relationships involving angles and the mountain's known height, the distance between David and Anna is calculated to be 2799 meters, and the bearing of David from Anna is determined to be 249°51'.

1. 3D Trigonometry

2. 3D Trigonometry
When doing 3D trigonometry it is often useful to redraw all of the
faces of the shape in 2D.

3. 3D Trigonometry
When doing 3D trigonometry it is often useful to redraw all of the
faces of the shape in 2D.
2003 Extension 1 HSC Q7a)
David is in a life raft and Anna is in a cabin cruiser searching for him.
They are in contact by mobile phone. David tells Ana that he can see
Mt Hope. From David’s position the mountain has a bearing of 109 ,
and the angle of elevation to the top of the mountain is 16.
Anna can also see Mt Hope. From her position it has a bearing of 139,
and and the top of the mountain has an angle of elevation of 23 .
The top of Mt Hope is 1500 m above sea level.
Find the distance and bearing of the life raft from Anna’s position.

5. H
1500 m
D 16 B

6. H H
1500 m 1500 m
16 23
D B A B

7. H H
1500 m 1500 m
16 23
D B A B
N
D
109
B

8. H H
1500 m N’ 1500 m
16 23
D B A B
A 139
N
D
109
B

9. H H
1500 m N’ 1500 m
16 23
D B A B
A 139
N
b 
D
109
B

10. BD
 tan 74
1500

11. BD
 tan 74
1500
BD  1500 tan 74

12. BD
 tan 74
1500 Similarly;
BD  1500 tan 74 AB  1500 tan 67 

13. H H
1500 m N’ 1500 m
16 23
D B A B
A 139
N
b 
1500 tan 67 
D
109
1500 tan 74
B

14. H H
1500 m N’ 1500 m
16 23
D B A B
A 139
N
b 
1500 tan 67  N”
D
109
1500 tan 74
B

15. BD
 tan 74
1500 Similarly;
BD  1500 tan 74 AB  1500 tan 67 
NDB  DBN "  180 cointerior ' s  180, ND || N" B

16. BD
 tan 74
1500 Similarly;
BD  1500 tan 74 AB  1500 tan 67 
NDB  DBN "  180 cointerior ' s  180, ND || N" B
109  DBN "  180
DBN "  71

17. BD
 tan 74
1500 Similarly;
BD  1500 tan 74 AB  1500 tan 67 
NDB  DBN "  180 cointerior ' s  180, ND || N" B
109  DBN "  180
DBN "  71
Similarly;
ABN "  41

18. BD
 tan 74
1500 Similarly;
BD  1500 tan 74 AB  1500 tan 67 
NDB  DBN "  180 cointerior ' s  180, ND || N" B
109  DBN "  180
DBN "  71
Similarly;
ABN "  41
ABD  DBN "ABN " common ' s 
 ABD  30

19. H H
1500 m N’ 1500 m
16 23
D B A B
A 139
N
b 
1500 tan 67  N”
D
109 30
1500 tan 74
B

20. b 2  1500 2 tan 2 67   1500 2 tan 2 74  2 1500 tan 67  1500 tan 74 cos 30

21. b 2  1500 2 tan 2 67   1500 2 tan 2 74  2 1500 tan 67  1500 tan 74 cos 30
b  2798.96
 2799 (to nearest metre)
Anna and David are 2799 m apart.

22. H H
1500 m N’ 1500 m
16 23
D B A B
A 139
N
b 
1500 tan 67  N”
D
109 30
1500 tan 74
B

23. b 2  1500 2 tan 2 67   1500 2 tan 2 74  2 1500 tan 67  1500 tan 74 cos 30
b  2798.96
 2799 (to nearest metre)
Anna and David are 2799 m apart.
sin DAB sin 30


1500 tan 74 b

24. b 2  1500 2 tan 2 67   1500 2 tan 2 74  2 1500 tan 67  1500 tan 74 cos 30
b  2798.96
 2799 (to nearest metre)
Anna and David are 2799 m apart.
sin DAB sin 30


1500 tan 74 b
1500 tan 74 sin 30
sin DAB 
b
DAB  699' or 11051'

25. b 2  1500 2 tan 2 67   1500 2 tan 2 74  2 1500 tan 67  1500 tan 74 cos 30
b  2798.96
 2799 (to nearest metre)
Anna and David are 2799 m apart.
sin DAB sin 30


1500 tan 74 b
1500 tan 74 sin 30
sin DAB 
b
DAB  699' or 11051'
If DAB  699'
then BDA  8051'

26. b 2  1500 2 tan 2 67   1500 2 tan 2 74  2 1500 tan 67  1500 tan 74 cos 30
b  2798.96
 2799 (to nearest metre)
Anna and David are 2799 m apart.
sin DAB sin 30


1500 tan 74 b
1500 tan 74 sin 30
sin DAB 
b
DAB  699' or 11051'
If DAB  699'
then BDA  8051'
But DAB  BDA
 BDA  11051'

27. H H
1500 m N’ 1500 m
16 23
D B A B
A 139
N
b 11051' 
1500 tan 67  N”
D
109 30
1500 tan 74
B

28. b 2  1500 2 tan 2 67   1500 2 tan 2 74  2 1500 tan 67  1500 tan 74 cos 30
b  2798.96
 2799 (to nearest metre)
Anna and David are 2799 m apart.
sin DAB sin 30


1500 tan 74 b
1500 tan 74 sin 30
sin DAB 
b
DAB  699' or 11051'
If DAB  699'
then BDA  8051'
But DAB  BDA
 BDA  110 51' 
 The bearing of David from Anna is 24951'

29. 2000 Extension 1 HSC Q3c)
A surveyor stands at point A, which is due south of a tower OT of

height h m. The angle of elevation of the top of the tower from A is 45
The surveyor then walks 100 m due east to point B, from where she
measures the angle of elevation of the top of the tower to be 30

30. (i) Express the length of OB in terms of h.
T
h
30
0 B

31. (i) Express the length of OB in terms of h.
T
h
30
0 B
OB
 tan 60
h
OB  h tan 60

32. (i) Express the length of OB in terms of h.
T
h
30
0 B
OB
 tan 60
h
OB  h tan 60
(ii) Show that h  50 2

33. (i) Express the length of OB in terms of h.
T
h
30
0 B
OB
 tan 60
h
OB  h tan 60
(ii) Show that h  50 2
T
h
A 45 0

34. (i) Express the length of OB in terms of h.
T
h
30
0 B
OB
 tan 60
h
OB  h tan 60
(ii) Show that h  50 2
T
h
A 45 0
ATO is isosceles
 AO  h

35. (i) Express the length of OB in terms of h.
T
h
30
0 B
OB
 tan 60
h
OB  h tan 60
(ii) Show that h  50 2
T O
h h tan 60
h
A 45 0 A B
100
ATO is isosceles
 AO  h

36. (i) Express the length of OB in terms of h.
T
h
30
0 B
OB
 tan 60
h
OB  h tan 60
(ii) Show that h  50 2
T O h 2  100 2  h 2 tan 2 60
h h tan 60
h
A 45 0 A B
100
ATO is isosceles
 AO  h

37. (i) Express the length of OB in terms of h.
T
h
30
0 B
OB
 tan 60
h
OB  h tan 60
(ii) Show that h  50 2
T O h 2  100 2  h 2 tan 2 60
h h tan 60 h 2  100 2  3h 2
h
45  2h 2  100 2
A 0 A B 100 2
100 h2 
ATO is isosceles 2
100
 AO  h h
2
h  50 2

38. (iii) Calculate the bearing of B from the base of the tower.

39. (iii) Calculate the bearing of B from the base of the tower.
N
O
50 2
A 100 B

40. (iii) Calculate the bearing of B from the base of the tower.
N
100
tan AOB 
50 2
O
50 2
A 100 B

41. (iii) Calculate the bearing of B from the base of the tower.
N
100
tan AOB 
50 2
AOB  54 44'
O
50 2
A 100 B

42. (iii) Calculate the bearing of B from the base of the tower.
N
100
tan AOB 
50 2
AOB  54 44'
O
 bearing  180  54 44'
50 2  12516'
A 100 B

43. (iii) Calculate the bearing of B from the base of the tower.
N
100
tan AOB 
50 2
AOB  54 44'
O
 bearing  180  54 44'
50 2  12516'
A 100 B
Book 2: Exercise 2G odds
Exercise 2H evens